تعریف قطر چیست؟ | قطر در اشکال هندسی + فرمول ها

قطر یک مفهوم هندسی است که در بسیاری از انواع اشکال هندسی یافت می‌شود و در محاسبه محیط و مساحت آن‌ها به‌کار می‌آید. در ریاضی، قطر به‌صورت پاره‌خطی تعریف می‌شود که یک گوشه (رأس) چندضلعی را به گوشه دیگر غیرمجاور آن متصل می‌کند. اگر می‌خواهید بدانید تعریف قطر چیست و در هر کدام از اشکال هندسی دوبعدی و سه‌بعدی چند قطر وجود دارد، با این آموزش همراه باشید. 

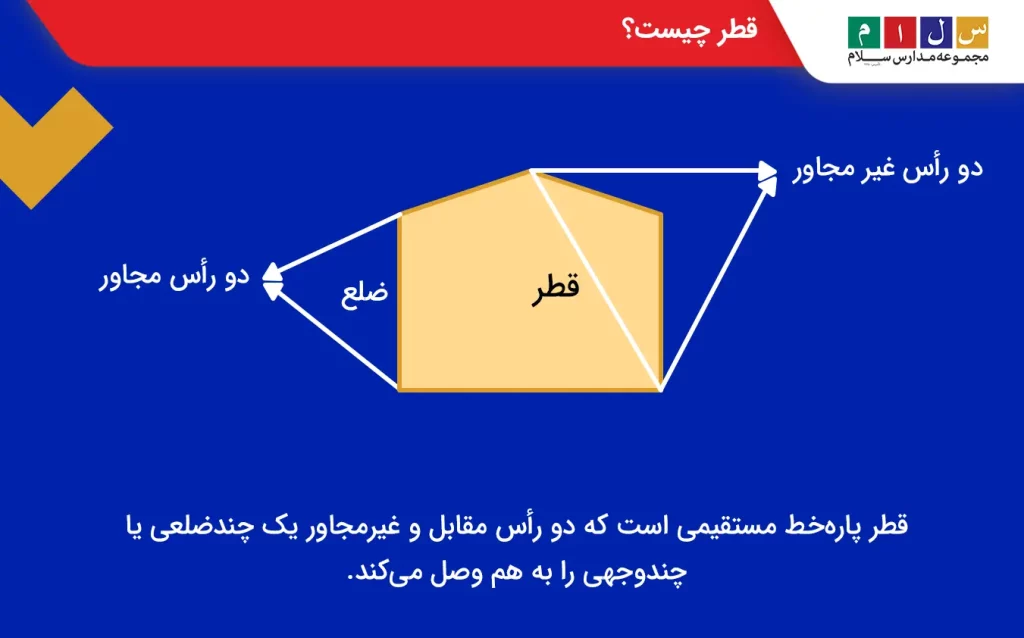
قطر چیست؟

برای تعریف قطر باید بگوییم که قطر پاره‌خط مستقیمی است که دو رأس مقابل و غیرمجاور یک چندضلعی یا چندوجهی را به هم وصل می‌کند.

البته، قطر در اشکال هندسی منحنی‌شکل که چندضلعی نیستند مانند دایره و بیضی هم وجود دارد، اما به‌گونه‌ای دیگر تعریف می‌شود. در بخش‌های بعدی، بیشتر دراین‌باره صحبت خواهیم کرد.

کاربرد قطر چیست؟

قطر به‌عنوان یک پاره‌خط در محاسبات مربوط به محیط، مساحت و ضلع اشکال هندسی دوبعدی و یافتن اندازه یال، مساحت و حجم اشکال سه‌بعدی بسیار مورد استفاده قرار می‌گیرد. 

ویژگی های قطر

قطر در اشکال هندسی گوناگون ویژگی‌های متفاوتی دارد. برای مثال، در مربع و لوزی، قطرها بر هم عمودند و همدیگر را نصف می‌کنند، درحالی که در چهارضلعی‌هایی مانند متوازی‌الاضلاع مستطیل و ذوزنقه قطرها بر هم عمود نیستند. حتی در اشکال سه‌بعدی نیز بسته به شکل موردنظر قطرها خصوصیات متفاوتی دارند که در ادامه مقاله در این مورد بیشتر توضیح خواهیم داد.

تفاوت ضلع و قطر چند ضلعی چیست؟

در یک چندضلعی، ضلع به پاره‌خطی گفته می‌شود که دو رأس مجاور را به هم وصل می‌کند، اما منظور از قطر پاره‌خطی است که دو رأس غیرمجاور را به یکدیگر متصل می‌کند.

قطر اشکال هندسی دوبعدی

در این بخش، بررسی می‌کنیم که در اشکال دوبعدی شناخته‌شده قطر چیست و چند قطر دارند.

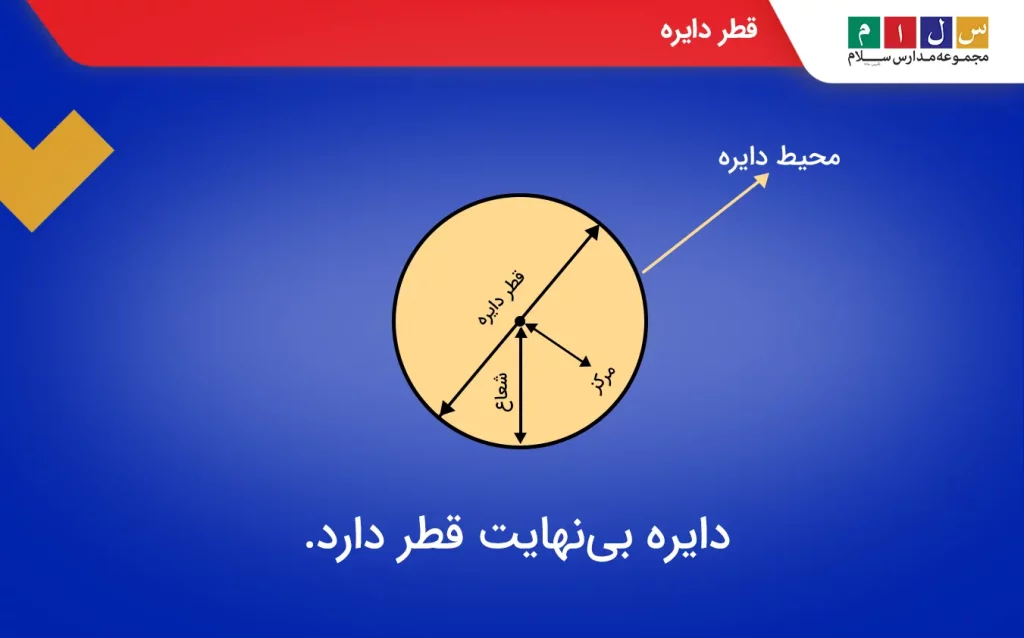
قطر دایره

قطر یک دایره، پاره‌خطی است که از مرکز آن می‌گذرد و دو نقطه از دایره را که روی محیط و مقابل هم قرار دارند به هم متصل می‌کند. شعاع دایره همان نصف قطر است. از آنجا که محیط یک دایره از بی‌نهایت نقطه تشکیل شده است، می‌توان گفت یک دایره بی‌نهایت قطر دارد.

اندازه قطر یک دایره دو برابر شعاع آن است. بنابراین، با استفاده از قطر می‌توان مساحت دایره و محیط دایره را محاسبه کرد. همچنین، اگر مقدار محیط یا مساحت یک دایره را داشته باشیم، به‌راحتی می‌توانیم طول قطر یک دایره را تعیین کنیم.

فرمول تعیین قطر دایره برحسب شعاع، محیط و مساحت دایره به‌صورت زیر است:

• فرمول محاسبه قطر با شعاع:

• فرمول محاسبه قطر برحسب محیط دایره:

۳/۱۴ ÷  محیط دایره = قطر

• فرمول محاسبه قطر برحسب مساحت دایره:

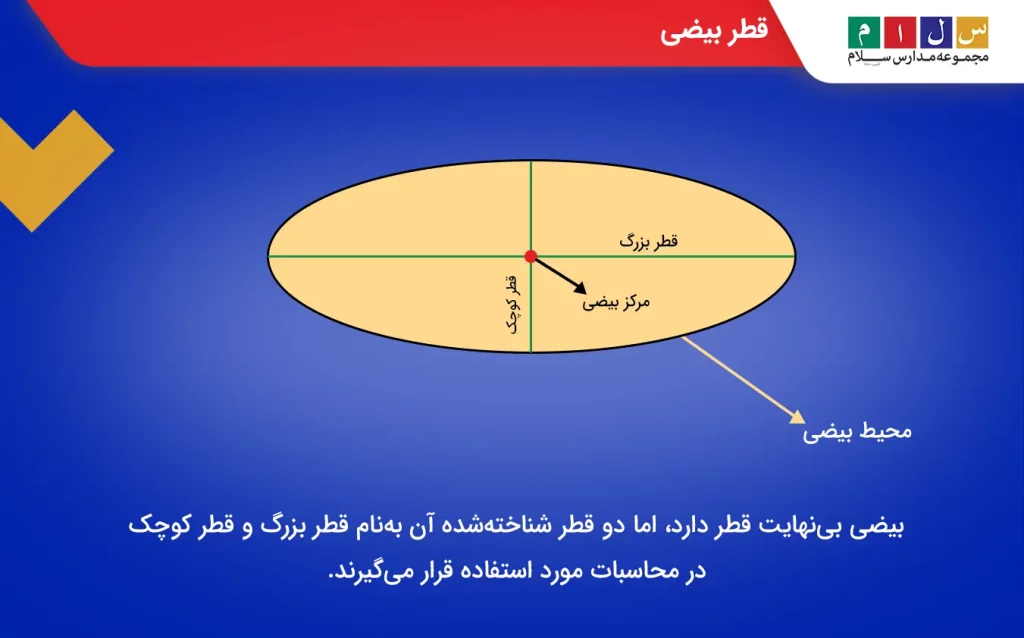
قطر بیضی

قطر بیضی پاره‌خطی است که نقاط مقابل روی محیط بیضی را به هم وصل می‌کند. یک بیضی می‌تواند بی‌نهایت قطر داشته باشد. دو تا از قطرهای بیضی که در محاسبه محیط و مساحت این شکل هندسی مورد استفاده قرار می‌گیرند، قطر بزرگ و کوچک نام دارند.

قطر مثلث

مثلث یک شکل هندسی دوبعدی با سه ضلع و سه رأس است. در این شکل هندسی، هیچ دو رأس غیرمجاوری وجود ندارد. به همین دلیل، نمی‌توان برای آن قطر رسم کرد. بنابراین مثلث قطر ندارد.

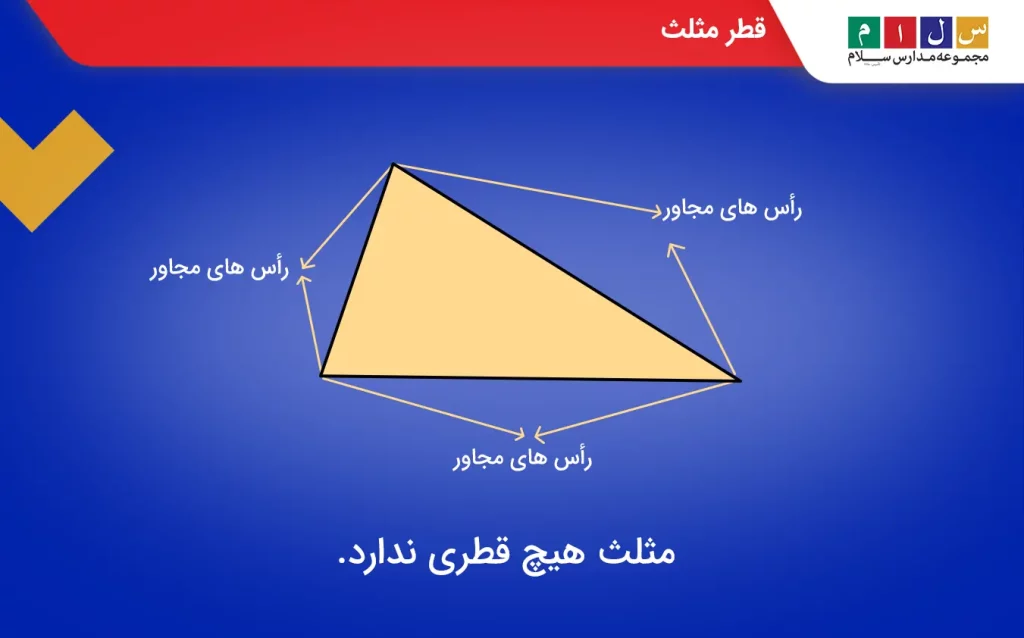
پیشنهاد مطالعه: مساحت مثلث چیست؟

قطر مربع

مربع یک چهارضلعی با چهار ضلع برابر و چهار رأس ۹۰ درجه است که ۲ قطر دارد. قطرهای مربع با هم برابرند و علاوه‌بر اینکه همدیگر را نصف می‌کنند بر یکدیگر عمود هم هستند. این یعنی اینکه قطرهای مربع عمودمنصف یکدیگرند.

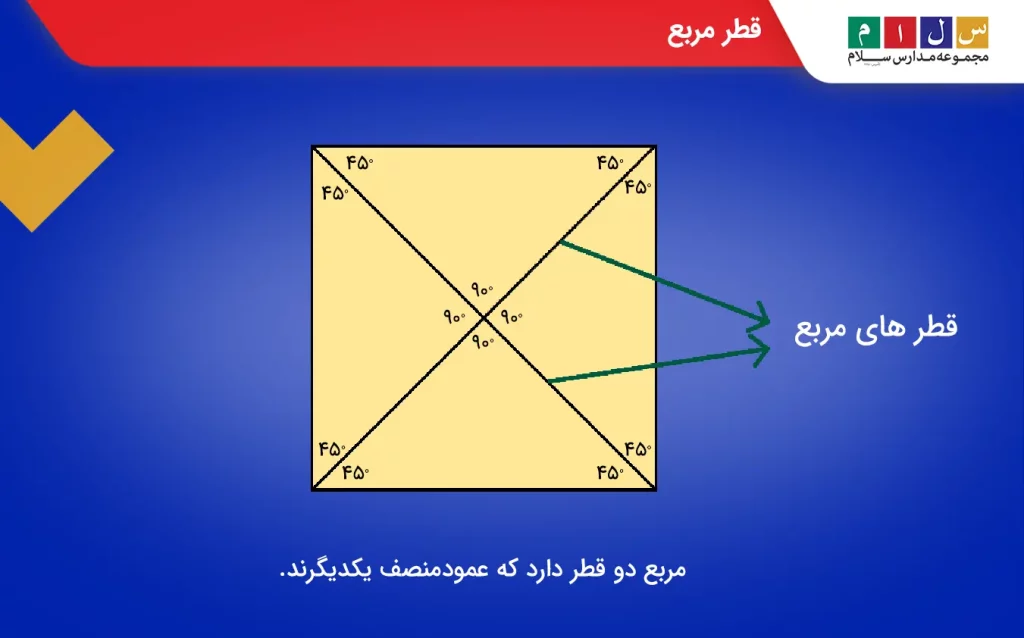
قطرها زاویه‌های قائمه مربع را به دو زاویه برابر ۴۵ درجه‌ای تقسیم می‌کنند. از آنجا که مربع توسط هر کدام از قطرها به دو مثلث قائم‌الزاویه مساوی تقسیم می‌شود، می‌توانیم با داشتن مقدار ضلع مربع، اندازه قطر را با کمک قضیه فیثاغورس محاسبه کنیم. به‌طور کلی، اگر طول یک ضلع مربع برابر با a باشد، اندازه قطر آن از رابطه زیر محاسبه خواهد شد:

• a: ضلع مربع
• d: قطر مربع

با توجه به اینکه قطر و ضلع مربع با هم رابطه مستقیمی دارند، می‌توانیم با داشتن مقدار قطر مربع، محیط و مساحت آن را حساب کنیم.

پیشنهاد مطالعه: مساحت مربع

مثال: اندازه قطر مربعی به‌ ضلع ۷ سانتی‌متر را به‌دست آورید.

جواب: با توجه به فرمول قطر مربع داریم:

$$d=\sqrt{۲}a$$

محاسبه مساحت مربع با قطر چگونه است؟

می‌دانیم که مساحت مربع از فرمول «اندازه یک ضلع ضربدر خودش» محاسبه می‌شود یعنی اگر ضلع مربع را با a نشان دهیم، خواهیم داشت:

A=√a^۲

با توجه به رابطه ضلع و قطر مربع، داریم:

d=√۲a

قطر مستطیل

مستطیل یکی دیگر از چهارضلعی‌هاست که دارای چهار زاویه ۹۰ درجه است و اضلاع مقابل آن دوبه‌دو با هم مساوی هستند. مستطیل ۲ قطر برابر دارد که همدیگر را نصف می‌کنند، اما بر هم عمود نیستند.

هر کدام از قطرهای مستطیل را به دو مثلث قائم‌الزاویه یکسان تقسیم می‌کنند. ازاین‌رو، می‌توان طول قطر مستطیل را با استفاده از قضیه فیثاغورس تعیین کرد.

همان‌طور که می‌بینید، اندازه قطر مستطیل را می‌توانیم با استفاده از مقدار طول و عرض آن به‌دست آوریم. با توجه به رابطه‌ای که این سه پارامتر با هم دارند، می‌توان گفت با داشتن قطر و یکی از دو پارامتر طول یا عرض، محیط و مساحت مستطیل قابل محاسبه است.

محاسبه محیط و مساحت مستطیل با قطر چگونه است؟

محیط مستطیل از «مجموع طول و عرض ضربدر دو» به‌دست می‌آید و مساحت آن نیز از فرمول «طول ضربدر عرض» تعیین می‌شود. اگر اندازه قطر و یکی از اضلاع مستطیل (طول یا عرض) را داشته باشیم، فرمول محیط مستطیل برحسب قطر به‌صورت زیر خواهد بود:

• A: مساحت مستطیل
• x: اندازه طول یا عرض
• d: قطر مستطیل

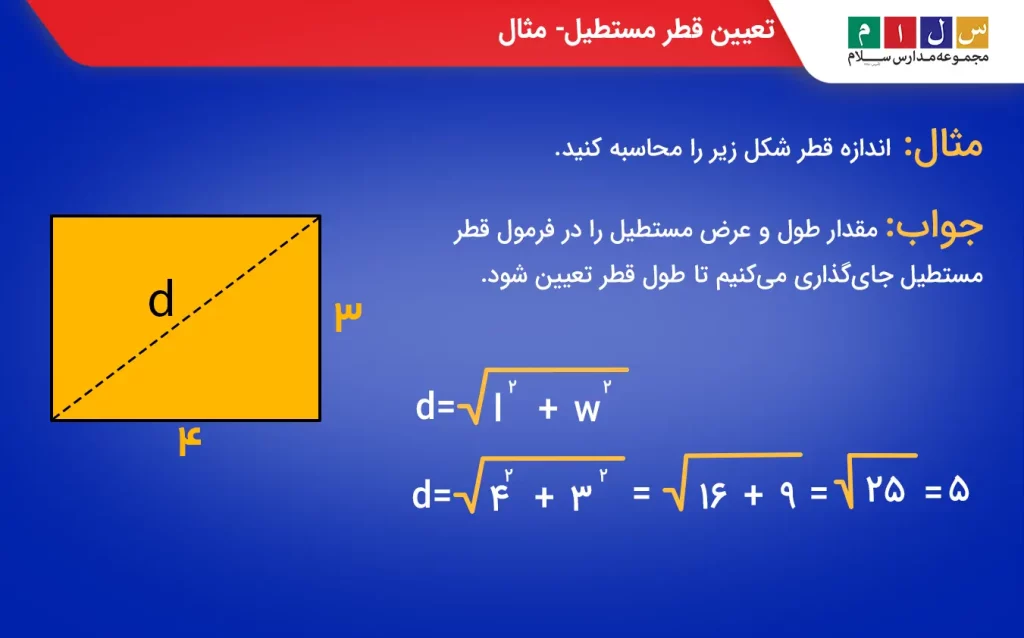
قطر لوزی

لوزی یک چهارضلعی با چهار ضلع برابر است که در آن زاویه‌های مقابل با هم برابرند. لوزی ۲ قطر نابرابر دارد که بر هم عمود هستند و با نام قطر بزرگ و قطر کوچک شناخته می‌شوند. قطرها زاویه‌های لوزی را به دو قسمت مساوی تقسیم می‌کنند. بنابراین، می‌توان گفت قطرهای لوزی نیمسازهای زوایای آن نیز هستند.

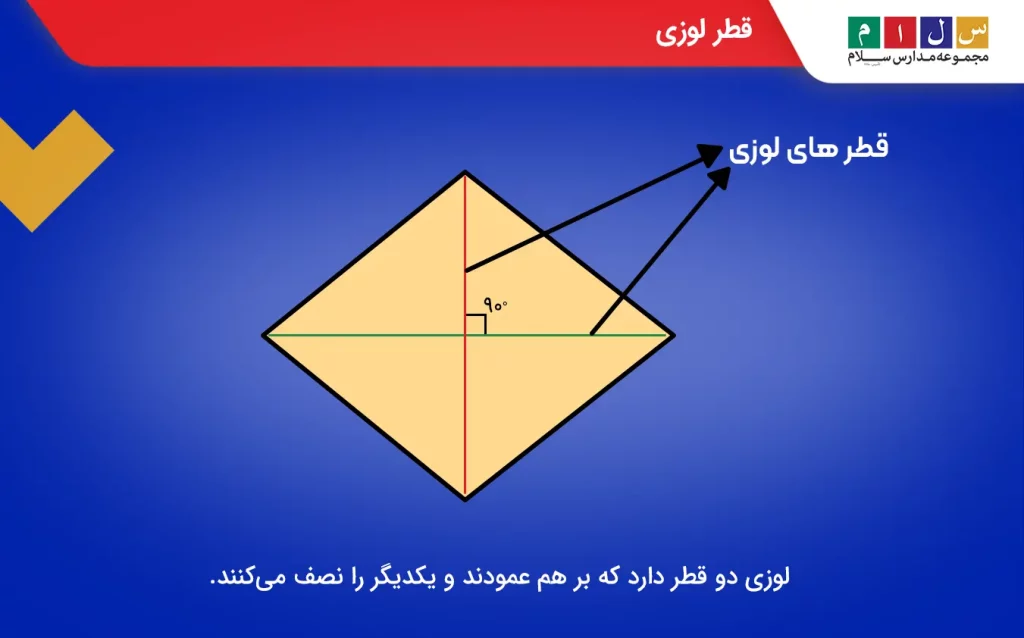
از آنجا که قطرهای لوزی بر هم عمودند، می‌توان با استفاده از قضیه فیثاغورس، فرمول مقدار ضلع لوزی را برحسب قطرهای آن به‌صورت زیر تعیین کرد:

 پس علاوه‌بر مساحت لوزی می‌توانیم مقدار محیط لوزی را نیز که از فرمول «ضلع لوزی × ۴» به‌دست می‌آید، با کمک قطرها محاسبه کنیم.

قطر متوازی الاضلاع

متوازی‌الاضلاع چهار رأس و چهار ضلع دارد. در متوازی‌الاضلاع، اضلاع روبه‌رو و زوایای مقابل با هم برابرند. این چهارضلعی دارای ۲ قطر است که همدیگر را نصف می‌کنند.

اندازه قطرهای متوازی‌الاضلاع را می‌توانیم با داشتن دو ضلع و زوایای آن به‌دست آوریم. گاهی اوقات می‌توان برای محاسبه محیط و مساحت متوازی الاضلاع از قطرها نیز استفاده کرد.

اندازه قطر و مساحت متوازی الاضلاع بر اساس آن

اندازه قطرهای یک متوازی‌الاضلاع از فرمول‌های زیر محاسبه می‌شود:

• p و q: قطرهای متوازی‌الاضلاع
• x و y: اضلاع متوازی‌الاضلاع
• A و B: زاویه‌های داخلی متوازی‌الاضلاع

مساحت متوازی‌الاضلاع را می‌توان با استفاده از قطرها و زوایای بین آن‌ها به‌دست آورد. این فرمول‌ها عبارت‌اند از:

• p و q: قطرهای متوازی‌الاضلاع
• x و y: زوایای بین قطرهای متوازی‌الاضلاع
• A: مساحت متوازی‌الاضلاع

جدول ویژگی های قطر در اشکال هندسی مختلف

در جدول زیر تعداد قطر در اشکال هندسی مختلف را همراه با ویژگی‌های آن‌ها بیان کرده‌ایم.

شکل	تعداد قطر	ویژگی قطرها
	۲	قطرها برابر و عمودمنصف یکدیگرند و نیمساز زوایای داخلی مربع و خط تقارن آن نیز محسوب می‌شوند.
	۲	قطرها با هم برابرند و همدیگر را نصف می‌کنند.
	۲	از میان انواع ذوزنقه تنها در ذوزنقه متساوی‌الساقین طول قطرها با هم برابر است.
	۲	قطرها عمودمنصف یکدیگرند و نیمساز زوایای داخلی لوزی و خط تقارن آن نیز محسوب می‌شوند.
	۲	قطرها همدیگر را نصف می‌کنند.
	ندارد	هیچ‌کدام از انواع مثلث قطر ندارند.
	بی‌شمار	طول قطرها با هم برابر است و  در مرکز دایره همدیگر را نصف می‌کنند. قطرهای دایره خط تقارن آن نیز هستند.
	بی‌شمار	مهم‌ترین قطرهای بیضی قطر بزرگ و کوچک آن است که عمودمنصف یکدیگر هستند و خط تقارن بیضی نیز به‌شمار می‌روند.

جدول قطر در چند وجهی ها

در این بخش، فرمول قطرهای دو نوع از چندوجهی‌های شناخته‌شده به‌نام مکعب مربع و مستطیل را در جدول زیر آورده‌ایم.

شکل	فرمول قطر وجه	فرمول قطر درون حجم
	2a√	3a√

قطر ذوزنقه

ذوزنقه یکی دیگر از انواع چهارضلعی است که دو ضلع موازی و دو ضلع غیرموازی دارد و مانند سایر چهارضلعی‌ها دارای ۲ قطر است. در ذوزنقه متساوی‌الساقین که دو ساق آن با هم برابر است، طول قطرها یکسان است.

فرمول تعداد قطر در یک چندضلعی

تعداد قطرهای یک چندضلعی را می‌توان از فرمول زیر به‌دست آورد:

۲÷ (۳ – تعداد اضلاع) × تعداد اضلاع) = تعداد قطر

این فرمول نشان می‌دهد که برای محاسبه تعداد قطرهای یک چندضلعی کافی‌ست تعداد اضلاع آن را بدانیم. برای مثال، در یک پنج‌ضلعی تعداد اضلاع (n) برابر با ۵ است و از این‌ رو، تعداد قطرهای آن به‌صورت زیر محاسبه می‌شود:

$$d_n=\frac{n(n-<!--\; -\; -->۳)}{۲}=\frac{۵(۵-<!--\; -\; -->۳)}{۲}=\frac{۵}{۲}=۵$$

اگر تعداد اضلاع را ۳ قرار دهیم، تعداد قطرها صفر می‌شود، یعنی همان چیزی که قبلاً هم درمورد مثلث گفتیم. همچنین، اگر تعداد ضلع‌ها یعنی n را ۴ قرار دهیم، تعداد قطرها برابر با ۲ خواهد بود. بنابراین، در تمام چهارضلعی‌ها ۲ قطر خواهیم داشت. 

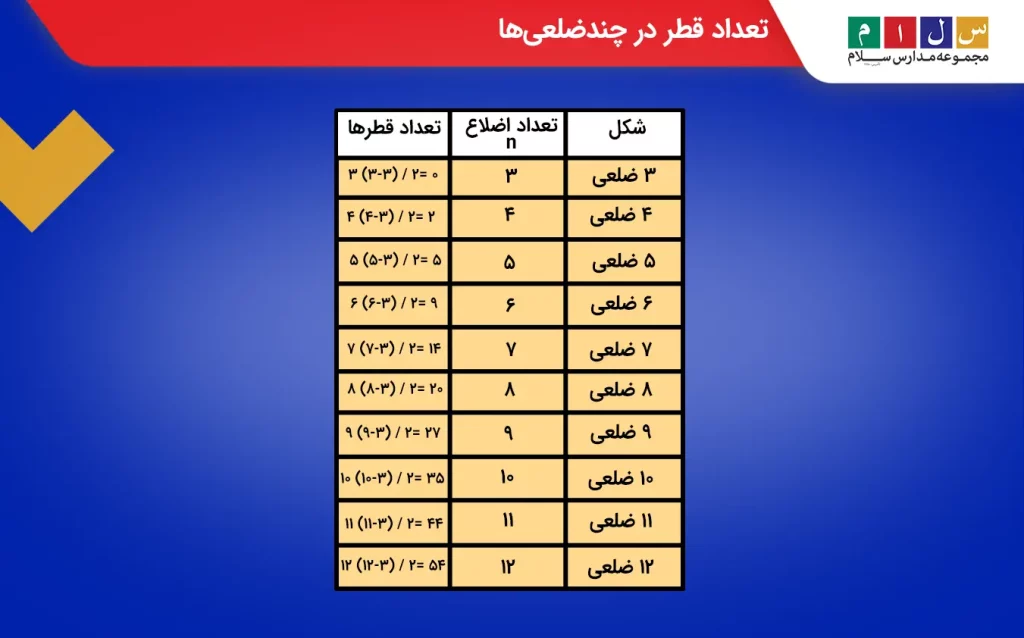
در جدول زیر، تعداد قطرهای چندضلعی‌های گوناگون آورده شده است.

قطر اشکال هندسی سه بعدی

اشکال هندسی سه‌بعدی مانند اشکال دوبعدی می‌توانند قطر داشته باشند. درادامه، قطرهای چند نمونه از اشکال سه‌بعدی را  بررسی می‌کنیم.

قطر مکعب

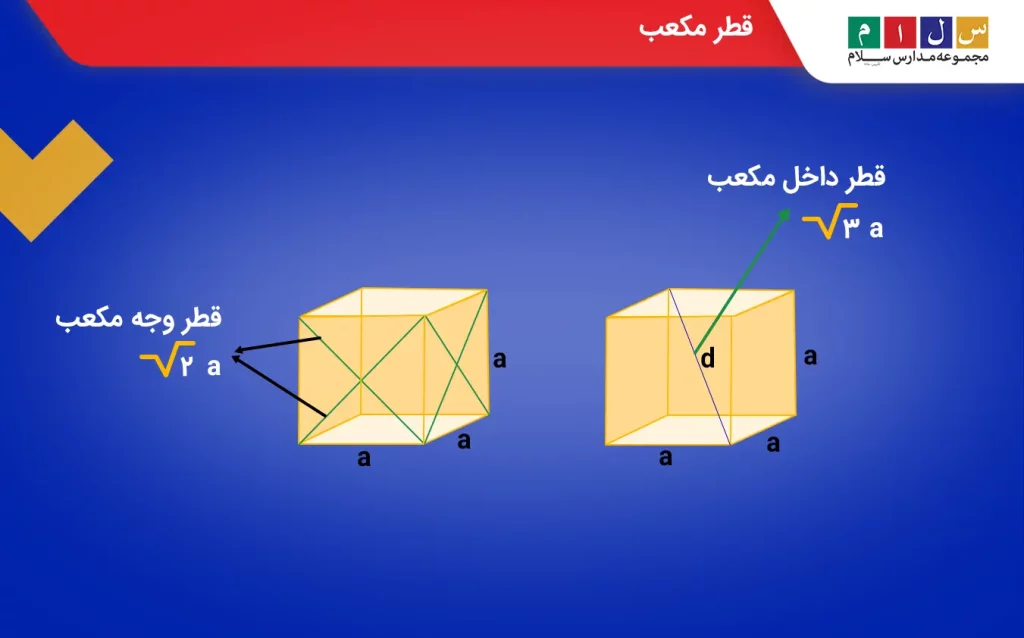
یک مکعب مربع را که ۶ وجه مربعی به ضلع a دارد در نظر بگیرید. در هر کدام وجه‌ها می‌توان مانند شکل زیر دو قطر رسم کرد که طول آن‌ها برابر با 2a√ است. این مکعب علاوه‌بر قطر وجه‌ها، قطرهای دیگری هم دارد که در داخل آن قرار می‌گیرند و یک رأس را به رأس غیرمجاور خود در وجه دیگر متصل می‌کنند. طول این قطرها برابر است با 3a√.

قطر مکعب مستطیل

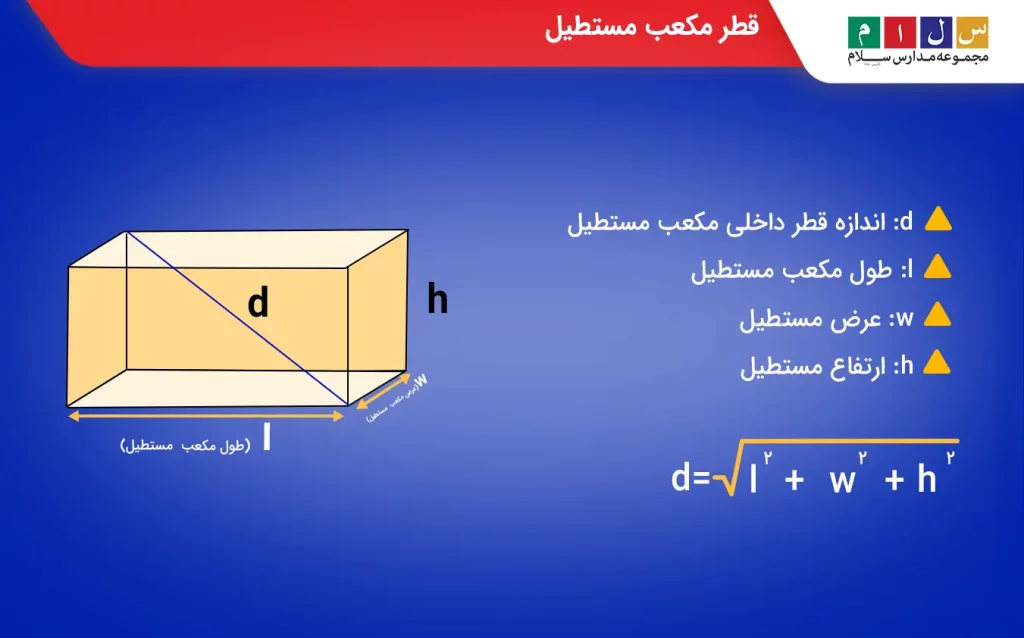
مکعب مستطیل دارای ۶ وجه مستطیلی است و مانند مکعب مربع دو نوع قطر دارد: قطر روی وجه و قطر درون مکعب مستطیل. از آنجا که مقدار طول، عرض و ارتفاع مکعب مستطیل متفاوت است، طول قطر هر کدام از وجه‌ها را می‌توان با کمک قضیه فیثاغورس محاسبه کرد. اندازه قطر داخلی مکعب مستطیل را هم می‌توان از فرمول زیر به‌دست آورد:

قطر کره زمین

حداکثر فاصله مستقیم از یک سمت کره تا سمت دیگر آن را قطر کره می‌گویند. یک کره بی‌نهایت قطر دارد که در محاسبات مربوط به محیط و مساحت کره مورد استفاده قرار می‌گیرد. کره زمین نیز که تقریباً کروی‌شکل است، دارای قطری با اندازه مشخص است. قطر کره زمین تقریباً برابر است با ۱۲۷۵۶ کیلومتر.

پیشنهاد مطالعه: وتر چیست؟

سخن پایانی

قطر یکی از مشخصه‌های اشکال هندسی است که در محاسبه محیط و مساحت آن‌ها مورد استفاده قرار می‌گیرد. به‌طور کلی، قطر پاره‌خطی است که رأس‌های غیرمجاور را در یک چندضلعی یا چندوجهی به هم متصل می‌کند. در اشکال دوبعدی بسته به نوع شکل، فرمول محاسبه اندازه قطر می‌تواند متفاوت باشد، اما تعداد قطر در یک چندضلعی را می‌توان تنها از فرمول ۲÷ (۳ – تعداد اضلاع) × تعداد اضلاع)  محاسبه کرد.

از میان چندضلعی‌ها، مثلث تنها شکلی است که قطر ندارد. در اشکال سه‌بعدی چندوجهی مانند مکعب مربع و مستطیل نیز قطر وجود دارد، اما این نوع اشکال دو نوع قطر دارند: قطر روی وجه‌ها و قطر داخل مکعب که رأس‌های غیرمجاور دو وجه را به هم وصل می‌کند.

سؤالات متداول

1. تعریف قطر چیست؟
   قطر پاره‌خطی است که دو رأس غیرمجاور یک چندضلعی یا چندوجهی را به هم وصل می‌کند.
2. تعداد قطر در یک چندضلعی چگونه به‌دست می‌آید؟
   تعداد قطر در یک چندضلعی با n ضلع، از رابطه ۲÷ (۳ – تعداد اضلاع) × تعداد اضلاع)  به‌دست می‌آید.
3. مثلث چند قطر دارد؟
   مثلث هیچ قطری ندارد.
4. چهارضلعی‌ها چند قطر دارند؟
   چهارضلعی‌ها ۲ قطر دارند.
5. دایره چند قطر دارد؟
   دایره بی‌نهایت قطر دارد.
6. قطر کره زمین چقدر است؟
   قطر کره زمین تقریباْ ۱۲۷۵۶ کیلومتر است.