زاویه ازجمله مفاهیم هندسی است که در محیط پیرامونمان و حتی لوازم منزل نمونه‌های آن را به‌وفور دیده‌ایم. گوشه اتاق یا میز و صندلی، عقربه‌های ساعت که به هم نزدیک یا از هم دور می‌شوند و حتی دری که باز و بسته می‌کنید، همگی نمونه‌هایی از مفهوم زاویه در محیط زندگی ما هستند. برای اینکه بیشتر با زاویه آشنا شوید، پیشنهاد میکنیم این آموزش را دنبال کنید تا هم بدانید زاویه چیست و چه انواعی دارد و هم روش تعیین اندازه زاویه‌های مختلف را در اشکال گوناگون بیاموزید.
پیشنهاد مطالعه: نیمساز زاویه چیست و چگونه رسم میشود؟
زاویه چیست؟
زاویه یا گوشه یکی از مفاهیم هندسی است که از برخورد دو نیمخط ساخته میشود. محل برخورد دو نیمخط (یا دو ضلع) زاویه را رأس زاویه میگویند. طبق این تعریف می‌توان گفت که هر زاویه شامل دو ضلع (نیمخط) و یک رأس است.
زاویه را معمولاً با حروف مختلف نام‌گذاری می‌کنند. برای مثال، زاویه نشان‌داده‌شده در شکل زیر را زاویه (آ ب ج) می‌خوانیم. این زاویه شامل دو نیمخط (آ ب) و (ب ج) و یک رأس (ب) است.
زاویه از برخورد دو نیمخط ساخته شده. محل برخورد دو نیمخط یا دو ضلع زاویه رأس زاویه است. برای آشنایی کامل با مفهوم خط و نیمخط پیشنهاد میکنیم نگاهی به مقاله تفاوت خط و نیم خط و پاره خط بیندازید.
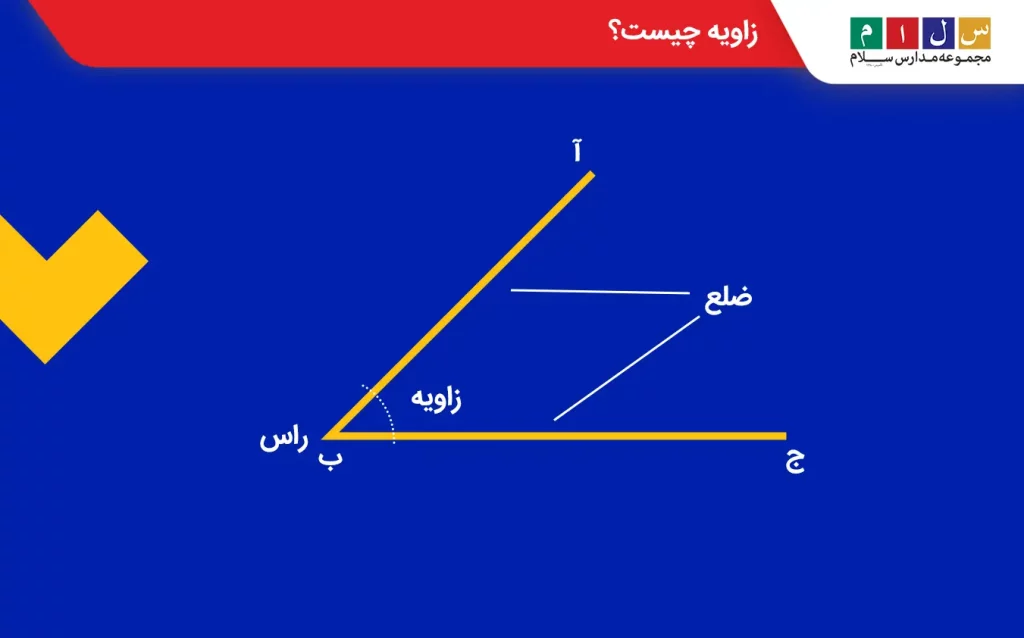
البته، می‌توان زاویه را با یک حرف نیز نام‌گذاری کرد. این حرف کنار رأس زاویه نوشته میشود. مثلاً زاویه زیر را زاویه (م) می‌خوانیم.
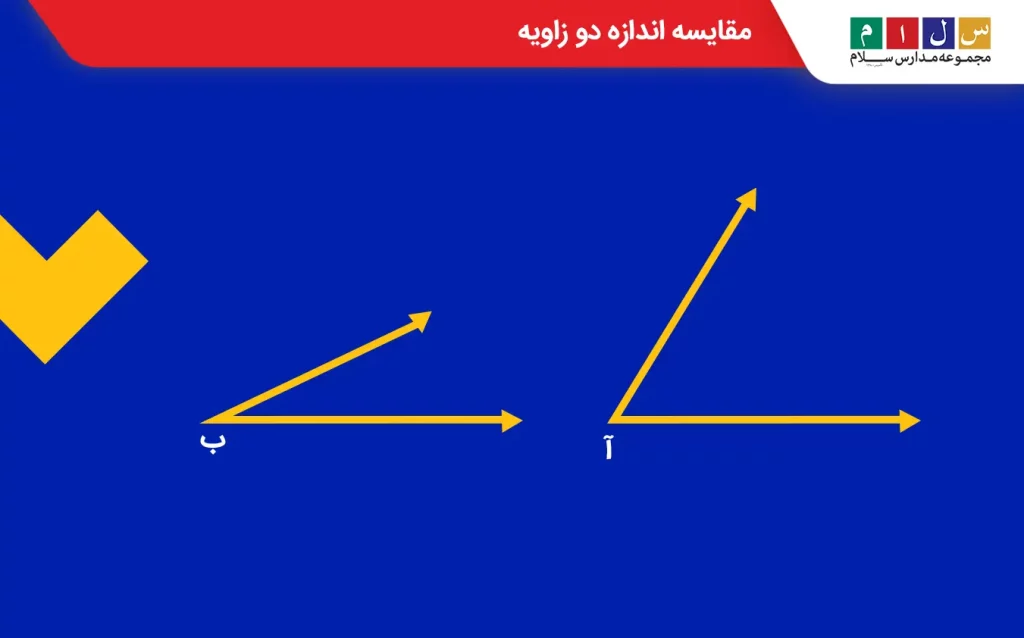
هر زاویهای اندازه‌ای دارد که با باز و بسته شدن دو نیمخط آن تغییر می‌کند و کم یا زیاد میشود. برای مثال، در شکل زیر مقدار بازشدگی زاویه (آ) از زاویه (ب) بیشتر است. درنتیجه می‌توان گفت که اندازه زاویه (آ) بزرگ‌تر از اندازه زاویه (ب) است.
پیشنهاد مطالعه: انجام راحت محاسبات با جمع و تفریق فرایندی
اولین نفری باشید که از اخبار و اطلاعیه‌های مرتبط با پایه تحصیلیتان باخبر میشود!
اندازه گیری زاویه
همان‌طور که گفتیم، اندازه زاویه یعنی مقدار باز شدن دو نیمخط یا دو ضلع زاویه نسبت به همدیگر. برای اندازه گیری زاویه از وسایلی مانند نقاله و گونیا استفاده میشود.
اندازه گیری زاویه با نقاله
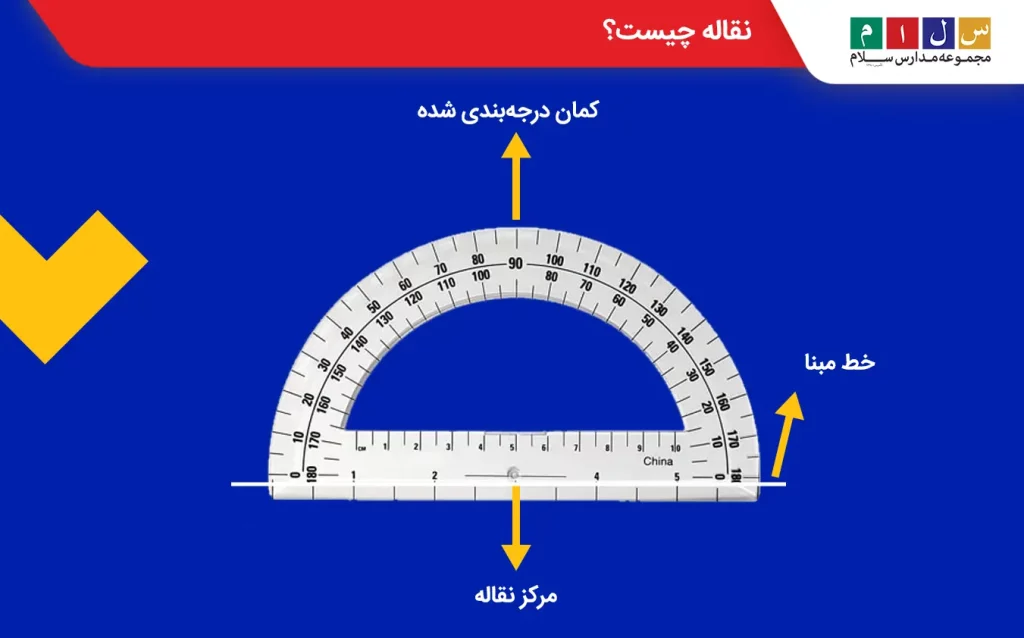
نقاله یک وسیله نیم‌دایره‌ای‌شکل است که برای اندازه‌گیری زاویه از آن استفاده میشود. نیم‌دایره نقاله به ۱۸۰ قسمت مساوی تقسیم شده است. به هر کدام از این قسمت‌ها «درجه» میگویند. درجه را با نماد ˚ نشان می‌دهند، مثلاً اگر اندازه زاویهای ۶۰ درجه باشد، می‌نویسیم ˚۶۰.
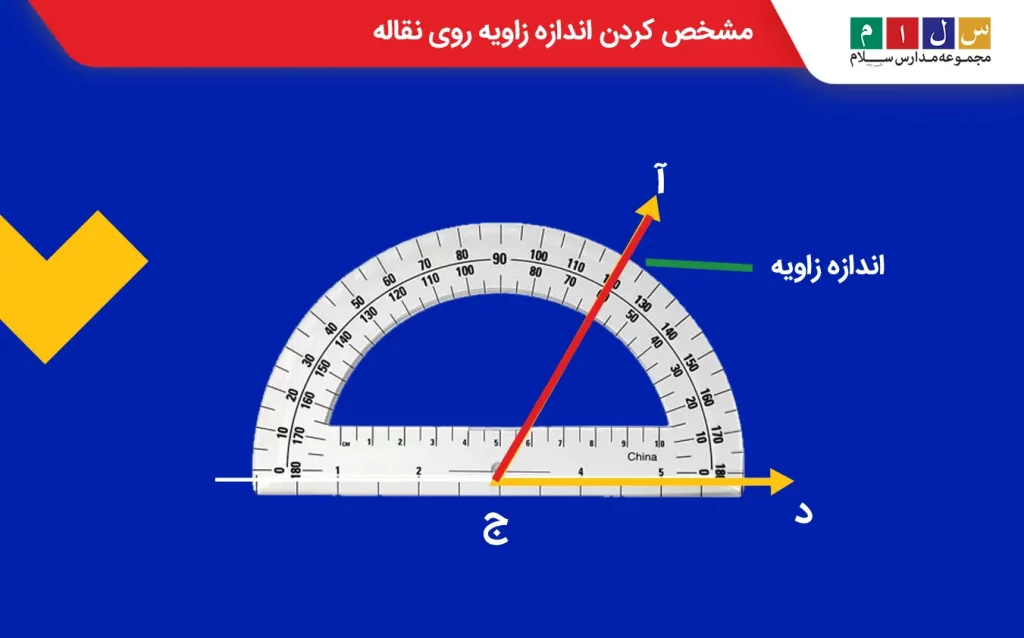
برای اندازه گرفتن زاویهای مانند زاویه (آ ج د) در شکل زیر باید مراحل زیر را انجام دهید:
مرحله اول: مرکز نقاله را روی رأس زاویه قرار دهید و خط مبنای نقاله (صفر نقاله) را روی یکی از ضلع‌های زاویه منطبق کنید.
مرحله دوم: عددی که ضلع دوم زاویه بر آن منطبق است، اندازه زاویه را به شما نشان میدهد. مثلاً در شکل زیر، ضلع دوم زاویه روی عدد ۶۰ قرار گرفته و نشان میدهد که اندازه زاویه «آ ج د» ۶۰ درجه است.
علاوه‌بر نقاله، با گونیا هم می‌توانید برخی از زاویه‌ها را اندازه بگیرید یا حتی بسازید.
انواع زاویه کدام اند؟
زاویه را براساس میزان بازشدگی و محل قرار گرفتنشان در اشکال مختلف به چند نوع تقسیم‌بندی می‌کنند که درادامه هر کدام را همراه با شکل توضیح میدهیم.
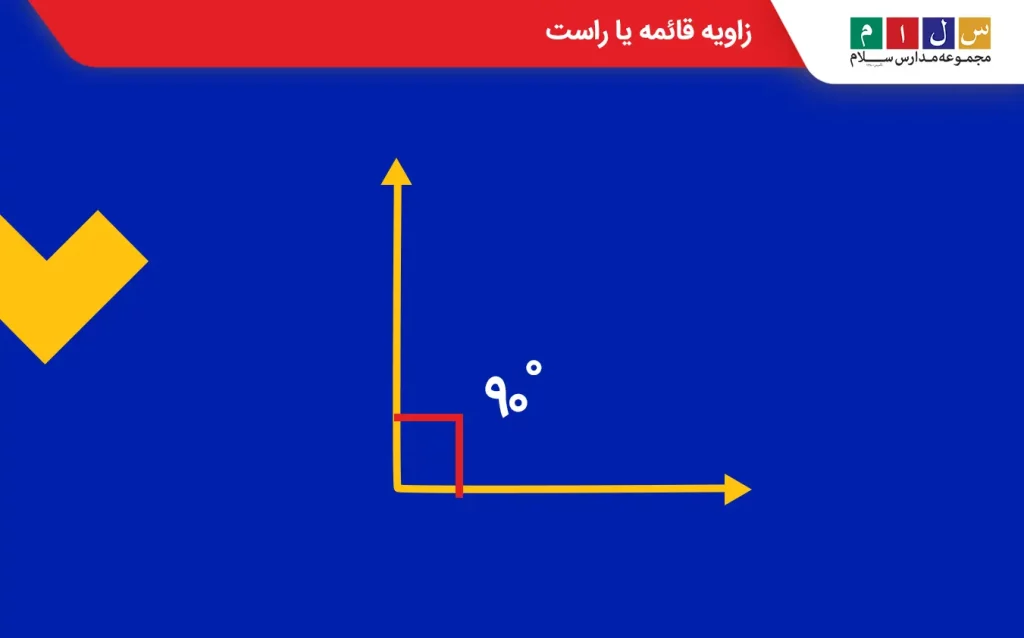
زاویه راست یا قائمه
زاویهای که اندازه آن ۹۰ درجه باشد را زاویه قائمه یا راست می‌نامند. گونیا به‌دلیل داشتن یک زاویه ۹۰ درجه ابزار مناسبی برای رسم و اندازه‌گیری این نوع زاویه است. زاویه راست را با یک مربع کوچک در رأس آن نشان می‌دهند.
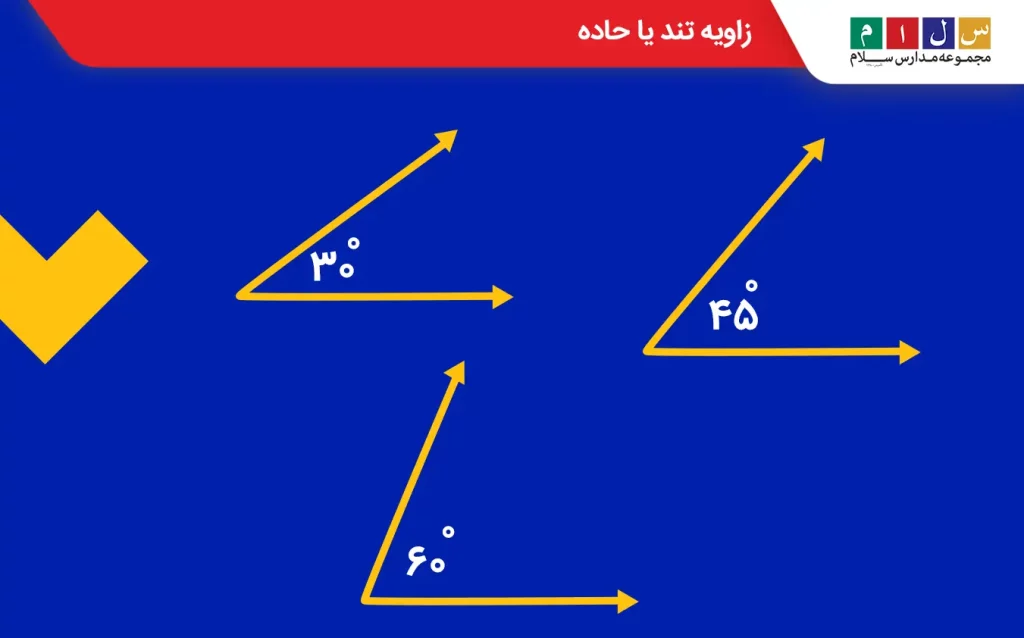
زاویه تند یا حاده
اگر اندازه زاویه بین صفر تا ۹۰ درجه باشد، یعنی از زاویه راست کوچک‌تر باشد، زاویه ما تند یا حاده خواهد بود.
زاویه تند یا حاده زاویهای است که اندازه آن کمتر از ۹۰ درجه است
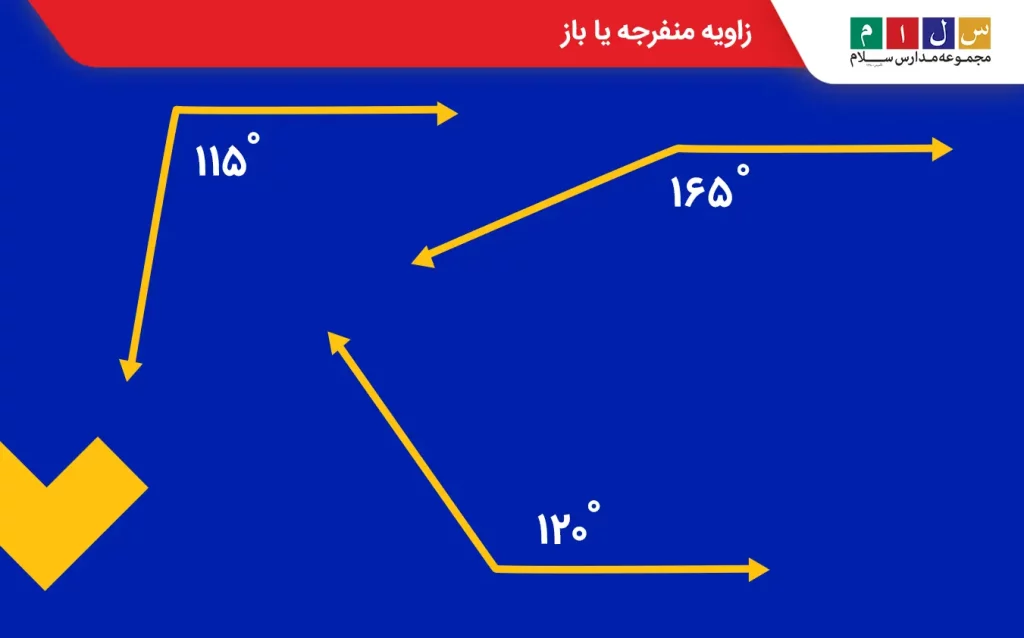
زاویه باز یا منفرجه
زاویه باز یا منفرجه زاویهای است که از زاویه راست بزرگ‌تر و اندازه آن بین ۹۰ تا ۱۸۰ درجه باشد.
زاویه نیم صفحه
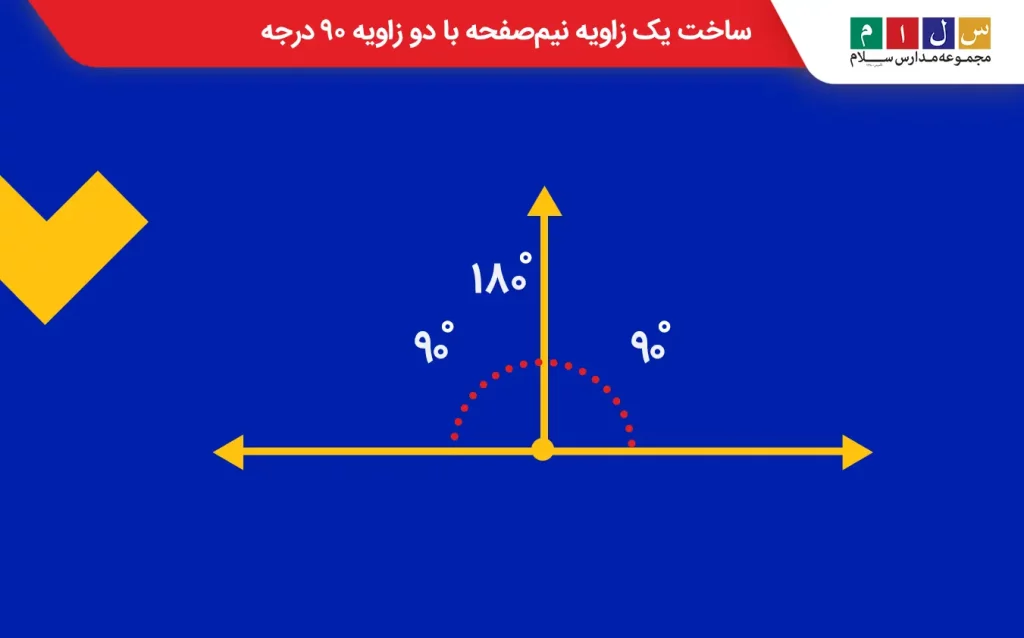
زاویه ۱۸۰ درجه را زاویه نیمصفحه میگویند. این زاویه مانند یک خط راست به‌نظر می‌رسد و دو ضلع آن خلاف جهت هم قرار دارند.
اگر دو زاویه راست را مانند شکل زیر کنار هم قرار دهید یک زاویه نیمصفحه ساخته میشود.
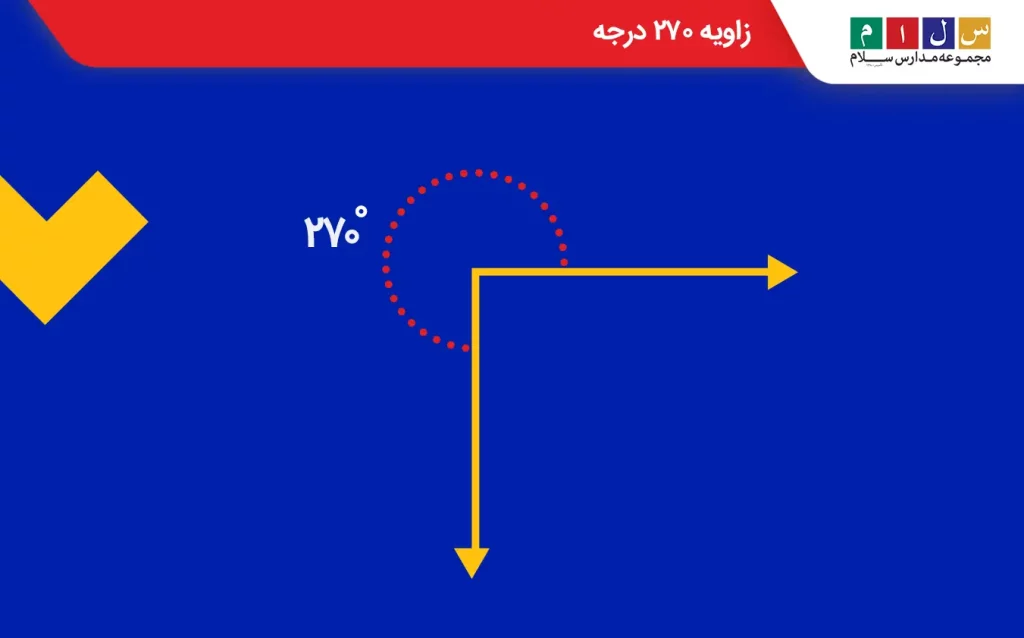
زاویه ۲۷۰ درجه
زاویه ۲۷۰ درجه از سه زاویه ۹۰ درجه ساخته شده است.
زاویه تمام صفحه
زاویه ۳۶۰ درجه را زاویه تمامصفحه یا زاویه کامل میگویند. این زاویه از چهار زاویه ۹۰ درجه ساخته شده است.
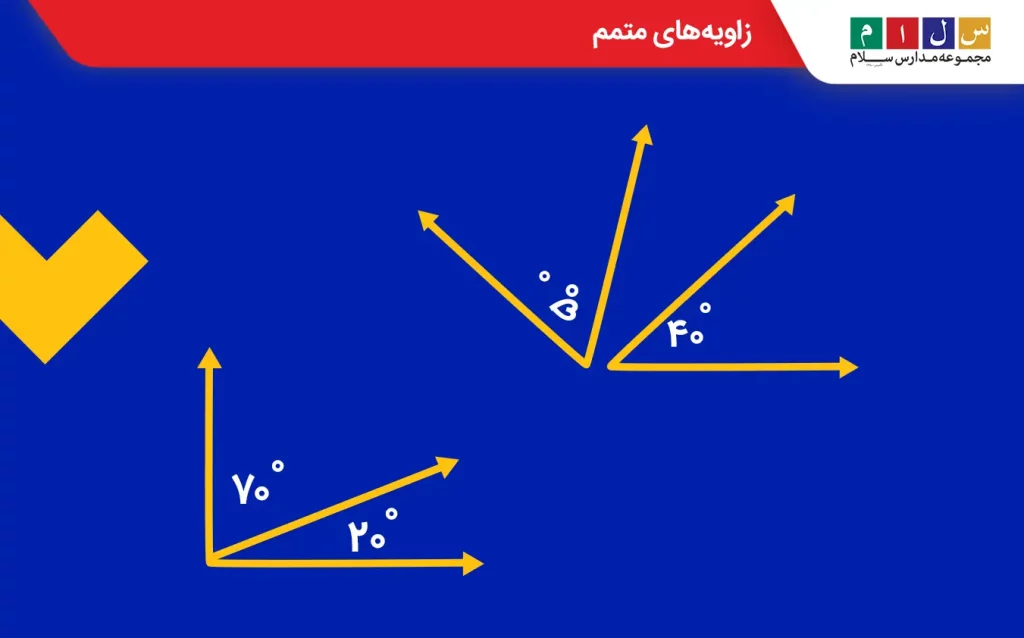
زاویه متمم
اگر مجموع دو زاویه برابر با ۹۰ درجه باشد، آن دو زاویه را متمم میگویند.
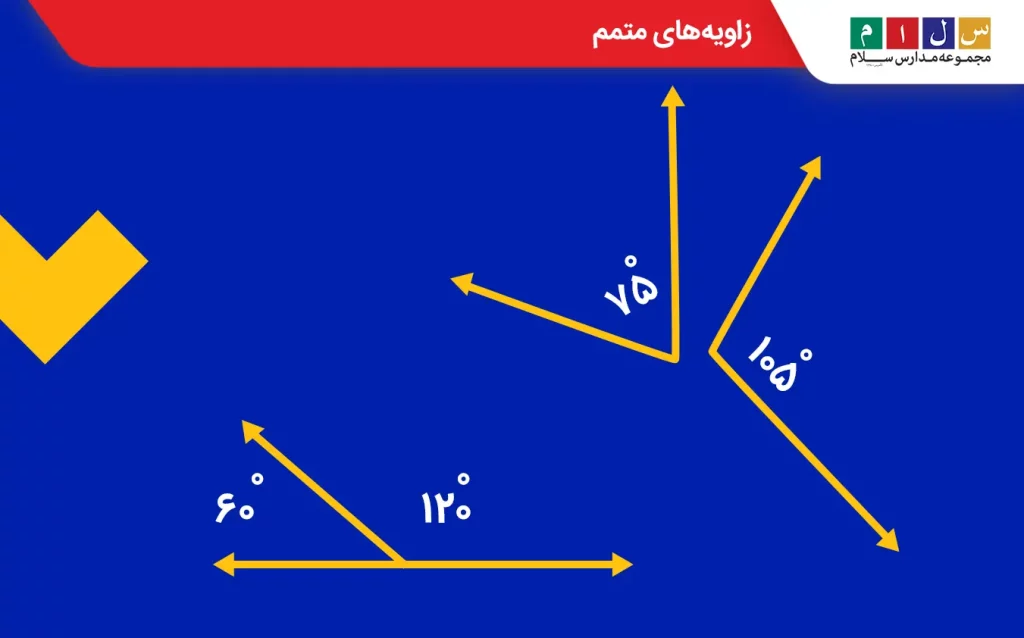
زاویه مکمل
دو زاویهای که مجموع آن‌ها ۱۸۰ درجه باشد را دو زاویه مکمل می‌نامند.
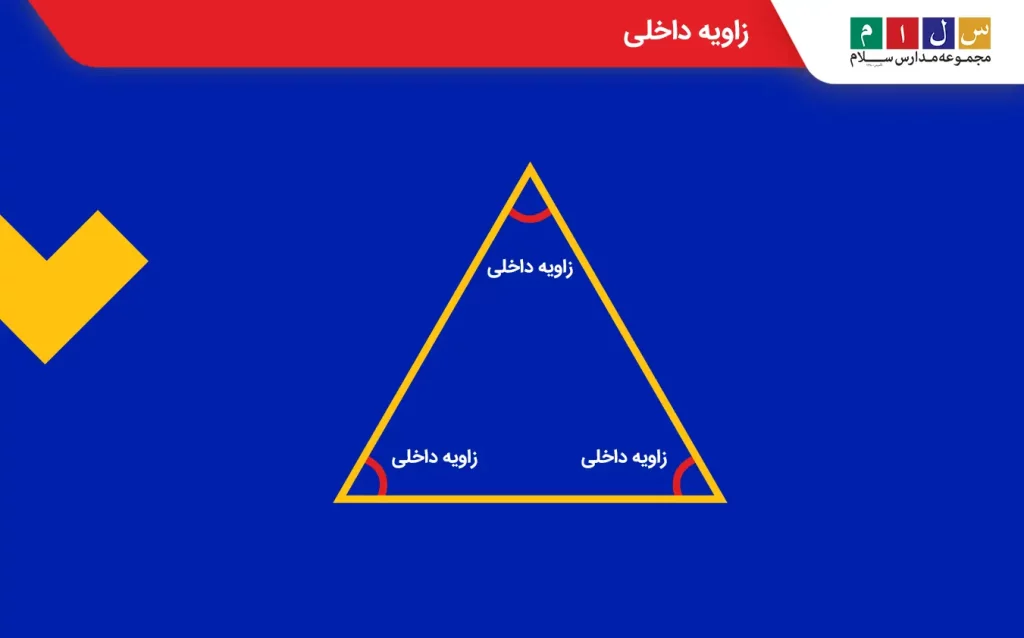
زاویه داخلی
زاویه داخلی زاویهای است که داخل یک شکل قرار دارد. به‌عنوان مثال، یک مثلث دارای سه زاویه داخلی است.
زاویه خارجی
زاویه خارجی همان‌طور که از نامش پیداست، در خارج از شکل و در امتداد اضلاع آن شکل میگیرد. به‌عبارت دیگر، زاویه داخلی و خارجی یک شکل مکمل هم هستند.
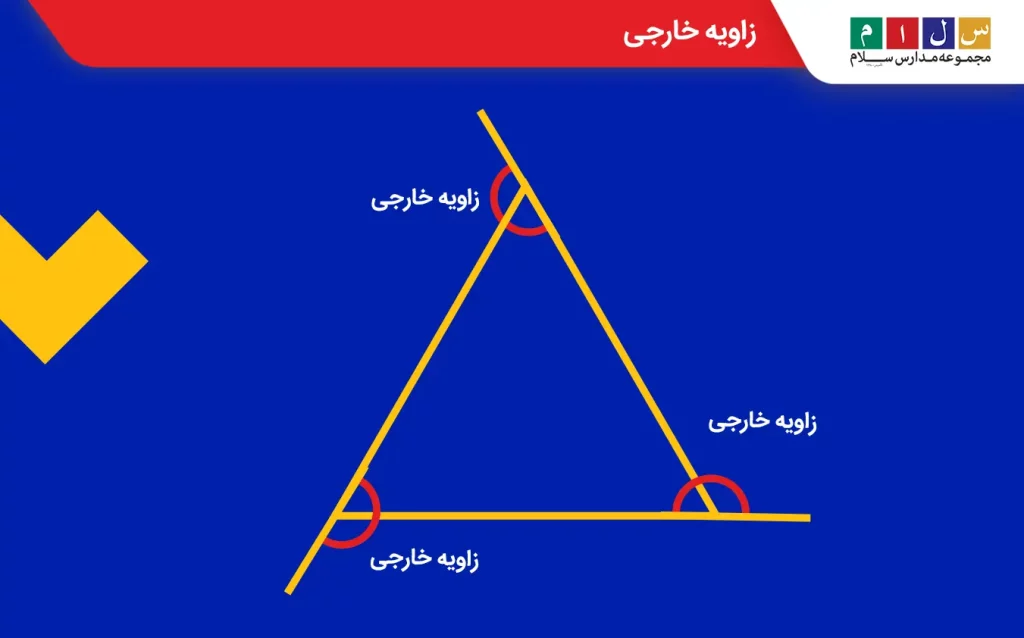
زاویه متقابل به رأس
وقتی دو خط همدیگر را قطع می‌کنند، چهار زاویه تشکیل میشود. زاویههایی که مقابل هم قرار دارند، دوبهدو با هم برابرند. این زاویه‌ها را متقابلبهرأس می‌نامند. برای مثال، در شکل زیر زاویه‌های ۱ و ۳ و زاویه‌های ۲ و ۴ متقابلبهرأس هستند.
مثال ۱: زاویه متمم و مکمل ۷۳ درجه را تعیین کنید.
جواب: زاویه متمم ۷۳ درجه زاویهای است که اگر با ۷۳ جمع شود، حاصل آن ۹۰ درجه میشود. پس باید ۷۳ درجه را از ۹۰ درجه کم کنیم تا زاویه متمم این زاویه به‌دست آید.
۹۰ = زاویه متمم + ۷۳
۱۷ = ۷۳ – ۹۰ = زاویه متمم
زاویه مکمل ۷۳ درجه زاویهای است که اگر با آن جمع شود، حاصل ۱۸۰ درجه است. . بنابراین، باید ۷۳ درجه را از ۱۸۰ درجه کم کنیم تا زاویه مکمل این زاویه به‌دست آید.
۱۸۰ = زاویه مکمل + ۷۳
۱۰۷ = ۷۳ – ۱۸۰ = زاویه مکمل
مثال ۲: زاویه داخلی و خارجی یک مثلث متساوی‌الاضلاع چقدر است؟
جواب: مثلث متساوی‌الاضلاع سه ضلع و سه زاویه برابر دارد که اندازه آن‌ها ۶۰ درجه است. بنابراین، اندازه سه زاویه داخلی مثلث برابر است با ۶۰ درجه.
برای به‌دست آوردن زاویه خارجی هم کافی‌ست اضلاع را امتداد دهید. البته چون این نوع مثلث سه زاویه داخلی برابر دارد، سه زاویه خارجی آن هم برابر خواهد بود.
همان‌طور که در شکل زیر مشاهده می‌کنید، زاویه داخلی و خارجی، یک زاویه نیمصفحه تشکیل می‌دهند. به‌عبارت دیگر، این دو زاویه مکمل هم هستند. بنابراین، زاویه خارجی این نوع مثلث برابر است با
۱۸۰ = زاویه خارجی + زاویه داخلی
۱۸۰ = زاویه خارجی + ۶۰
۱۲۰ = ۶۰ – ۱۸۰ = زاویه خارجی
مثال ۳: اندازه زاویه (۱) و (۳) را در شکل زیر به‌دست آورید.
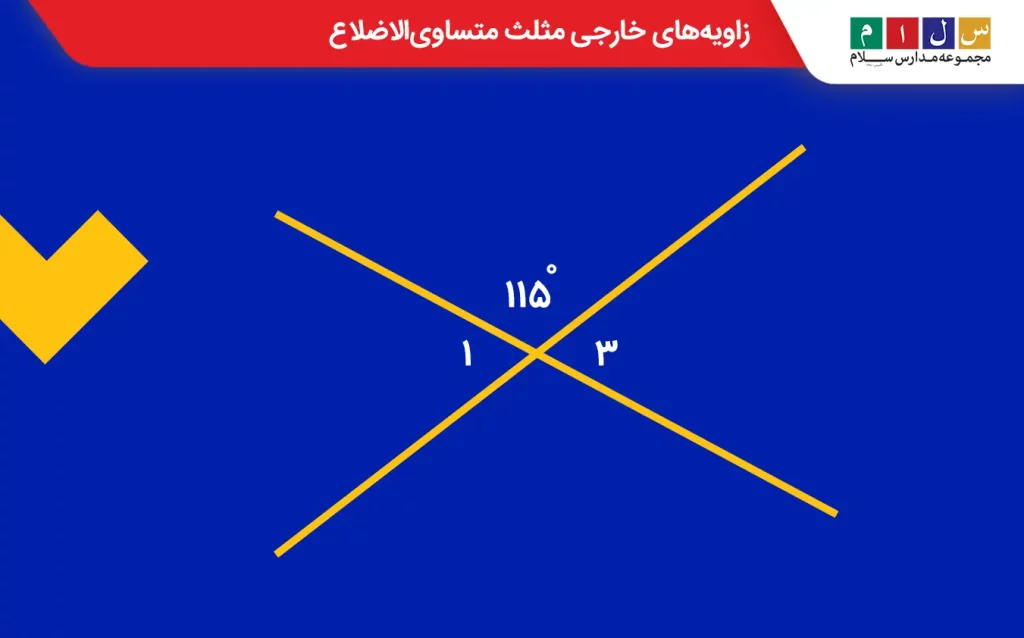
جواب: ابتدا زاویه (۱) را به‌دست می‌آوریم. زاویه (۱) و ۱۱۵ درجه مکمل هم هستند و مجموع آن‌ها برابر با ۱۸۰ درجه است. بنابراین اندازه زاویه (۱) برابر است با
۱۸۰ = ۱۱۵ + زاویه (۱)
۶۵ = ۱۱۵ – ۱۸۰ = زاویه (۱)
ازآنجا که زاویه (۱) و (۳) متقابلبهرأس هستند، اندازه زاویه (۳) نیز برابر با اندازه زاویه (۱) و ۶۵ درجه است.
مثال ۴: اندازه زاویه خواسته‌شده در شکل زیر را تعیین کنید.
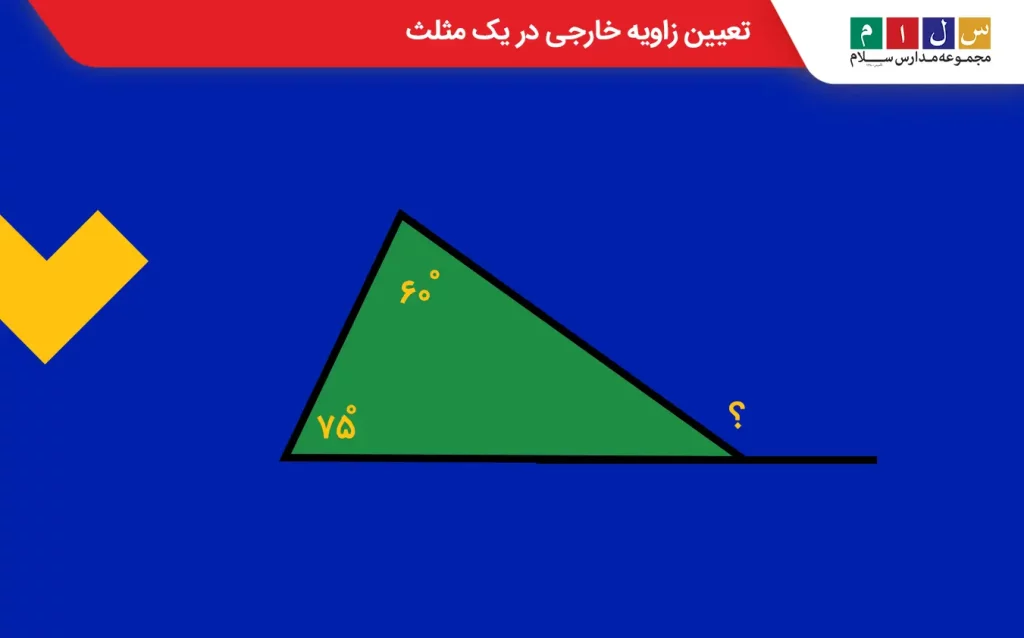
جواب: مجموع زاویه‌های یک مثلث ۱۸۰ درجه است. پس اندازه زاویه سوم مثلث بالا به‌شکل زیر محاسبه میشود:
۱۸۰ = زاویه سوم مثلث + ۶۰ + ۷۵
۱۸۰ = زاویه سوم مثلث + ۱۳۵
۴۵ = ۱۳۵ – ۱۸۰ = زاویه سوم مثلث
حالا که اندازه زاویه سوم مثلث به‌دست آمد، به‌راحتی می‌توانیم زاویه مجهول را تعیین کنیم، زیرا این زاویه و زاویه مجهول مکمل هم هستند و با هم یک زاویه نیمصفحه می‌سازند.
۱۸۰ = زاویه سوم مثلث + زاویه مجهول
۱۸۰ = ۴۵ + زاویه مجهول
۱۳۵ = ۴۵ – ۱۸۰ = زاویه مجهول
پیشنهاد مطالعه: میانگین چیست؟
سخن پایانی
زاویه یکی از مفاهیم هندسی است که از برخورد دو نیمخط ایجاد میشود. محل برخورد دو نیمخط زاویه را رأس زاویه میگویند. بنابراین، یک زاویه از یک رأس و دو نیمخط یا دو ضلع ساخته شده است. زاویه را با وسیلهای نیم‌دایره‌ای‌شکل بهنام نقاله و برحسب درجه اندازه میگیرند. هرچه میزان بازشدگی دو نیمخط زاویه بیشتر باشد، آن زاویه بزرگ‌تر است. زاویه براساس اندازه و محل قرارگیری در اشکال مختلف به چند نوع طبقه‌بندی میشود که در این آموزش هر یک از آن‌ها را جداگانه مورد بررسی قرار دادیم.
سؤالات متداول
- زاویه چیست؟
از برخورد دو نیمخط زاویه تشکیل میشود. محل برخورد دو نیمخط را رأس زاویه میگویند. - زاویه را چگونه اندازه میگیرند؟
برای اندازه گیری زاویه از وسیلهای بهنام نقاله استفاده میشود. بهاین صورت که ابتدا مرکز نقاله را روی رأس زاویه قرار میدهیم و خط مبنا (صفر نقاله) را روی یک ضلع زاویه منطبق میکنیم. عددی که ضلع دوم روی آن منطبق شده است، اندازه زاویه را به ما نشان میدهد. - زاویه حاده چیست؟
زاویه کمتر از ۹۰ درجه را زاویه حاده یا تند میگویند. - زاویه منفرجه چیست؟
زاویه منفرجه یا باز زاویهای است که اندازه آن بین ۹۰ تا ۱۸۰ درجه است. - زاویه قائمه چیست؟
زاویه ۹۰ درجه را زاویه قائمه یا راست میگویند. - زاویه نیمصفحه و تمامصفحه چند درجه است؟
زاویه نیمصفحه ۱۸۰ درجه و زاویه تمامصفحه ۳۶۰ درجه است. - زاویه متمم چه تفاوتی با زاویه مکمل دارد؟
اگر مجموع دو زاویه ۹۰ درجه باشد، دو زاویه را متمم و اگر مجموع دو زاویه ۱۸۰ درجه باشد، دو زاویه را مکمل میگوییم. - زاویه داخلی و خارجی چه زاویههایی هستند؟
زاویه داخلی زاویهای است که داخل شکل قرار دارد، اما زاویه خارجی زاویهای است که در خارج از شکل و درامتداد اضلاع آن شکل میگیرد. - زاویه متقابلبهرأس چیست؟
اگر دو خط همدیگر را قطع کنند، چهار زاویه ایجاد میشود. زاویههایی که مقابل هم هستند و دوبهدو هماندازهاند را متقابلبهرأس میگویند.
