فهرست مطالب
Toggleدر این مقاله قصد داریم یکی دیگر از انواع مثلثها بهنام مثلث مختلف الاضلاع را معرفی کنیم. در این نوع مثلث همانطور که از نامش پیداست هیچ یک از اضلاع و زوایا با هم مساوی نیستند. برای اینکه مثلث مختلف الاضلاع و ویژگیهای آن را بهتر بشناسید و روش محاسبه محیط و مساحت آن را بیاموزید، پیشنهاد میکنیم با ادامه این مطلب همراه ما باشید.
مثلث مختلف الاضلاع چیست؟
مثلث شکلی هندسی است با سه ضلع و سه زاویه که مجموع زاویههای داخلی آن همیشه ۱۸۰ درجه است.
بر اساس تعریف مثلث مختلف الاضلاع، مثلثی است که طول هر سه ضلع و اندازه هر سه زاویه داخلی آن متفاوت است. بهعبارت دیگر، در مثلث مختلف الاضلاع هیچ یک از دو ضلع یا دو زاویه با هم برابر نیستند.
شکل زیر بهخوبی تفاوت اضلاع و زوایا را در این نوع مثلث نشان میدهد.

پیشنهاد مطالعه: مثلث متساوی الساقین چیست؟
ویژگی های مثلث مختلف الاضلاع
مثلث مختلف الاضلاع بهعنوان مثلثی که زوایا و اضلاع آن یکسان نیستند، ویژگیهایی دارد که در زیر به آنها اشاره میکنیم:
- مثلث مختلف الاضلاع ۳ ضلع و ۳ زاویه داخلی نامساوی دارد.
- مجموع زوایای داخلی این نوع مثلث برابر ۱۸۰ درجه است.
- مثلث مختلف الاضلاع ۳ ارتفاع با طولهای متفاوت دارد.
- این مثلث بهدلیل نداشتن اضلاع برابر متقارن نیست و درنتیجه خط تقارن ندارد.
- مثلث مختلف الاضلاع دارای تقارن مرکزی و تقارن چرخشی نیست.
- زوایای داخلی یک مثلث مختلف الاضلاع میتواند حاده، منفرجه یا قائمه باشد.

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
انواع مثلث مختلف الاضلاع
مثلث مختلف الاضلاع را براساس اندازه زوایای آن میتوان به سه دسته تقسیمبندی کرد:
- مثلث مختلف الاضلاع حاده
- مثلث مختلف الاضلاع منفرجه
- مثلث مختلف الاضلاع قائمالزاویه
مثلث مختلف الاضلاع حاده
مثلث مختلفالاضلاعی که تمام زوایای داخلی آن حاده باشد یعنی اندازه آنها کمتر از ۹۰ درجه باشد، مثلث مختلف الاضلاع حاده نام دارد. همانطور که در شکل زیر هم مشاهده میکنید، اندازه هر سه زاویه مثلث نشاندادهشده کمتر از ۹۰ درجه است.

مثلث مختلف الاضلاع منفرجه
اگر در یک مثلث مختلف الاضلاع یکی از زاویهها منفرجه باشد یعنی اندازه آن بین ۹۰ و ۱۸۰ درجه باشد و دو زاویه دیگر حاده باشند، آن را مثلث مختلف الاضلاع منفرجه مینامیم. در شکل زیر میتوانید نمونهای از این نوع مثلث را مشاهده کنید.

مثلث مختلف الاضلاع قائم الزاویه
در مثلث مختلف الاضلاع قائمالزاویه یکی از زوایا قائمه (۹۰ درجه) و دو زاویه دیگر حاده هستند.

پیشنهاد مطالعه: مثلث قائمالزاویه چیست؟
مثلث مختلف الاضلاع چند محور تقارن دارد؟
خط تقارن خطی است که شکل را به دو قسمت کاملاً مساوی و قرینه تقسیم میکند. در مثلث مختلف الاضلاع هیچ دو ضلع برابری وجود ندارد. به همین خاطر، همانطور که در تصویر زیر هم مشاهده میکنید، این نوع مثلث متقارن نیست و هیچ خط تقارنی ندارد.

آیا مثلث مختلف الاضلاع مرکز تقارن دارد؟
یک شکل هندسی درصورتی مرکز تقارن دارد که اگر آن را بهاندازه ۱۸۰ درجه بچرخانیم، دوباره به حالت اول خود برگردد و روی خودش منطبق شود. مثلث مختلف الاضلاع بهدلیل ویژگیهای ظاهریاش مانند سایر مثلثها تقارن مرکزی و درنتیجه مرکز تقارن ندارد.

محیط مثلث مختلف الاضلاع
محیط مثلث از مجموع اضلاع آن بهدست میآید. اگر اضلاع یک مثلث مختلف الاضلاع را با a، b و c و محیط آن را با P نشان دهیم، فرمول محیط مثلث مختلف الاضلاع بهصورت زیر خواهد بود:
P = a + b + c
نکته: واحد اندازهگیری محیط همان واحد اندازهگیری طول اضلاع است. برای مثال، اگر طول اضلاع برحسب میلیمتر باشد، محیط نیز برحسب میلیمتر خواهد بود.

مثال: محیط مثلث زیر را تعیین کنید.

مساحت مثلث مختلف الاضلاع
مساحت مثلث برابر است با اندازه سطح داخلی آن. فرمول رایج برای محاسبه مساحت مثلث مختلف الاضلاع که برای انواع مثلث مورد استفاده قرار میگیرد، بهصورت زیر است:
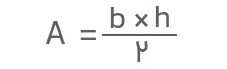
- A: مساحت مثلث مختلف الاضلاع
- b: قاعده مثلث مختلف الاضلاع
- h: ارتفاع مثلث مختلف الاضلاع
اگر مقدار ارتفاع و قاعده مثلث را نداشته باشیم و تنها اندازه اضلاع آن مشخص باشد، از فرمول هرون استفاده میکنیم:
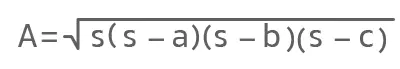
در اینجا a، b و c طول اضلاع مثلث و s نصف محیط آن است.
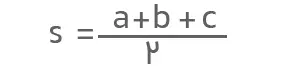
نکته: واحد اندازهگیری مساحت برحسب واحد مربع است. بهعنوان مثال، اگر اندازه اضلاع برحسب سانتیمتر باشد، مساحت برحسب سانتیمتر مربع خواهد بود.

مثال ۱: مساحت مثلث زیر را بیابید.

مثال ۲: مساحت مثلثی را بهدست آورید که طول اضلاع آن ۳، ۴ و ۵ سانتیمتر است.
جواب: با توجه به اینکه اندازه سه ضلع داده شده است، از فرمول هرون استفاده میکنیم. برای محاسبه مساحت این مثلث به کمک فرمول هرون ابتدا باید نصف محیط مثلث را بهدست آوریم. داریم:
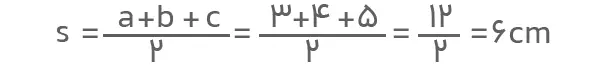
بنابراین، مساحت مثلث برابر است با
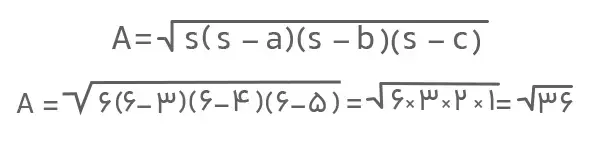
سخن پایانی
در این آموزش با مثلث مختلف الاضلاع آشنا شدیم و گفتیم که این نوع مثلث یک سهضلعی غیرمنتظم است که هیچ دو ضلع یا دو زاویه برابری ندارد و از این جهت آن را مختلفالاضلاع مینامند. مثلث مختلف الاضلاع ازنظر اندازه زاویه به سه نوع حاده، منفرجه و قائمالزاویه دستهبندی میشود که در این مقاله هر یک از آنها را با شکل توضیح دادیم. همچنین درمورد فرمول محیط و مساحت این مثلث صحبت کرده و برای هر یک مثال حلشدهای ارائه کردیم. امیدواریم این آموزش برایتان مفید بوده باشد.
سؤالات متداول
- تعریف مثلث مختلف الاضلاع چیست؟
مثلث مختلف الاضلاع به مثلثی گفته میشود که هیچ کدام از اضلاع و زوایای آن برابر نیست. - مجموع زوایای داخلی مثلث مختلف الاضلاع چند درجه است؟
مجموع زوایای داخلی مثلث مختلف الاضلاع ۱۸۰ درجه است. - مثلث مختلف الاضلاع چند خط تقارن دارد؟
مثلث مختلف الاضلاع هیچ خط تقارنی ندارد. - آیا مثلث مختلف الاضلاع مرکز تقارن دارد؟
خیر. مثلث مختلف الاضلاع تقارن مرکزی و درنتیجه مرکز تقارن ندارد. - تعداد قطر مثلث مختلف الاضلاع چند تا است؟
مثلث مختلف الاضلاع مانند سایر مثلثها قطر ندارد. - فرمول محیط مثلث مختلف الاضلاع چیست؟
فرمول محیط مثلث مختلف الاضلاع برابر است با مجموع سه ضلع آن.









