فهرست مطالب
Toggleاز مقالههای محیط و مساحت شروع کردیم و سپس با جزئیات کامل و مثالهای فراوان، محیط و مساحت و حجم اشکال هندسی از مثلث گرفته تا مربع و مکعب را در مقالههایی جداگانه توضیح دادیم. در این مقاله برای دسترسی راحتتر شما والدین و دانشآموزان عزیز، فرمول محیط و مساحت اشکال هندسی را بهصورت خلاصه و در جدول میآوریم. فرمول هر کدام از اشکال هندسی برایتان مبهم بود، روی لینک مقاله اختصاصی محیط یا مساحت آن شکل هندسی بزنید و توضیحات واضح و مثالهای فراوان مرتبط با آن موضوع را مطالعه کنید. به موضوعاتی که در مطلب تفاوت و شباهت اشکال هندسی اشاره شد هم سری بزنید.
محیط و مساحت مثلث
مثلث یکی از اشکال هندسی پایه است که از ۳ راس و ۳ ضلع تشکیل میشود و انواع مختلفی دارد:
- متساویالاضلاع
- مختلفالاضلاع
- متساویالساقین
- قائمالزاویه
- منفرجه
برای محاسبه محیط و مساحت مثلث یک فرمول کلی وجود دارد. البته هر کدام از انواع مثلث را میتوان با فرمول اختصاصی مربوط به آن هم حساب کرد. ما در اینجا ابتدا فرمول عمومی محاسبه محیط و مساحت مثلث و سپس فرمول اختصاصی هر کدام از انواع آن را بیان میکنیم.
فرمول محیط مثلث
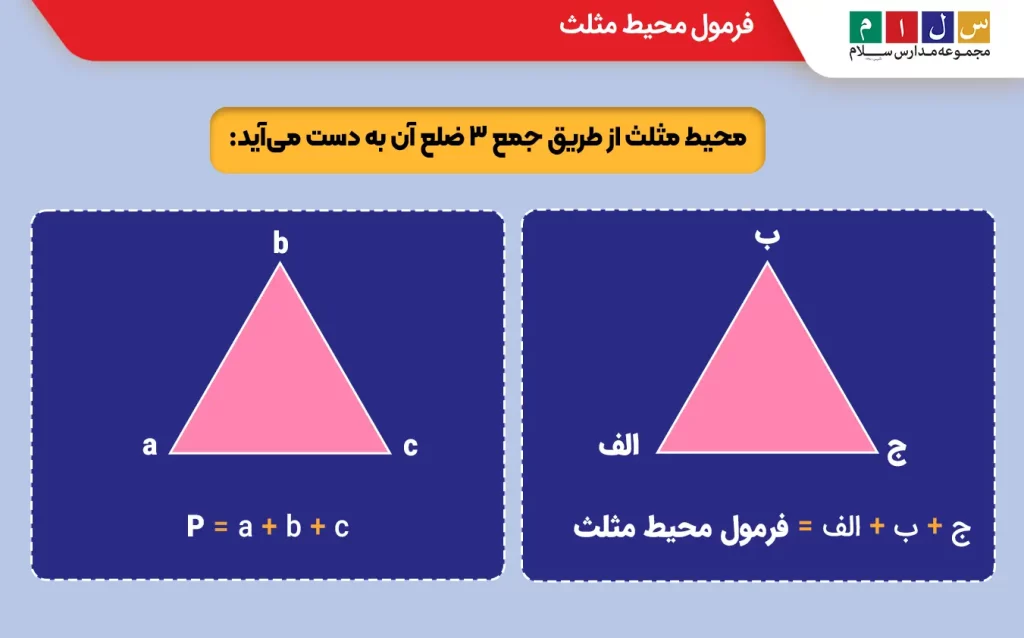
محیط مثلث از طریق جمع ۳ ضلع آن به دست میآید:
ج + ب + الف = فرمول محیط مثلث
یا
P = a + b + c
فرمول مساحت مثلث
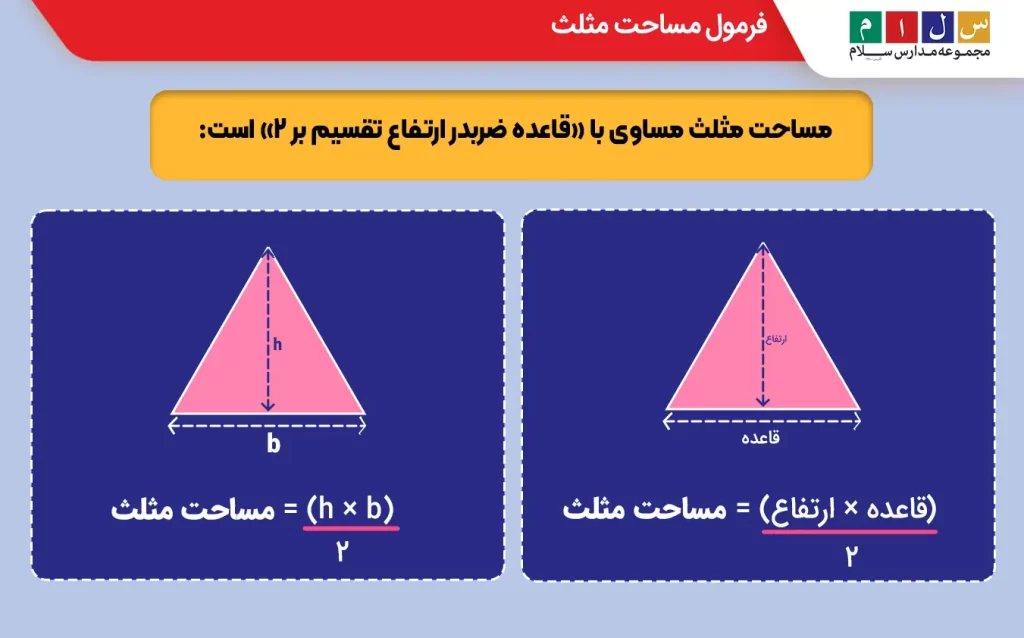
مساحت مثلث مساوی با «قاعده ضربدر ارتفاع تقسیم بر ۲» است:
۲ ÷ ارتفاع × قاعده = مساحت مثلث
فرمول محیط و مساحت مثلث متساوی الاضلاع
هم مساحت مثلث متساوی الاضلاع و هم محیط مثلث متساوی الاضلاع علاوهبر فرمول اصلی با فرمول سریعتری هم قابل محاسبه هستند:
الف × ۳ = الف + الف + الف = محیط مثلث متساویالاضلاع
یا
p = a + a + a= ۳ × a
اندازه یکضلع بهتوان ۲ × ۴ ÷ جذر ۳ = مساحت مثلث متساوی الاضلاع
یا

فرمول محیط و مساحت مثلث مختلف الاضلاع
به دلیل اینکه مثلث مختلفالاضلاع دارای ۳ ضلع نامساویست، برای محاسبه محیط و مساحت آن معمولا از همان فرمولهای اصلی محیط و مساحت مثلث استفاده میشود:
ج + ب + الف = محیط مثلث مختلفالاضلاع
یا
p = a + b + c
۲ ÷ (قاعده × ارتفاع) = مساحت مثلث
A= (h × b) ÷ ۲

پیشنهاد مطالعه : ذوزنقه قائم الزاویه
فرمول محیط و مساحت مثلث متساوی الساقین
مثلث متساویالساقین دارای ۲ ضلع مساوی (ساق) و یک ضلع نامساوی (قاعده) است. برای محاسبه محیط مثلث متساویالساقین و مساحت مثلث متساویالساقین، در کنار فرمول اصلی از فرمولهای زیر هم میتوان استفاده کرد:
ب + الف × ۲ = ب + الف + الف = محیط مثلث متساویالساقین
یا
p = a + a + b= ۲ × a + b
= مساحت مثلث متساویالساقین
(قاعده × 4 ÷ قاعده بهتوان ۲ × اندازه یکی از ساقها بهتوان ۲) جذر × یکدوم
یا

فرمول محیط و مساحت مثلث قائمالزاویه
مثلث قائمالزاویه یک زاویه ۹۰ درجه دارد. در مثلث قائمالزاویه به ۲ ضلع مجاور زاویه ۹۰ درجه قاعده و ارتفاع میگویند و ضلع مقابل زاویه قائمه را «وتر» مینامند. فرمول اختصاصی محیط مثلث قائمالزاویه و مساحت مثلث قائمالزاویه آن به این صورت است:
= محیط مثلث قائمالزاویه
۲ ÷ ضرب اضلاع مجاور زاویه قائمه در یکدیگر = مساحت مثلث قائمالزاویه

فرمول محیط و مساحت مثلث منفرجه
برای محاسبه محیط مثلث منفرجه از فرمول اصلی محیط مثلث استفاده میکنیم. بهدلیل اینکه یکی از اضلاع مثلث منفرجه بیش از ۹۰ درجه است، برای محاسبه مساحت این شکل هندسی:
- باید آن را به مثلث قائمالزاویه تبدیل کنیم.
- با استفاده از فرمول اصلی مساحت مثلث (قاعده ضربدر ارتفاع تقسیم بر ۲)، مساحت آن را محاسبه کنیم.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
محیط و مساحت مربع
مربع دارای ۴ ضلع مساویست و برای محاسبه محیط و مساحتش از فرمولهای زیر استفاده میشود:
فرمول محیط مربع
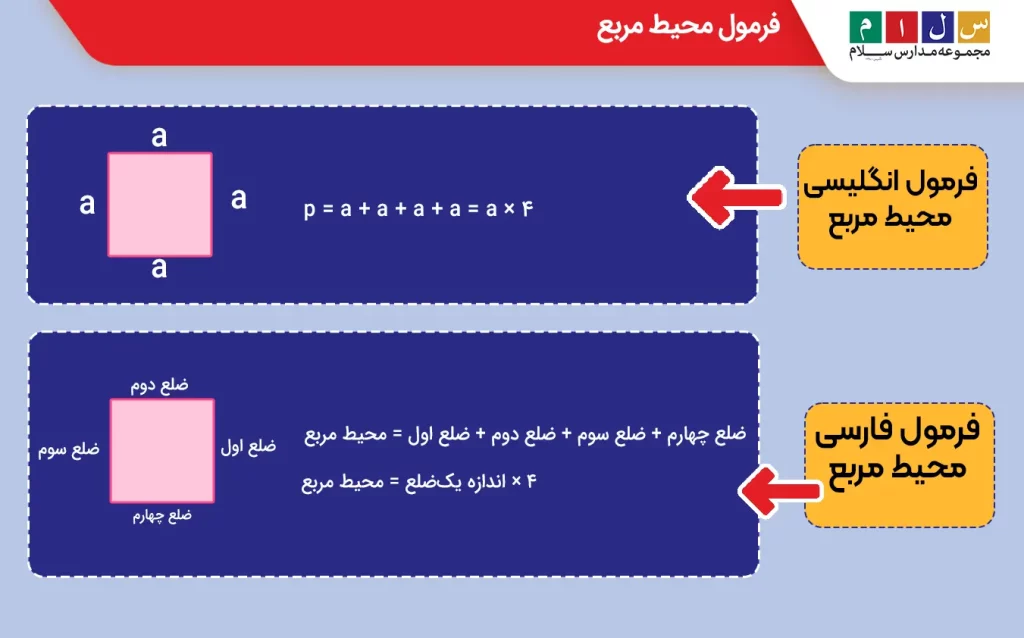
برای محاسبه محیط مربع کافیست ۴ ضلع آن را با یکدیگر جمع کنیم:
۴ × اندازه یکضلع = ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط مربع
یا
p = a + a + a + a = a × ۴
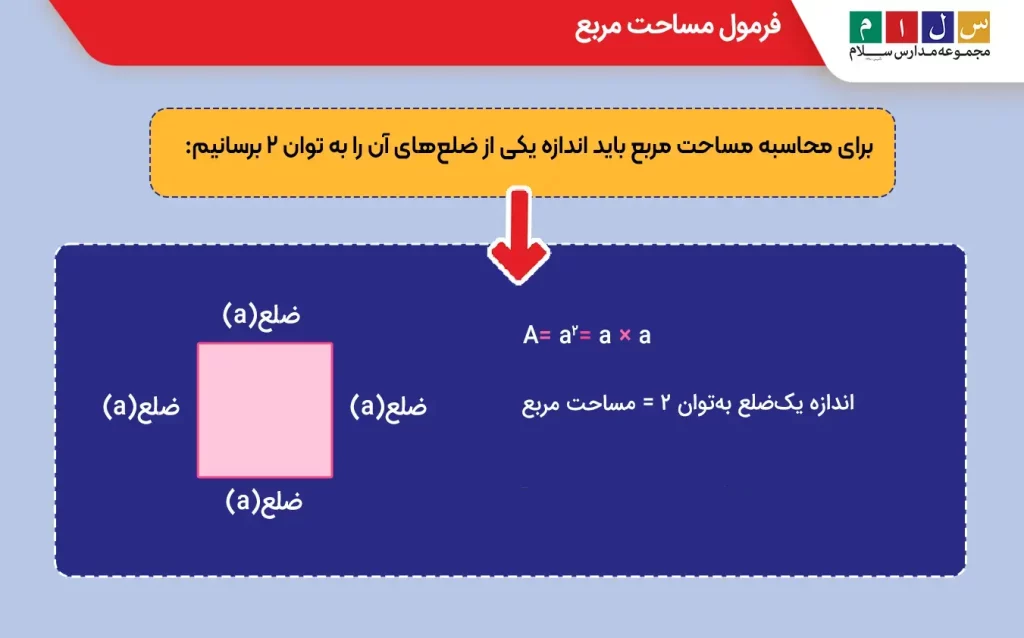
فرمول مساحت مربع
برای محاسبه مساحت مربع باید اندازه یکی از ضلعهای آن را به توان ۲ برسانیم:
خودش × اندازه یک ضلع = اندازه یکضلع بهتوان ۲ = مساحت مربع
یا
A = a² = a × a
محیط و مساحت مستطیل
مستطیل ۴ ضلع دارد که اضلاع آن ۲ به ۲ با یکدیگر مساویاند. برای محاسبه محیط و مساحت مستطیل از فرمولهای زیر استفاده میکنیم:
فرمول محیط مستطیل
برای محاسبه محیط مستطیل، طول و عرض آن را با هم جمع و سپس ضربدر ۲ میکنیم:
(عرض + طول) × ۲ = فرمول محیط مستطیل
یا
P = ۲ × (L+W)

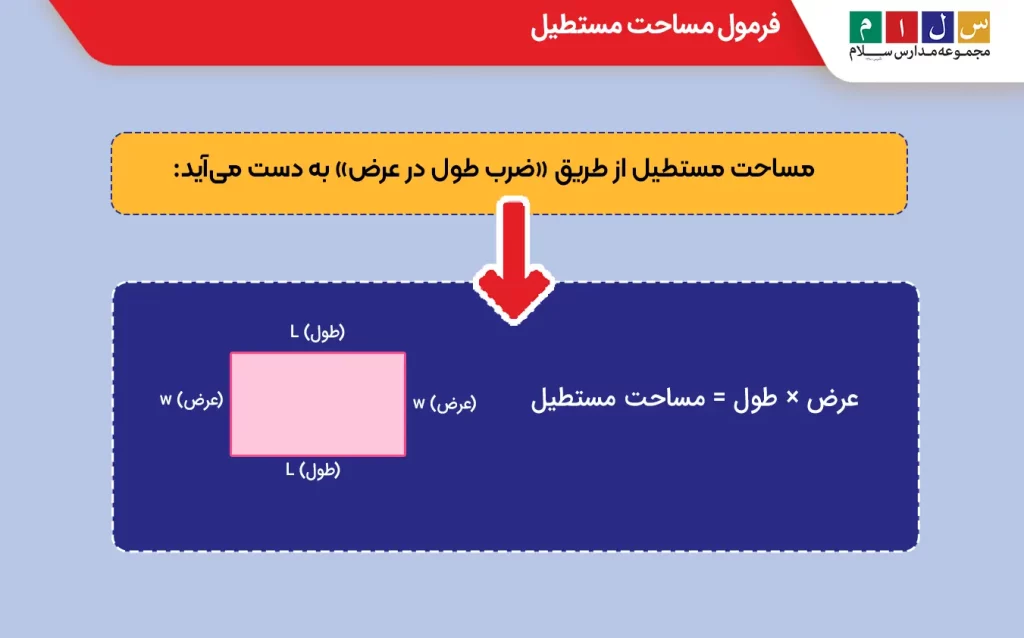
فرمول مساحت مستطیل
مساحت مستطیل از طریق «ضرب طول در عرض» به دست میآید:
عرض × طول = مساحت مستطیل
یا
A= (L × W)
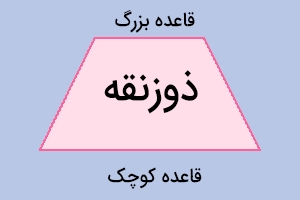
محیط و مساحت ذوزنقه
ذوزنقه یکی از انواع ۴ ضلعیست که ۲ ضلع آن با یکدیگر موازیاند. محیط و مساحت ذوزنقه به کمک فرمولهای زیر به دست میآوریم:
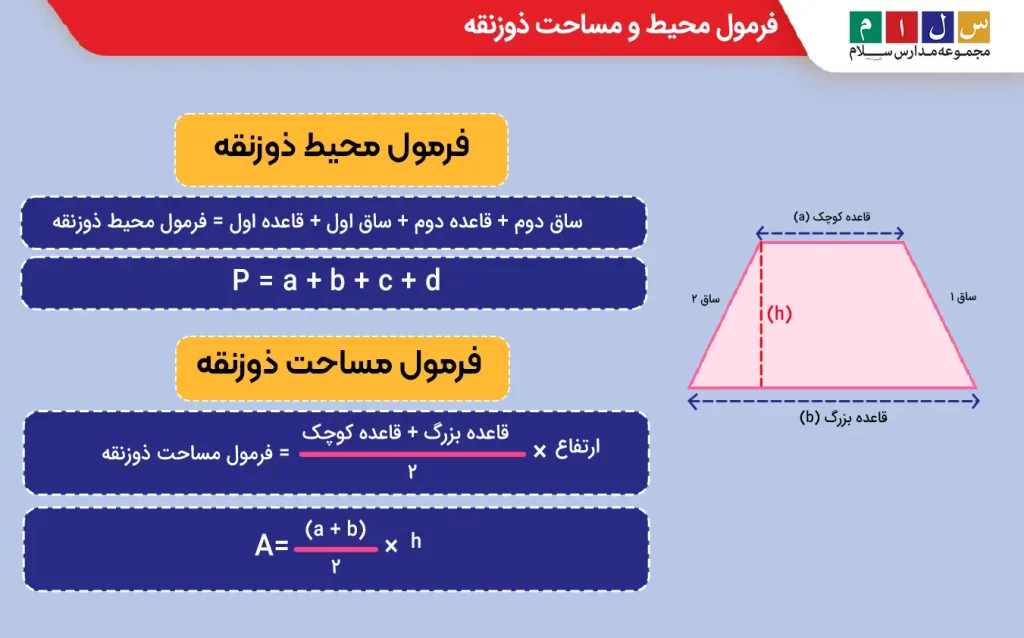
فرمول محیط ذوزنقه
برای بهدستآوردن محیط ذوزنقه از فرمول ساده زیر استفاده میکنیم:
ساق دوم + قاعده دوم + ساق اول + قاعده اول = فرمول محیط ذوزنقه
یا
P = a + b + c + d
فرمول مساحت ذوزنقه
مساحت ذوزنقه مساوی با «جمع ۲ ضلع موازی با یکدیگر، تقسیم بر ۲ ضربدر ارتفاع» است:
ارتفاع × {۲ ÷ ( قاعده بزرگ + قاعده کوچک )} = مساحت ذوزنقه
یا
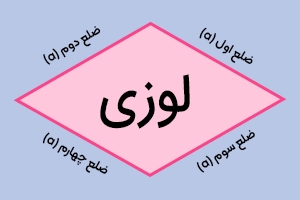
محیط و مساحت لوزی
لوزی ۴ ضلع دارد. این شکل هندسی تا حدودی شبیه مربع و تا حدودی شبیه متوازیالاضلاع است. شبیه مربع است، چون ۴ ضلع آن با هم برابرند و شبیه متوازیالاضلاع است، چون ضلعهای مقابل آن با هم موازیاند. برای محاسبه محیط و مساحت لوزی از فرمولهای زیر استفاده میکنیم:
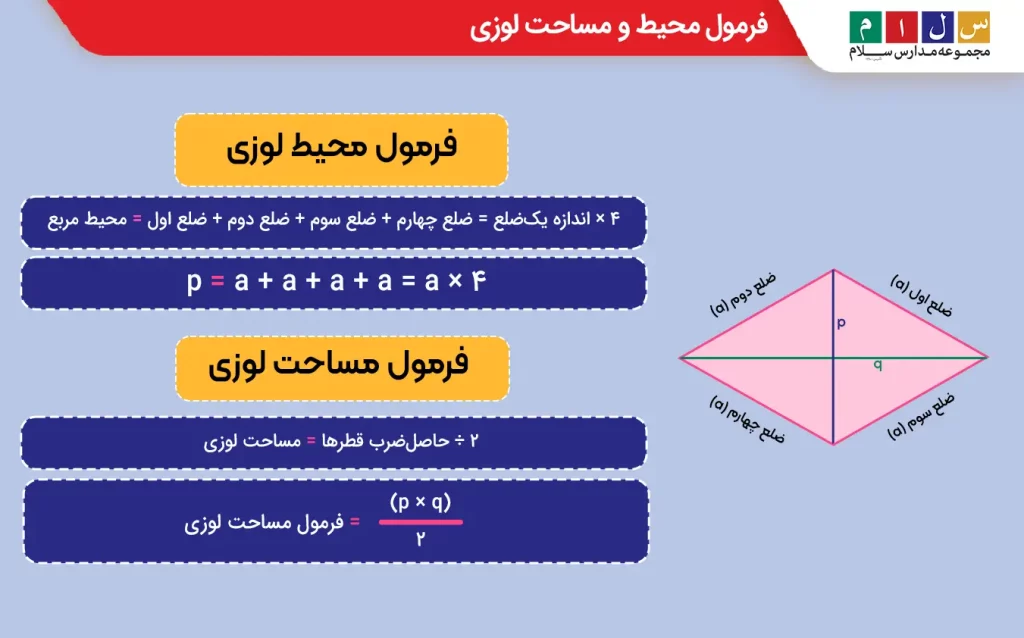
فرمول محیط لوزی
فرمول محیط لوزی دقیقا مثل فرمول محیط مربع نوشته و خوانده میشود:
۴ × اندازه یکضلع = ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط مربع
یا
p = a + a + a + a = a × ۴
فرمول مساحت لوزی
برای محاسبه مساحت لوزی روشهای متعددی وجود دارد که رایجترین آن «حاصلضرب قطرها تقسیم بر ۲» است:
۲ ÷ حاصلضرب قطرها = مساحت لوزی
یا
محیط و مساحت متوازی الاضلاع
متوازیالاضلاع یک ۴ ضلعیست. اضلاع مقابل هم در این شکل هندسی با یکدیگر مساوی و موازیاند. محیط و مساحت متوازیالاضلاع از طریق فرمولهای زیر به دست میآید:
فرمول محیط متوازی الاضلاع
بهدلیل اینکه اضلاع مقابل متوازیالاضلاع با یکدیگر مساویاند، محیط متوازی الاضلاع را از طریق «جمع ۲ ضلع مجاور ضربدر ۲» حساب میکنیم:
۲ × جمع دو ضلع مجاور = محیط متوازی الاضلاع
یا
P = ۲ × a + b
فرمول مساحت متوازی الاضلاع
مساحت متوازی الاضلاع را با ضرب قاعده و ارتفاع آن در یکدیگر محاسبه میکنیم:
ارتفاع × قاعده = مساحت متوازی الاضلاع
یا
A=b × h

محیط و مساحت دایره
محیط و مساحت دایره از طریق فرمولهای زیر به دست میآیند:
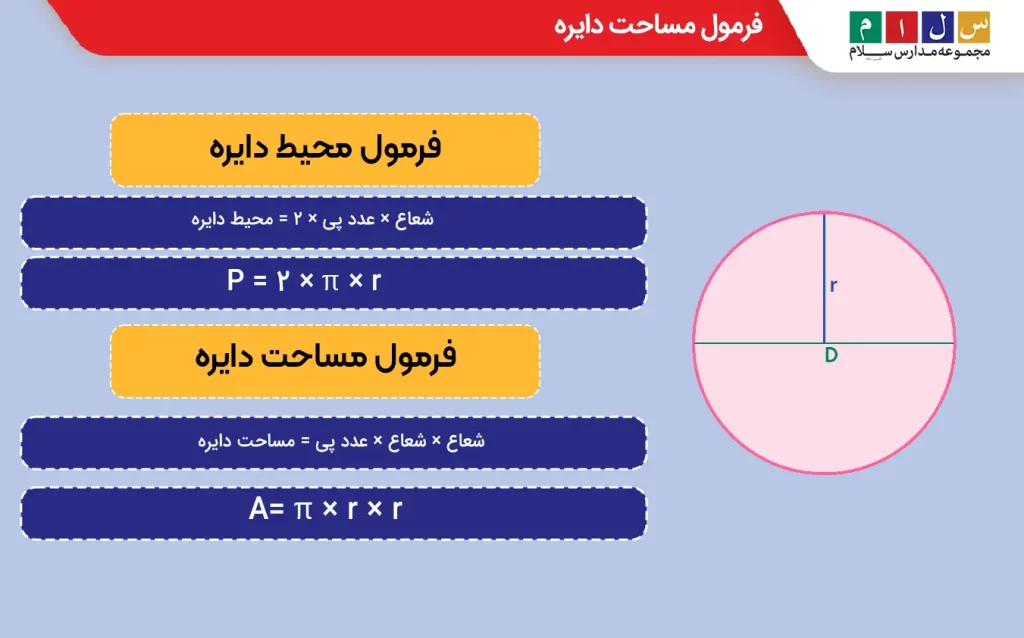
فرمول محیط دایره
محیط دایره از طریق فرمول زیر محاسبه میشود:
شعاع × عدد پی × ۲ = محیط دایره
یا
P = ۲ × π × r
فرمول مساحت دایره
مساحت دایره را معمولا با استفاده از شعاع آن محاسبه میکنند:
شعاع × شعاع × عدد پی = مساحت دایره
یا
A = π × r × r
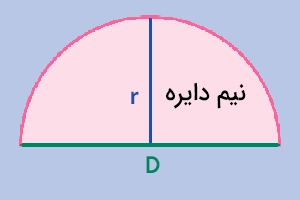
محیط و مساحت نیم دایره
برای محاسبه محیط و مساحت نیمدایره از فرمولهای زیر استفاده میکنیم:
فرمول محیط نیم دایره
رایجترین فرمول محیط نیم دایره مساوی با «قطر + نصف محیط دایره» است:
(۲ ÷ محیط دایره) + قطر = محیط نیم دایره
یا
فرمول مساحت نیم دایره
برای مساحت نیم دایره کافیست مساحت دایره را محاسبه و سپس تقسیم بر ۲ کنیم:
۲ ÷ (شعاع × شعاع × ۳/۱۴) = مساحت نیم دایره
یا
A= (۳.۱۴ × r × r × r) ÷ ۲

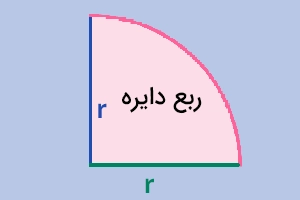
محیط و مساحت ربع دایره
محیط و مساحت ربعدایره را از طریق فرمولهای زیر به دست میآوریم:
محیط ربع دایره
محیط دایره مساوی با یکچهارم محیط دایره بهاضافه شعاع ضربدر ۲ است، بنابراین برای محیط ربع دایره داریم:
(۲ × شعاع) + (۴ ÷ محیط دایره) = محیط ربع دایره
یا
P = (۲ × π × r) + (r × ۲)
مساحت ربع دایره
مساحت ربع دایره مساوی با مساحت دایره تقسیم بر ۴ است:
۴ ÷ شعاع × شعاع × ۳/۱۴ = مساحت ربع دایره
یا
۴ ÷ (r × r × ۳/۱۴) = A

محیط و مساحت هرم
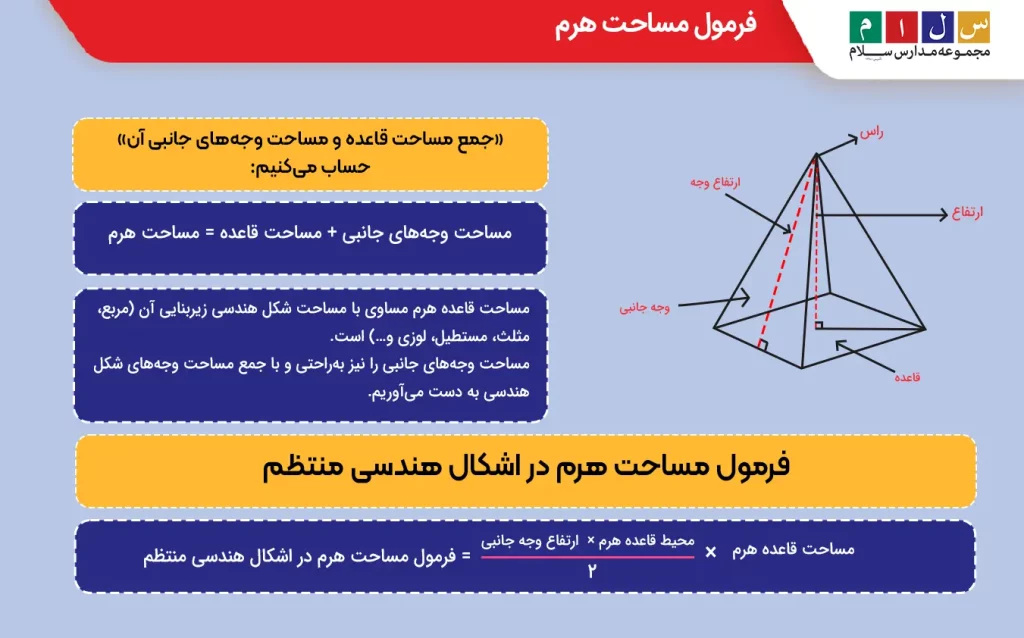
هرم یکی از اشکال هندسی سهبعدیست. مساحت این شکل هندسی را از طریق «جمع مساحت قاعده و مساحت وجههای جانبی آن» حساب میکنیم:
مساحت وجههای جانبی + مساحت قاعده = مساحت هرم
در فرمول بالا:
- مساحت قاعده هرم مساوی با مساحت شکل هندسی زیربنایی آن (مربع، مثلث، مستطیل، لوزی و…) است.
- مساحت وجههای جانبی را نیز بهراحتی و با جمع مساحت وجههای شکل هندسی به دست میآوریم.
البته برای محاسبه مساحت هرم در شکلهای هندسی منتظم میتوان از فرمول سادهتری استفاده کرد:
فرمول مساحت هرم در اشکال هندسی منتظم =
(محیط قاعده هرم × ارتفاع وجه جانبی) ÷ (مساحت قاعده هرم × ۲)
یا
محیط و مساحت مکعب
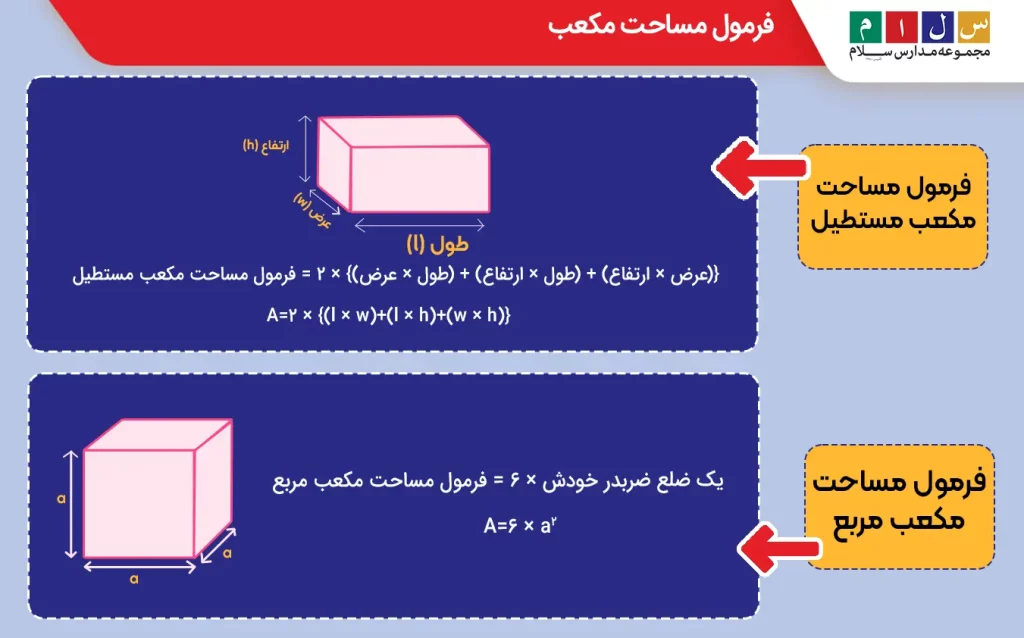
بستگی به شکل هندسی مکعب دارد؛ بهعنوانمثال، برای محاسبه مساحت مکعب از فرمول زیر استفاده میکنیم:
{(عرض × ارتفاع) + (طول × ارتفاع) + (طول × عرض)} × ۲ = فرمول مساحت مکعب مستطیل
یا
A = ۲ × {(l × w)+(l × h)+(w × h)}
باتوجه به اینکه طول، عرض و ارتفاع مربع با هم برابرند، فرمول محاسبه مساحت مکعب مربع به این شکل در میآید:
یک ضلع ضربدر خودش × ۶ = فرمول مساحت مکعب مربع
یا
A = ۶ × a²
پیشنهاد مطالعه: محیط و مساحت مکعب
محیط و مساحت استوانه
استوانه از ۲ دایره بالایی و پایانی و یک حلقه میانی که هنگام بازشدن به شکل مستطیل در میآید، تشکیل شده است. پس برای محاسبه مساحت استوانه داریم:
(ارتفاع × محیط دایره × ۲) + (مساحت دایره × ۲) = مساحت استوانه
یا
A = ۲r۲+ ۲rh

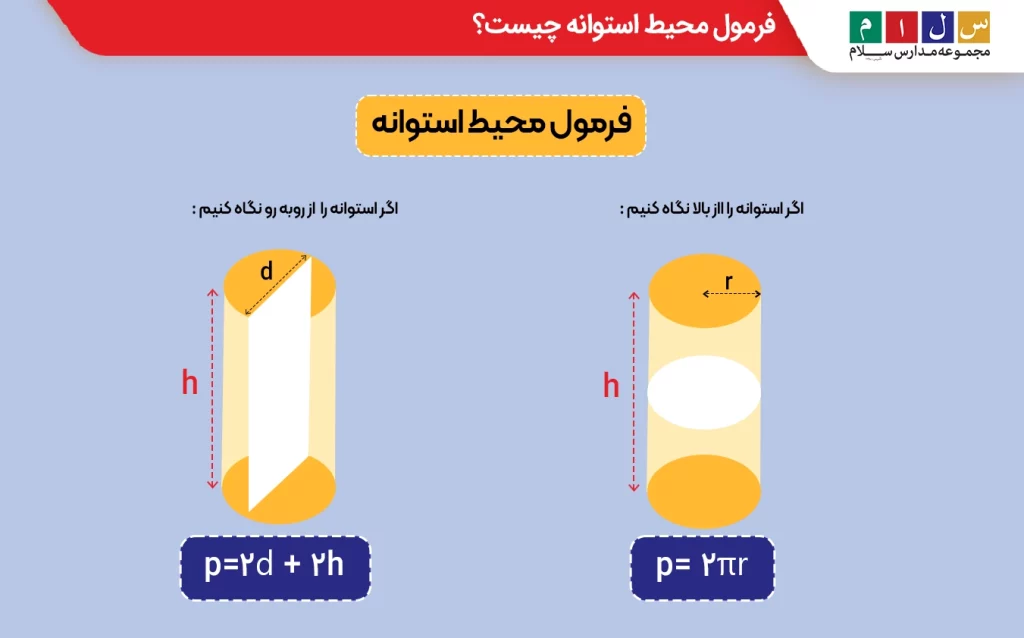
مفهوم محیط معمولاً در اشکال دوبعدی تعریف میشود و بهکار بردن آن برای اشکال سهبعدی شاید عجیب به نظر برسد. اگر بخواهیم محیط استوانه را بهدست آوریم، باید مانند اشکال دوبعدی آن را در صفحهای دوبعدی تجسم کنیم. همانطور که در شکل زیر هم نشان دادهایم، دو حالت خواهیم داشت:
- اگر استوانه را از بالا نگاه کنیم، قاعدههای دایرهای شکل را خواهیم دید که در این صورت، محیط استوانه برابر با محیط قاعده یعنی محیط دایرهای به شعاع r خواهد بود:
P=۲πr
- اگر از روبهرو سطح جانبی استوانه را ببینیم، مستطیلی را مشاهده میکنیم که طول آن برابر با ارتفاع استوانه و عرض آن مساوی با قطر قاعده است. در این حالت، محیط استوانه برابر با محیط این مستطیل خواهد بود:
P=۲d+۲h
d قطر قاعده و h ارتفاع استوانه است.
حجم و مساحت کره
کره از اشکال هندسی ۳ بعدیست که از روبهرو شبیه دایره به نظر میرسد. مساحت و حجم کره را به این صورت حساب میکنیم:
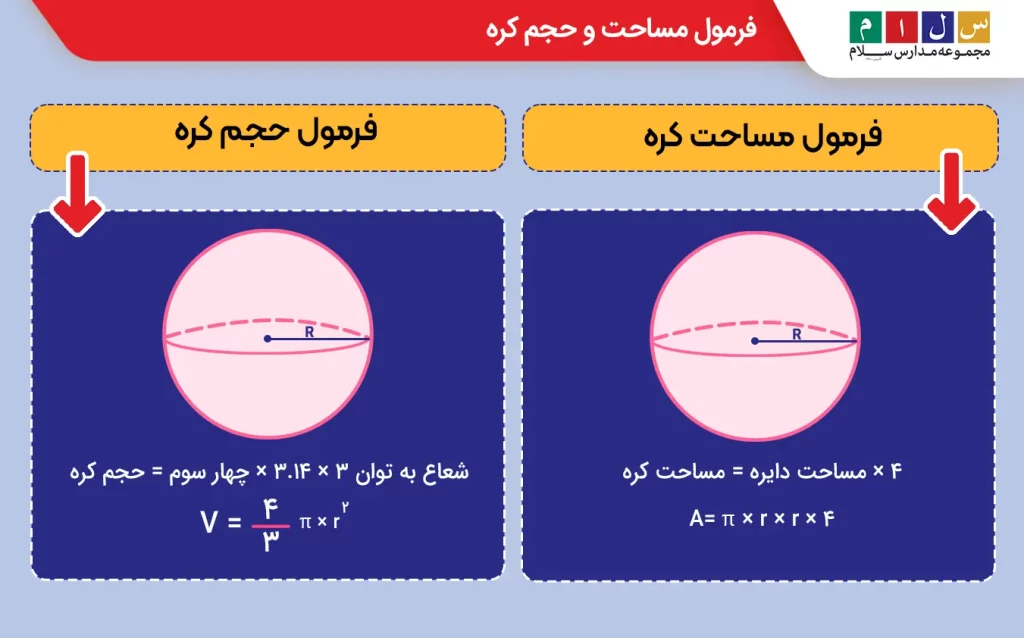
فرمول مساحت کره
مساحت کره ۴ برابر مساحت دایره است:
۴ × مساحت دایره = مساحت کره
A = π × r × r × ۴
فرمول حجم کره
حجم کره به شکل زیر به دست میآید:
شعاع به توان ۳ × ۳.۱۴ × چهار سوم = حجم کره
یا
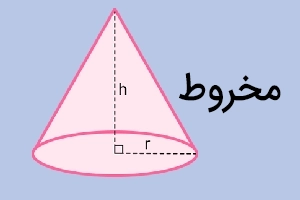
حجم و مساحت مخروط
مخروط یکی از انواع هرم است که قاعده آن به شکل دایره است. برای محاسبه مساحت و حجم مخروط از فرمولهای زیر استفاده میکنیم:
فرمول مساحت مخروط
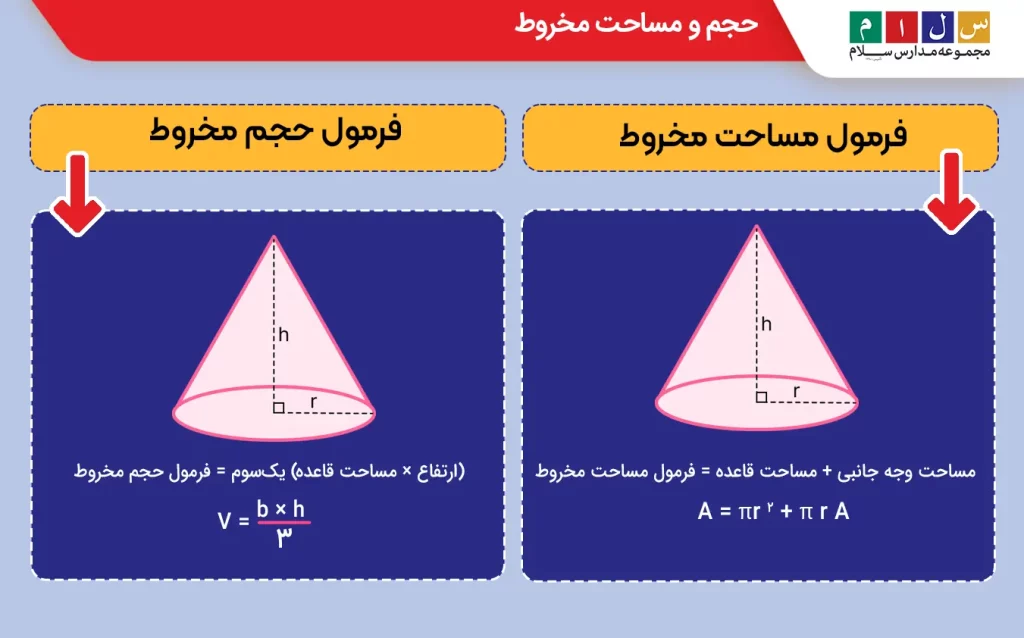
برای محاسبه مساحت مخروط، باید مساحت قاعده این شکل هندسی را با مساحت وجه جانبی آن جمع کنیم:
مساحت وجه جانبی + مساحت قاعده = فرمول مساحت مخروط
یا
A = πr۲ + πra
پیشنهاد مطالعه: محیط و مساحت مخروط
فرمول حجم مخروط
حجم مخروط، یکسوم مساحت قاعده این شکل هندسی در ارتفاع آن است:
(ارتفاع × مساحت قاعده) یکسوم = فرمول حجم مخروط
یا
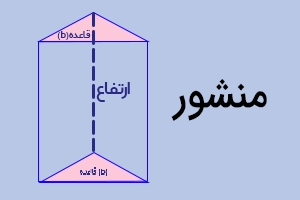
مساحت و حجم منشور
برای محاسبه مساحت و حجم منشور از فرمولهای زیر استفاده میکنیم:
فرمول مساحت منشور
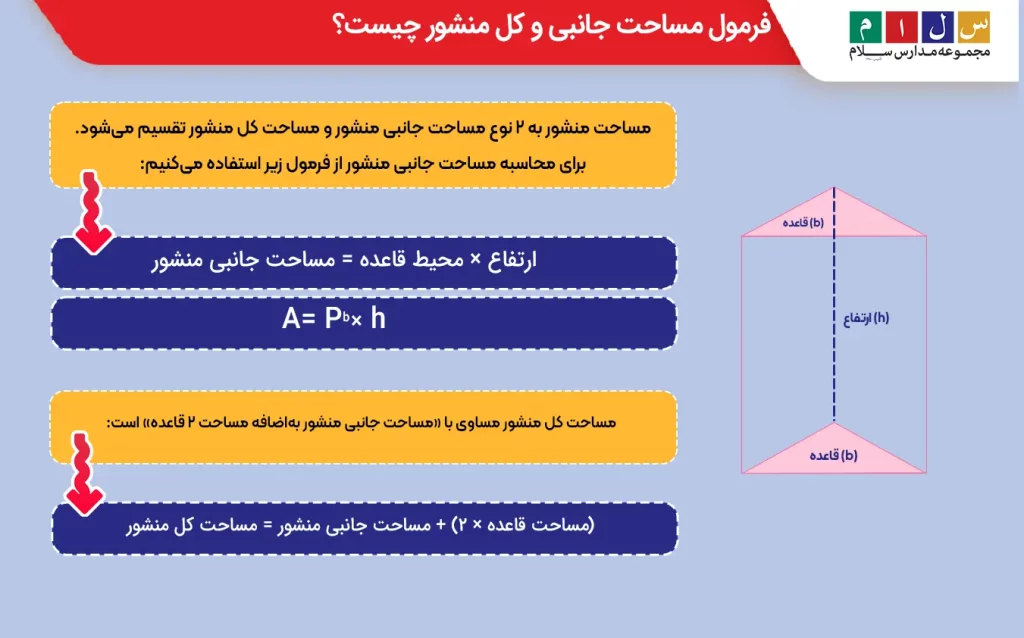
مساحت منشور به ۲ نوع مساحت جانبی منشور و مساحت کل منشور تقسیم میشود. برای محاسبه مساحت جانبی منشور از فرمول زیر استفاده میکنیم:
ارتفاع × محیط قاعده = مساحت جانبی منشور
یا
A = Pb × h
مساحت کل منشور مساوی با «مساحت جانبی منشور بهاضافه مساحت ۲ قاعده» است:
(مساحت قاعده × ۲) + مساحت جانبی منشور = مساحت کل منشور
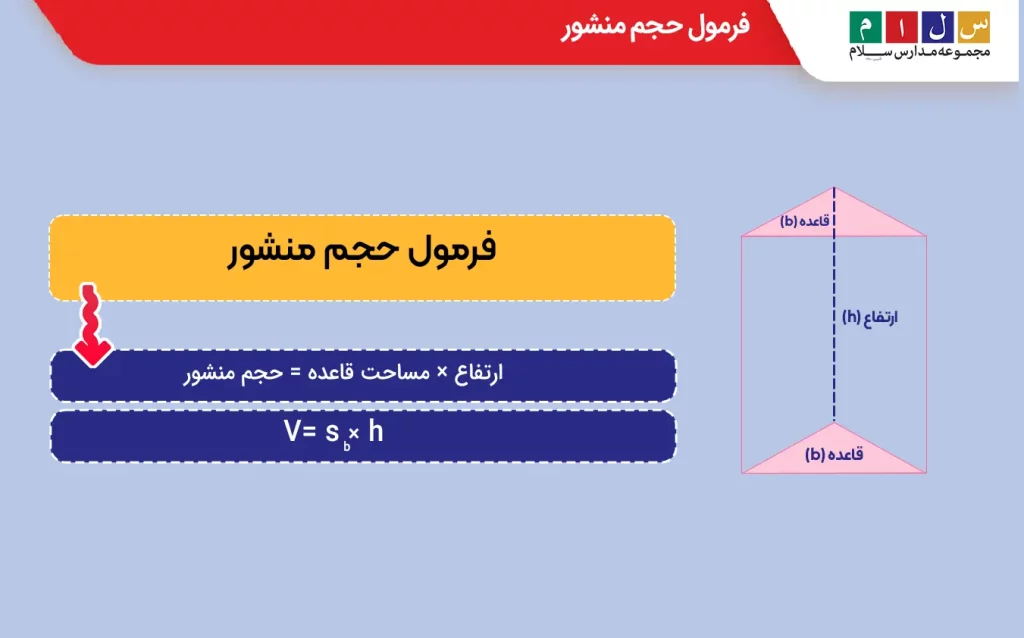
فرمول حجم منشور
ارتفاع × مساحت قاعده = حجم منشور
یا
V = Sb × h
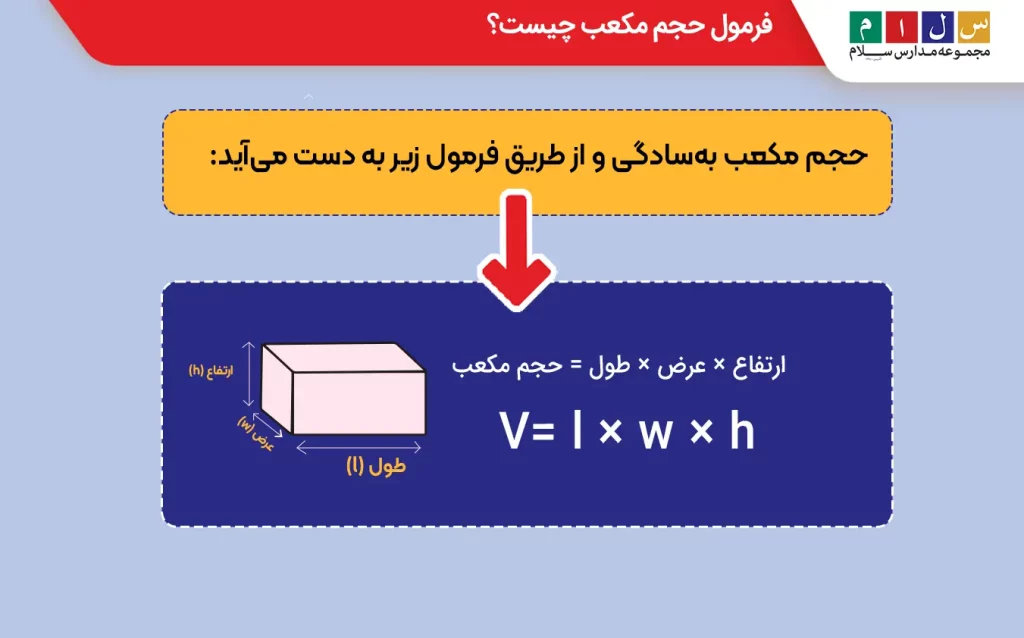
حجم مکعب
حجم مکعب بهسادگی و از طریق فرمول زیر به دست میآید:
ارتفاع × عرض × طول = حجم مکعب
یا
V = l × w × h
حجم هرم
حجم هرم را به این شکل محاسبه میکنیم:
(ارتفاع هرم × مساحت قاعده هرم) یکسوم = حجم هرم
یا

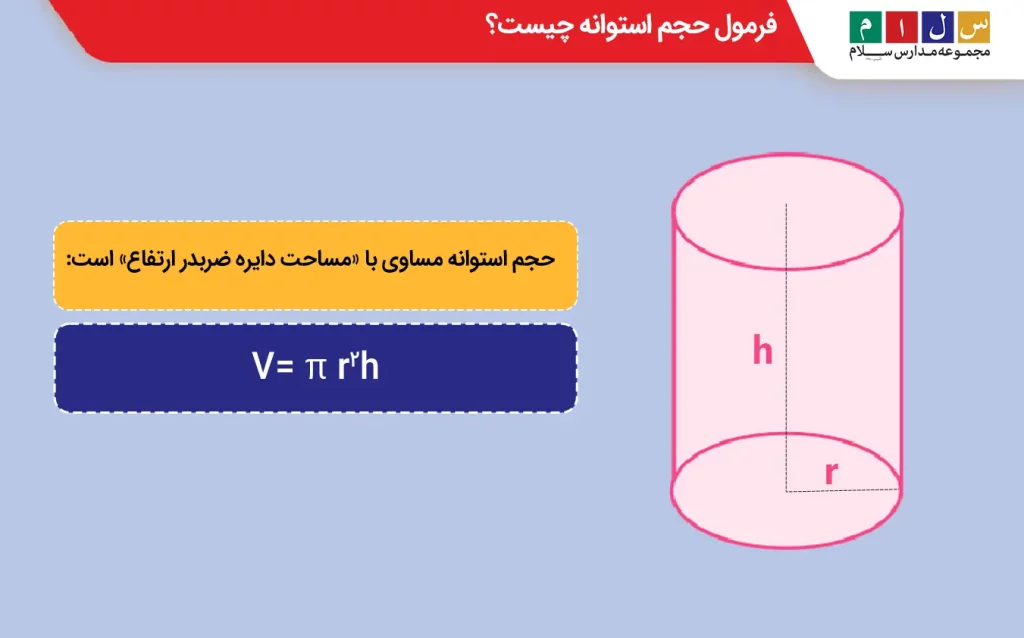
حجم استوانه
حجم استوانه مساوی با «مساحت دایره ضربدر ارتفاع» است:
ارتفاع × مساحت دایره = حجم استوانه
یا
V = πr۲h
جدول خلاصه مساحت و محیط اشکال هندسی
| شکل | محیط | مساحت |
| مجموع ۳ ضلع | قاعده × ارتفاع ÷ ۲ | |
 | یک ضلع × ۴ | یک ضلع × خودش |
 | ۲ × (طول + عرض) | طول × عرض |
 | مجموع ۴ ضلع | نصف مجموع قاعده اول و قاعده دوم × ارتفاع |
 | یک ضلع × ۴ | حاصلضرب قطرها ÷ ۲ |
 | جمع دو ضلع مجاور × ۲ | ارتفاع × قاعده |
 | ۲ × عدد پی × شعاع | عدد پی × شعاع به توان |
 | قطر + نصف محیط دایره | مساحت دایره ÷ ۲ |
 | یکچهارم محیط دایره + (شعاع × ۲) | یکچهارم مساحت دایره |
جدول خلاصه مساحت و حجم اشکال هندسی
| شکل | مساحت | حجم |
 | مساحت قاعده + مساحت وجههای جانبی | یکسوم (مساحت قاعده هرم × ارتفاع هرم) |
 | ۲ × {(طول × عرض) + (عرض × ارتفاع) + (طول × ارتفاع)} | طول × عرض × ارتفاع |
 | (مساحت دایره × ۲) + (۲ × محیط دایره × ارتفاع) | مساحت دایره × ارتفاع |
 | مساحت دایره × ۴ | چهارسوم عدد پی × شعاع بهتوان ۳ |
 | مساحت قاعده + مساحت وجه جانبی | یکسوم (مساحت قاعده × ارتفاع) |
 | مساحت جانبی منشور = محیط قاعده × ارتفاعمساحت کل منشور = مساحت جانبی منشور + (مساحت قاعده × ۲) | ارتفاع × مساحت قاعده |
سخن پایانی
فرمول محیط و مساحت انواع اشکال هندسی دوبعدی مانند مثلث و مربع و سهبعدی مانند استوانه و مخروط را در این مقاله بیان کردیم. علاوهبر این، ما در مقالههای جداگانهای با تمرینهای فراوان و مثالهای متنوع، محیط و مساحت و حجم هر کدام از این اشکال هندسی را بهزبان ساده توضیح دادهایم. برای مشاهده جزئیات بیشتر درباره محیط و مساحت هر کدام از شکلهای هندسی، روی لینک محیط، مساحت یا حجم آن شکل کلیک کنید.