فهرست مطالب
Toggleمثلثها اشکالی سهضلعی هستند که براساس طول اضلاع و اندازه زاویهها به انواع مختلفی دستهبندی میشوند. یکی از انواع مثلث که اندازه دو ضلع آن با هم برابر است مثلث متساوی الساقین نام دارد. در این آموزش قصد داریم ابتدا به معرفی این نوع مثلث بپردازیم و سپس درمورد خواص آن بیشتر توضیح دهیم.
مثلث متساوی الساقین چیست؟
مثلث شکلی هندسی است با سه ضلع و سه زاویه که مجموع زاویههای داخلی آن همیشه ۱۸۰ درجه است.
مثلث متساوی الساقین به مثلثی گفته میشود که دو ضلع با طول برابر دارد. اضلاع مساوی را «ساق» مثلث مینامند و به همین دلیل این نوع مثلث را مثلث متساوی الساقین میگویند.
مثلث متساوی الساقین از اجزای دیگری هم تشکیل شده است که عبارتاند از:
- قاعده: ضلع سوم مثلث که معمولاً اندازه آن با دو ضلع دیگر متفاوت است.
- زاویههای قاعده: زاویههای برابری که دو ساق مثلث با قاعده میسازند.
- زاویه رأس: زاویه بین دو ساق که مقابل قاعده قرار دارد و با زاویههای قاعده متفاوت است.
همانطور که میدانید، هر مثلثی ۳ ارتفاع داخلی دارد. در مثلث متساوی الساقین نیز همین تعداد ارتفاع وجود دارد اما جالب است بدانید که یکی از این ارتفاعها همانطور که در شکل زیر هم نشان داده شده است، قاعده را نصف میکند. بنابراین، این ارتفاع، خط تقارن، نیمساز و عمودمنصف مثلث نیز محسوب میشود.

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
انواع مثلث متساوی الساقین
مثلث متساوی الساقین براساس اندازه زاویه رأس به ۴ نوع دستهبندی میشود:
- مثلث متساوی الساقین حاده: مثلث متساویالساقینی که زاویه رأس آن کمتر از ۹۰ درجه است. در این نوع مثلث تمام زاویهها، زاویه حاده هستند.
- مثلث متساوی الساقین منفرجه: مثلث متساویالساقینی که زاویه رأس آن بیشتر از ۹۰ درجه یا زاویه منفرجه است.
- مثلث متساوی الساقین قائمالزاویه: مثلث متساویالساقینی که زاویه رأس آن برابر با ۹۰ درجه باشد.
- مثلث متساوی الساقین متساویالاضلاع: مثلث متساویالساقینی که تمام زاویههای آن ۶۰ درجه است.
در تصویر زیر میتوانید شکل این چهار نوع مثلث را مشاهده کنید.

اندازه زاویه های مثلث متساوی الساقین
در مثلث متساوی الساقین مانند هر مثلث دیگری سه زاویه وجود دارد که مجموع آنها برابر با ۱۸۰ درجه است. همانطور که گفتیم، در این نوع مثلث زاویههایی که مقابل ساقها قرار دارند و زاویه قاعده نامیده میشوند، با هم برابرند. این اطلاعات درمورد زاویههای مثلث متساوی الساقین میتواند در تعیین زاویههای مجهول به ما کمک کند.

مثال: زاویه قاعده یک مثلث متساوی الساقین ۸۰ درجه است. اندازه زاویه رأس این مثلث چند درجه است؟
جواب: با توجه به اینکه در مثلث متساوی الساقین دو زاویه قاعده یکسان وجود دارد و مجموع زوایای داخلی نیز ۱۸۰ درجه است داریم:
˚۱۸۰ = زاویه رأس + زاویه قاعده × ۲
˚۱۸۰ = زاویه رأس + ˚۸۰ × ۲
˚۱۸۰ = زاویه رأس + ˚۱۶۰
˚۲۰ =˚۱۶۰ – ˚۱۸۰ = زاویه رأس
خط تقارن مثلث متساوی الساقین
خط تقارن یا محور تقارن خطی فرضی است که اگر یک شکل را از آن قسمت تا کنیم دو نیمه یکسان ایجاد میشود. حال میخواهیم بررسی کنیم که یک مثلث متساوی الساقین چند محور تقارن دارد. مثلث متساوی الساقین بهدلیل داشتن دو ساق برابر تنها یک خط تقارن دارد. این خط تقارن همان ارتفاعی است که در بخشهای پیشین درمورد آن صحبت کردیم.
نکته: اگر در یک مثلث متساوی الساقین تمام اضلاع با هم برابر باشند، آنگاه مثلث سه خط تقارن خواهد داشت.

محیط مثلث متساوی الساقین
محیط یک شکل از اندازه دورتادور آن بهدست میآید. مطابق این تعریف، برای تعیین محیط مثلث متساوی الساقین باید اندازه دور این شکل را محاسبه کنیم یا بهعبارتی اندازه سه ضلع آن را با هم جمع بزنیم. ازآنجا که مثلث متساوی الساقین دو ساق برابر دارد، فرمول محیط آن بهصورت زیر خواهد بود:
قاعده + ساق × ۲ = محیط مثلث متساویالساقین

مثال: اگر طول ساق یک مثلث متساوی الساقین ۲۰ سانتیمتر و قاعده آن ۲۵ سانتیمتر باشد، محیط آن چقدر است؟
جواب: ازآنجا که مثلث متساوی الساقین دو ساق برابر دارد، خواهیم داشت:
قاعده + ساق × ۲ = محیط مثلث متساویالساقین
۶۵ سانتیمتر = ۲۵ + ۴۰ = ۲۵ + ۲۰ × ۲ = محیط مثلث متساویالساقین
مساحت مثلث متساوی الساقین
مساحت مثلث متساوی الساقین به اندازه سطحی گفته میشود که توسط سه ضلع آن احاطه شده است. مساحت این شکل هندسی از فرمول مساحت مثلث بهدست میآید:
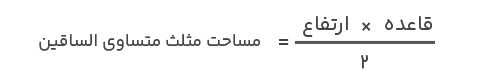
اگر قاعده مثلث متساوی الساقین را با b، ارتفاع آن را با h و مساحتش را با A نشان دهیم، فرمول مساحت را میتوان بهشکل زیر است.

اگر مقدار ارتفاع یعنی h مجهول باشد، میتوانیم با استفاده از قضیه فیثاغورس مقدار آن را مشخص کنیم. خواهیم داشت:
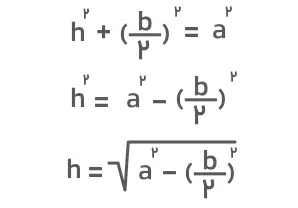
درنتیجه فرمول مساحت مثلث متساوی الساقین را میتوانیم بهصورت زیر بازنویسی کنیم:
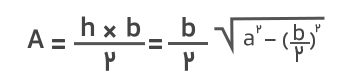
مثال: طول ساق یک مثلث متساوی الساقین ۷ سانتیمتر و قاعده آن ۴ سانتیمتر است. مساحت آن را محاسبه کنید.
جواب: مساحت مثلث مساوی است با حاصلضرب قاعده در ارتفاع تقسیم بر دو. در اینجا اندازه ارتفاع مجهول است و باید ابتدا با کمک قضیه فیثاغورس مقدار آن را بهصورت زیر بهدست آوریم:
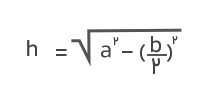
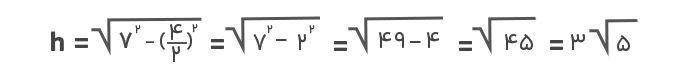
اکنون مقدار ارتفاع را در فرمول مساحت قرار میدهیم تا مساحت مثلث بهدست آید:
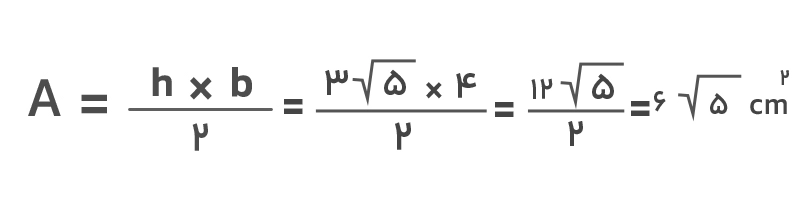
رسم مثلث متساوی الساقین
رسم این نوع مثلث بسیار ساده است و برای انجام آن تنها به یک پرگار، خطکش و مداد نیاز خواهید داشت. این ابزارها را آماده کرده و مراحل زیر را بهترتیب روی کاغذ اجرا کنید.
فرض کنید میخواهیم یک مثلث متساوی الساقین رسم کنیم که قاعده آن ۴ سانتیمتر و طول ساقهای آن ۶ سانتیمتر است. برای کشیدن این مثلث باید بهصورت زیر عمل کنیم:
- مرحله ۱: ابتدا قاعده مثلث را میکشیم. برای این کار با استفاده از خطکش یک خط راست به طول ۴ سانتیمتر رسم میکنیم و آن را (آ ب) مینامیم.
- مرحله ۲: دهانه پرگار را بهاندازه طول ساق یعنی ۶ سانتیمتر باز کرده و کمانی به مرکز (آ) میکشیم.
- مرحله ۳: بدون اینکه اندازه دهانه پرگار را تغییر دهیم، یک کمان دیگر این بار به مرکز (ب) رسم میکنیم.
- مرحله ۴: محل برخورد دو کمان را (ج) مینامیم و دو سر پارهخط (آ ب) را با خطکش به آن وصل میکنیم تا مثلث موردنظر رسم شود.

سخن پایانی
مثلث متساوی الساقین یکی از انواع مثلث است که دو ضلع برابر بهنام ساق و دو زاویه مساوی بهنام زاویه قاعده دارد. این مثلث انواع مختلفی دارد که در این مقاله آنها را معرفی کرده و تفاوت آنها را بیان کردیم. علاوهبر این فرمول محیط و مساحت مثلث متساوی الساقین و نحوه محاسبه آنها را همراه با مثال توضیح دادیم. بهطور کلی، ویژگی بارزی که این مثلث را از سایر مثلثها متمایز میکند، مساوی بودن دو ضلع از سه ضلع آن است که معمولاً در نگاه اول میتوان آن را تشخیص داد.
سؤالات متداول
- مثلث متساوی الساقین چیست؟
مثلثی که دو ضلع مساوی داشته باشد را مثلث متساوی الساقین میگویند. - مثلث متساوی الساقین چند خط تقارن دارد؟
مثلث متساوی الساقین یک خط تقارن دارد. - فرمول محیط مثلث متساوی الساقین چیست؟
محیط مثلث متساوی الساقین برابر است با مجموع اضلاع آن. - فرمول مساحت مثلث متساوی الساقین چیست؟
مساحت مثلث متساوی الساقین مساوی است با «حاصلضرب قاعده در ارتفاع تقسیم بر دو».










36 پاسخ
یعنی هر مثلثی که دو ضلعش مساویه هم، حتما مثلث متساوی الساقین است؟
با سلام دقیقاً همینطور است. اگر دو ضلع از ضلعهای مثلث با هم برابر باشند، آن مثلث متساوی الساقین تلقی میشود.
خیلی ممنون ازتون مقالهتون درباره مثلث متساوی الساقین واقعاً کمک کرد تا بفهمم «پایه»، «زاویه رأس» و بقیه بخشها یعنی چی
با سلام خیلی ممنونیم از لطف شما؛ خوشحیالم که ساختار و قسمتهای هندسی برایتان شفاف شده است. امیدوارم در مباحث بعدی نیز همراهتان باشیم.
خیلی باحاله ممنون که اینقدر ساده توضیح دادین درباره مثلث متساوی الساقین مرسی از زحمتی که کشیدین
با سلام از محبت شما سپاسگزارم.
یعنی اگه من یه برگه کاغذ تا بزنم و یه مثلث بکشم بعد اگه ببینم دو ضلعش مساویه میشه فهمید اون یه مثلث متساوی الساقین است؟
با سلام درست است. هرگاه در مثلثی دو ضلع مساوی باشند، آن مثلث متساوی الساقین است بینیاز از قیاس با چیز دیگر.
همیشه مثلث متساوی الساقین شکلش قرینهست؟ یعنی اگه اون ضلع قاعده رو وسط تا بزنیم، دو نیمه دقیقاً مثل هماند؟
با سلام بله یکی از ویژگیهای مهم مثلث متساوی الساقین همین تقارن است: ارتفاع از رأس به قاعده، مثل محور تقارن عمل میکند و مثلث را به دو قسمت برابر تقسیم میکند.
سلام یه سوال داشتم اون دو زاویه روبهروِ اضلاع مساوی هم همیشه با هم مساویان؟
با سلام بله؛ یکی از خواص مهم مثلث متساوی الساقین همین است: اگر دو ضلع مساوی باشند، زوایای مقابل آن اضلاع نیز برابراند.
خیلی ممنون بابت مقالهتون کمک بزرگی بود! خواستم بگم واقعاً توضیحاتتون درباره مثلث متساوی الساقین واضح و مفید بودن
سپاس فراوان از لطف شما؛ خوشحیالم که این توضیحات برایتان مفید بوده.
اون مثلثی که دو تا ضلعش با هم برابر باشن یعنی دقیقاً اون که شما اسمش گذاشتین مثلث متساوی الساقین، درسته؟
با سلام بله؛ مثلث متساوی الساقین، مثلثی است که دو ضلعش با هم برابراند. همین ویژگی باعث میشود دو زاویه روبهروی آن اضلاع نیز مساوی شوند.
سلام خیلی ممنونم از مقاله عالیتون واقعا کامل بود
سلام، خواهش میکنم.
خوشحیالم که مقاله برای شما کامل و مفید بوده.
سلام وقتتون بخیر باشه
اگه اون ضلع سوم هم مساوی باشه یعنی هر سه ضلع برابر باشن اونم باز مثلث متساوی الساقین حساب میشه؟
با سلام بله. در تعاریف امروزی، اگر حداقل دو ضلع برابر باشند، مثلث متساوی الساقین گفته میشود، بنابراین مثلثی با سه ضلع برابر (یعنی متساویالاضلاع) هم زیرمجموعه مثلث متساوی الساقین اس
سلام وقت بخیر
خیلی ممنونم از مقاله مفیدتون
با سلام خواهش میکنم، خوشحالم که توضیحات براتون ساده و قابل فهم بوده.
مرسی از مقالهتون! توضیحات بهقدری روان بود که فهم ویژگیهاش برام خیلی راحت شد
با سلام سپاس از لطف و توجه شما!
سوال وقت بخیر یه سوال داشتم وقتی دو ضلع برابر باعث میشه زاویههای مقابلشون هم برابر بشن؟
وقتی دو ضلع یک مثلث برابر باشند، توازن طبیعی هندسه مشخص میشود و به همین دلیل زاویههای مقابل این دو ضلع نیز با هم برابر خواهند بود.
اگه یه مثلث سه ضلع برابر داشته باشه، باز هم میتونیم بگیم متساویالساقینه؟ چه فرقی با متساویالاضلاع داره؟
با سلام مثلثی که سه ضلعش برابر باشد، دیگر تنها متساویالساقین نیست؛ این همان مثلث متساویالاضلاع است هر سه زاویهاش برابر و هر خطی که از رأسها به وسط ضلع مقابل کشیده شود، محور تقارن خواهد بود.
سلام وقت بخیر یه سوال داشتم مثلث متساویالساقین همیشه تقارن داره؟
با سلام بله، قطعاً! یکی از وجوه بارز این مثلث آن است که یک خط تقارن دارد که از رأس مقابل قاعده تا وسط آن کشیده میشود و شکل را به دو نیمۀ برابر تقسیم میکند؛ این همان جلوهی هنرمندانهی نظم در هندسه است.
خیلی ممنون که با مثال و تعریف ساده، مثلث متساوی الساقین رو توضیح دادین دیدم مسالهها سادهتر شدن برام
با سلام خواهش میکنم، خوشحالم که توضیحات باعث سادهتر شدن مسائل برای شما شده است.
موفق باشید.
واقعا ممنون! اون بخش فرمول مساحت و محیطش عالی بود
با سلام خواهش میکنم، خوشحالم که مفید بوده است.از لطف و بازخورد ارزشمند شما سپاسگزارم.
سلام وقت بخیر خیلی عالی بود فرمول محیط مثلث متساوی الساقین ساده اش چی میشه ؟
با سلام محیط مثلث متساویالساقین برابر است با مجموع طول سه ضلع آن.چون دو ضلع با هم برابرند، فرمول محیط برابر است با ۲ × طول ساق + طول قاعده.