مرکز تقارن چیست؟ | تعریف + اشکال دارای مرکز تقارن

اگر به گل‌ها و طرح‌های روی فرش‌ها دقت کرده باشید، می‌بینید که هر کدام از آن‌ها در نیمه دیگر فرش هم تکرار شده‌اند، به‌گونه‌ای که به‌نظر می‌رسد نسبت به مرکز فرش نیم‌دور چرخیده‌اند. درواقع، فرش یکی از نمونه‌های رایج تقارن مرکزی در دنیای اطراف ماست. در طبیعت هم نمونه‌های زیادی از این نوع تقارن مشاهده می‌شود، مانند برگ‌ها، گل‌های رنگارنگ و نقش روی بدن حیوانات.

برای اینکه بتوانید به سوالاتی مانند تقارن مرکزی و مرکز تقارن چیست در اشکال هندسی و اجسام پیرامون خود به‌راحتی پاسخ دهید، پیشنهاد می‌کنیم این مقاله را دنبال کنید. به موضوعاتی که در مطلب تفاوت و شباهت اشکال هندسی اشاره شد هم سری بزنید.

مرکز تقارن چیست؟

نقطه‌ای که یک شکل نسبت به آن تقارن مرکزی دارد را مرکز تقارن می‌گویند. به‌عبارت دیگر، مرکز تقارن همان نقطه‌ای است که اگر شکل را حول آن به‌اندازه نیم‌دور بچرخانیم، به حالت اولیه‌اش برمی‌گردد و روی خودش منطبق می‌شود.

تقارن مرکزی چیست؟

اگر بتوان یک شکل را به دو نیمه یکسان و مشابه تقسیم کرد، طوری که یک نیمه قرینه و بازتاب نیمه دیگر باشد یعنی اگر از یک خط فرضی آن را تا کنیم، دو قسمت دقیقاً روی هم بیفتند، آن شکل را دارای تقارن یا متقارن می‌نامند، در غیر این‌صورت، به آن شکل نامتقارن می‌گویند.

به‌عنوان مثال، در تصویر زیر، شکل سمت راست متقارن است چون می‌توان از وسط (خط فرضی) آن را به دو قسمت مشابه و مساوی تقسیم کرد، اما در شکل سمت چپ این کار امکان‌پذیر نیست.

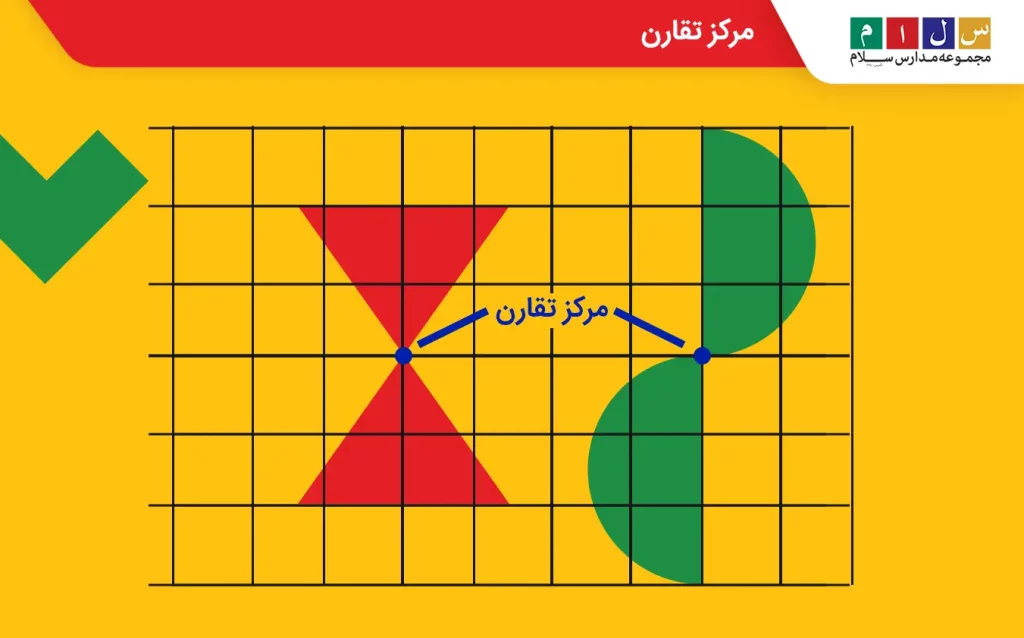
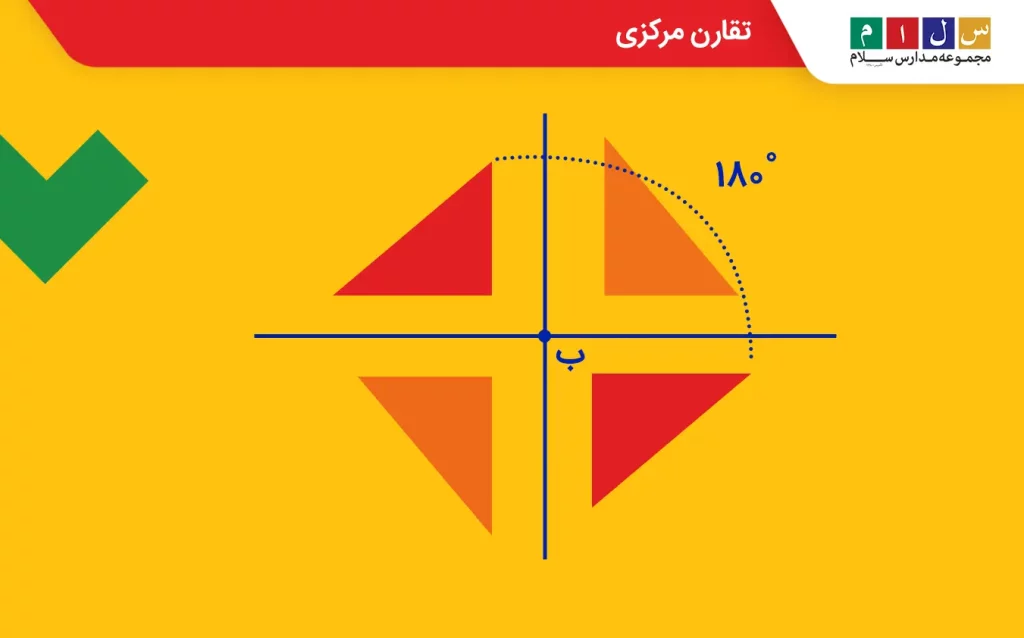
تقارن مرکزی یکی از انواع تقارن است و به این معناست که اگر یک شکل را به‌اندازه نیم‌دور (۱۸۰ درجه) حول نقطه‌ای (مرکز) بچرخانیم، طوری که پس از چرخش، شکل روی خودش منطبق شود، می‌گوییم شکل تقارن مرکزی یا تقارن نقطه‌ای دارد.

در تصویر زیر، تقارن مرکزی یک مثلث حول نقطه ب نشان داده شده است.

تفاوت مرکز تقارن و تقارن مرکزی در چیست؟

مرکز تقارن و تقارن مرکزی دو مفهوم مرتبط با هم هستند، اما یکسان نیستند. مرکز تقارن یک نقطه در شکل است که اگر هر نقطه‌ای از شکل را نسبت به آن قرینه کنیم، نقطه‌ی جدید دوباره روی خود شکل قرار می‌گیرد. 

مثلاً در دایره، مرکز دایره مرکز تقارن آن است. اگر نقطه‌ای از محیط دایره را نسبت به مرکز قرینه کنیم، نقطه‌ی قرینه در سمت مقابل روی محیط دایره قرار می‌گیرد. 

یعنی مرکز تقارن نقطه ای است که قرینه هر نقطه از شکل نسبت به آن بر خود شکل منطبق می شود. 

اما تقارن مرکزی به وجود یک نقطه مرکزی اشاره دارد که شیء را به چند بخش تقسیم می‌کند، به طوری که هر بخش نسبت به نقطه مرکزی تقارن، تقارن متقابل دارد.

پیشنهاد مطالعه: دایره چند شعاع دارد؟

چگونه تقارن مرکزی یک شکل را تشخیص دهیم؟

برای اینکه بررسی کنیم آیا یک شکل تقارن مرکزی دارد یا خیر، دو راه وجود دارد:

راه‌حل اول: شکل را به‌اندازه ۱۸۰ درجه بچرخانید. اگر شکل پس از چرخش مشابه و قرینه شکل اصلی بود و روی خودش منطبق شد، یعنی شکل موردنظر تقارن مرکزی دارد.

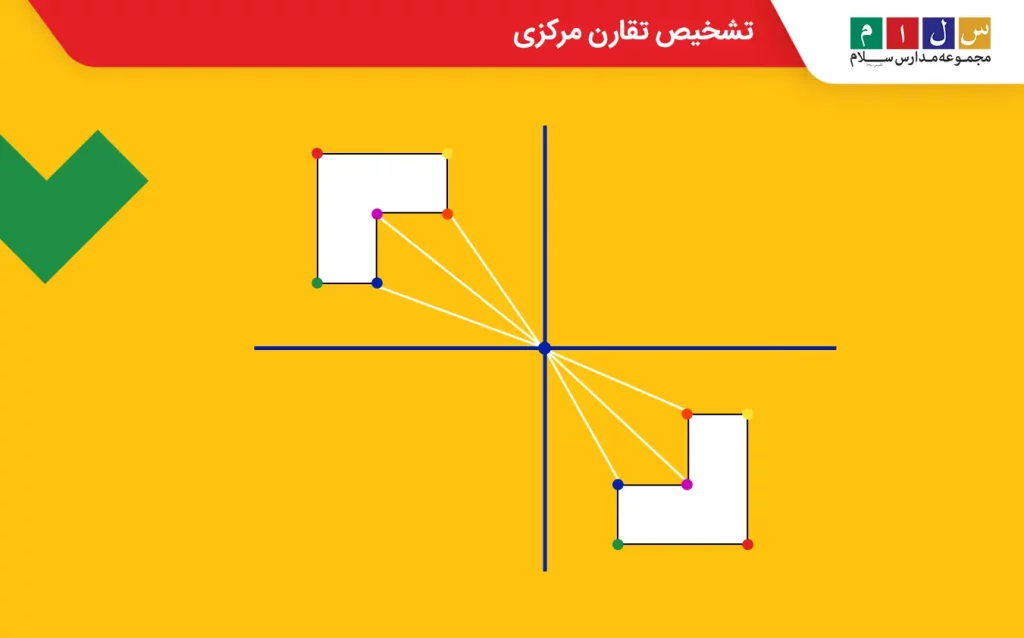
راه‌حل دوم: کافی‌ست نقاط مختلفی از شکل را درنظر بگیرید و  از آن نقاط تا مرکز یک خط رسم کنید سپس، خط را به همان اندازه تا مرکز امتداد دهید. اگر همان نقاط از شکل در طرف مقابل با همان فاصله از مرکز وجود داشت، شکل تقارن مرکزی دارد. مثلاً  در شکل زیر، فاصله هر دو نقطه هم‌رنگ تا مرکز با هم برابر است. این نشان می‌دهد که شکل زیر تقارن مرکزی دارد.

مرکز تقارن اشکال هندسی

در این قسمت، تقارن مرکزی انواع اشکال هندسی را بررسی کرده و مشخص می‌کنیم که هر کدام خط تقارن مرکزی دارند یا خیر. دقت داشته باشید، وقتی که می‌گوییم یک شکل هندسی مرکز تقارن دارد، منظور این است که شکل پس از چرخیدن به‌اندازه ۱۸۰ درجه حول مرکزش، روی خودش منطبق می‌شود.

مرکز تقارن متوازی الاضلاع

محل برخورد قطرهای متوازی‌الاضلاع مرکز تقارن این شکل هندسی است.

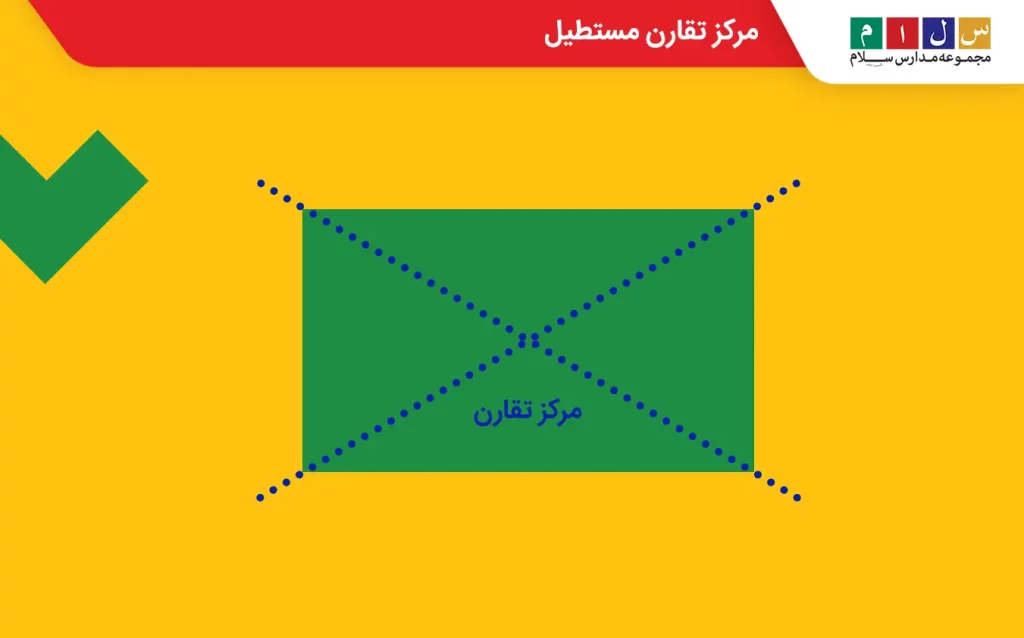
مرکز تقارن مستطیل

محل برخورد قطرهای مستطیل، همان مرکز تقارن است.

مرکز تقارن لوزی

محل برخورد قطرهای بزرگ و کوچک لوزی مرکز تقارن آن است.

مرکز تقارن ذوزنقه

هیچ‌کدام از انواع ذوزنقه مرکز تقارن ندارند.

مرکز تقارن چندضلعی منتظم

اگر تعداد اضلاع چندضلعی منتظم زوج باشد، چندضلعی مرکز تقارن دارد، اما اگر تعداد اضلاع آن فرد باشد، چندضلعی پس از دوران به حالت اولیه برنمی‌گردد و درنتیجه تقارن مرکزی و مرکز تقارن ندارد.

مرکز تقارن مربع

محل برخورد قطرهای مربع مرکز تقارن است.

مرکز تقارن دایره

مرکز تقارن دایره، همان مرکز دایره یا به‌عبارتی، محل برخورد قطرهای آن است.

پیشنهاد مطالعه: قطر چیست؟

مرکز تقارن بیضی

محل برخورد قطرهای بزرگ و کوچک بیضی مرکز تقارن آن است. اگر بیضی را نسبت به مرکزش ۱۸۰ درجه بچرخانیم شکل روی خودش منطبق می‌شود.

مرکز تقارن مثلث

هیچ‌کدام از انواع مثلث مرکز تقارن ندارند، چون پس از چرخش۱۸۰ درجه روی خودشان منطبق نمی‌شوند و به حالت اولیه برنمی‌گردند. در تصویر زیر، به‌عنوان نمونه تقارن مرکزی مثلث متساوی‌الاضلاع را بررسی کرده‌ایم.

مرکز تقارن ستاره

ستاره‌هایی که تعداد رأس آن‌ها فرد است، دارای مرکز تقارن نیستند، اما آن‌هایی که تعداد رأسشان زوج است، تقارن مرکزی و درنتیجه مرکز تقارن دارند. برای مثال، ستاره پنج‌رأس پس از دوران به حالت اولیه برنمی‌گردد و تقارن مرکزی ندارد،  اما ستاره چهاررأس پس از چرخش، روی خودش منطبق می‌شود و نسبت به مرکزش متقارن است.

تفاوت محور تقارن و مرکز تقارن چیست؟

محور تقارن خطی است که یک شکل را به دو نیمه مشابه تقسیم می‌کند، به‌گونه‌ای که هر دو نیمه قرینه هم باشند و بر هم منطبق شوند اما مرکز تقارن به نقطه‌ای گفته می‌شود که یک شکل پس از دوران ۱۸۰ درجه حول آن روی خودش منطبق می‌شود. در شکل زیر می‌توانید تفاوت این دو را مشاهده کنید.

بررسی وجود مرکز تقارن در نقطه، خط، نیم خط و پاره خط

در این بخش، بررسی می‌کنیم که آیا در نقطه، خط، نیم‌خط و پاره‌خط مرکز تقارن وجود دارد یا نه. 

• نقطه: یک نقطه تنها یک مرکز تقارن دارد و آن خود نقطه است. در واقع، هر نقطه در فضا می‌تواند به‌عنوان مرکز تقارن خودش در نظر گرفته شود.
• خط: با توجه به اینکه دو طرف یک خط تا بی‌نهایت ادامه دارد، نمی‌توان درمورد مرکز تقارن آن نظری داد.
• نیم‌خط: یک نیم‌خط هیچ خط تقارنی ندارد زیرا نیم‌خط فقط از یک طرف امتداد دارد و اگر آن را حول هر نقطه‌ای روی خودش، بچرخانیم، نمی‌تواند به‌طور کامل روی خودش منطبق شود
• پاره‌خط: پاره‌خط تنها یک مرکز تقارن دارد و آن نقطه وسط پاره‌خط است. اگر پاره‌خط را حول این نقطه به‌اندازه ۱۸۰ درجه بچرخانیم، پاره‌خط دقیقاً روی خودش منطبق خواهد شد. در حقیقت، پس از دوران یک پاره‌خط اگرچه دو سر آن جایشان عوض می‌شود اما درنهایت به حالت اولیه خود باز خواهد گشت.

پیشنهاد مطالعه: تعریف نیم خط، خط و پاره خط چیست؟

جدول مرکز تقارن

در ادامه، جدول مرکز تقارن آورده شده است.

شکل	مرکز تقارن	محور تقارن	محل برخورد قطرها، مرکز تقارن است	قطر، محور تقارن است	تقارن چرخشی
مربع	دارد	۴	بله	بله	دارد
مستطیل	دارد	۲	بله	خیر	دارد
لوزی	دارد	۲	بله	بله	دارد
متوازی‌الاضلاع	دارد	صفر	بله	خیر	دارد
مثلث	ندارد	۳	خیر	خیر	دارد
مثلث متساوی‌الاضلاع	ندارد	۳	خیر	خیر	دارد
مثلث	ندارد	۱	خیر	خیر	ندارد
مثلث متساوی‌الساقین	ندارد	۱	خیر	خیر	ندارد
مثلث مختلف‌الاضلاع	ندارد	صفر	خیر	خیر	ندارد
ذوزنقه	ندارد	صفر	خیر	خیر	ندارد
متوازی‌الاضلاع مختلف‌الاضلاع	ندارد	صفر	خیر	خیر	ندارد
دایره	دارد	بیشمار	بله	بله	دارد
بیضی	دارد	۲	بله	بله	دارد
نیم‌دایره	ندارد	۱	خیر	خیر	ندارد
ربع‌دایره	ندارد	۱	خیر	خیر	ندارد

سخن پایانی

اگر یک شکل را نیم‌دور (۱۸۰ درجه) حول نقطه‌ای دوران دهیم، طوری که پس از چرخش روی شکل اولیه‌اش منطبق شود، آن شکل دارای تقارن مرکزی یا نقطه‌ای خواهد بود.. نقطه‌ای که شکل حول آن می‌چرخد و نسبت به آن تقارن مرکزی دارد را مرکز تقارن می‌گویند. برای اینکه مشخص کنیم یک شکل تقارن مرکزی دارد یا نه، دو راه وجود دارد:
۱) اینکه شکل را نیم‌دور دوران دهیم، اگر شکل روی خودش منطبق شد، پس شکل موردنظر تقارن مرکزی دارد، در غیر این‌صورت شکل دارای تقارن مرکزی نیست.
۲) اینکه نقاط مشابه دو شکل را به مرکز وصل کنیم، اگر فاصله هر دو نقطه تا مرکز برابر بود و دو شکل قرینه هم بودند، شکل موردنظر تقارن مرکزی خواهد داشت. بسیاری از اشکال هندسی شناخته‌شده نیز دارای تقارن مرکزی و درنتیجه مرکز تقارن هستند، ازجمله دایره، بیضی، مربع، مستطیل، لوزی، متوازی‌الاضلاع و چندضلعی‌های منتظمی که تعداد اضلاعشان زوج است.

سؤالات متداول

1. چگونه تقارن مرکزی یک شکل را تشخیص دهیم؟
   برای مشخص کردن تقارن مرکزی یک شکل دو روش وجود دارد:
   ۱) شکل را به‌اندازه ۱۸۰ درجه بچرخانیم. اگر شکل پس از چرخش مشابه و قرینه شکل اصلی بود و روی خودش منطبق شد یعنی شکل موردنظر تقارن مرکزی دارد.
   ۲) نقاط مختلفی از شکل را با رسم خط به مرکز وصل کنیم و به‌همان اندازه، خط را تا نقاط مشابه آن‌ها امتداد دهیم، اگر فاصله نقاط مشابه تا مرکز برابر باشد، شکل موردنظر دارای تقارن مرکزی است.
2. مرکز تقارن چیست؟
   نقطه‌ای است که شکل پس از دوران ۱۸۰ درجه حول آن، به حالت اولیه‌اش برمی‌گردد و روی خودش منطبق می‌شود.
3. تفاوت مرکز تقارن و تقارن مرکزی چیست؟
   مرکز تقارن نقطه‌ای است که شکل پس از دوران ۱۸۰ درجه حول آن، به حالت اولیه‌اش برمی‌گردد. تقارن نسبت به این نقطه را تقارن مرکزی می‌گویند.
4. کدام شکل مرکز تقارن ندارد؟
   شکل‌هایی که پس از دوران ۱۸۰ درجه روی خودشان منطبق نمی‌شوند، مرکز تقارن ندارند، ازجمله مثلث، ذوزنقه، چندضلعی‌های منتظم با تعداد ضلع فرد و ستاره‌هایی که تعداد رأس آن‌ها فرد است.
5. چه شکل‌هایی مرکز تقارن دارند؟
   شکل‌هایی که پس از دوران ۱۸۰ درجه روی خودشان منطبق می‌شوند، مرکز تقارن دارند، مانند دایره، بیضی، متوازی‌الاضلاع، مربع، مستطیل، لوزی، چندضلعی‌های منتظم با تعداد ضلع زوج و ستاره‌هایی که تعداد رأس زوج دارند.
6. آیا متوازی‌الاضلاع مرکز تقارن دارد؟
   بله. محل برخورد قطرهای متوازی‌الاضلاع مرکز تقارن آن است.
7. آیا مثلث مرکز تقارن دارد؟
   هیچ‌کدام از انواع مثلث مرکز تقارن ندارند.
8. آیا لوزی مرکز تقارن دارد؟
   بله. مرکز تقارن لوزی در محل برخورد قطرهای آن قرار دارد.
9. آیا ذوزنقه مرکز تقارن دارد؟
   خیر. هیچ‌کدام از انواع ذوزنقه مرکز تقارن ندارند.
10. آیا دایره مرکز تقارن دارد؟
    بله. مرکز تقارن دایره در مرکز آن قرار دارد.
11. آیا بیضی مرکز تقارن دارد؟
    بله. محل برخورد قطرهای بزرگ و کوچک بیضی مرکز تقارن آن است.
12. کدام حرف‌های انگلیسی مرکز تقارن دارند؟
    از میان حروف انگلیسی تنها حروف H، I، N، O، S، X و Z مرکز تقارن دارند.