عمود منصف چیست؟ ׀ نحوه رسم عمود منصف + حل مثال های کاربردی

در این مقاله می‌‌خواهیم ابتدا درمورد مفهوم عمود منصف صحبت کنیم و توضیح دهیم که عمود منصف چیست. سپس، نحوه رسم کردن عمود منصف و ویژگی‌‌های آن را بیان کنیم. در آخر نیز با قضیه عمود منصف آشنا خواهیم شد و برای درک بهتر این مفهوم هندسی به حل چند مثال خواهیم پرداخت. 

عمود منصف چیست؟

اگر خطی عمود بر یک پاره‌‌خط رسم کنیم طوری‌‌که خط عمود به نقطه وسط پاره‌‌خط برخورد کند، آن خط را عمود منصف می‌‌نامیم.

عمود منصف خطی است که یک پاره‌‌خط را به دو قسمت مساوی تقسیم می‌‌کند و در نقطه تقاطع زاویه ۹۰ درجه می‌‌سازد. به‌‌بیان دیگر، عمود منصف همان‌‌طور که از نامش پیداست به خط عمودی گفته می‌‌شود که یک پاره‌‌خط را نصف می‌‌کند. برای مثال، در شکل زیر خط CE، پاره‌‌خط AB را نصف کرده و بر آن عمود است. درنتیجه خط CE عمود منصف پاره‌‌خط AB محسوب می‌‌شود.

ویژگی های عمود منصف

حالا که با مفهوم هندسی عمود منصف آشنا شدیم، به بررسی ویژگی عمود منصف می‌‌پردازیم. این ویژگی‌‌ها در ادامه آورده شده‌‌اند:

• عمود منصف با پاره‌‌خطی که آن را نصف می‌‌کند زاویه راست درجه می‌‌سازد.
• عمود منصف پاره‌‌خط را دقیقاً در نقطه وسط آن قطع می‌‌کند.
• هر نقطه از عمود منصف از دو سر پاره‌‌خطی که بر آن عمود شده است فاصله یکسانی دارد.
• برای هر پاره‌‌خط تنها می‌‌توان یک عمود منصف رسم کرد.

رسم عمود منصف پاره خط

عمود منصف یک پاره‌‌خط را می‌‌توان با استفاده از خط‌‌کش و  پرگار به‌‌راحتی رسم کرد. این وسایل را آماده کنید و مراحل زیر را به‌‌ترتیب انجام دهید تا عمود منصف پاره‌‌خط رسم شود:

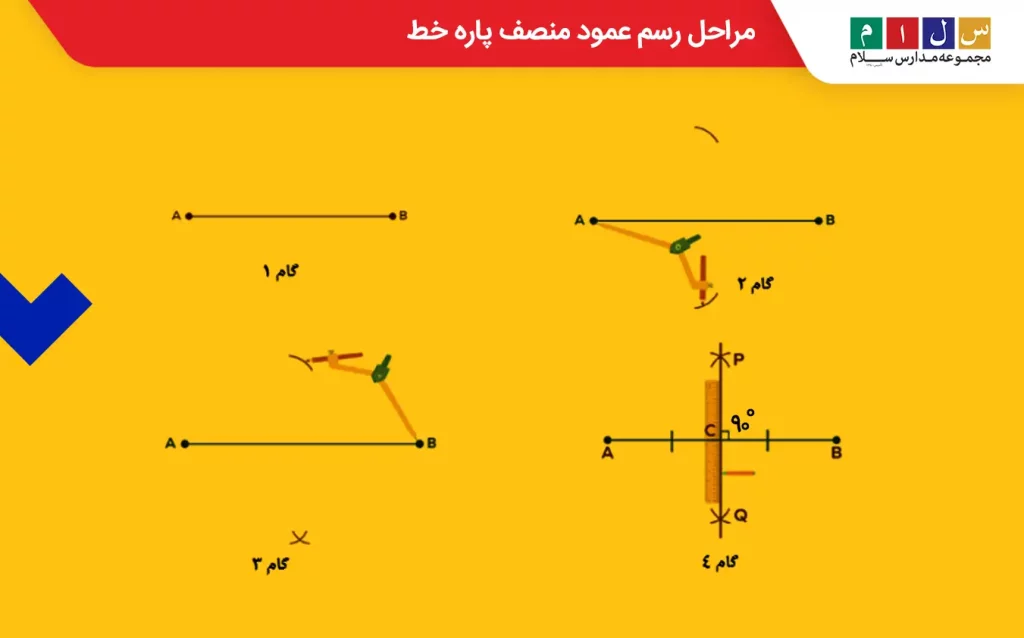
• گام ۱: پاره‌‌خط AB را مانند شکل زیر رسم کنید.
• گام ۲: دهانه پرگار را اندکی بیشتر از نصف طول پاره‌‌خط باز کنید. سوزن پرگار را روی نقطه A قرار دهید و دو کمان در پایین و بالای پاره‌‌خط رسم کنید.
• گام ۳: حالا بدون اینکه اندازه دهانه پرگار را تغییر دهید، سوزن پرگار را در نقطه B قرار داده و مانند مرحله قبل، دو کمان در پایین و بالای پاره‌‌خط بکشید.
• گام ۴: محل برخورد دو کمان در بالا و پایین پاره‌‌خط یعنی P و Q را با استفاده از خط‌‌کش به هم وصل کنید. خط PQ عمود منصف پاره‌‌خط AB است و در نقطه C این پاره‌‌خط را قطع می‌‌کند. درنتیجه AC = BC است.

عمود منصف مثلث

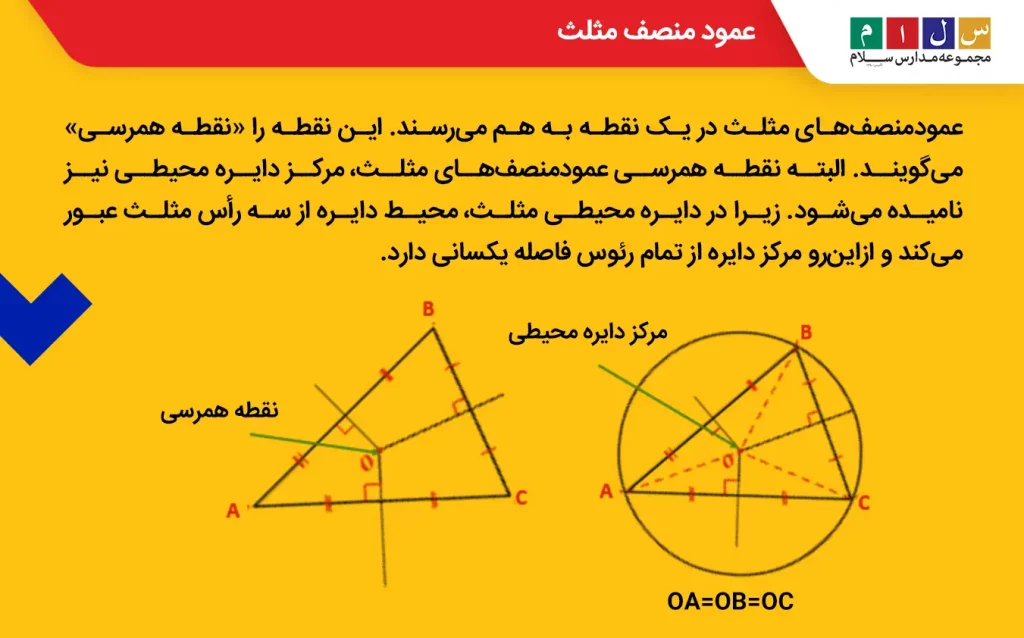
یک مثلث از سه ضلع (پاره‌‌خط) ساخته شده است و برای هر یک از سه ضلع آن می‌‌توانیم یک عمود منصف رسم کنیم. بنابراین، مثلث سه عمود منصف خواهد داشت. در شکل زیر عمودمنصف‌‌های یک مثلث مختلف‌‌الاضلاع نشان داده شده است.

عمودمنصف‌‌های مثلث در یک نقطه به هم می‌‌رسند. این نقطه را «نقطه همرسی» می‌‌گویند. البته نقطه همرسی عمودمنصف‌‌های مثلث، مرکز دایره محیطی نیز نامیده می‌‌شود. زیرا در دایره محیطی مثلث، محیط دایره از سه رأس مثلث عبور می‌‌کند و از این‌‌ رو مرکز دایره از تمام رئوس فاصله یکسانی دارد. تصویر زیر این موضوع را به‌‌خوبی نشان می‌‌دهد.

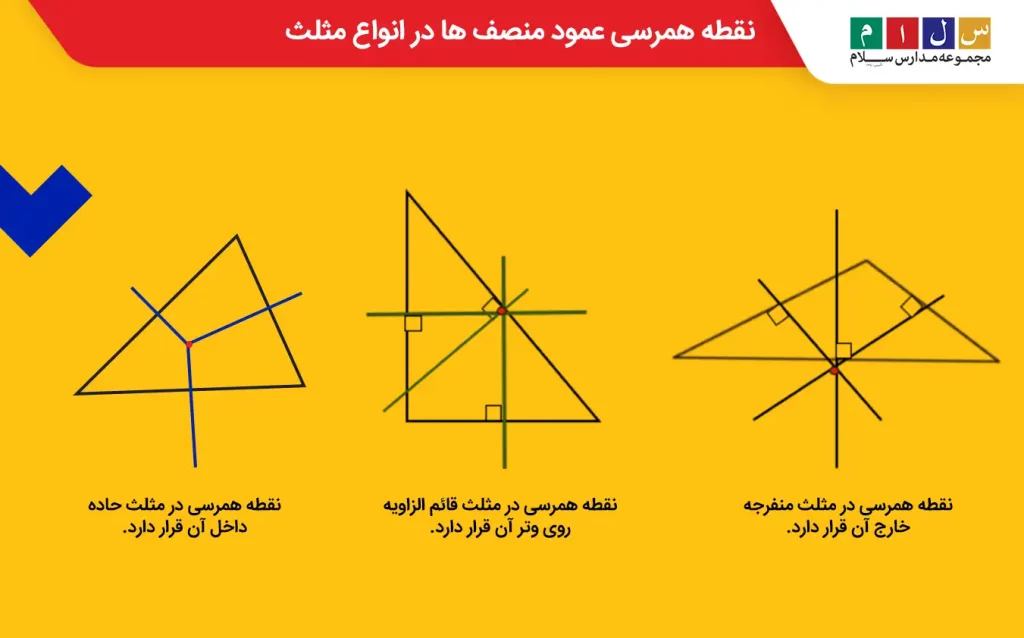
محل قرار گرفتن نقطه همرسی عمودمنصف‌‌های یک مثلث بستگی به نوع مثلث دارد. نقطه همرسی و درنتیجه مرکز دایره محیطی در مثلث حاده، داخل آن در مثلث منفرجه، خارج از آن و در مثلث قائم‌‌الزاویه روی وتر قرار می‌‌گیرد. در شکل زیر، نقطه همرسی عمود منصف مثلث قائم الزاویه و مثلث حاده و منفرجه نشان داده شده است.

رسم عمود منصف مثلث

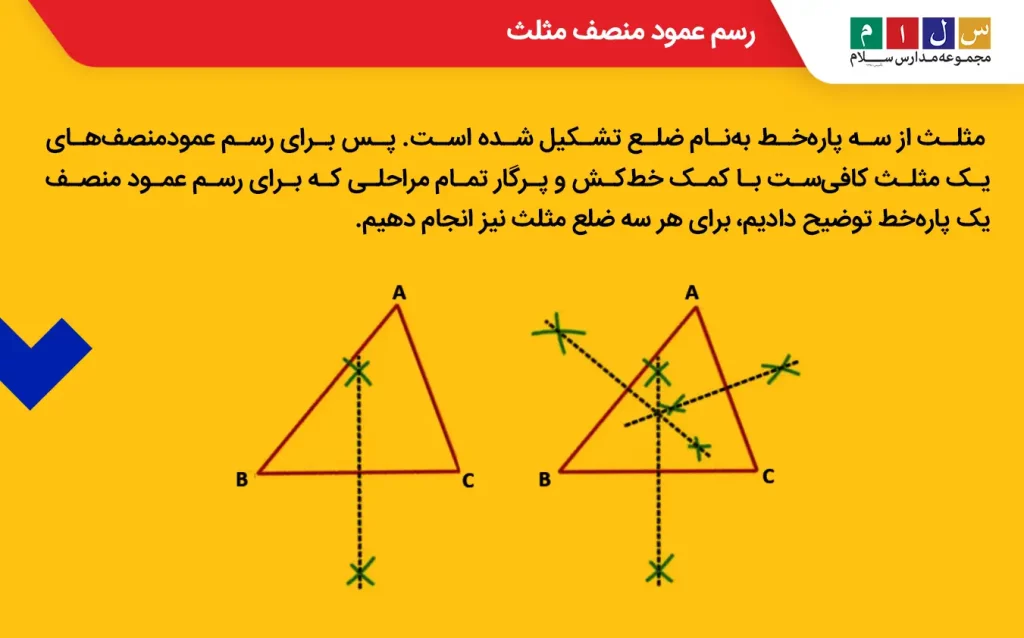
همان‌‌طور که گفتیم، مثلث از سه پاره‌‌خط به‌‌نام ضلع تشکیل شده است. پس برای رسم عمودمنصف‌‌های یک مثلث کافی‌‌ست با کمک خط‌‌کش و پرگار تمام مراحلی که برای رسم عمود منصف یک پاره‌‌خط توضیح دادیم، برای هر سه ضلع مثلث نیز انجام دهیم.

عمود منصف مستطیل

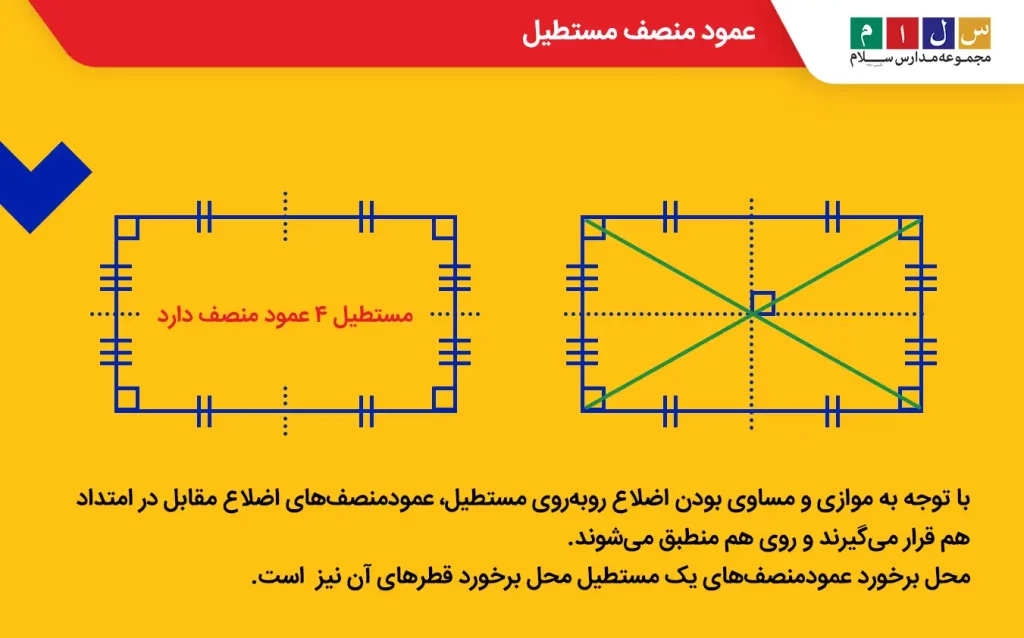
براساس تعریف عمود منصف، عمود منصف مستطیل خطی عمود بر اضلاع مستطیل است که ضلع‌‌ها را به دو قسمت مساوی تقسیم می‌‌کند. از آنجا که مستطیل از چهار ضلع ساخته شده است، این شکل هندسی دارای چهار عمود منصف خواهد بود. با توجه به موازی و مساوی بودن اضلاع روبه‌‌روی مستطیل، عمودمنصف‌‌های اضلاع مقابل در امتداد هم قرار می‌‌گیرند و روی هم منطبق می‌‌شوند.

عمودمنصف‌‌های یک مستطیل خط تقارن آن نیز محسوب می‌‌شوند و محل برخورد آن‌‌ها همان محل برخورد دو قطر مستطیل است. مربع نیز که نوعی مستطیل با چهار ضلع برابر است، چهار عمود منصف دارد. البته برخلاف مستطیل، در مربع قطر ها عمود منصف یکدیگرند و بر هم عمودند.

نحوه رسم عمود منصف در مستطیل، مربع و سایر اشکال هندسی مانند مراحل رسم عمود منصف در پاره‌‌خط و مثلث انجام می‌‌شود.

قضیه عمود منصف

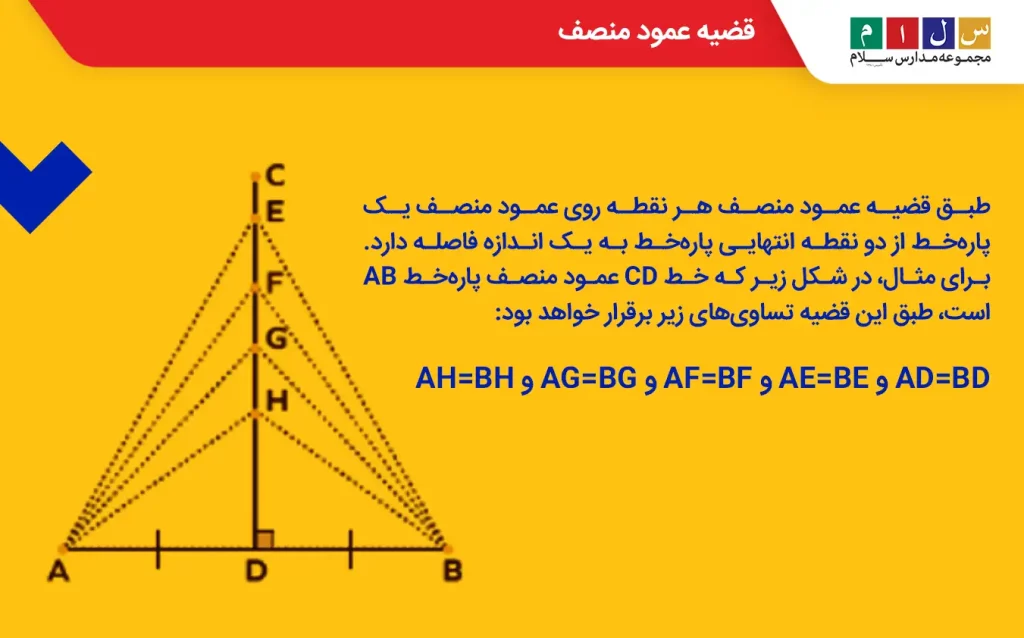
طبق قضیه عمود منصف هر نقطه روی عمود منصف یک پاره‌‌خط از دو نقطه انتهایی پاره‌‌خط به یک اندازه فاصله دارد. برای مثال، در شکل زیر که خط CD عمود منصف پاره‌‌خط AB است، طبق این قضیه تساوی‌‌های زیر برقرار خواهد بود: 

AH=BH و AG=BG و AF=BF و AE=BE و AD=BD

اثبات قضیه عمود منصف

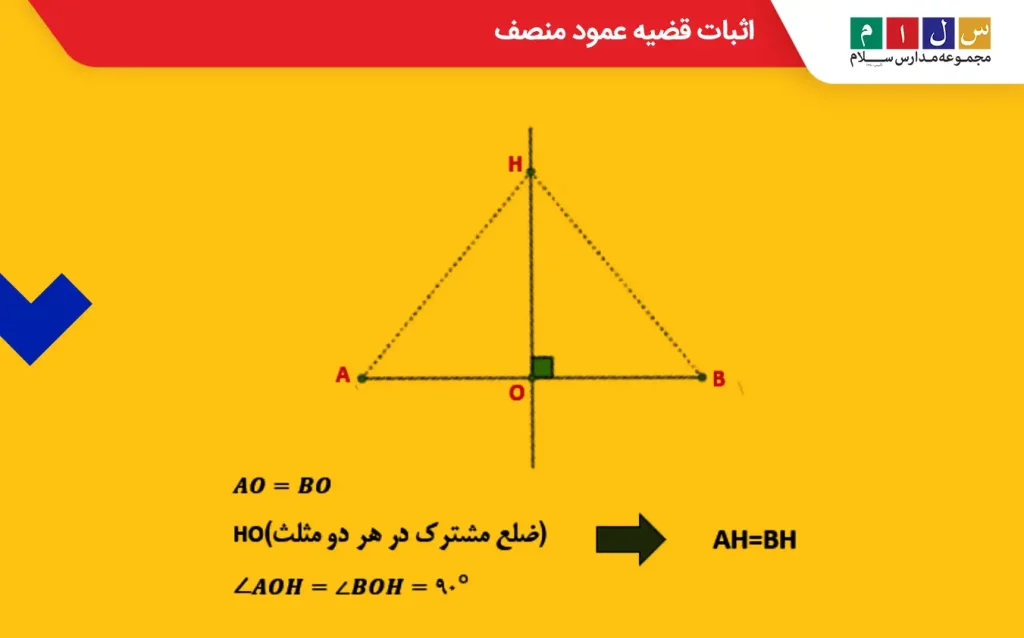
قضیه عمود منصف را می‌‌توان به کمک هم‌‌نهشتی مثلث‌‌ها اثبات کرد. یک نقطه دلخواه مانند H روی عمود منصف پاره‌‌خط AB در نظر بگیرید. عمود منصف پاره‌‌خط را در نقطه O قطع کرده است. با توجه به شکل زیر، دو مثلث AOH و BOH خواهیم داشت که تساوی‌‌های زیر در آن‌‌ها برقرار است:

• AO=BO
• HO (ضلع مشترک در هر دو مثلث)
• AOH=∠BOH=۹۰°

بنابراین، دو مثلث با داشتن دو ضلع و یک زاویه برابر (ض ز ض) هم‌‌نهشت محسوب می‌‌شوند. به‌‌این‌‌ترتیب، AH=BH است. این یعنی اینکه نقطه H از دو سر پاره‌‌خط AB فاصله یکسانی دارد.

عکس قضیه عمود منصف

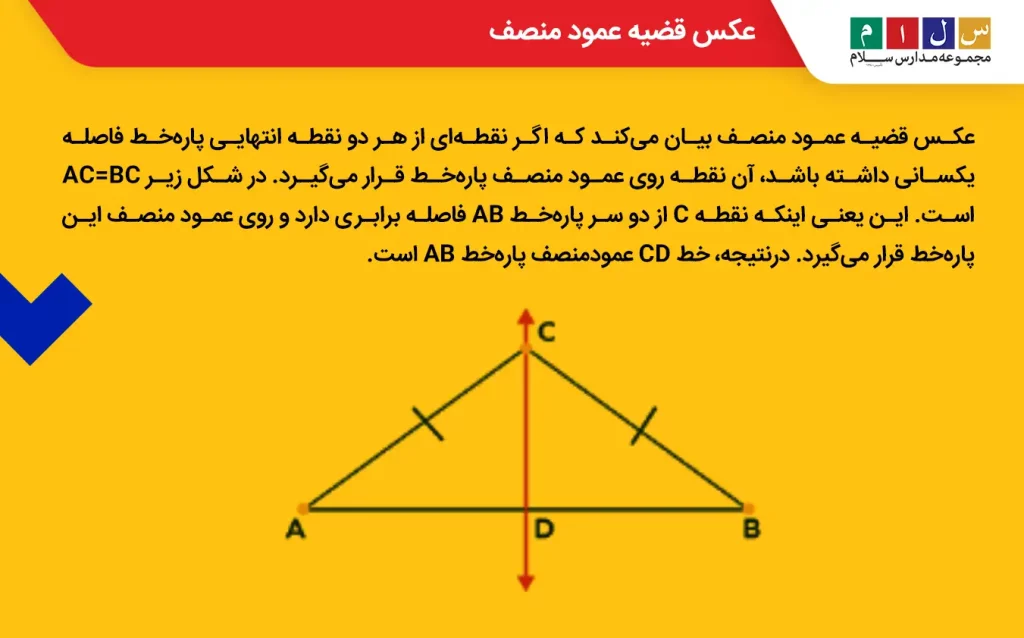
عکس قضیه عمود منصف بیان می‌‌کند که اگر نقطه‌‌ای از هر دو نقطه انتهایی پاره‌‌خط فاصله یکسانی داشته باشد، آن نقطه روی عمود منصف پاره‌‌خط قرار می‌‌گیرد. در شکل زیر AC=BC است. این یعنی اینکه نقطه C از دو سر پاره‌‌خط AB فاصله برابری دارد و روی عمود منصف این پاره‌‌خط قرار می‌‌گیرد. درنتیجه، خط CD عمودمنصف پاره‌‌خط AB است.

اثبات عکس قضیه عمود منصف

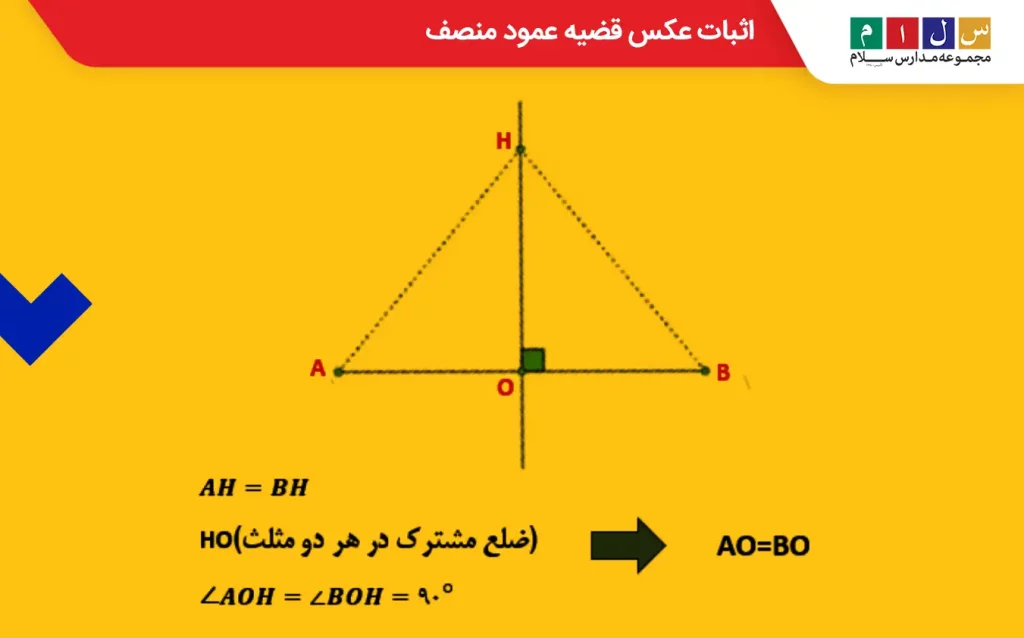
با توجه به عکس قضیه عمود منصف، در شکل زیر داریم AH=BH. پس باید ثابت کنیم که AO=BO است. در اینجا نیز از هم‌‌نهشتی مثلث‌‌ها کمک می‌‌گیریم. با مقایسه دو مثلث AOH و BOH به تساوی‌‌های زیر می‌‌رسیم:

• AH=BH
• HO (ضلع مشترک در هر دو مثلث)
• AOH=∠BOH=۹۰°

این تساوی‌‌ها نشان می‌‌دهند که دو مثلث هم‌‌نهشت‌‌اند. پس می‌‌توان نتیجه گرفت که AO=BO. به‌‌این‌‌ترتیب، نقطه H روی عمود منصف AB قرار دارد. 

مثال های حل شده عمود منصف

مثال ۱: اگر عمود منصف یک پاره‌‌خط به طول ۱۲ سانتی‌‌متر را رسم کنیم، اندازه هر قسمت از پاره‌‌خط چقدر خواهد بود؟

جواب: می‌‌دانیم که عمود منصف بر یک پاره‌‌خط عمود است و آن را به دو قسمت مساوی تقسیم می‌‌کند. ازآنجا که اندازه پاره‌‌خط ۱۲ سانتی‌‌متر است، طول هر کدام از دو قسمت مساوی برابر با مقدار زیر خواهد بود:

۱۲ ÷ ۲ = ۶سانتی متر

مثال ۲: در شکل زیر عمود منصف پاره‌‌خط BC از رأس A رسم شده است. با توجه به ویژگی‌‌های عمود منصف مقدار x را تعیین کنید.

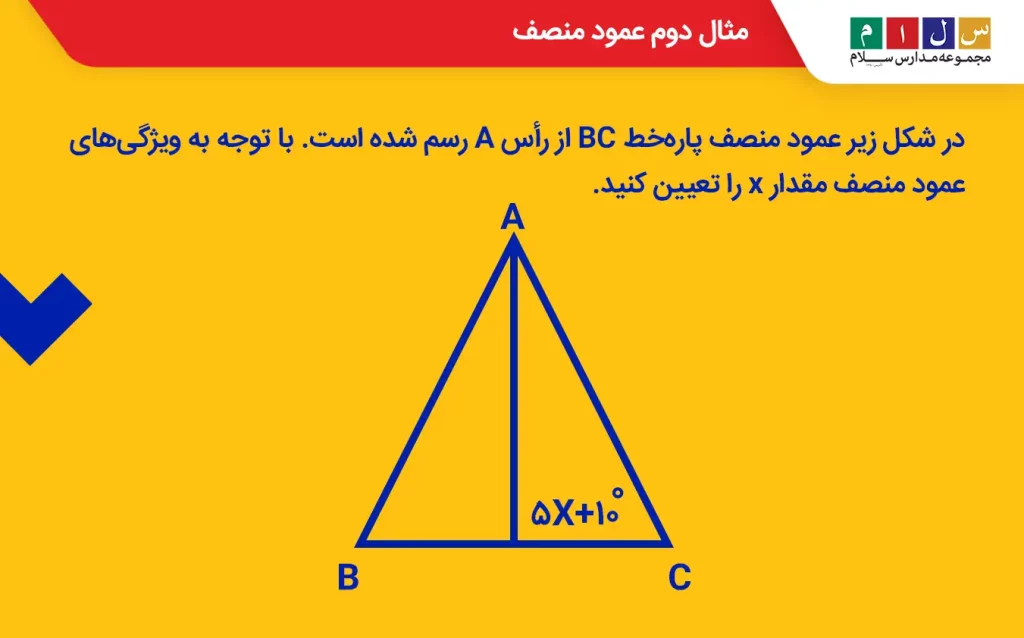
جواب: از آنجا که عمود منصف بر پاره‌‌خط BC عمود است، باید زاویه ۵x+۱۰ را برابر با ۹۰ درجه قرار دهیم.

۵ x + ۱۰ = ۹۰

۵x = ۹۰ – ۱۰ = ۸۰

۵x = ۸۰

۱۶ = x = ۸۰÷ ۵

مثال ۳: اگر AP عمود منصف BC باشد، مقدار x چقدر است؟

جواب: طبق قضیه عمود منصف، هر نقطه روی عمود منصف از دو سر پاره‌‌خطی که بر آن عمود شده است فاصله برابری دارد. پس داریم AB=AC. 

۲x + ۱۰ = ۱۸

۲x = ۱۸ – ۱۰ = ۸

۴= x = ۸ ÷ ۲

مثال ۴: در شکل زیر AP بر BC عمود است. مقدار x را بیابید.

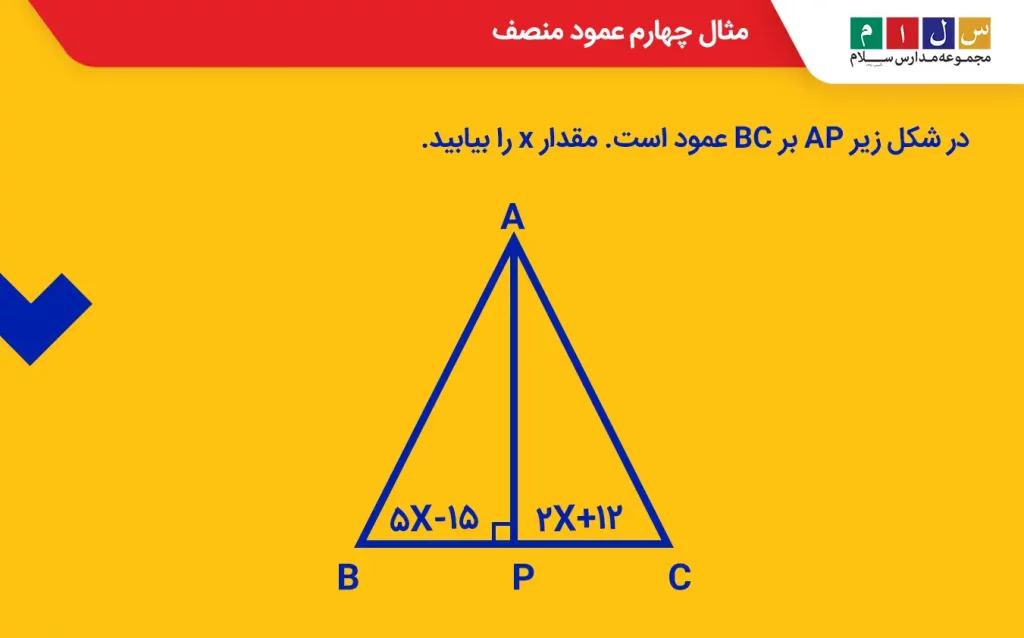
جواب: با توجه به قضیه عمود منصف PB=PC است. بنابراین، داریم:

۵x – ۱۵ = ۲ x + ۱۲

۵x – ۲x = ۱۲ + ۱۵

۳x = ۲۷

۹ = x = ۲۷ ÷ ۳

سخن پایانی

در این مقاله به معرفی یکی دیگر از مفاهیم هندسی به‌‌نام عمود منصف پرداختیم. عمود منصف به خط عمودی گفته می‌‌شود که یک پاره‌‌خط را نصف می‌‌کند و با آن زاویه قائمه تشکیل می‌‌دهد. برای هر پاره‌‌خطی تنها می‌‌توان یک عمود منصف رسم کرد که در آین آموزش مراحل رسم آن را با شکل توضیح دادیم.

علاوه‌‌بر این، قضیه عمود منصف و عکس آن را بیان کردیم و به اثبات آن پرداختیم. در آخر نیز با حل چند مثال با کاربرد مفهوم عمود منصف در مسائل هندسی آشنا شدیم. عمود منصف اگرچه مفهومی بسیار ساده و آسان به نظر می‌‌رسد اما همان‌‌طور که دیدیم، در حل بسیاری از مسائل کاربردی و کمک‌‌کننده است.

سؤالات متداول

1. عمود منصف یعنی چه؟
   عمود منصف خطی عمود است که یک پاره‌‌خط را نصف می‌‌کند و با آن زاویه ۹۰ درجه می‌‌سازد.
   
2. ویژگی عمود منصف چیست توضیح دهید.
   مطابق تعریف، ویژگی بارز عمود منصف این است که یک پاره‌‌خط را به دو قسمت مساوی تقسیم می‌‌کند و با آن زاویه قائمه می‌‌سازد. هر نقطه روی عمود منصف از دو سر پاره‌‌خطی که بر آن عمود شده است فاصله یکسانی دارد.
   
3. عمود منصف مثلث چیست؟
   منظور از عمود منصف مثلث خط عمود بر ضلع آن است که آن را به دو قسمت مساوی تقسیم می‌‌کند. با توجه به اینکه یک مثلث سه ضلع دارد تنها می‌‌توان سه عمود منصف برای آن رسم کرد.