قاعده چیست؟ ׀ تعریف قاعده در اشکال هندسی + شکل

هنگام توصیف اشکال هندسی و اجزایشان و همچنین محاسبه محیط و مساحت آن‌‌ها، واژه «قاعده» یا «پایه» بسیار به گوشمان خورده است. قاعده یک جسم یا یک شکل عموماً به یک ضلع یا وجهی که جسم یا شکل روی آن قرار دارد گفته شده و اغلب با ارتفاع عمود بر آن توصیف می‌‌شود. ازاین‌‌رو، برای درک بهتر بسیاری از اشکال هندسی، آشنایی با مفهوم قاعده حائز اهمیت خواهد بود. در ادامه این مقاله، خواهید آموخت که قاعده چیست و در اشکال گوناگون چگونه مشخص می‌‌شود.

قاعده چیست ؟

در هندسه معمولاً منظور از قاعده یا پایه یک شکل، ضلع یا وجهی است که شکل روی آن قرار می‌‌گیرد. قاعده یک شکل یا یک جسم را عموماً قسمت پایین آن در نظر می‌‌گیرند، بااین‌‌وجود، قاعده‌‌ها به اضلاع یا وجه‌‌های پایینی محدود نمی‌‌شوند و اکثر اوقات با ارتفاع نظیرشان یعنی پاره‌‌خط عمود بر آن‌‌ها می‌‌توان تعدادشان را مشخص کرد.

در اکثر اشکال هندسی دوبعدی و سه‌‌بعدی بسته به شکل ظاهری یک یا چند قاعده می‌‌تواند وجود داشته باشد. در ادامه بیشتر در‌‌این‌‌باره صحبت خواهیم کرد.

قاعده در اشکال هندسی دوبعدی

برای اشکال دوبعدی که از سه ضلع یا بیشتر ساخته شده‌‌اند، می‌‌توان یک یا چند قاعده در نظر گرفت. در این قسمت، تعداد قاعده‌‌ها در چندضلعی‌‌های معروف را با هم بررسی می‌‌کنیم.

قاعده مثلث

می‌‌دانیم که مثلث از سه ضلع و سه رأس ساخته شده است. همچنین از آموزش ارتفاع چیست به یاد داریم که اگر از رأس یک چندضلعی پاره‌‌خطی عمود بر ضلع مقابلش رسم کنیم، آن ضلع قاعده خواهد بود. بنابراین، در یک مثلث اضلاعی را که ارتفاع بر آن‌‌ها عمود است به‌‌عنوان قاعده در نظر می‌‌گیریم. توجه داشته باشید که گاهی اوقات برای رسم ارتفاع لازم است قاعده‌‌ها را امتداد دهیم.

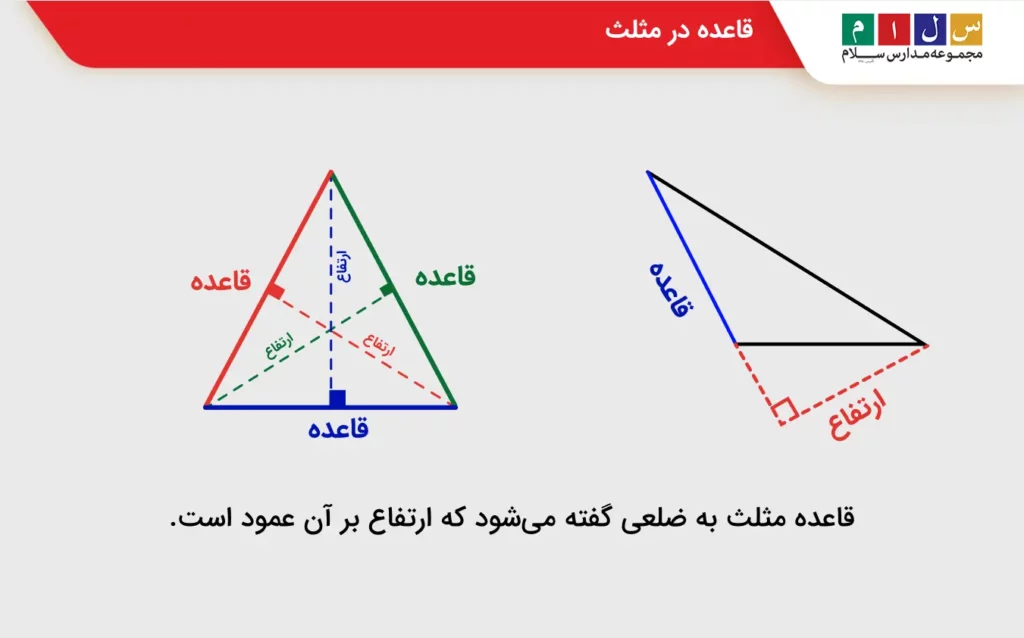
با داشتن قاعده و ارتفاع مثلث می‌‌توان مساحت آن را به‌‌راحتی محاسبه کرد. مساحت مثلث از فرمول زیر به‌‌دست می‌‌آید:

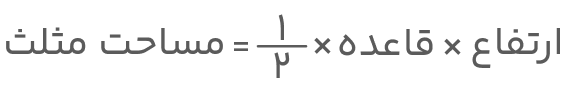
طبق این فرمول، اگر اندازه ارتفاع و مقدار مساحت یک مثلث مشخص باشد، می‌‌توانیم طول قاعده را به‌‌دست آوریم. برای درک بهتر، در ادامه به حل مثالی از محاسبه قاعده مثلث کلاس چهارم می‌‌پردازیم.

مثال: مساحت مثلثی ۲۷ سانتی‌‌متر مربع است. اگر ارتفاع آن ۶ سانتی‌‌متر باشد، قاعده آن چقدر خواهد بود؟
جواب: با جای‌‌گذاری مقادیر داده‌‌شده طول قاعده را می‌‌توانیم تعیین کنیم. خواهیم داشت:

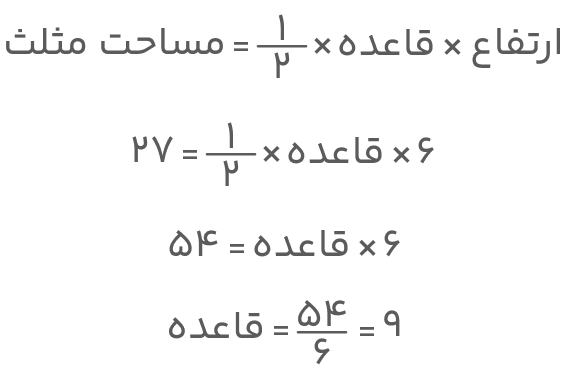
پس قاعده مثلث ۹ سانتی‌‌متر است.

قاعده مربع و مستطیل

مربع و مستطیل چهارضلعی‌‌هایی هستند که اضلاعشان دوبه‌‌دو با هم موازی و مساوی است. همچنین هر یک از آن‌‌ها دارای ۴ زاویه قائمه هستند که به‌‌خاطر عمود بودن اضلاعشان بر یکدیگر به‌‌وجود آمده‌‌اند. در این اشکال، ارتفاع و قاعده بر اضلاع منطبق‌‌اند. تصویر زیر این را به‌‌خوبی نشان می‌‌دهد.

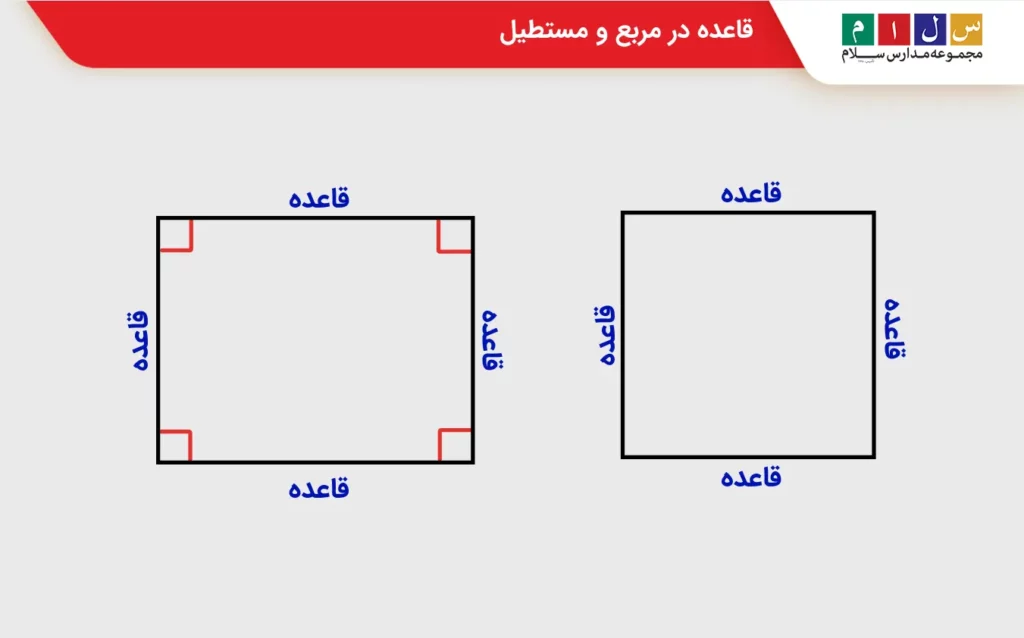
قاعده ذوزنقه

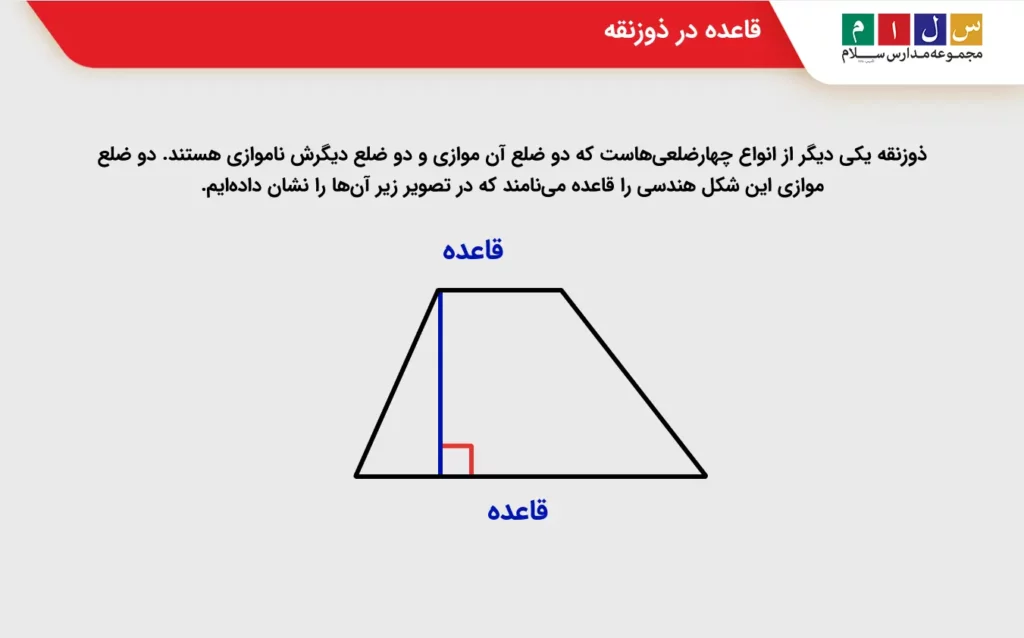
ذوزنقه یکی دیگر از انواع چهارضلعی‌‌هاست که دو ضلع آن موازی و دو ضلع دیگرش ناموازی هستند. دو ضلع موازی این شکل هندسی را قاعده می‌‌نامند که در تصویر زیر آن‌‌ها را نشان داده‌‌ایم. مشخص بودن طول قاعده‌‌ها هنگام محاسبه مساحت ذوزنقه به‌‌کارمان می‌‌آید. فرمول زیر نشان‌‌دهنده این موضوع است.

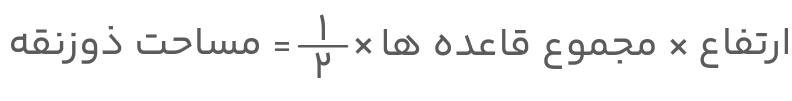
قاعده متوازی الاضلاع

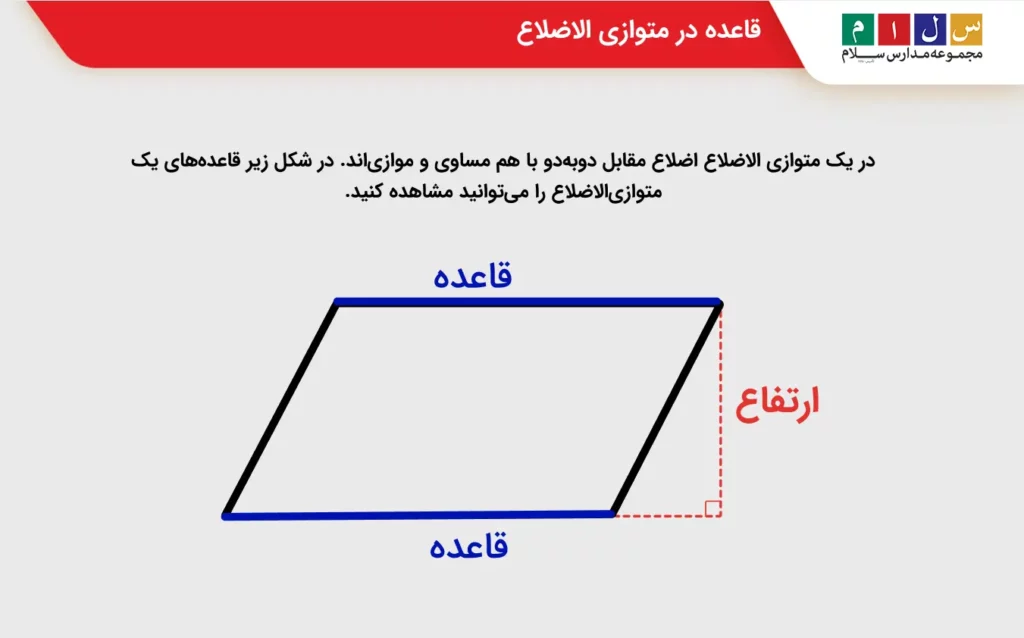
در یک متوازی الاضلاع اضلاع مقابل دوبه‌‌دو با هم مساوی و موازی‌‌اند. در شکل زیر قاعده‌‌های یک متوازی‌‌الاضلاع را می‌‌توانید مشاهده کنید. با مشخص بودن ارتفاع و قاعده می‌‌توانید مساحت متوازی الاضلاع را از رابطه زیر حساب کنید:

تا اینجای مقاله قاعده چیست کلاس پنجم ها و چهارم‌‌ها را با قاعده و کاربرد آن در محاسبه مساحت اشکال مسطح آشنا کردیم. در بخش‌‌های بعدی درمورد قاعده اشکال هندسی سه‌‌بعدی نیز توضیحات لازم را بیان خواهیم کرد.

قاعده در اشکال هندسی سه بعدی

ازآنجا که اشکال سه‌‌بعدی (فضایی) دارای حجم هستند، علاوه‌‌بر ضلع و رأس، وجه یا رویه نیز دارند. در این دسته از اشکال، قاعده یک وجه است. اشکالی که چند وجه دارند، می‌‌توانند بیشتر از یک وجه داشته باشند. در ادامه آموزش درباره قاعده‌‌های اشکال فضایی مختلف توضیح خواهیم داد.

قاعده مکعب

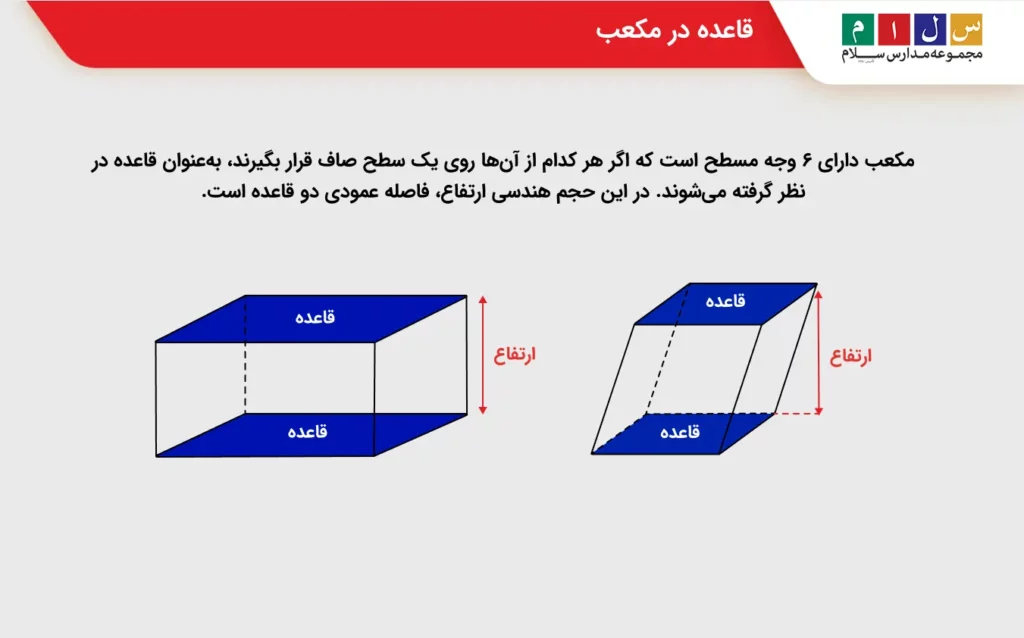
مکعب دارای ۶ وجه مسطح است که اگر هر کدام از آن‌‌ها روی یک سطح صاف قرار بگیرند، به‌‌عنوان قاعده در نظر گرفته می‌‌شوند. در این حجم هندسی ارتفاع، فاصله عمودی دو قاعده است. در شکل زیر قاعده مکعب قائم و مایل (متوازی‌‌السطوح) نشان داده شده است.

قاعده مخروط

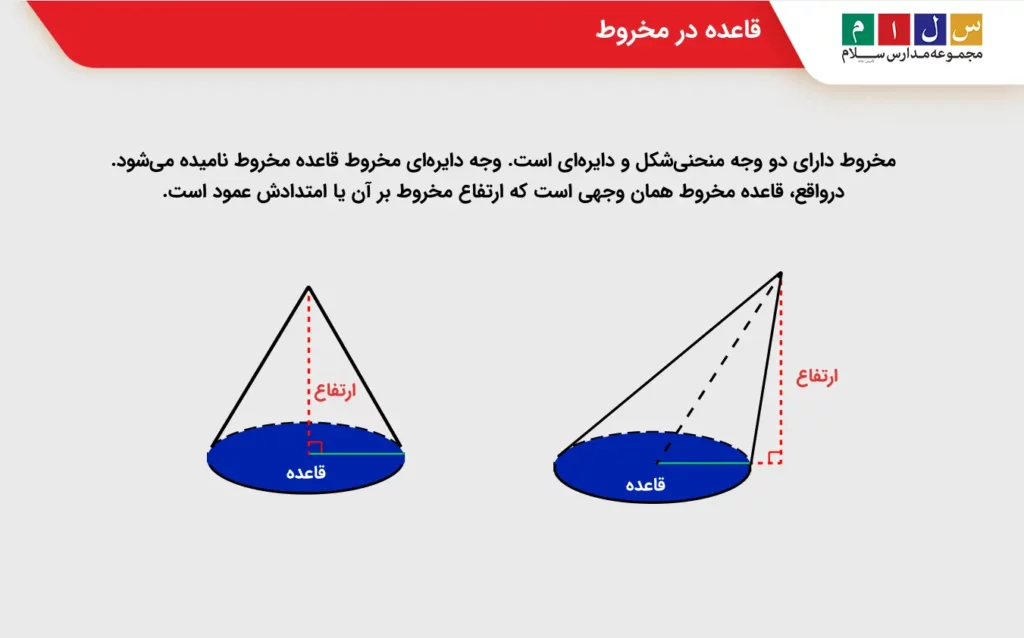
مخروط دارای دو وجه منحنی‌‌شکل و دایره‌‌ای است. وجه دایره‌‌ای مخروط قاعده مخروط نامیده می‌‌شود. درواقع، قاعده مخروط همان وجهی است که ارتفاع مخروط بر آن یا امتدادش عمود است. در شکل‌‌های زیر، قاعده مخروط قائم و مایل را مشاهده می‌‌کنید.

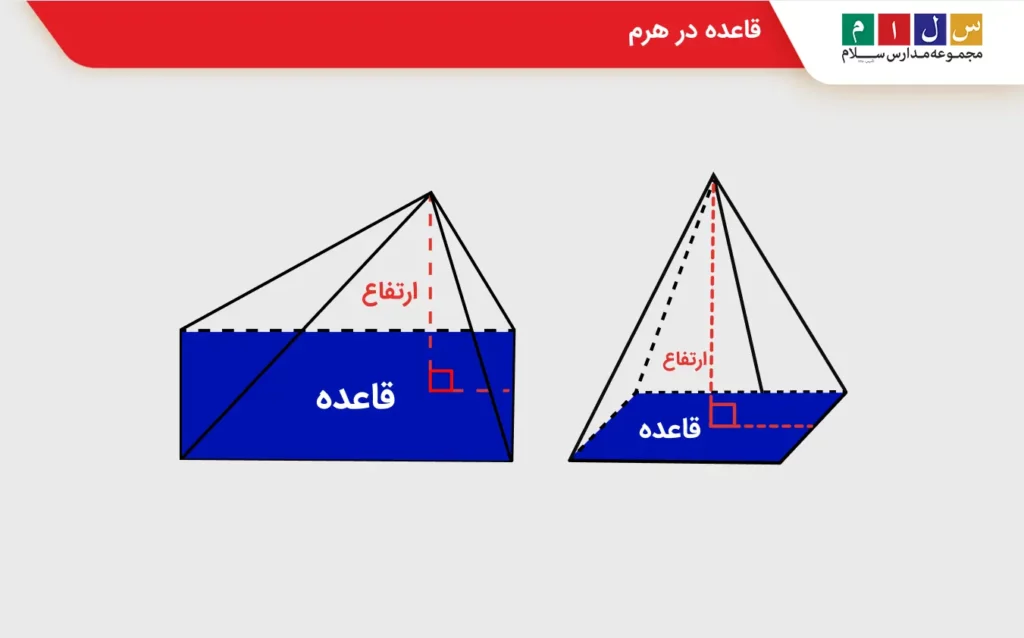
قاعده هرم

هرم و مخروط شبیه به یکدیگرند. اما تفاوت بارزی که با هم دارند، شکل قاعده آن‌‌ها است. در هرم قاعده به‌‌صورت یک چندضلعی است. اگر مایل هستید درمورد تفاوت‌‌های مخروط و هرم بیشتر بدانید، پیشنهاد ما مطالعه مقاله فرق هرم با مخروط است.

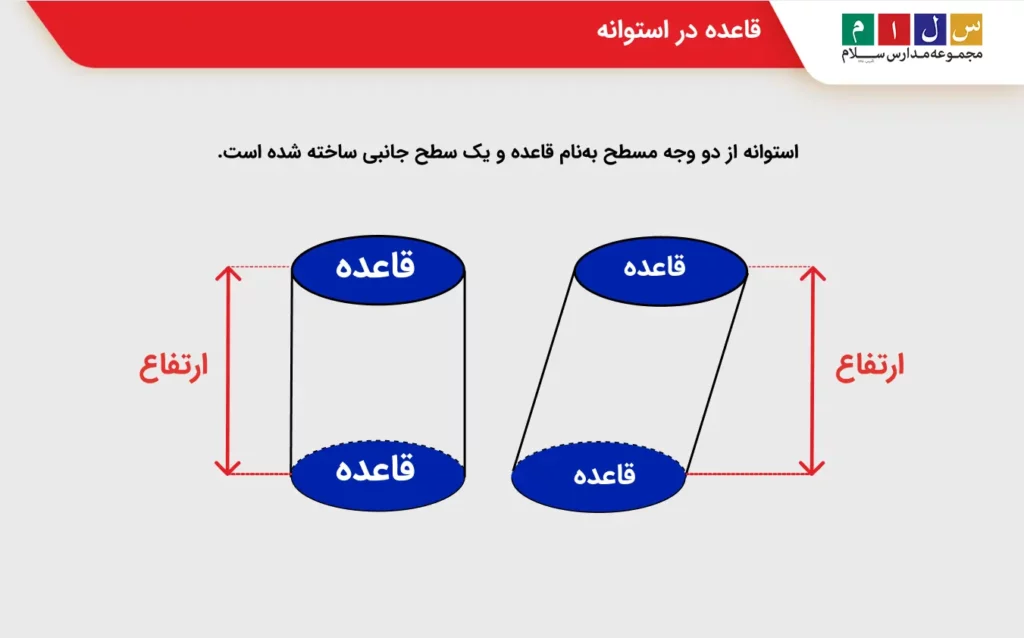
قاعده استوانه

استوانه از دو وجه مسطح به‌‌نام قاعده و یک سطح جانبی ساخته شده است. فاصله عمودی بین دو قاعده ارتفاع استوانه نام دارد که در تصویر زیر برای استوانه قائم و مایل آن را مشخص کرده‌‌ایم.

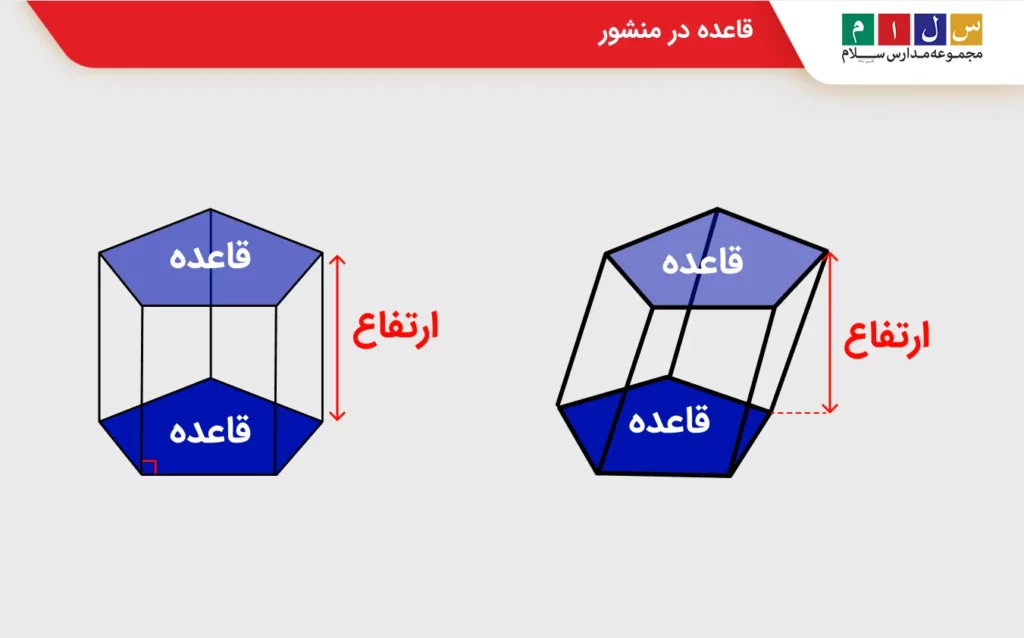
قاعده منشور

در یک منشور مانند استوانه دو قاعده روبه‌‌روی هم قرار دارند. قاعده‌‌های منشور به‌‌شکل چندضلعی هستند و موازی یکدیگرند.

فرمول محیط قاعده چیست ؟

محیط قاعده معمولاً در محاسبه مساحت جانبی اشکال فضایی به‌‌کار می‌‌رود و با توجه به شکل ظاهری آن فرمول محاسبه محیط می‌‌تواند متفاوت باشد. به‌‌عنوان مثال، اگر بخواهیم مساحت جانبی یک استوانه را تعیین کنیم، به محاسبه محیط قاعده دایره‌‌ای‌‌شکل آن نیاز داریم. برای اینکه این موضوع را بهتر متوجه شوید، یک مثال حل می‌‌کنیم.

مثال: محیط قاعده استوانه زیر را به‌‌دست آورید.

جواب: با توجه به اینکه قاعده به‌‌شکل دایره است، برای محاسبه محیط قاعده کافی‌‌ست از فرمول محیط دایره استفاده کنیم. در این صورت محیط قاعده از رابطه زیر به‌‌دست خواهد آمد:

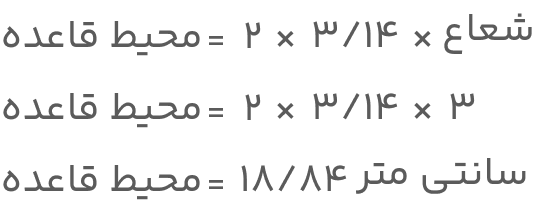
پیشنهاد مطالعه: محیط دایره چیست؟

فرمول مساحت قاعده چیست ؟

تعیین مساحت قاعده هر حجم هندسی بستگی به شکل آن دارد که ما در مقاله مساحت چیست به صورت کامل توضیح داده ایم. برای مثال، در یک منشور فرمول مساحت قاعده متفاوت از استوانه است. حتی در منشورهای گوناگون نیز این تفاوت وجود دارد. مثلاً اگر قاعده منشور مثلثی‌‌شکل باشد، فرمول آن از فرمول مساحت مثلث به‌‌دست می‌‌آید، اما اگر یک شش ضلعی باشد، فرمول آن متفاوت خواهد بود.

مثال: مساحت قاعده منشور زیر را حساب کنید.

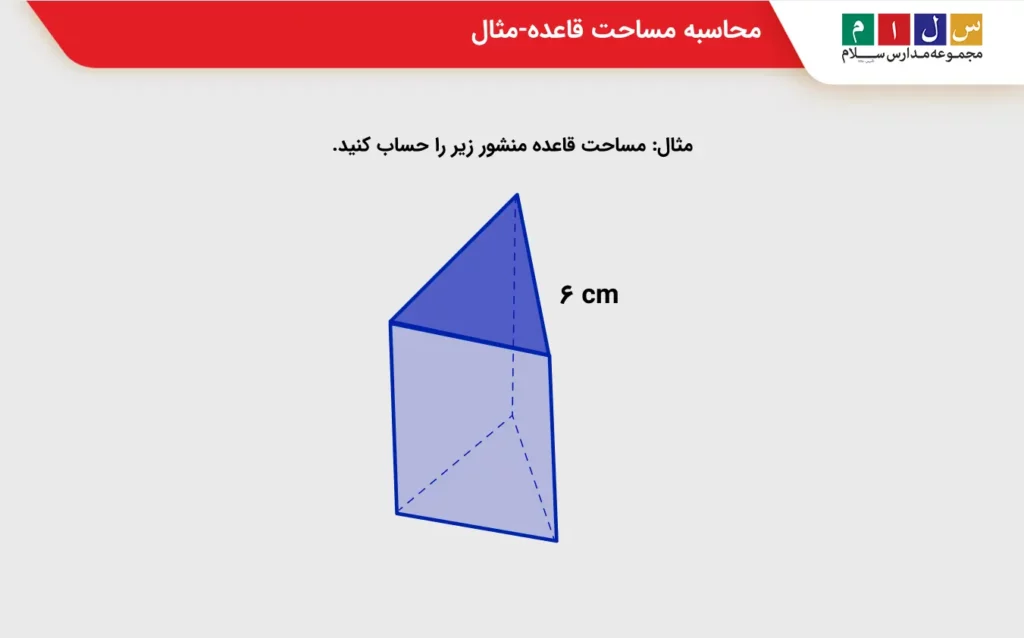
جواب: قاعده منشور داده‌‌شده به‌‌شکل مثلث متساوی الاضلاع است. برای اینکه مشخص کنیم مساحت قاعده چیست از فرمول مساحت مثلث متساوی الاضلاع استفاده می‌‌کنیم. داریم:

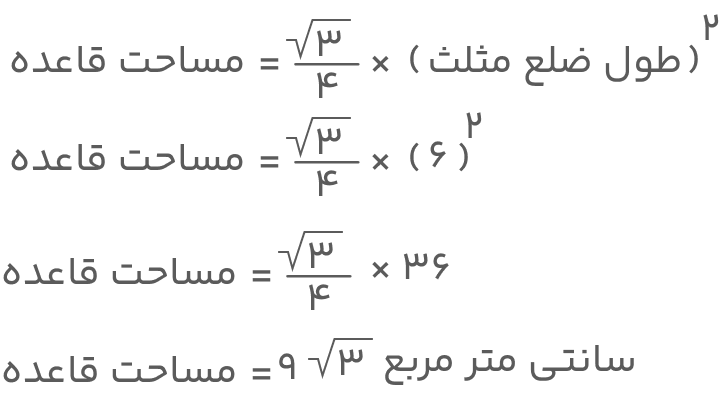
سخن پایانی

در این آموزش یاد گرفتیم که قاعده چیست در ریاضی تعریف قاعده بیشتر به اشکال هندسی اطلاق می‌‌شود. برای همین، در پاسخ به سؤال قاعده چیست به زبان ساده باید بگوییم که منظور از قاعده ضلع یا وجه یک شکل هندسی است که اغلب در کف آن واقع شده و می‌‌توان آن را به‌‌عنوان یک تکیه‌‌گاه برای شکل هندسی در نظر گرفت.

در این مقاله سعی کردیم برای درک بهتر مفهوم قاعده، قاعده‌‌های اشکال هندسی معروف را بررسی کنیم. شما نیز می‌‌توانید به‌‌عنوان تمرین به اشیاء پیرامون خود نگاه کرده و قاعده آن‌‌ها را مشخص کنید.

سؤالات متداول

1. قاعده در ریاضی چیست ؟
   قاعده در ریاضی اغلب به ضلع یا وجه پایینی شکل‌‌های هندسی مربوط می‌‌شود.
2. فرمول محیط قاعده چیست ؟
   محیط قاعده فرمول مشخصی ندارد. اما به‌‌طور کلی، در شکل‌‌های هندسی سه‌‌بعدی محیط قاعده از اندازه دور آن به‌‌دست می‌‌آید.
3. فرمول مساحت قاعده چیست ؟
   فرمول مساحت قاعده در حجم‌‌های هندسی گوناگون، براساس شکل قاعده می‌‌تواند متفاوت باشد.