میانگین چیست؟ ׀ تعریف و روش محاسبه + حل مثال

در بسیاری از مسائل روزمره، گاهی اوقات با تعداد زیادی داده یا عدد مواجه می‌شویم که بررسی و بیان تک‌تک آن‌ها علاوه‌بر وقت‌گیر بودن برایمان دشوار هم خواهد بود. در اینگونه مواقع، با استفاده از یک مفهوم ریاضی به‌نام میانگین می‌توان این مشکل را برطرف کرد. درواقع، میانگین نماینده مجموعه بزرگی از اعداد است. اگر می‌خواهید بدانید میانگین چیست و چه کاربردی دارد، با ادامه این مطلب همراه باشید. در این مطلب، علاوه‌بر تعریف میانگین، روش محاسبه آن را با حل چند نمونه سؤال آموزش خواهیم داد.

میانگین چیست؟

واژه میانگین به معنای متوسط یا حد وسط یک چیز است. میانگین یک مفهوم ریاضی است که با استفاده از آن می‌توان مجموعه بزرگی از اعداد را با یک عدد نمایش داد. برای مثال، زمانی که نیاز داریم عملکرد کل دانش‌آموزان یک کلاس را در یک درس خاص بسنجیم، به‌جای بررسی عملکرد تک‌تک دانش‌آموزان که کاری وقت‌گیر است و ممکن است اطلاعات درستی هم به ما ندهد، از میانگین نمرات آن‌ها استفاده می‌کنیم. 

خوب است بدانید که گاهی اوقات به میانگین، متوسط یا معدل هم گفته می‌شود.

کاربرد میانگین

در بخش قبل، نمونه‌ای از کاربرد میانگین یعنی میانگین گرفتن از نمرات دانش‌آموزان در یک درس را بیان کردیم. این مثال، نمونه رایج و بارز کاربرد میانگین در زندگی روزمره است که همه ما در دوران تحصیل با آن سروکار داریم. البته، نمونه‌های بسیار دیگری از کاربرد این مفهوم ریاضی را هم می‌توان نام برد. مثلاً زمانی که می‌خواهند دمای یک شهر را در طول یک فصل نشان دهند، از مقدار دمای آن شهر در طول سه ماه میانگین گرفته می‌شود. این کار، تصمیم‌گیری درمورد دمای آن شهر را بسیار راحت‌تر می‌کند تا اینکه دمای ۹۰ روز آن شهر را تک‌به‌تک بررسی کنند. 

میانگین قد دانش‌آموزان یک کلاس، میانگین درآمد سالانه یک شخص، میانگین مطالعه یا ورزش روزانه یا هفتگی، همگی نمونه‌هایی از کاربرد میانگین هستند. احتمالاً با خود می‌گویید استفاده از میانگین چه کمکی می‌تواند به ما بکند. بگذارید یا یک مثال این موضوع را توضیح دهیم. فرض کنید می‌خواهید بدانید در هفته یا در ماه چه مقدار پول پس‌انداز کرده‌اید و درمقایسه با ماه قبل پس‌اندازتان بیشتر شده است یا کمتر.

واضح است که بررسی تمام پس‌اندازهای روزانه شما نمی‌تواند اطلاعات درستی درمورد افزایش یا کاهش میزان پس‌اندازتان به شما بدهد. در اینجا میانگین گرفتن می‌تواند به شما کمک کند. درواقع، شما با میانگین گرفتن از مقدار پس‌انداز هفتگی یا ماهانه خود، مجموعه‌ای از اعداد پراکنده را به یک عدد واحد تبدیل می‌کنید و می‌توانید با استفاده از آن، از میزان افزایش یا کاهش مقدار پس‌اندازتان آگاهی پیدا کنید و برنامه‌ریزی بهتری برای بهبود آن داشته باشید.

اگر به‌عنوان یک دانش‌آموز قصد دارید برنامه‌ریزی مالی مناسبی برای هزینه‌های خود داشته باشید، پیشنهاد می‌کنیم سری به مقاله جدول بودجه بزنید. در آنجا روش‌های کاربردی و مفیدی برای مدیریت مالی ارائه کرده‌ایم.

پیشنهاد مطالعه: نسبت های مساوی را چگونه به دست آوریم؟

فرمول میانگین

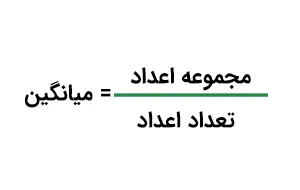
در ریاضیات، انواع مختلفی از میانگین وجود دارد. ما در اینجا فقط به نوع رایج آن یعنی میانگین حسابی می‌پردازیم. فرمول میانگین برای یک مجموعه داده یا مشاهدات معین برابر است با مجموع داده‌ها یا مشاهدات تقسیم بر تعداد آن‌ها. به‌طور کلی، می‌توان گفت میانگین چند عدد برابر با مجموع کل اعداد تقسیم بر تعداد اعداد است و فرمول آن به‌صورت زیر نوشته می‌شود:

تعداد اعداد یا مشاهدات ÷ مجموع اعداد یا مشاهدات = میانگین

برای درک بهتر مفهوم میانگین به تصویر زیر نگاه کنید. سمت چپ تصویر، سه دسته سیب به تعداد ۶، ۱۱ و ۷ تا را نشان می‌دهد. اگر بخواهیم میانگین این سه دسته سیب را به‌دست آوریم، باید ابتدا تعداد سیب‌های هر دسته را به‌صورت زیر با هم جمع کنیم تا تعداد کل سیب‌ها به‌دست آید:

۲۴ = ۷ + ۱۱+ ۶ = مجموع سیب‌ها

سپس مقدار حاصل را بر تعداد دسته‌های سیب یعنی ۳ تقسیم می‌کنیم:

۸ = ۳ ÷ ۲۴

پس میانگین تعداد سیب‌ها در هر ستون برابر با ۸ است. همان‌طور که در تصویر زیر هم می‌بینید، مجموع سیب‌ها در دسته‌های ۸ تایی برابر با مجموع سیب‌ها در دسته‌های ۶، ۱۱ و ۷ تایی است. درواقع، ما با میانگین گرفتن از سه دسته سیب، تعداد کل سیب‌ها را در سه دسته برابر تقسیم کرده‌ایم.

محاسبات مربوط به میانگین را می‌توان به‌طور خلاصه‌تر و به‌صورت کسری هم نوشت:

در این صورت، میانگین تعداد سیب‌ها به‌صورت زیر محاسبه خواهد شد:

میانگین سیب ها =

$$\frac{۶+۱۱+۷}{۳}=\frac{۲۴}{۳}=۸$$

پیشنهاد مطالعه: تقارن به زبان ساده همراه با شکل

میانگین اعداد صحیح

در مقاله اعداد صحیح چه اعدادی هستند گفتیم که اعداد صحیح شامل اعداد مثبت، منفی و صفر هستند که بخش اعشاری و کسری ندارند. همچنین، در آنجا روش جمع و تفریق این اعداد را با مثال توضیح دادیم. در ادامه برای آموزش میانگین اعداد صحیح یک مثال با هم حل می‌کنیم تا با روش و فرمول میانگین اعداد صحیح آشنا شوید.

فرض کنید می‌خواهیم میانگین اعداد ۴، ۷-، ۱۶، ۵- و ۳- را به‌دست آوریم. برای محاسبه میانگین اعداد داده‌شده، ابتدا آن‌ها را با هم جمع می‌کنیم. توجه داشته باشید زمانی که چند عدد صحیح را با هم جمع می‌کنید، برای اینکه کمتر دچار اشتباه شوید، اعداد مثبت را با هم و اعداد منفی را با هم به‌طور جداگانه جمع کنید، سپس، علامت مثبت یا منفی را کنار آن‌ها قرار دهید و جواب نهایی جمع موردنظر را به‌دست آورید. حاصل‌جمع اعداد داده‌شده برابر است با

۵ = ۲۰-۱۵ = (۱۵-) +۲۰ = (۳-) + (۵-) + ۱۶ + (۷-) + ۴

تعداد اعداد ۵ است. پس در این مرحله باید پاسخ به‌دست‌آمده را بر تعداد اعداد یعنی ۵ تقسیم کنیم.

۱ = ۵ ÷ ۵ = میانگین

مقدار میانگین اعداد برابر با یک است. 

می‌توانیم میانگین اعداد موردنظر را به‌طور خلاصه به‌صورت زیر محاسبه کنیم:

میانگین =

$$\frac{۴+(-<!--\; -\; -->۷)+۱۶+(-<!--\; -\; -->۵)+(-<!--\; -\; -->۳)}{۵}=\frac{۲۰+(-<!--\; -\; -->۱۵)}{۵}=\frac{۲۰-<!--\; -\; -->۱۵}{۵}=\frac{۵}{۵}=۱$$

پیشنهاد مطالعه: اعداد اعشاری و عملیات ریاضی در آن ها

روش سریع محاسبه میانگین

گاهی اوقات ممکن است اعداد داده‌شده برای میانگین گرفتن تک‌رقمی نباشند و با اعداد بزرگ‌تری مواجه شویم. جمع بستن و درنتیجه میانگین‌گیری چنین اعدادی می‌تواند دشوار و وقت‌گیر باشد. برای حل این مشکل، می‌توان روش سریع‌تر و راحت‌تری در پیش گرفت. با یک مثال، این روش را توضیح می‌دهیم.

اعداد ۱۳، ۱۱، ۱۴، ۱۶، ۱۷، ۱۶، ۱۵، ۱۴ را در نظر بگیرید. اگر بخواهیم میانگین این اعداد را سریع محاسبه کنیم به‌صورت زیر عمل می‌کنیم:

گام اول: ابتدا خودمان حدس می‌زنیم که میانگین این اعداد چیست. توجه داشته باشید که اعداد حدسی شما برای میانگین معقول باشد و از اعدادی که داده شده است، خیلی بزرگ‌تر یا کوچک‌تر نباشد. مثلاً در اینجا نمی‌توانیم عدد ۹ یا ۲۰ را به‌عنوان میانگین حدسی در نظر بگیریم زیرا در محدوده اعداد موردنظر قرار ندارند و غیرمعقول به نظر می‌رسند. فرض می‌کنیم میانگین اعداد ۱۶ باشد.
گام دوم: میانگین حدسی خود یعنی ۱۶ را از تمام اعداد داده‌شده کم می‌کنیم.

  ۱- = ۱۵-۱۶     ۰ = ۱۶-۱۶      ۳- = ۱۳-۱۶
۲- = ۱۴-۱۶      ۱ = ۱۷-۱۶        ۵- = ۱۱-۱۶
      ۰ = ۱۶-۱۶      ۲- = ۱۴-۱۶

گام سوم: حاصل تفریق‌های بالا را با هم جمع می‌زنیم و بر تعداد اعداد یعنی ۸ تقسیم می‌کنیم.

– ۳- ۵ – ۲ + ۰ + ۱ + ۰ -۱-۲ = -۱۲

$$\frac{-<!--\; -\; -->۱۲}{۸}=-<!--\; -\; -->۱/۵$$

اگر پاسخ به‌دست‌آمده مانند همین مثالی که زدیم منفی باشد، یعنی عددی که حدس زده‌ایم، مقدارش بیشتر از مقدار میانگین واقعی بوده است، اما اگر جواب مثبت باشد، یعنی میانگین حدسی مقدارش کمتر از مقدار میانگین واقعی است. در مثالی که حل کرده‌ایم عدد ۱/۵- به‌دست آمده است. این پاسخ نشان می‌دهد که میانگین حدسی ما یعنی ۱۶ از میانگین واقعی ۱/۵ واحد بیشتر است. پس باید ۱/۵ را از ۱۶ کم کنیم تا مقدار میانگین واقعی یعنی ۱۴/۵ به‌دست آید. در ادامه یک مثال دیگر حل می‌کنیم تا این روش بیشتر برایتان جا بیفتد.

مثال: میانگین اعداد ۲۰، ۲۲، ۲۵، ۲۳، ۲۰، ۲۵ را تعیین کنید.
جواب: با توجه به توضیحاتی که دادیم، ابتدا مقدار میانگین این اعداد را خودمان حدس می‌زنیم. فرض کنید عدد حدسی ما ۲۲ است. عدد ۲۲ را از اعداد داده‌شده کم می‌کنیم.

  ۳ = ۲۵-۲۲       ۰ = ۲۲-۲۲    ۲- = ۲۰-۲۲
۳ = ۲۵-۲۲     ۲- = ۲۰-۲۲      ۱ = ۲۳-۲۲

حاصل تفریق‌ها را با هم جمع کرده و بر تعداد اعداد یعنی ۶ تقسیم می‌کنیم.

-۲+۰+۳+۱-۲+۳=۳

$$\frac{۳}{۶}=۰/۵$$

همان‌طور که می‌بینید، مقدار حاصل برابر با ۰/۵ است. عدد به‌دست‌آمده یک عدد مثبت است. پس باید طبق توضیحاتی که دادیم مقدار ۰/۵ را به میانگین حدسی یعنی ۲۲ اضافه کنیم تا مقدار میانگین واقعی مشخص شود. بنابراین، مقدار میانگین واقعی برابر با ۲۲/۵ خواهد بود.

پیشنهاد مطالعه: زاویه چیست و انواع زاویه چه هستند؟

نمونه سؤال میانگین با جواب

در این قسمت، برای درک بهتر مبحث میانگین به حل چند نمونه سؤال می‌پردازیم.

سؤال ۱: میانگین اعداد

$$\frac{۵}{۶}و\frac{۲}{۳}$$

را به‌صورت کسری به‌دست آورید.

$$\frac{۳}{۶}=۰/۵$$

جواب: ابتدا دو عدد کسری را با هم جمع می‌زنیم. سپس، مقدار حاصل را بر تعداد داده‌ها یعنی ۲ تقسیم می‌کنیم.

$$\frac{۲}{۳}+\frac{۵}{۶}=\frac{۲\times <!--\; \times \; -->۲}{۳\times <!--\; \times \; -->۲}+\frac{۵}{۶}=\frac{۴}{۶}+\frac{۵}{۶}=\frac{۹}{۶}$$

میانگین =

$$\frac{۹}{۶}÷<!--\; ÷\; -->۲=\frac{۹}{۶}\times <!--\; \times \; -->\frac{۱}{۲}=\frac{۹}{۱۲}=\frac{۹÷<!--\; ÷\; -->۳}{۱۲÷<!--\; ÷\; -->۳}=\frac{۳}{۴}$$

سؤال ۲: اعداد زیر، دمای یک شهر را در طول یک هفته نشان می‌دهند. میانگین دمای این شهر در این هفته چند درجه بوده است؟

۱-، ۰/۵-، ۱/۵، ۲، ۱، ۱/۵، ۰/۵

جواب: مقدار دماها را با هم جمع کرده و بر تعداد آن‌ها یعنی ۷ تقسیم می‌کنیم.

میانگین دما =

$$\frac{-<!--\; -\; -->۱-<!--\; -\; -->۰/۵+۱/۵+۲+۱+۱/۵+۰/۵}{۷}=\frac{۵}{۷}\approx <!--\; \approx \; -->۰/۷$$

میانگین دما تقریباْ ۰/۷ درجه است.

سؤال ۳: نمرات دانش‌آموزان یک کلاس در درس ریاضی به‌صورت زیر است. میانگین نمرات این دانش‌آموزان چقدر است؟ 

تعداد دانش‌آموز	۳	۳	۵	۲	۵	۲
نمره	۲۰	۱۷	۱۹	۱۸/۵	۱۶	۱۵/۵

جواب: فرمول محاسبه میانگین نمرات این کلاس به‌صورت زیر نوشته می‌شود:

تعداد دانش‌آموزان ÷ مجموع نمرات = میانگین نمرات

ابتدا مجموع نمرات را محاسبه می‌کنیم. خواهیم داشت:

میانگین نمرات

$$=(۳\times <!--\; \times \; -->۲۰)+(۳\times <!--\; \times \; -->۱۷)+(۵\times <!--\; \times \; -->۱۹)+(۲\times <!--\; \times \; -->۱۸/۵)+(۵\times <!--\; \times \; -->۱۶)+(۲\times <!--\; \times \; -->۱۵/۵)$$

میانگین نمرات =

$$۶۰+۵۱+۹۵+۳۷+۸۰+۳۱=۳۵۴$$

طبق جدول، تعداد دانش‌آموزان یا به‌عبارتی تعداد نمره‌ها ۲۰ است. بنابراین، مقدار میانگین نمرات دانش‌آموزان به‌صورت زیر محاسبه خواهد شد:

۱۷/۷ =۲۰ ÷ ۳۵۴=میانگین نمرات

پس میانگین نمرات دانش‌آموزان در درس ریاضی ۱۷/۷ است.
سؤال ۴: نرگس به‌همراه دوستش آیدا با هم قرار گذاشته‌اند که ساعاتی از هفته را به مطالعه کتاب‌های غیردرسی اختصاص دهند و تعداد صفحاتی را که در طول هفته مطالعه می‌کنند، یادداشت کنند. تعداد صفحاتی که هر دوی آن‌ها طی یک ماه مطالعه کرده‌اند، در جدول زیر نشان داده شده است. میانگین مطالعه هفتگی نرگس و آیدا در طول یک ماه چند صفحه است؟

هفته‌ها	تعداد صفحات نرگس	تعداد صفحات آیدا
هفته اول	۱۲۳	۱۱۸
هفته دوم	۱۳۷	۱۲۹
هفته سوم	۱۱۹	۱۲۴
هفته چهارم	۱۲۸	۱۳۰

جواب: برای یافتن میانگین تعداد صفحات مطالعه‌شده توسط آیدا و نرگس، ابتدا باید تعداد کل صفحاتی را که هر یک از آن‌ها در طول یک ماه مطالعه کرده‌اند، به‌دست آوریم. بنابراین، خواهیم داشت:

تعداد صفحات نرگس =
۱۲۳+۱۳۷+۱۱۹+۱۲۸=۵۰۷

تعداد صفحات آیدا =
۱۸۸+۱۲۹+۱۲۴+۱۳۰

در گام بعدی، مجموع صفحات آیدا و نرگس را بر تعداد داده‌ها (هفته‌ها) یعنی ۴ تقسیم می‌کنیم تا میانگین مطالعه هفتگی هر کدام در طول یک ماه به‌دست آید.

میانگین مطالعه نرگس=

$$\frac{۵۰۷}{۴}=۱۲۶/۷۵$$

میانگین مطالعه آیدا =

$$\frac{۵۰۱}{۴}=۱۲۵/۲۵$$

با توجه به جواب‌های به‌دست‌آمده می‌توان گفت که میانگین مطالعه هفتگی نرگس اتدکی بیشتر از آیدا است.

پیشنهاد مطالعه: نیمساز چیست و چگونه رسم می‌شود؟

سخن پایانی

در این مقاله به تعریف میانگین در ریاضی پرداختیم و گفتیم که میانگین یک عدد واحد برای نمایش مجموعه‌ای از اعداد و داده‌هاست. میانگین گرفتن از اعداد علاوه‌بر اینکه به درک بهتر ما از داده‌ها کمک می‌کند، اطلاعات مفیدی نیز در اختیار ما قرار خواهد داد. میانگین چند داده از تقسیم مجموع داده‌ها بر تعداد داده‌ها به‌دست می‌آید. البته، روش سریع‌تری هم برای محاسبه میانگین وجود دارد که معمولاً برای اعداد بزرگ کاربردی‌تر است و در این آموزش مفصل درمورد آن صحبت کردیم. البته، توجه داشته باشید که حل کردن تمرین‌های بیشتر در این زمینه می‌تواند تسلط شما را در میانگین گرفتن بیشتر کند.  

سؤالات متداول

1. میانگین در ریاضی یعنی چه؟
   میانگین در ریاضی به معنای متوسط یا حد وسط چیزی است که گاهی اوقات به آن معدل هم می‌گویند.
2. میانگین چند داده را چه می‌گویند؟
   میانگین چند داده را متوسط آن داده‌ها می‌گویند.
3. فرمول محاسبه میانگین چیست؟
   فرمول میانگین برابر است با مجموع داده‌ها تقسیم بر تعداد داده‌ها.