تقارن در دنیای پیرامون ما از بدن انسان گرفته تا طبیعت و معماری زیبایی خاصی به اطرافمان بخشیده است. شاید رایج‌ترین مثال‌ها برای تقارن در طبیعت، بال‌های پروانه، کندوهای عسل و دانه‌های برف باشد که اجزای آن‌ها در دو طرف شبیه و قرینه یکدیگر هستند. البته، نمونه‌های دیگری از تقارن در زندگی روزمره ما یافت میشود که با نوع تقارنِ مثال‌هایی که زدیم متفاوت‌اند. درواقع، تقارن انواع و اقسام مختلفی دارد که درادامه آن‌ها را همراه با مثال تصویری به شما معرفی می‌کنیم.
تقارن چیست؟
در ریاضیات و به‌ویژه در هندسه، اگر بتوان یک شکل را به دو نیمه یکسان و مشابه تقسیم کرد، طوری که یک نیمه قرینه و بازتاب نیمه دیگر باشد، آن شکل دارای تقارن یا به‌عبارتی متقارن است. به‌عنوان مثال، به تصویر گلی که در شکل زیر نشان داده شده است، نگاه کنید. اگر یک خط فرضی در وسط آن بکشیم، می‌توانیم آن را به دو قسمت مساوی تقسیم کنیم. یعنی گل موردنظر در تصویر زیر متقارن است.
اما اگر یک شکل متقارن نباشد، یعنی نتوانیم آن را به دو نیمه مساوی تقسیم کنیم، آن شکل نامتقارن خواهد بود، مانند شکل زیر که دو نیمه آن شبیه به هم نیست.
بهطور کلی، مفهوم تقارن به یکسان بودن شکل با شکل دیگر پس از جابهجایی و چرخش اشاره دارد.
اولین نفری باشید که از اخبار و اطلاعیه‌های مرتبط با پایه تحصیلیتان باخبر میشود!
انواع تقارن چیست؟
آشنایی با انواع تقارن، در درک و توصیف الگوها، اشکال و ساختارهای پیرامونمان به ما کمک میکند. انواع تقارن عبارت‌اند از
- تقارن انتقالی
- تقارن محوری یا بازتابی
- تقارن چرخشی
- تقارن مرکزی یا نقطهای
- تقارن لغزشی
تقارن انتقالی
اگر یک شکل را در یک جهت خاص و درامتداد یک خط مستقیم جابه‌جا کنیم، طوری که پس از جابهجایی، ظاهر آن بدون تغییر باقی بماند، شکل دارای تقارن انتقالی خواهد بود.
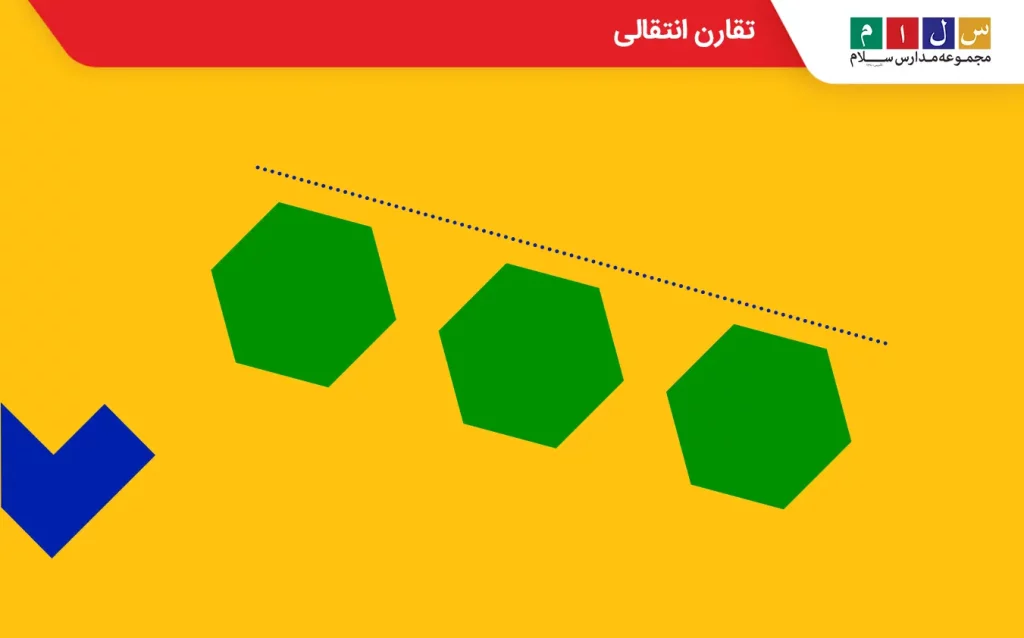
تقارن محوری
تقارن محوری که به آن تقارن بازتابی یا تقارن آینه‌ای هم می‌گویند، نوعی تقارن است که در آن نیمی از شکل بازتاب نیمه دیگر است. بنابراین، می‌توان گفت هر شکلی که تقارن محوری دارد، دارای خط تقارن نیز هست.
خط تقارن
خط تقارن یا محور تقارن خطی فرضی است که اگر از آن قسمت یک شکل را تا کنیم، دو نیمه شکل دقیقاً روی هم منطبق می‌شوند و همدیگر را می‌پوشانند. اشکالی که متقارن هستند می‌توانند یک یا چند خط تقارن داشته باشند. مثلاً تصویر زیر، یک شکل متقارن با دو خط تقارن را نشان می‌دهد.
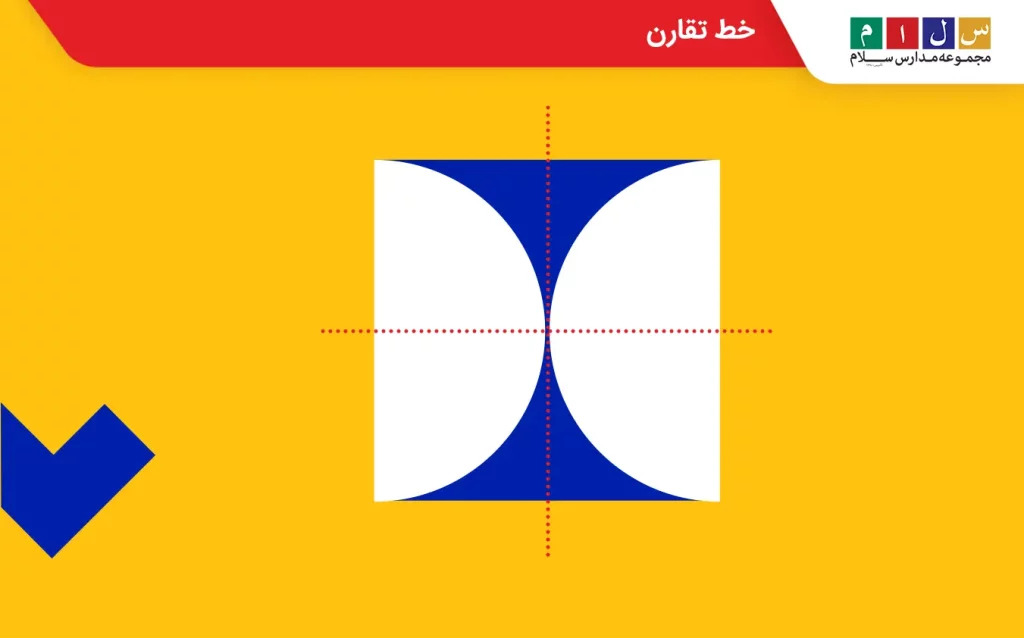
انواع خط تقارن
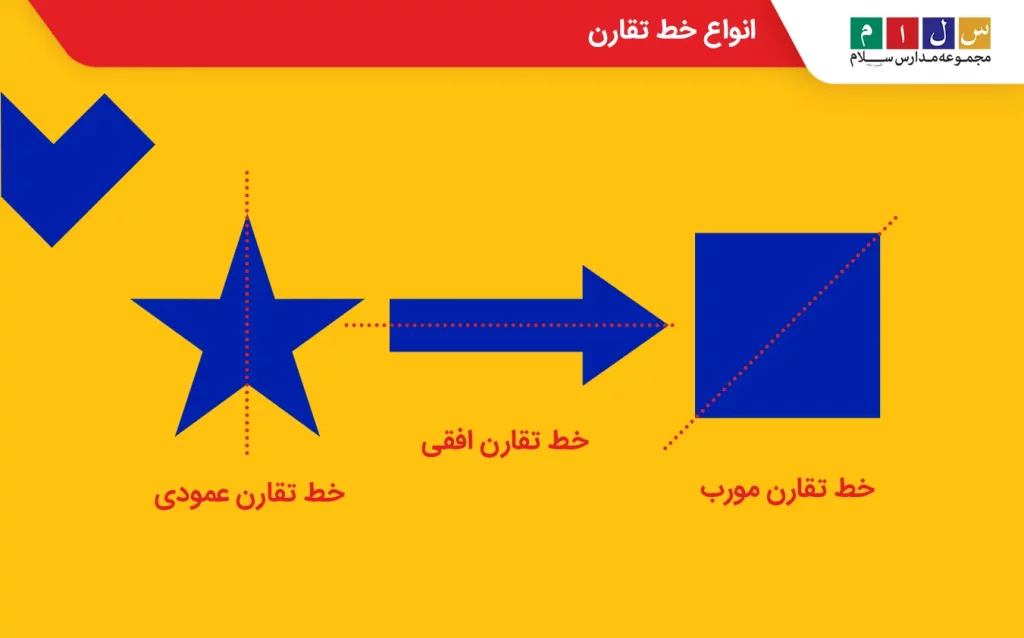
خط تقارن بسته به نوع جهت‌گیری به سه دسته تقسیم‌بندی میشود:
- خط تقارن افقی: یک خط افقی که شکل متقارن را به دو قسمت مساوی بالا و پایین تقسیم میکند.
- خط تقارن عمودی: خطی عمودی که شکل متقارن را به دو قسمت مساوی چپ و راست تقسیم میکند.
خط تقارن مورب: خطی مورب که شکل متقارن را به‌صورت مورب به دو قسمت مساوی تقسیم میکند.
تقارن چرخشی
اگر شکلی پس از چرخش به اندازه مشخص حول یک نقطه، به حالت اولیهاش بازگردد، گفته میشود که آن شکل دارای تقارن چرخشی است. برای مثال، اگر ستاره زیر را حول نقطه P بهاندازه معینی بچرخانیم، دوباره روی حالت اولیهاش منطبق میشود.
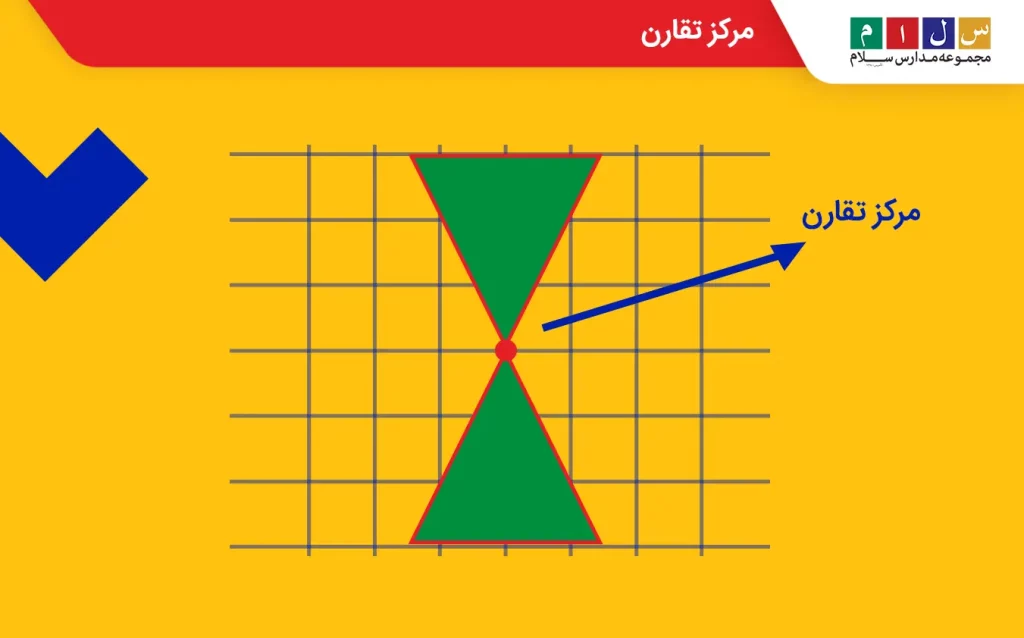
تقارن مرکزی
اگر یک شکل را بهاندازه نیمدور (۱۸۰ درجه) حول یک نقطه بچرخانیم، طوری که پس از چرخش، شکل روی خودش منطبق شود، میگوییم شکل تقارن مرکزی یا تقارن نقطهای دارد. درواقع، تقارن مرکزی نوعی تقارن چرخشی است. در تصویر زیر، تقارن مرکزی حرف F حول مبدأ نشان داده شده است.
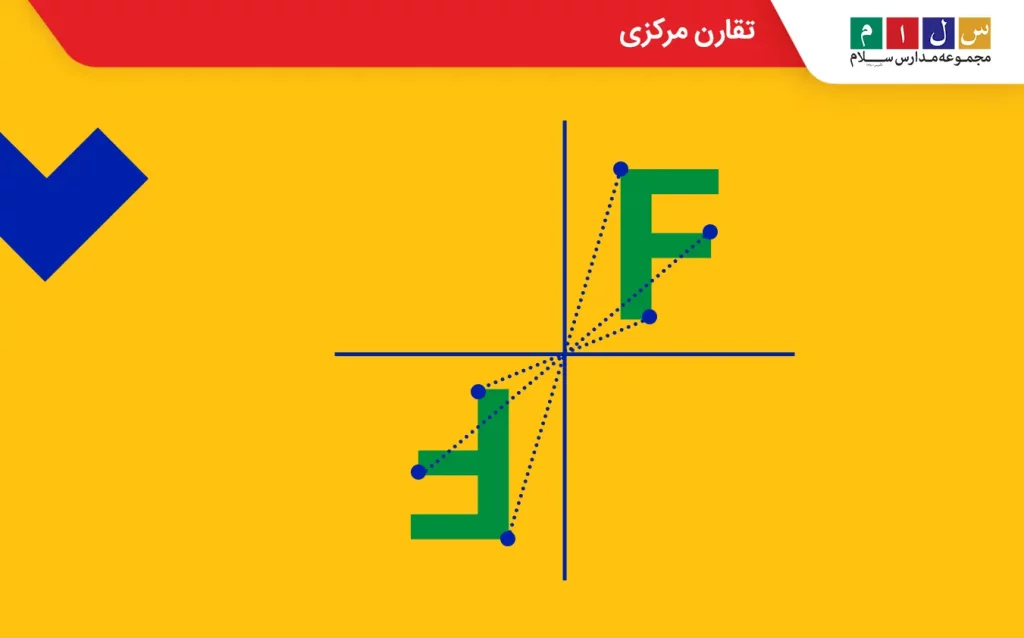
برای تشخیص اینکه آیا یک شکل تقارن مرکزی دارد یا خیر، می‌توانید از دو روش زیر استفاده کنید:
- شکل را ۱۸۰ درجه حول مرکز بچرخانید. اگر شکل پس از چرخش روی خودش منطبق شد، یعنی شکل موردنظر تقارن مرکزی دارد.
- نقاط مشابه را مانند شکل بالا به مرکز وصل کنید. اگر فاصله نقاط مشابه در دو طرف تا مرکز یکسان بود، یعنی آن شکل دارای تقارن مرکزی است.
مرکز تقارن
مرکز تقارن نقطهای است که اگر یک شکل را حول آن بهاندازه نیمدور بچرخانیم، روی خودش منطبق میشود و به حالت اولیهاش برمیگردد.
تقارن لغزشی
این نوع تقارن، ترکیبی از تبدیل انتقالی و بازتابی است و درمقایسه با انواع دیگر تقارن کمتر رایج است.
مثال هایی از تقارن
برای تشخیص بهتر تقارن در اشکال مختلف، درادامه چند مثال را با هم بررسی می‌کنیم.
مثال ۱: آیا شکل زیر تقارن محوری دارد؟
جواب: همان‌طور که می‌بینید، تنها یک خط تقارن مورب، شکل را به دو قسمت مشابه تقسیم میکند. اگر از این خط مورب شکل را تا کنیم، دو نیمه شکل کاملاً روی هم می‌افتند.
مثال ۲: کدام یک از حروف A، C، F و W تقارن محوری ندارد؟
جواب: با بررسی خط‌های تقارن افقی، عمودی و مورب این حروف، می‌توانیم مشخص کنیم که کدام یک تقارن محوری دارند.
همان‌طور که می‌بینید، تنها حرفی که تقارن محوری ندارد، حرف F است.
مثال ۳: آیا شکل زیر تقارن مرکزی دارد؟
جواب: شکل فوق تقارن مرکزی ندارد زیرا اگر آن را حول مبدأ نیمدور بچرخانیم، روی خودش منطبق نمی‌شود. در تصویر زیر، تقارن مرکزی این شکل را به‌صورت صحیح نشان داده‌ایم
مثال ۴: آیا ستاره چهاررأس، تقارن چرخشی ۹۰ درجه دارد؟
جواب: برای اینکه مشخص کنیم آیا این ستاره تقارن چرخشی ۹۰ درجه دارد یا خیر، باید آن را حول مرکزش بهاندازه ۹۰ درجه بچرخانیم. همان‌طور که در شکل زیر مشاهده می‌کنید، این ستاره پس از چرخش با اندازه موردنظر، روی خودش منطبق میشود. بنابراین، ستاره چهاررأس تقارن چرخشی ۹۰ درجه دارد.
پیشنهاد مطالعه: میانگین چیست؟
سخن پایانی
تقارن یکی از مفاهیم جذاب در ریاضیات است که به درک الگوها و ساختارهای مختلف کمک میکند. وقتی میگوییم یک شکل تقارن دارد منظورمان این است که می‌توان آن شکل را از وسط به دو قسمت مساوی و مشابه تقسیم کرد، طوری که اگر از یک خط فرضی آن را تا کنیم، دو نیمه کاملاً همدیگر را می‌پوشانند و روی هم منطبق می‌شوند. چنین شکلی را متقارن و خط فرضی آن را خط تقارن می‌گویند. تقارن انواع مختلفی دارد:
۱) اگر یک شکل به دو قسمت مساوی تقسیم شود و یک نیمه آن بازتاب نیمه دیگر باشد، آن شکل تقارن محوری دارد.
۲) اگر شکل پس از چرخش ۱۸۰ درجه حول یک نقطه به حالت اولیه خود بازگشت، آن شکل دارای تقارن مرکزی خواهد بود.
۳) اگر یک شکل را درامتداد یک خط مستقیم جابه‌جا کنیم، طوری که پس از جابهجایی، بدون تغییر باقی بماند، میگوییم شکل تقارن انتقالی دارد.
۴) اگر یک شکل را حول یک نقطه بهاندازه معینی دوران دهیم، بهگونهای که پس از دوران روی خودش منطبق شود، شکل تقارن چرخشی خواهد داشت.
سؤالات متداول
- تقارن یعنی چه؟
در ریاضیات، اگر یک شکل را بتوانیم به دو نیمه مساوی و مشابه تقسیم کنیم، بهگونهای که اگر شکل را از یک خط فرضی (خط تقارن) تا کنیم، دو نیمه شکل روی هم منطبق شوند، میگوییم شکل تقارن دارد. اما بهطور کلی، تقارن به یکسان بودن شکل با شکلی دیگر پس از جابهجایی و چرخش اشاره دارد. - انواع تقارن کدام است؟
تقارن محوری، تقارن چرخشی، تقارن مرکزی، تقارن انتقالی، تقارن لغزشی - تقارن محوری چیست؟
نوعی تقارن است که در آن نیمه یک شکل بازتاب نیمه دیگر است. - خط تقارن چیست؟
خطی است که یک شکل را به دو قسمت مساوی و قرینه تقسیم میکند. - تقارن چرخشی چیست؟
نوعی تقارن است که در آن شکل پس از چرخش بهاندازه معین حول یک نقطه مرکزی، به حالت اولیه خود برمیگردد. - تقارن مرکزی چیست؟
در این نوع تقارن، شکل پس از چرخش بهاندازه نیمدور (۱۸۰ درجه) حول یک نقطه مرکزی، روی خودش منطبق میشود. - مرکز تقارن چیست؟
نقطهای است که شکل پس از دوران ۱۸۰ درجه حول آن، به حاالت اولیهاش برمیگردد.
