قضیه فیثاغورس به زبان ساده ׀ اثبات به ۳ روش + کاربردهای آن

بیش از ۲۰۰۰ سال پیش، یک فیلسوف و ریاضی‌‌دان یونانی به‌‌نام «فیثاغورس» کشف شگفت‌‌انگیزی درمورد مثلث‌‌ها انجام داد که به قضیه فیثاغورس (یا فیثاغورث) معروف شد و از دوران باستان تاکنون برای حل مسائلی که در آن مثلث قائم الزاویه به‌‌کار می‌‌رود، مورد استفاده قرار گرفته است. این قضیه به ما این امکان را می‌‌دهد تا طول هر ضلع در یک مثلث قائم‌‌الزاویه را محاسبه کنیم. در این آموزش، سعی می‌‌کنیم اثبات قضیه فیثاغورس هندسه دهم و عکس آن را برایتان توضیح دهیم و شما را با کاربرد فیثاغورس در زندگی آشنا کنیم.

مثلث قائم الزاویه چیست ؟

مثلث قائم‌‌الزاویه مثلثی است که یکی از سه زاویه داخلی آن قائمه یا ۹۰ درجه است. ضلعی که مقابل زاویه ۹۰ درجه قرار می‌‌گیرد، وتر مثلث و دو ضلع دیگر که بر هم عمودند و زاویه قائمه را می‌‌سازند، اضلاع مجاور زاویه قائمه یا ساق نام دارند. وتر طولانی‌‌ترین ضلع این مثلث است.

قضیه فیثاغورس چیست ؟

اگر یک مثلث قائم‌‌الزاویه مانند تصویر زیر داشته باشیم (مثلث خاکستری‌‌رنگ در وسط) و با استفاده از اضلاع آن مربع‌‌هایی بسازیم، مساحت بزرگ‌‌ترین مربع ساخته‌‌شده روی وتر (طولانی‌‌ترین ضلع مثلث) برابر است با مجموع مساحت‌‌های مربع‌‌های ساخته‌‌شده روی دو ضلع دیگر.

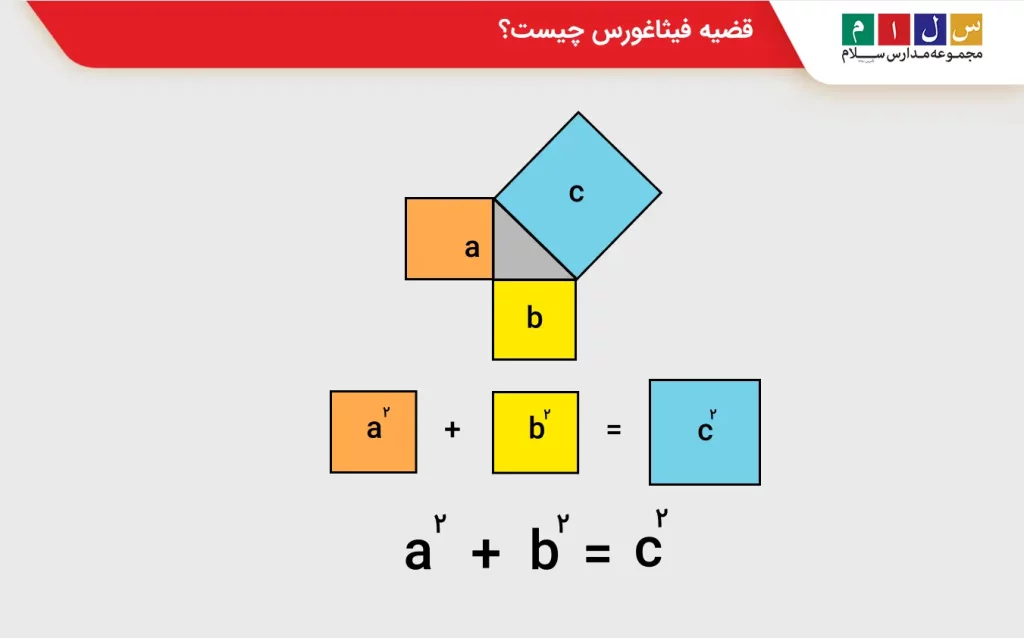
بنابراین، قضیه فیثاغورس را می‌‌توان اینگونه بیان کرد: مربعِ بزرگ‌‌ترین ضلع یک مثلث قائم‌‌الزاویه (یعنی وتر) برابر با مجموع مربعات دو ضلع دیگر است.

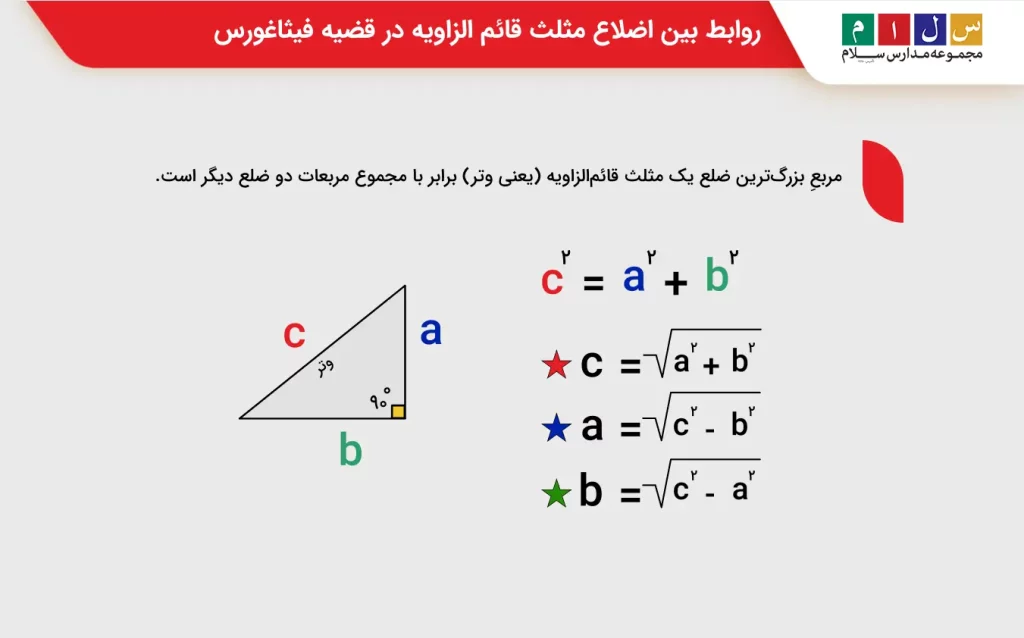
به‌‌طور کلی، قضیه فیثاغورس سه ضلع یک مثلث قائم‌‌الزاویه را به هم مرتبط می‌‌کند. به این صورت که اگر طول دو ضلع یک مثلث قائم‌‌الزاویه را بدانیم، می‌‌توانیم طول ضلع سوم را تعیین کنیم. تصویر زیر روابط بین اضلاع مثلث قائم‌‌الزاویه را به‌‌خوبی نشان می‌‌دهد.

قضیه فیثاغورس به صورت دو شرطی

هرگاه یک قضیه و عکس آن هر دو برقرار باشند، آنگاه آن قضیه را قضیه دوشرطی می‌‌نامند. قضیه فیثاغورس نیز یک قضیه دوشرطی است چرا که هم خود قضیه و هم عکس آن درست است. این قضیه دوشرطی به‌‌صورت زیر بیان می‌‌شود:

«یک مثلث قائم‌‌الزاویه است اگر و تنها اگر مربع (مجذور) ضلع مقابل به زاویه قائمه (وتر) برابر با مجموع مربعات دو ضلع دیگر باشد.»

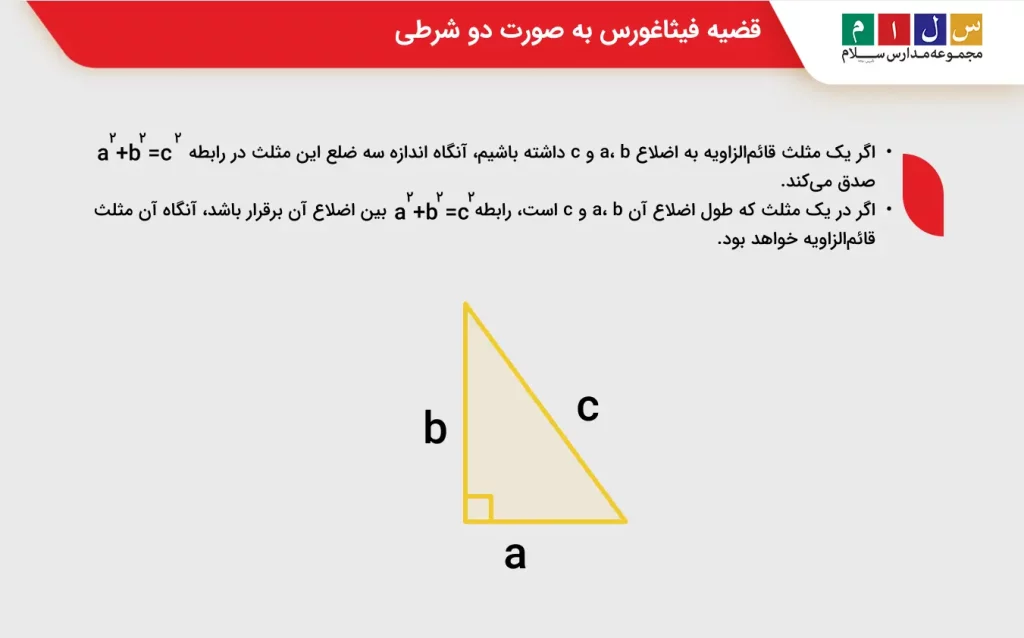
با توجه به شکل زیر، از این قضیه می‌‌توان دو گزاره زیر را نتیجه گرفت:

• اگر یک مثلث قائم‌‌الزاویه به اضلاع a، b و c داشته باشیم، آنگاه اندازه سه ضلع این مثلث در رابطه a^۲+b^۲=c^۲ صدق می‌‌کند.
• اگر در یک مثلث که طول اضلاع آن a، b و c است، رابطه a^۲+b^۲=c^۲ بین اضلاع آن برقرار باشد، آنگاه آن مثلث قائم‌‌الزاویه خواهد بود.

اثبات قضیه فیثاغورس

قضیه فیثاغورس را می‌‌توان به رو‌‌ش‌‌های مختلفی اثبات کرد. در اینجا ما سه روش رایج برای اثبات قضیه فیثاغورس هشتم آورده‌‌ایم.

اثبات قضیه فیثاغورس با تشابه

یک مثلث قائم‌‌الزاویه ABC مانند شکل زیر در نظر بگیرید که زاویه قائمه آن در رأس B قرار دارد. از رأس B یک پاره‌‌خط عمود بر ضلع مقابلش یعنی AC رسم می‌‌کنیم و محل برخورد خط عمود و ضلع AC را D می‌‌نامیم.

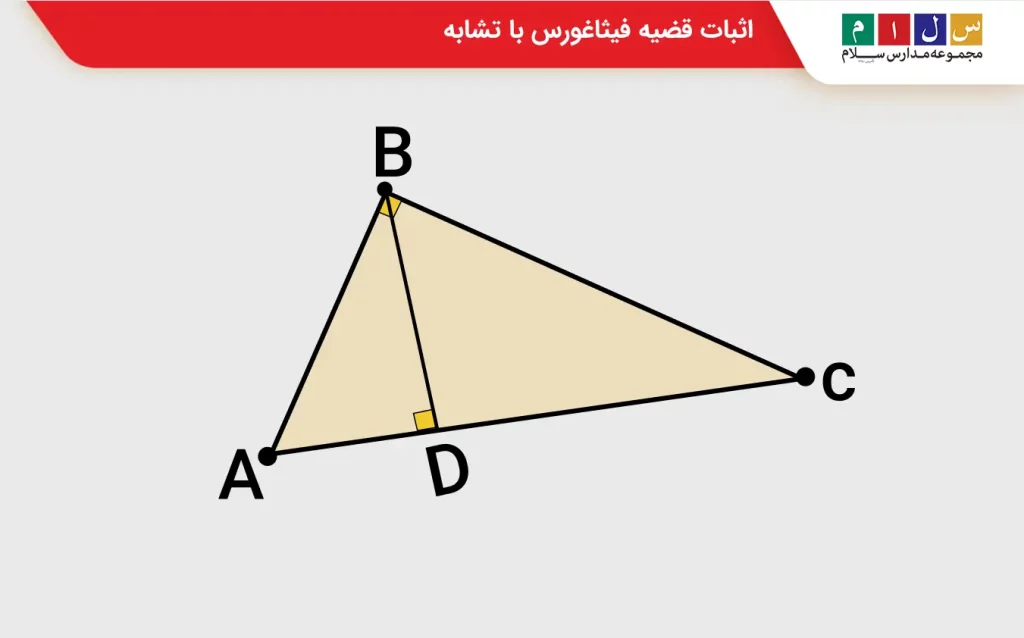
همان‌‌طور که می‌‌بینید، در مثلث‌‌های ABD و ACB زاویه A مشترک است و زوایای ADB و ABC نیز هر دو قائمه هستند. بنابراین، دو مثلث ABD و ACB به‌‌دلیل داشتن دو زاویه شبیه به هم، مشابه یکدیگرند. از این تشابه می‌‌توان نتیجه گرفت:

تشابه مثلث‌‌های BCD و ACB نیز به همین صورت اثبات می‌‌شود. در این مثلث‌‌ها زاویه C مشترک بوده و دو زاویه BDC و ABC نیز قائمه‌‌اند. از این تشابه می‌‌توان به تساوی زیر رسید:

با جمع کردن دو معادله بالا خواهیم داشت:

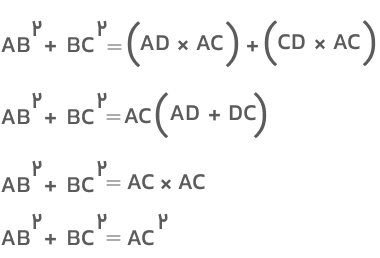
رابطه به‌‌دست‌‌آمده همان قضیه فیثاغورس را نشان می‌‌دهد.

اثبات قضیه فیثاغورس با مساحت ذوزنقه

یکی از راه‌‌های اثبات قضیه فیثاغورس استفاده از مساحت ذوزنقه است. این روش اثبات را به‌‌صورت زیر انجام می‌‌دهیم:

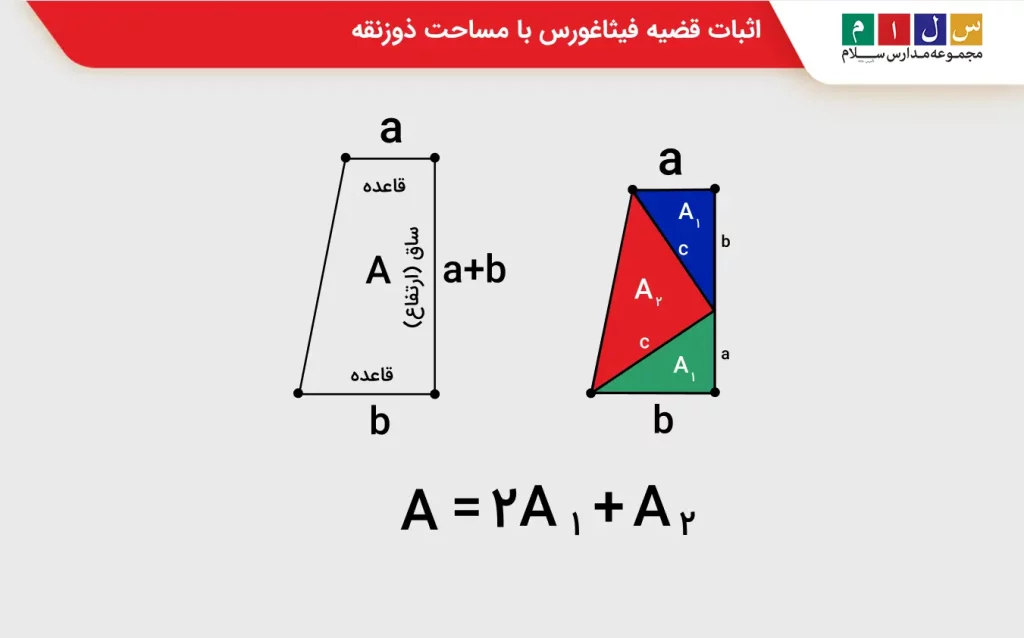
۱. یک ذوزنقه قائم الزاویه به‌‌شکل زیر رسم می‌‌کنیم که قاعده‌‌های آن a و b و ارتفاع (ساق عمود بر قاعده‌‌های) آن a + b است.

۲. ذوزنقه را به سه مثلث قائم‌‌الزاویه که دو تای آن‌‌ها با هم برابرند تقسیم می‌‌کنیم. به این صورت که ساق عمود را به طول‌‌های a و b تقسیم کرده تا دو مثلث مشابه به اضلاع a، b و c ایجاد شود. با این تقسیم‌‌بندی، مثلث سومی که به‌‌وجود می‌‌آید دو ضلع برابر به طول c خواهد داشت.

۳. حالا با استفاده از فرمول مساحت ذوزنقه، مساحت ذوزنقه قائم‌‌الزاویه را به‌‌صورت زیر محاسبه می‌‌کنیم:

• قاعده‌‌ها: a و b
• ارتفاع: a + b
• مساحت: A

۴. در این مرحله، مساحت ذوزنقه را از مجموع مساحت سه مثلثی که ذوزنقه را تشکیل می‌‌دهند به‌‌دست می‌‌آوریم. ابتدا مساحت سه مثلث را حساب می‌‌کنیم. با توجه به اینکه دو تا از مثلث‌‌ها برابرند، مساحت آن‌‌ها هم یکسان خواهد بود. کافی‌‌ست مساحت یک مثلث را محاسبه کرده و در دو ضرب کنیم. مساحت یک مثلث با قاعده a و ارتفاع b از فرمول زیر به‌‌دست می‌‌آید:

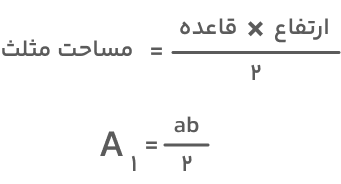
بنابراین، مساحت دو مثلث مشابه برابر است با

۲A_۱=ab

فرمول مساحت مثلث سوم نیز که اندازه دو ضلع آن مساوی با c است به‌‌صورت زیر خواهد بود:

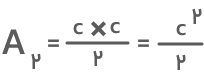
اکنون می‌‌توانیم با جمع کردن مساحت سه مثلث، مساحت ذوزنقه را به‌‌دست آوریم:

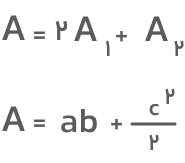
۵. در آخر، مساحت به‌‌دست‌‌آمده از مرحله ۳ را با مجموع مساحت سه مثلث مساوی قرار می‌‌دهیم زیرا هر دو رابطه مساحت ذوزنقه را نشان می‌‌دهند.

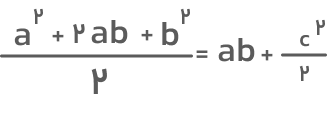
طرفین تساوی را در دو ضرب می‌‌کنیم:

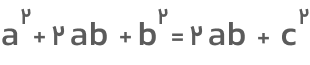
داریم:

a^۲+b^۲=c^۲

همان‌‌طور که می‌‌بینید، این تساوی همان تساوی معروف در قضیه فیثاغورس است.

ساده ترین راه اثبات قضیه فیثاغورس

تا اینجا با دو روش اثبات قضیه فیثاغورس آشنا شدیم. در این بخش می‌‌خواهیم از روش ساده‌‌تر و معروف‌‌تری که با کمک مساحت مربع انجام می‌‌شود استفاده کنیم. اثبات به این روش طی چند مرحله زیر صورت می‌‌گیرد.

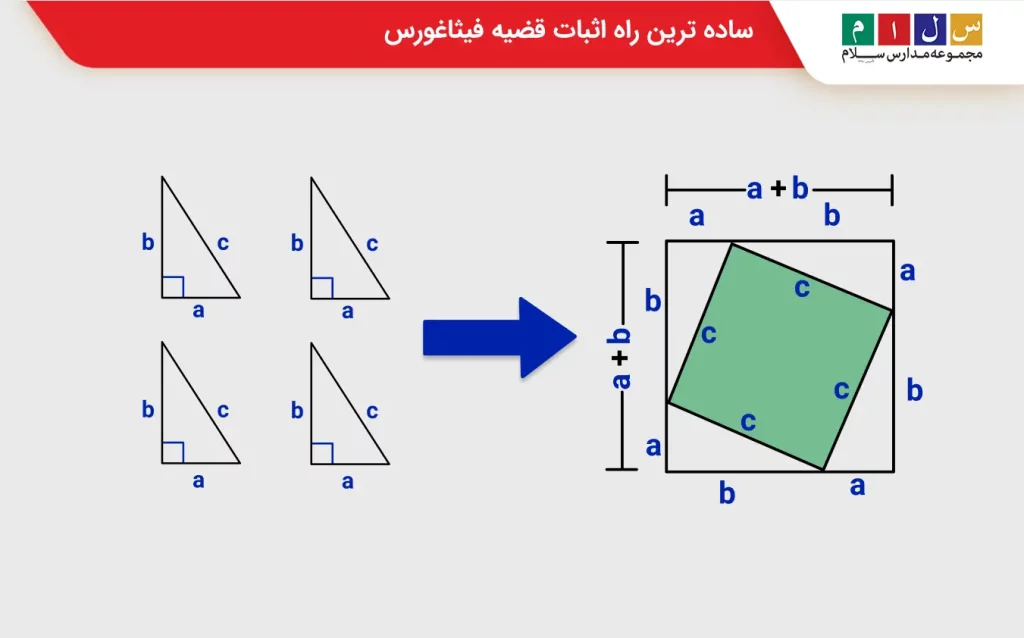
• ابتدا مطابق تصویر، چهار مثلث قائم‌‌الزاویه مشابه به اضلاع a، b و c رسم می‌‌کنیم.
• مثلث‌‌ها را طوری کنار هم قرار می‌‌دهیم که وترهای آن‌‌ها مربع کوچک‌‌تری به ضلع c و ساق‌‌هایشان مربع بزرگ‌‌تری به ضلع a + b تشکیل دهند. اگر کل چیدمان را ۹۰ درجه بچرخانیم، تغییری در شکل ایجاد نخواهد شد.
• مساحت مربع بزرگ برابر با a+b)^۲) و مساحت مربع کوچک برابر با c^۲ است. اگر مساحت مربع کوچک‌‌تر را از مساحت مربع بزرگ‌‌تر کم کنیم، مساحت چهار مثلث قائم‌‌الزاویه به‌‌دست می‌‌آید که با تقسیم آن بر عدد ۴ می‌‌توان مساحت یک مثلث قائم‌‌الزاویه را محاسبه کرد.

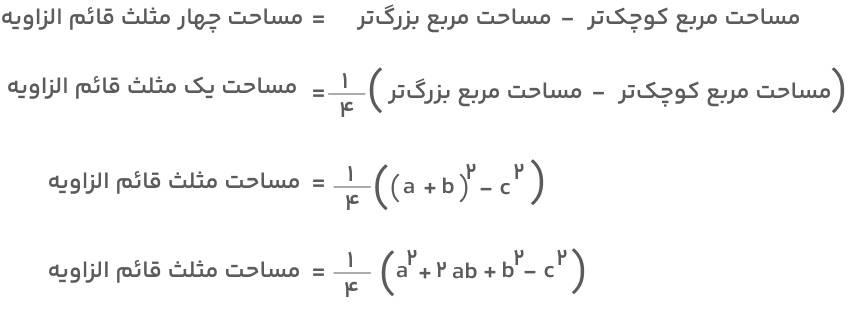
ازطرفی می‌‌دانیم که مساحت هر کدام از این مثلث‌‌ها از فرمول زیر به‌‌دست می‌‌آید:

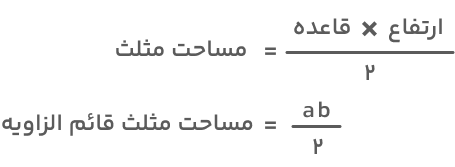
هر دو رابطه به‌‌دست‌‌آمده برای محاسبه مساحت مثلث قائم‌‌الزاویه مقدار یکسانی به ما می‌‌دهند. پس می‌‌توانیم آن‌‌ها را مساوی هم قرار دهیم:

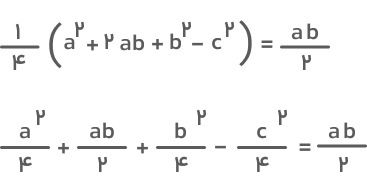
اگر جمله‌‌های مساوی در طرفین را حذف کنیم، خواهیم داشت:

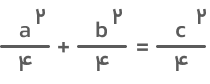
درنتیجه

a^۲+b^۲=c^۲

به همین راحتی توانستیم به فرمول قضیه فیثاغورس برسیم و آن را اثبات کنیم.

اثبات عکس قضیه فیثاغورس

عکس قضیه فیثاغورس بیان می‌‌کند که اگر مربع طول بزرگ‌‌ترین ضلع یک مثلث برابر با مجموع مربعات طول دو ضلع دیگر باشد، آن مثلث قائم‌‌الزاویه است. براین‌‌اساس، اگر یک مثلث به ما داده شود و طول هر سه ضلع آن مشخص باشد، می‌‌توانیم با استفاده از عکس قضیه فیثاغورس بررسی کنیم که آیا مثلث موردنظر، قائم‌‌الزاویه است یا خیر.

ثابت کنیم که در این مثلث زاویه B برابر با ۹۰ درجه است.

اثبات این قضیه بسیار ساده است. مثلث ABC در شکل زیر را در نظر بگیرید که طبق عکس قضیه فیثاغورس رابطه برای اثبات، ابتدا یک مثلث به‌‌نام PQR رسم می‌‌کنیم طوری‌‌که زاویه Q در آن قائمه و PQ=AB و QR=BC باشد. از مثلث PQR داریم:

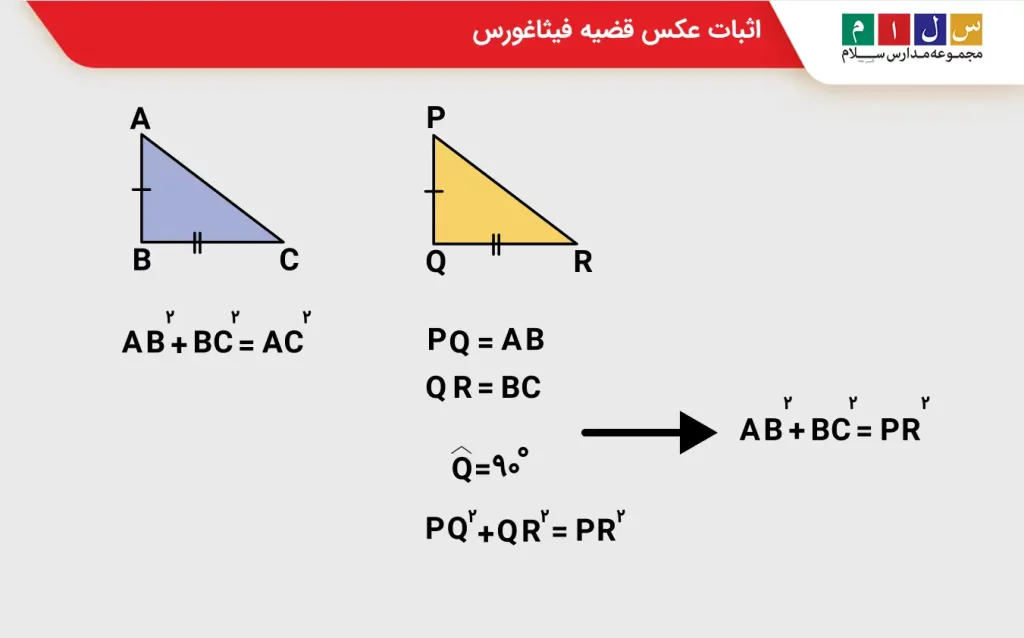
Q^{^}=۹۰°

PQ^۲+QR^۲=PR^۲

یا

AB^۲+BC^۲=PR^۲

ازطرفی، در مثلث ABC نیز رابطه زیر را داریم:

AB^۲+BC^۲=AC^۲

پس نتیجه می‌‌گیریم که

AC=PR

براین‌‌اساس، می‌‌توان گفت دو مثلث ABC و PQR در حالت ض‌‌ض‌‌ض هم‌‌نهشت هستند. از هم‌‌نهشت بودن دو مثلث و قائمه بودن زاویه Q به نتیجه زیر می‌‌رسیم:

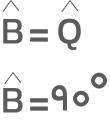
این نشان می‌‌دهد که مثلث ABC قائم‌‌الزاویه است و به این صورت عکس قضیه فیثاغورس اثبات می‌‌شود.

درادامه یک مثال حل کنیم تا کاربرد عکس قضیه فیثاغورس را بهتر یاد بگیرید.

مثال: یک مثلث اضلاعی به طول ۵، ۱۲ و ۱۴ سانتی‌‌متر دارد. بررسی کنید که آیا این مثلث قائم‌‌الزاویه است یا خیر.
جواب: طبق عکس قضیه فیثاغورس، ابتدا باید مربع اضلاع را به‌‌دست آوریم:

۵^۲=۲۵
۱۲^۲=۱۴۴
۱۴^۲=۱۹۶

اکنون باید بررسی کنیم که آیا مربع بزرگ‌‌ترین ضلع مثلث برابر با مجموع مربع دو ضلع دیگر است یا نه.

۲۵ + ۱۴۴ = ۱۶۹

ازآنجا که است، مثلث موردنظر قائم‌‌الزاویه محسوب نمی‌‌شود.

کاربرد قضیه فیثاغورس

کاربردهای قضیه فیثاغورس را می‌‌توان در زندگی روزمره مشاهده کرد. در اینجا به برخی از کاربردهای قضیه فیثاغورس اشاره می‌‌کنیم.

• حمل‌‌ونقل جاده‌‌ای

از قضیه فیثاغورس می‌‌توان برای یافتن حداقل فاصله بین دو نقطه و طراحی مسیر براساس آن برای داشتن حداقل زمان حمل‌‌ونقل استفاده کرد. بخش تحویل پست و لجستیک از این قضیه برای یافتن حداقل فاصله بین نقاط تحویل و سپس انتخاب کوتاه‌‌ترین مسیرها از بین مسیرهای موجود برای کاهش هزینه‌‌های سوخت و بهبود دوره‌‌های سرویس‌‌دهی آن‌‌ها استفاده می‌‌کنند.

• خطوط هوایی

قضیه فیثاغورس در خطوط هوایی برای طراحی باند فرودگاه‌‌ها جهت برخاستن و فرود ایمن هواپیماها به‌‌کار می‌‌رود. همچنین خلبان‌‌ها از این قضیه برای محاسبه کوتاه‌‌ترین مسیر مستقیم بین نقاط مسیر در یک فضای سه‌‌بعدی استفاده می‌‌کنند و مسیرهای پرواز را براساس آن برنامه‌‌ریزی می‌‌کنند تا سوخت صرفه‌‌جویی شود و زمان سفر کاهش یابد.

• رباتیک

الگوریتم‌‌های ناوبری برای ربات‌‌ها با استفاده از قضیه فیثاغورس طراحی شده‌‌اند تا ناوبری کارآمد تضمین شده و کوتاه‌‌ترین مسیر با در نظر گرفتن موانع مختلف در مسیر، دنبال شود. ربات‌‌ها می‌‌توانند با محاسبه فاصله افقی و عمودی بین سطوح، کوتاه‌‌ترین فاصله بین دو نقطه را پیدا کنند و سپس با استفاده از قضیه فیثاغورس، فاصله مورب موردنظر برای حرکت کارآمد و صرفه‌‌جویی در باتری را محاسبه کنند.

• مکانیک

تحلیل سازه‌‌ها برای محاسبه نیروها و تنش‌‌ها و سازه‌‌های مختلف مانند پل‌‌ها، ساختمان‌‌ها، روگذرها و غیره جهت اطمینان از پایداری و ایمنی با کمک قضیه فیثاغورس می‌‌تواند انجام شود.

• الکترونیک

در الکترونیک برای محاسبه کوتاه‌‌ترین مسیر جهت اتصال اجزا در طراحی بردهای مدار چاپی به‌‌منظور کاهش مقاومت و بهینه‌‌سازی عملکرد کلی مدار این قضیه کاربرد دارد. همچنین برای تعیین ارتفاع و موقعیت بهینه آنتن‌‌ها با محاسبه فاصله آن‌‌ها از گیرنده جهت به‌‌حداکثر رساندن قدرت سیگنال و سطح پوشش استفاده می‌‌شود.

نمونه سوال کاربرد قضیه فیثاغورس

حالا که با این قضیه پرکاربرد آشنا شدیم، خوب است به حل چند مثال برای قضیه فیثاغورث بپردازیم.

سؤال ۱: طول اضلاع مثلثی ۸، ۱۰ و ۶ سانتی‌‌متر است. آیا این مثلث قائم‌‌الزاویه است؟ اگر چنین است، وتر کدام ضلع است؟
جواب: می‌‌دانیم که وتر طولانی‌‌ترین ضلع در یک مثلث است. بنابراین، وتر مثلث همان ضلع ۱۰ سانتی‌‌متری است. برای اینکه مشخص شود آیا این مثلث زاویه قائمه دارد یا خیر، از قضیه فیثاغورس استفاده می‌‌کنیم.

۱۰^۲=۶^۲+۸^۲

۱۰۰=۳۶+۶۴

۱۰۰=۱۰۰

دو طرف تساوی برابر شد. این نشان می‌‌دهد که مثلث زاویه قائمه دارد.

سؤال ۲: قطر مربع زیر برابر با ۲√۲ است. مساحت آن را بیابید.

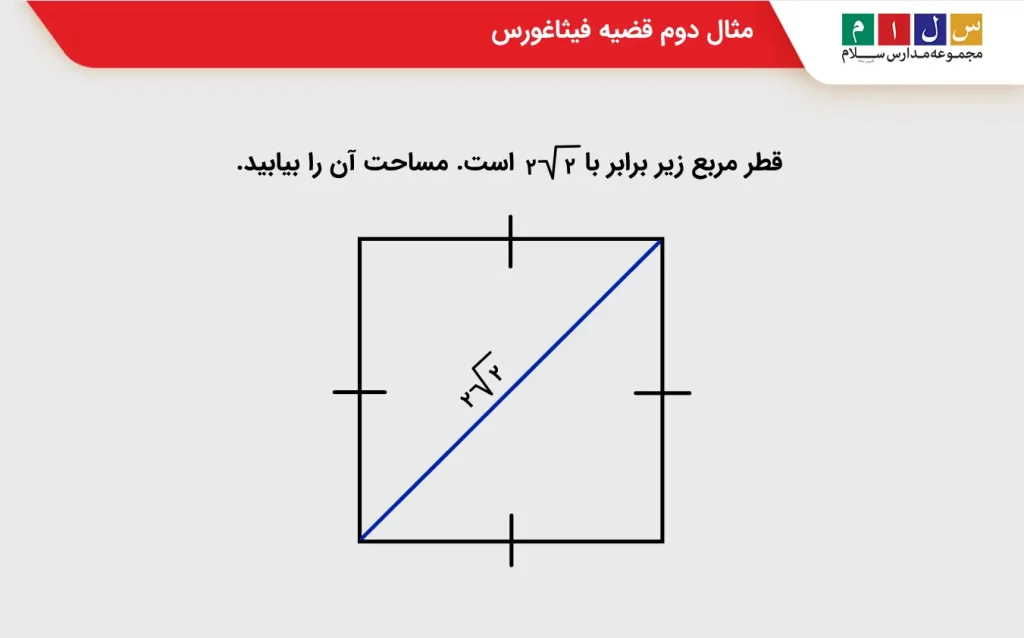
جواب: می‌‌دانیم که مساحت مربع از حاصل‌‌ضرب ضلع آن در خودش به‌‌دست می‌‌آید. با توجه به اینکه مربع اضلاع برابر دارد و قطر آن با دو ضلعش یک مثلث قائم‌‌الزاویه می‌‌سازد، می‌‌توانیم از قضیه فیثاغورس کمک بگیریم. فرض می‌‌کنیم ضلع مربع a است. در این صورت طبق قضیه فیثاغورس خواهیم داشت:

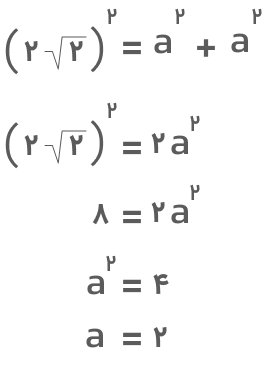
اکنون که اندازه ضلع مربع را یافتیم، می‌‌توانیم مساحت آن را تعیین کنیم:

A=a^۲=۲^۲=۴

پیشنهاد مطالعه: قطر چیست؟

سؤال ۳: طول ساق مثلث زیر را حساب کنید.

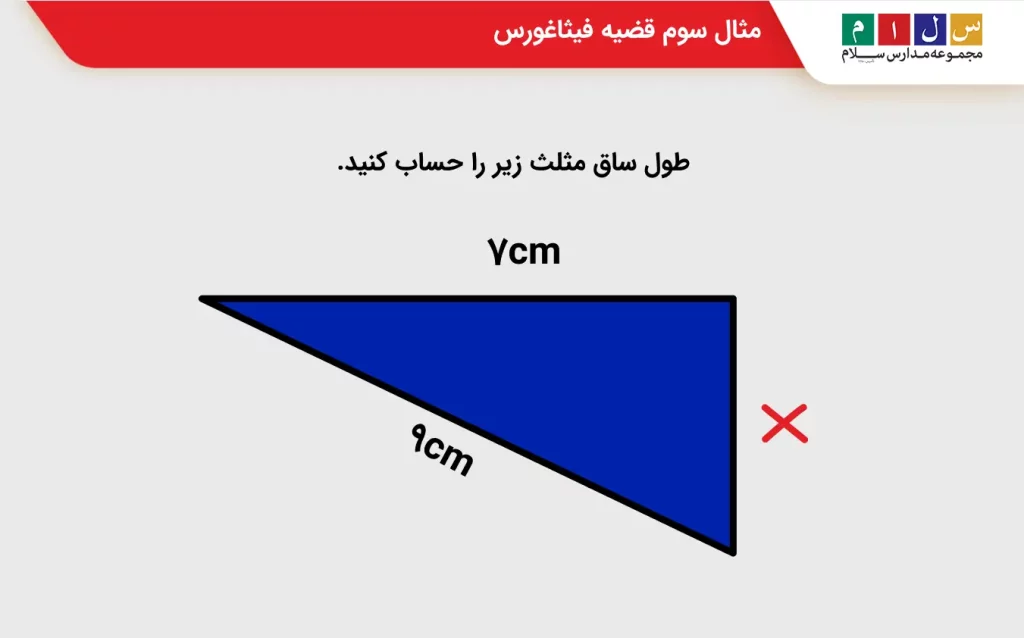
جواب: مثلث بالا یک مثلث قائم‌‌الزاویه است. کافی‌‌ست از فرمول قضیه فیثاغورس برای محاسبه ضلع مجهول آن استفاده کنیم:

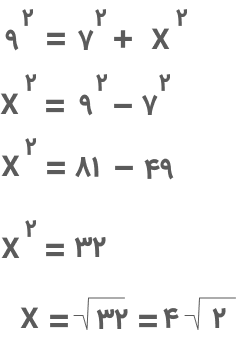
سؤال ۴: قطر مستطیل زیر چقدر است؟

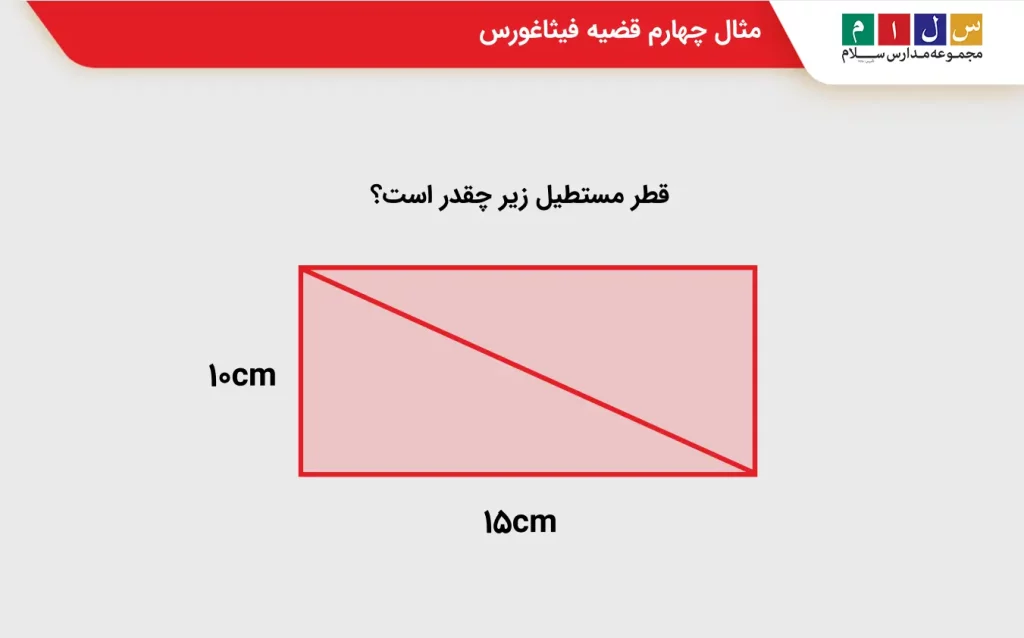
جواب: قطر مستطیل، مستطیل را به دو مثلث قائم‌‌الزاویه یکسان تقسیم می‌‌کند و به‌‌عبارتی، وتر مثلث‌‌ها محسوب می‌‌شود. اگر طول قطر را x در نظر بگیریم، با استفاده از قضیه فیثاغورس خواهیم داشت:

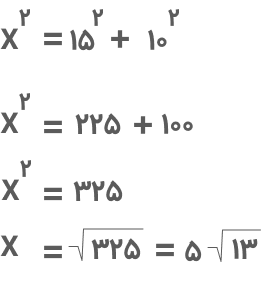
طول قطر۱۳√۵ سانتی‌‌متر است.

سؤال ۵: با توجه به شکل زیر مقدار x را به‌‌دست آورید.

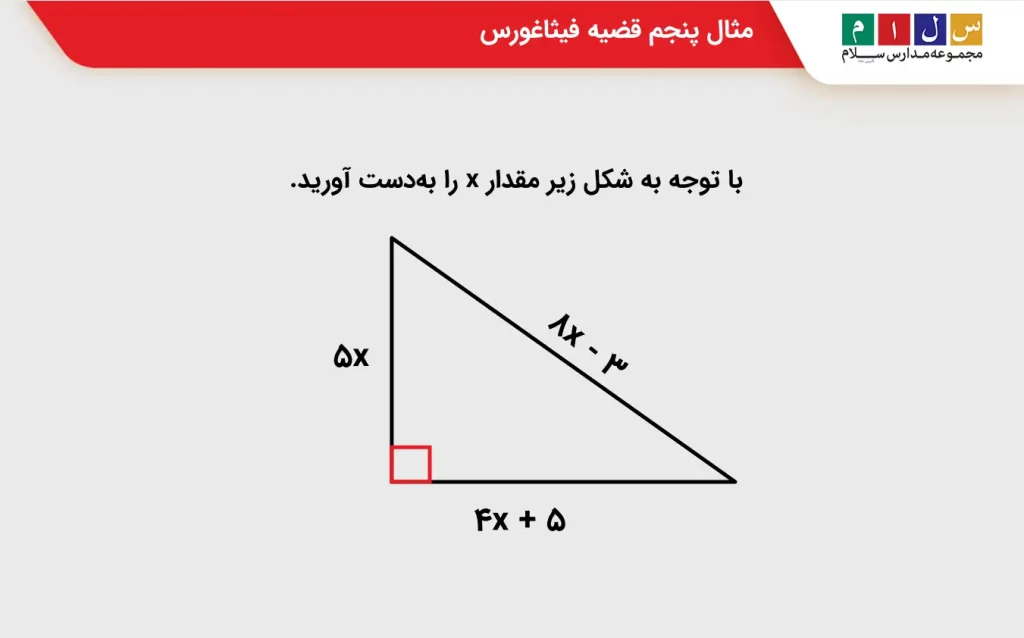
جواب: ازآنجا که یکی از سه زاویه مثلث قائمه است، برای تعیین مقدار x می‌‌توانیم قضیه فیثاغورس را به‌‌کار ببریم:

ساده‌‌سازی تساوی را با کمک اتحاد مربع انجام می‌‌دهیم:

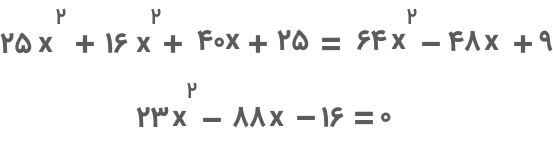
عبارت ساده‌‌شده یک معادله درجه دوم است و پاسخ آن را می‌‌توان با روش‌‌های مختلف محاسبه کرد. جواب‌‌های این معادله برابر است با

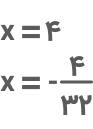
می‌‌دانیم طول ضلع همواره مقداری مثبت است. بنابراین، تنها جوابی که مقدار اضلاع را مثبت می‌‌کند و قابل‌‌قبول است x=۴ است.

سخن پایانی

قضیه فیثاغورس یکی از قضایای معروف و کاربردی در هندسه و ریاضی است که در این مقاله به آن پرداخته شد. در این آموزش با این قضیه و کاربردهای آن آشنا شدیم و دیدیم که به‌‌راحتی قضیه فیثاغورس اثبات می‌‌شود. علاوه‌‌بر اثبات، با حل مثال‌‌های مختلف کاربرد این قضیه در حل مسائل گوناگون را نیز یاد گرفتیم. اگر به اطراف خود خوب نگاه کرده و حرفه‌‌های مختلف را بررسی کنید خواهید دید که قضیه فیثاغورس کاربردهای زیادی در زندگی ما دارد و یادگیری آن از اهمیت بسیاری برخوردار است.