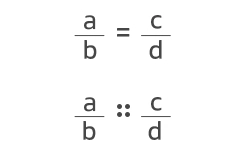فهرست مطالب
Toggleدر آموزشهای پیشین، در مورد مفهوم نسبت و نسبت های مساوی صحبت کردیم و گفتیم که اصطلاح نسبت را برای مقایسه دو چیز با واحدهای یکسان بهکار میبرند. همچنین توضیح دادیم که اگر دو یا چند نسبت با هم مساوی باشند، آنها را نسبتهای مساوی میگوییم. حالا در این مقاله، قصد داریم به موضوعی در ارتباط با همین مفاهیم یعنی تناسب در ریاضی بپردازیم و نحوه تشکیل جدول تناسب در مسائل گوناگون را همراه با حل مثال آموزش دهیم.
تناسب در ریاضی چیست؟
تناسب در ریاضی عمدتاً بر اساس نسبت یا همان کسر توضیح داده میشود. در آموزشهای پیشین دیدیم که نسبت دو کمیت a و b را میتوان به شکل کسری a /b نمایش داد.
مثلا، اگر در یک کلاس ۵۰ نفری، ۲۷ دانشآموز دختر و بقیه پسر باشند، نسبت تعداد دانشآموزان دختر به کل دانشآموزان این کلاس ۲۷ به ۵۰ یا ۲۷/۵۰ است.
در واقع، تناسب در ریاضی با نسبتهای مساوی در ارتباط است و هر دو نسبت مساوی یک تناسب تشکیل میدهند.
تعریف تناسب در ریاضی
در ریاضی، تناسب به معنای برابری دو نسبت (یا کسر) است. بهعبارت دیگر، اگر دو نسبت یا دو کسر با هم برابر باشند، میگوییم با هم تناسب دارند. بنابراین، تناسب معادلهای است که مساوی بودن نسبتها یا کسرها را نشان میدهد.
در ریاضی معمولاً از دو علامت “::” یا “=” برای نشان دادن تناسب استفاده میشود، البته در حل مسائل ریاضی اغلب نماد دوم یعنی “=” را بهکار میبرند. برای مثال، تناسب دو کسر را میتوان به دو صورت زیر نمایش داد:
علامت “=” بین دو کسر، نشاندهنده مساوی بودن دو کسر است. این مفهوم به ما کمک میکند تا در مسائل مربوط به تناسب به معادلهای برسیم که بتوانیم با استفاده از آن مقادیر نامعلوم را بهدست آوریم. برای آشنایی با فرمول تناسب در مسائل ریاضی به مثال زیر توجه کنید.
فرض کنید یک تساوی بهصورت زیر داریم:
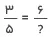
کسر اول نسبت ۳ به ۵ را نشان میدهد اما کسر دوم بهدلیل نامعلوم بودن مقدار مخرج مشخص نیست چه نسبتی را نشان میدهد. بنابراین، باید ببینیم نسبت ۳ به ۵ با نسبت ۶ به چه عددی تناسب میسازد. در ریاضی معمولاً برای نشان دادن مقدار مجهول در چنین معادلههایی بهجای “؟” از حروف انگلیسی مانند x استفاده میکنیم و با روشی که در ادامه آموزش خواهیم داد مقدار آنها را بهدست میآوریم.
پیشنهاد مطالعه: ثلث در ریاضی چیست؟
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
تناسب مسلسل
فرض کنید سه نسبت (یا کسر) داریم. اگر نسبت اول و دوم با هم تناسب داشته باشند و بین نسبت دوم و سوم نیز تناسب وجود داشته باشد، آنگاه بین نسبتهای اول و سوم نیز تناسب برقرار خواهد بود. چنین تناسبی را «تناسب مسلسل» مینامیم. این حالت را برای بیشتر از سه نسبت نیز میتوانیم داشته باشیم.
بهعنوان مثال، فرض کنید سه نسبت را داریم. اگر
باشد، آنگاه
خواهد بود.
چند نکته درباره تناسب
در ادامه، چند نکته کاربردی درباره تناسب بیان میکنیم که در حل مسائل مختلف کاربرد دارند.

جدول تناسب | چگونه جدول تناسب بنویسم با مثال؟
جدولی که نسبتهای برابر را داخل آن قرار میدهند، را جدول تناسب میگویند.
برای فهم بهتر تناسب در ریاضی و نحوه تشکیل جدول تناسب، درادامه به حل چند مثال مختلف میپردازیم.
مثال ۱: تعیین تناسب بین دو نسبت
آیا مقادیر زیر با هم متناسباند؟
الف) ۸ مداد و ۱۲ دفتر – ۱۶ مداد و ۲۴ دفتر
ب) ۷ ماشین و ۹ دوچرخه – ۲۱ ماشین و ۳۰ دوچرخه
الف) ابتدا مقادیر را درون یک جدول تناسب قرار میدهیم و متناسب بودن آنها را بررسی میکنیم.
| ۱۶ | ۸ | تعداد مداد |
| ۲۴ | ۱۲ | تعداد دفتر |
| ۱۶ بهروی ۲۴ | ۸ بهروی ۱۲ | نسبت تعداد مداد به دفتر |
رابطه بالا نشان میدهد که این دو نسبت با هم برابرند. بنابراین، میتوان گفت تعداد مداد با تعداد دفتر متناسب است.
ب) تناسب مقادیر را در یک جدول بررسی میکنیم.
| ۲۱ | ۷ | تعداد ماشین |
| ۳۰ | ۹ | تعداد دوچرخه |
| ۲۱ بهروی ۳۰ | ۷ بهروی ۹ | نسبت تعداد ماشین به دوچرخه |
عدد ۷ در ۳ ضرب شده و حاصل آن ۲۱ شده است. پس باید ۹ را هم در ۳ ضرب کنیم تا دو نسبت مساوی باشند، اما همانطور که میبینید، حاصل ۹ در ۳ برابر با ۲۷ میشود که با مقدار دادهشده در صورت مسئله یعنی ۳۰ متفاوت است. بنابراین، این دو نسبت با هم متناسب نیستند.
مثال ۲: محاسبه نسبت در جدول تناسب
یک قناد برای پخت یک نوع شیرینی، از شکر و آرد با نسبت ۲ به ۳ استفاده میکند. اگر آرد بهکاررفته برای پخت این نوع شیرینی ۱۸۰۰ گرم باشد، مقدار شکر موردنیاز چقدر خواهد بود؟

جواب: ابتدا یک جدول تناسب بهشکل زیر تشکیل میدهیم.
| ؟ | ۲ | مقدار شکر |
| ۱۸۰۰ | ۳ | مقدار آرد |
حالا باید مشخص کنیم چه عددی در ۳ ضرب شده که حاصل آن برابر با ۱۸۰۰ است. برای این کار، ۱۸۰۰ را تقسیم بر ۳ میکنیم.
برای اینکه دو نسبت با هم تناسب داشته باشند، عدد بهدست آمده یعنی ۶۰۰ را در ۲ هم ضرب میکنیم.
| ۱۲۰۰ | ۶۰۰ × ۲ | مقدار شکر |
| ۱۸۰۰ | ۶۰۰ × ۳ | مقدار آرد |
بنابراین، مقدار شکر موردنیاز برای پخت شیرینی ۱۲۰۰ گرم است. توجه داشته باشید که چون مقدار آرد برحسب گرم است، مقدار شکر هم برحسب گرم بهدست میآید.
پیشنهاد مطالعه: انجام راحت محاسبات با جمع و تفریق فرایندی
مثال ۳: تعیین مقدار مجهول در جدول تناسب
مقادیر مجهول در جدول تناسب زیر را بهدست آورید.
| ؟ | ۹ |
| ۵۶۰ | ؟ |
| ۳۲۰ | ۴۰ |
جواب: این جدول سه نسبت مساوی را نشان میدهد. برای اینکه رابطه بین نسبتها را بهدست آوریم، از نسبت معلوم یعنی نسبت ۴۰ به ۳۲۰ استفاده میکنیم. بنابراین ابتدا باید رابطه بین ۴۰ و ۳۲۰ را مشخص کنیم؛ یعنی ببینیم ۴۰ در چه عددی ضرب شده که مقدار آن ۳۲۰ شده است.
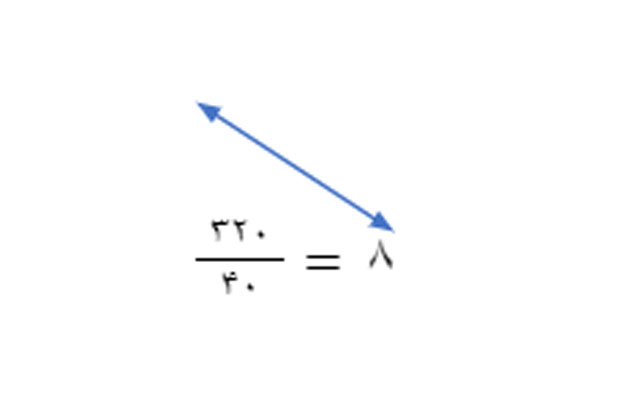
پس، عددی که در ۴۰ ضرب شده، ۸ است. این عدد را برای نسبت اول و دوم هم بهکار میبریم.
| ۷۲ | ۸ × ۹ |
| ۸ ÷ ۵۶۰ | ۷۰ |
| ۳۲۰ | ۸ × ۴۰ |
پیشنهاد مطالعه: تبدیل کسر به اعشار – تبدیل کسر به عدد مخلوط
مثال ۴: طرفین وسطین در جدول تناسب
مقدار خواستهشده در جدول زیر را تعیین کنید.
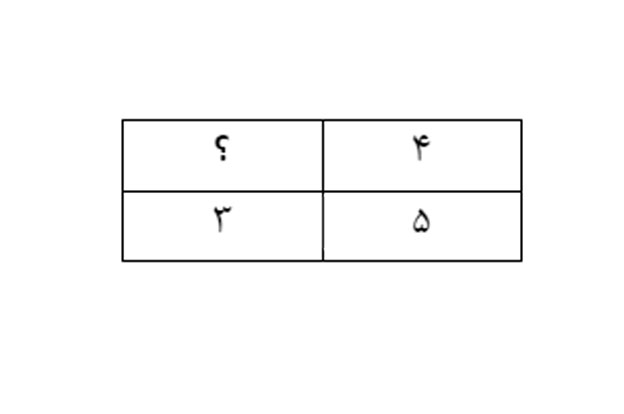
جواب: در این مسئله نمیتوان رابطهای بین نسبتها پیدا کرد. بههمین دلیل، برای تعیین مقدار نامعلوم از روش طرفین وسطین یا روش پروانهای که قبلاً آن را آموزش دادیم، استفاده میکنیم.
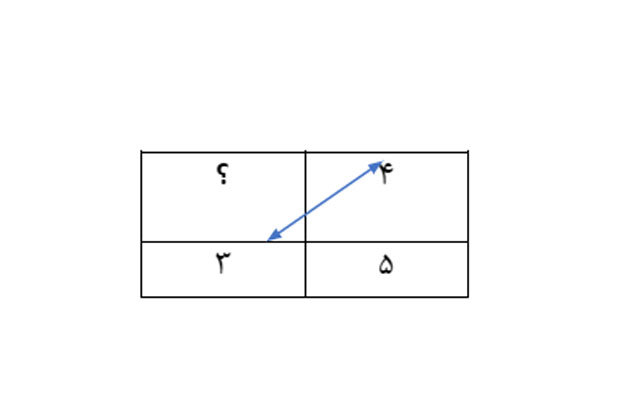
۵ × ? = ۴ × ۳
۵ × ? = ۱۲
برای اینکه مشخص کنیم چه عددی در ۵ ضرب شده که حاصل آن ۱۲ شده است، باید ۱۲ را بر ۵ تقسیم کنیم:
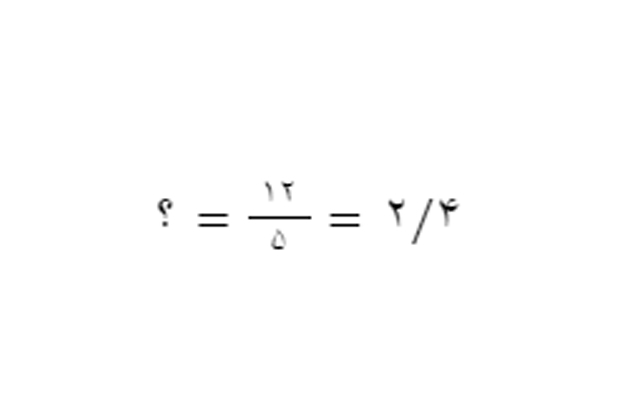
پیشنهاد مطالعه: میانگین چیست؟
مثال ۵: تناسب در محاسبات مالی
علی و خواهرش با کمک هم ۵ میلیون تومان پول پسانداز کردهاند. اگر نسبت پولی که علی پسانداز کرده به پول خواهرش ۴ به ۶ باشد، پسانداز هر کدام از آنها چقدر است؟

جواب: با کمک جدول تناسب، مسئله را حل میکنیم.
| ؟ | ۴ | پسانداز علی |
| ؟ | ۶ | پسانداز خواهرش |
| ۵۰۰۰۰۰۰ | ۱۰ | مجموع پسانداز آنها |
عدد ۱۰ را از جمع نسبتهای پول علی و خواهرش بهدست آوردیم (۱۰ =۶ + ۴ ). حالا بهراحتی میتوانیم مقدار پول پسانداز هر یک را محاسبه کنیم.
| ۲۰۰۰۰۰۰ | ۵۰۰۰۰۰ × ۴ | پسانداز علی |
| ۳۰۰۰۰۰۰ | ۵۰۰۰۰۰ × ۶ | پسانداز خواهرش |
| ۵۰۰۰۰۰۰ | ۵۰۰۰۰۰ × ۱۰ | مجموع پسانداز آنها |
بنابراین، مقدار پسانداز علی ۲ میلیون تومان و مقدار پسانداز خواهرش ۳ میلیون تومان است.
پیشنهاد مطالعه: نحوه محاسبه درصد
تفاوت بین نسبت و تناسب
همانطور که گفتیم، تناسب، تساوی بین دو یا چند نسبت را نشان میدهد. بهطور کلی، نسبت و تناسب دو مفهوم نزدیک به هم محسوب میشوند که تفاوتهایی نیز با هم دارند. در جدول زیر، فرق این دو را بررسی میکنیم:
| نسبت | تناسب |
| برای مقایسه اندازه دو چیز با واحد یکسان استفاده میشود. | برای بیان رابطه دو نسبت استفاده میشود. |
| با علامت “:” یا خط کسری نمایش داده میشود. | با علامت “::” یا “=” نشان داده میشود. |
| یک عبارت است. | یک معادله است. |
تناسب با شکل
به شکل زیر دقت کنید. میخواهیم نسبت قسمت رنگشده آبی به کل شکل را بنویسیم. همانطور که میبینیم این شکل به سه قسمت مساوی تقسیم شده و از این سه بخش دوتای آنها رنگ شده است. بنابراین، نسبت ۲ به ۳ است و میتوانیم آن را بهشکل کسری ۲/۳ بنویسیم.

سخن پایانی
تناسب در ریاضی را برای نسبتهای مساوی بهکار میبرند. اگر دو نسبت برابر باشند، میگوییم با هم تناسب دارند یا متناسباند. تناسب بین نسبتها را در جدولی بهنام جدول تناسب نشان میدهند. زمانی که در نسبتهای برابر یک یا چند مقدار نامعلوم داشته باشیم، این جدول برای درک مسئله بسیار کمککننده خواهد بود.
سؤالات متداول
- تناسب در ریاضی یعنی چه؟
تناسب در ریاضی را برای نسبتهای مساوی بهکار میبرندِ. برای مثال، اگر دو نسبت برابر باشند، میگوییم با هم تناسب دارند. - چه نسبتهایی را متناسب میگویند؟
نسبتهایی که با هم برابرند را متناسب میگویند. - جدول تناسب چیست؟
جدولی است که تناسب بین نسبتها را نشان میدهد و برای تعیین مقادیر نامعلوم در نسبتهای برابر بسیار کاربرد دارد.