فهرست مطالب
Toggleمحاسبه محیط متوازی الاضلاع ازجمله مباحث اولیه محیط و مساحت اشکال هندسی است که دانشآموزان در مقطع ابتدایی برای اولین بار با آن آشنا میشوند. بنابراین، خوب است که بهجای حفظ کردن فرمول برای محاسبه محیط این شکل هندسی، ابتدا آن را بهصورت مفهومی بیاموزند تا هم بتوانند مسائل ریاضی را حل کنند و هم آن را در زندگی روزمره بهکار ببرند.
ما در این مقاله قصد داریم ابتدا دانشآموزان عزیز را با مفهوم محیط متوازی الاضلاع آشنا کنیم، سپس همراه با معرفی فرمول محیط متوازی الاضلاع مثالهای متنوعی را حل کنیم تا نحوه محاسبه محیط متوازی الاضلاع کلاس سوم را برای اولین بار، بهتر و سادهتر یاد بگیرند. البته، در کنار خواندن این مقاله، پیشنهاد میکنیم مقاله محیط چیست را نیز مطالعه کنید تا با مفهوم محیط بیشتر آشنا شوید.
متوازی الاضلاع چیست؟
متوازیالاضلاع یک چهارضلعی است که هر دو ضلع روبهرویی آن با هم مساوی و موازی هستند.
انواع متوازیالاضلاع عبارتند از: مربع، مستطیل و لوزی.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
محیط متوازی الاضلاع چیست؟
دور تا دور یک متوازی الاضلاع (هر چهار ضلع متوازی الاضلاع) را با یک تکه نخ بهشکل زیر بپوشانید و زمانی که نخ کل اضلاع را پوشش داد آن را قیچی کنید. حالا اندازه طول نخ را با خطکش اندازه بگیرید. اندازه طول نخ همان محیط متوازی الاضلاع است.
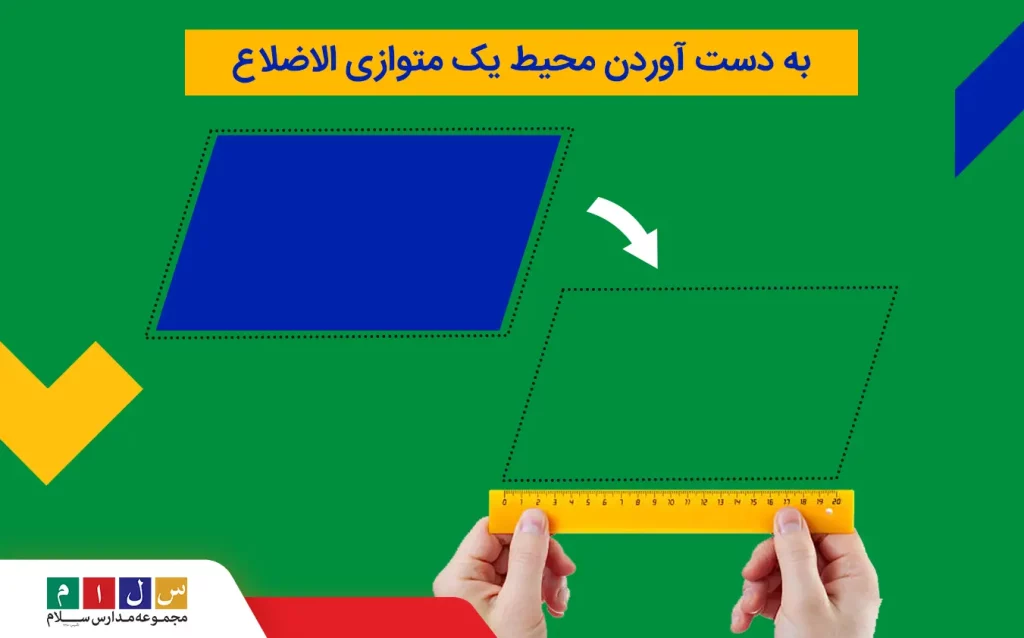
بنابراین، نتیجه میگیریم که محیط متوازی الاضلاع برابر است با اندازه دور تا دور متوازی الاضلاع.
ساده ترین فرمول محیط متوازی الاضلاع
سادهترین روش برای محاسبه محیط متوازی الاضلاع این است که اندازه چهار ضلع آن را با هم جمع کنیم. شکل زیر را در نظر بگیرید:

محیط این متوازی الاضلاع بهصورت زیر محاسبه میشود:
ضلع زرد + ضلع سبز + ضلع آبی + ضلع قرمز = محیط متوازی الاضلاع
در بخش ویژگیهای متوازی الاضلاع گفتیم که طول اضلاع روبهروی متوازی الاضلاع مانند مستطیل با هم برابر است. یعنی
ضلع سبز = ضلع قرمز
ضلع زرد = ضلع آبی
پس فرمول محیط متوازی الاضلاع را میتوان بهصورت زیر نوشت:
(ضلع آبی + ضلع قرمز) × ۲ = ضلع آبی × ۲ + ضلع قرمز × ۲ = محیط متوازی الاضلاع
این فرمول، محاسبه محیط متوازی الاضلاع را برای ما راحتتر میکند چون دیگر لازم نیست تکتک اضلاع را با هم جمع کنیم. فقط کافیست اندازه ضلع بزرگ و کوچک (دو ضلع مجاور) متوازی الاضلاع را داشته باشیم و آن را در فرمول بالا جایگذاری کنیم. در ادامه چند مثال حل میکنیم تا بهتر متوجه شوید.
مثال ۱: محیط متوازی الاضلاع زیر را محاسبه کنید.

در این متوازی الاضلاع، فقط اندازه ضلع بزرگ و کوچک یعنی دو ضلع مجاور داده شده است. میدانیم که اضلاع روبهروی متوازی الاضلاع با هم برابر است، یعنی در این شکل، دو ضلع بهاندازه ۳ سانتیمتر و دوضلع بهاندازه ۵ سانتیمتر داریم.
در اینجا میتوان محیط متوازی الاضلاع را به دو روش محاسبه کرد:
روش اول: اینکه تکتک اضلاع را بهصورت زیر با هم جمع کنیم:
۵ سانتیمتر + ۵ سانتیمتر + ۳ سانتیمتر + ۳ سانتیمتر = محیط متوازی الاضلاع
۱۶ سانتیمتر = ۱۰ سانتیمتر + ۶ سانتیمتر =محیط متوازی الاضلاع
روش دوم: از فرمول جمع دو ضلع مجاور × ۲ = محیط متوازی الاضلاع استفاده کنیم:
جمع دو ضلع مجاور × ۲ = محیط متوازی الاضلاع
(۵ سانتیمتر + ۳ سانتیمتر) × ۲ =محیط متوازی الاضلاع
۱۶ سانتیمتر = (۸ سانتیمتر) × ۲ =محیط متوازی الاضلاع
همانطور که میبینید جواب هر دو روش یکسان بهدست آمد.
نکته: واحد اندازه گیری محیط را با واحد اندازهگیری طول نشان میدهند یعنی میلیمتر، سانتیمتر، متر، کیلومتر و… . مثلاً در مسئله بالا واحد اندازهگیری طول اضلاع، سانتیمتر بود و بههمین دلیل، محیط را هم با واحد اندازهگیری سانتیمتر بهدست آوردیم؛ چون گفتیم که محیط با جمع اندازه طول اضلاع بهدست میآید.
مثال ۲: یک دانشآموز میخواهد محیط پاککنش که بهشکل متوازی الاضلاع است را بهدست آورد. اگر او قاعده متوازی الاضلاع را ۳ سانتیمتر و ضلع مجاور آن را ۲ سانتیمتر اندازه بگیرد، محیط پاککن چند سانتیمتر خواهد بود؟

طبق صورت سؤال، قاعده که در اینجا ضلع بزرگتر است، ۳ سانتیمتر و ضلع دیگر ۲ سانتیمتر است. این اعداد را در فرمول جایگذاری میکنیم:
جمع دو ضلع مجاور × ۲ = محیط پاککن
(۲ سانتیمتر + ۳ سانتیمتر) × ۲ =محیط پاککن
۱۰ سانتیمتر = (۵ سانتیمتر) × ۲ =محیط پاککن
پس محیط پاککن این دانشآموز ۱۰ سانتیمتر است.
مثال ۳: دوندهای قرار است یک زمین بازی بهشکل متوازی الاضلاع را که طول اضلاع مجاور آن ۷۰ متر و ۵۰ متر است دور بزند، اما بعد از اینکه ۲/۳ مسیر را طی میکند خسته میشود و از حرکت میایستد. این دونده چند متر از مسیر را دویده است؟
در صورت سؤال گفته شده که دونده قرار است زمین بازی را دور بزند یعنی دور تا دور متوازی الاضلاع را بدود. پس باید محیط این زمین بازی را بهدست آوریم:

جمع دو ضلع مجاور × ۲ = محیط زمین بازی
(۵۰ متر + ۷۰ متر) × ۲ =محیط زمین بازی
۲۴۰ متر = (۱۲۰ متر) × ۲ =محیط زمین بازی
پس محیط این زمین بازی ۲۴۰ متر بوده است؛ اما چون دونده فقط ۲۳ مسیر (محیط) را دویده است، باید ۲۳ را در ۲۴۰ متر ضرب کنیم تا ببینیم دونده چند متر دویده است.
محیط متوازی الاضلاع × ۲۳ = مسیری که دونده دویده است
۱۶۰ متر = ۴۸۰۳ = ۲۴۰ متر × ۲۳ =مسیری که دونده دویده است
بنابراین، دونده ۱۶۰ متر از مسیر را دویده است.
مثال ۴: پدر علی میخواهد دور تا دور حوض حیاطشان که بهشکل متوازی الاضلاع است را با کاشیهای کوچک زیبا کند. اگر طول اضلاع حوض ۲ متر و یک متر باشد، این حوض به چند متر کاشی نیاز دارد؟
پدر علی میخواهد دور تا دور حوض یعنی محیط حوض را کاشیکاری کند. پس برای اینکه بدانیم چند متر کاشی لازم است، باید محیط حوض را بهدست آوریم:
جمع دو ضلع مجاور × ۲ = محیط حوض
(۱ متر + ۲ متر) × ۲ =محیط حوض
۶ متر = (۳ متر) × ۲ =محیط حوض
پس برای زیبا کردن این حوض، ۶ متر کاشی لازم است.
مثال ۵: دو باغچه بهشکل زیر داریم. میخواهیم دور تا دور آنها را گل بکاریم. در باغچه بزرگتر چند متر بیشتر از باغچه کوچکتر باید گل کاشت؟

اول باید بدانیم در هر باغچه چند متر میتوان گل کاشت. یعنی ابتدا باید محیط باغچهها را بهدست آوریم.
جمع دو ضلع مجاور × ۲ = محیط باغچه بزرگتر
(۳ متر + ۴ متر) × ۲ =محیط باغچه بزرگتر
۱۴ متر = (۷ متر) × ۲ =محیط باغچه بزرگتر
جمع دو ضلع مجاور × ۲ = محیط باغچه کوچکتر
(۲ متر + ۳ متر) × ۲ = محیط باغچه کوچکتر
۱۰ متر = (۵ متر) × ۲ = محیط باغچه کوچکتر
برای اینکه بدانیم در باغچه بزرگتر باید چند متر بیشتر گل کاشت، محیط دو باغچه را از هم کم میکنیم:
۴ متر = ۱۰ متر – ۱۴ متر = محیط باغچه کوچکتر – محیط باغچه بزرگتر
پس در باغچه بزرگتر باید ۴ متر بیشتر گل بکاریم.
سایر فرمول ها برای محاسبه محیط متوازی الاضلاع
با توجه به اطلاعات مسئله، همیشه نمیتوان برای محاسبه محیط متوازی الاضلاع از فرمول ساده آن استفاده کرد؛ چون ممکن است اندازه یک ضلع را به ما ندهند. در این مواقع، باید از فرمولهای دیگری استفاده کرد که در ادامه، آنها را با مثال توضیح خواهیم داد.
توجه: فرمولهایی که در ادامه بیان میشوند، برای دانشآموزان متوسطه اول و دوم که در این مقاطع با محیط متوازی الاضلاع به صورت جبری و با مثلثات آشنا میشوند، میتواند کاربردی باشد.
فرمول محیط متوازی الاضلاع با قطرها و یک ضلع
اگر اندازه طول قطرها و یکی ازضلعهای متوازی الاضلاع مشخص باشد، از فرمول زیر محیط متوازی الاضلاع را بهدست میآوریم:
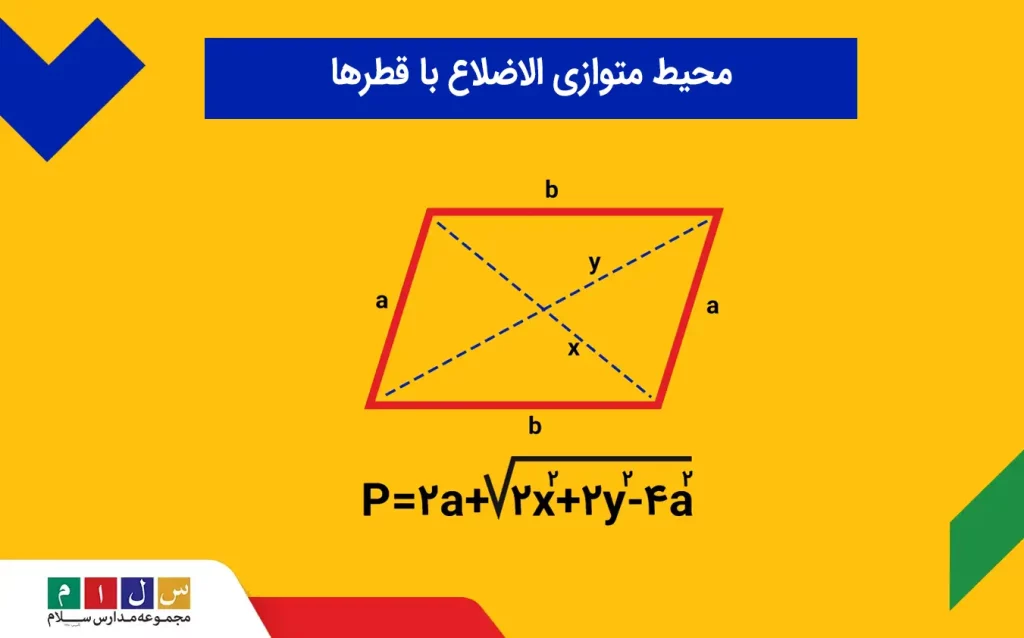
- x و y: قطرها
- a: طول یکی از اضلاع
- p:محیط
مثال: محیط متوازی الاضلاع زیر را بهدست آورید.
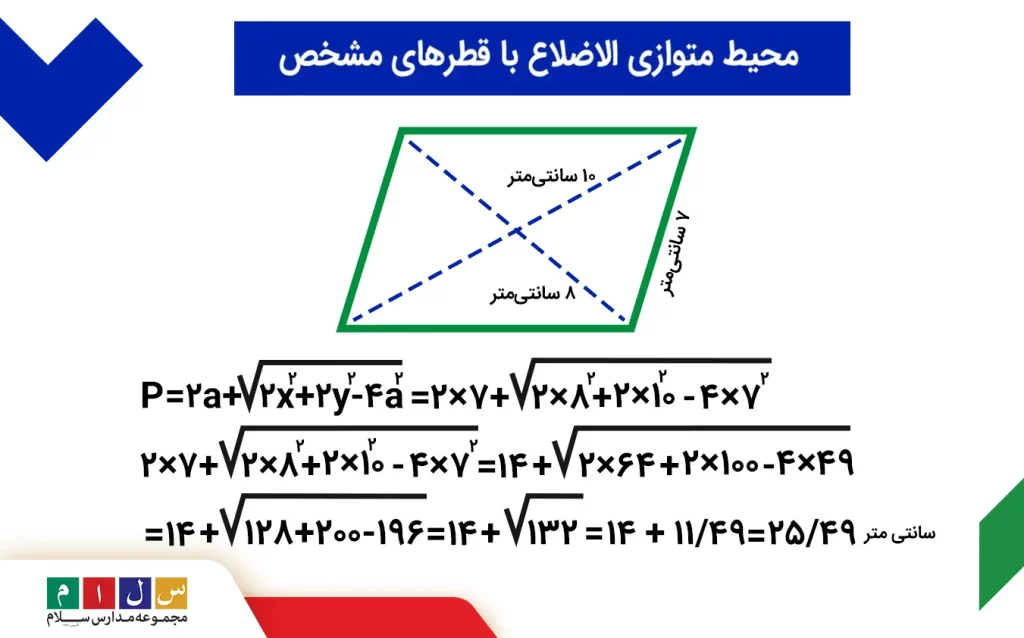
در این شکل اندازه قطرها و یکی از اضلاع را داریم؛ پس، از فرمول P=2a+√2x²+2y²-4a²محیط را محاسبه میکنیم:
- X (قطر اول): 8 cm
- Y (قطر دوم): 10 cm
- ۷cm:a
P=۲a + √۲x² + ۲y²-۴a²= ۲x۷ + √۲ x ۸² + ۲ x ۱۰² – ۴x۷²
P= ۲ x ۷ + √۲ x ۸²+ ۲ x ۱۰² – ۴x۷² = ۱۴ + √۲ x ۶۴+ ۲ x۱۰۰ – ۴ x ۴۹
p = ۱۴+ √۱۲۸ + ۲۰۰ – ۱۹۶= ۱۴ + √۱۳۲= ۱۴ + ۱۱.۴۹= ۲۵.۴۹cm
فرمول محیط متوازی الاضلاع با قاعده و ارتفاع
اگر اندازه قاعده، ارتفاع و یکی از زاویهها مشخص باشد، فرمول محیط متوازی الاضلاع بهشکل زیر خواهد بود:
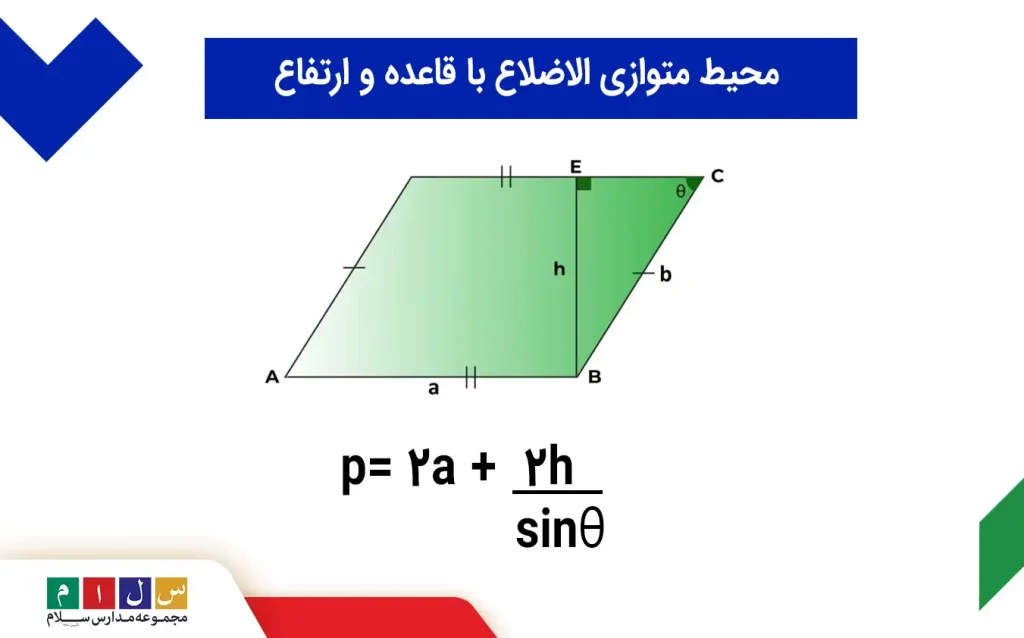
- a: طول قاعده
- h: ارتفاع
- θ: زاویه داخلی
مثال: محیط شکل زیر را محاسبه کنید.θ: زاویه داخلی
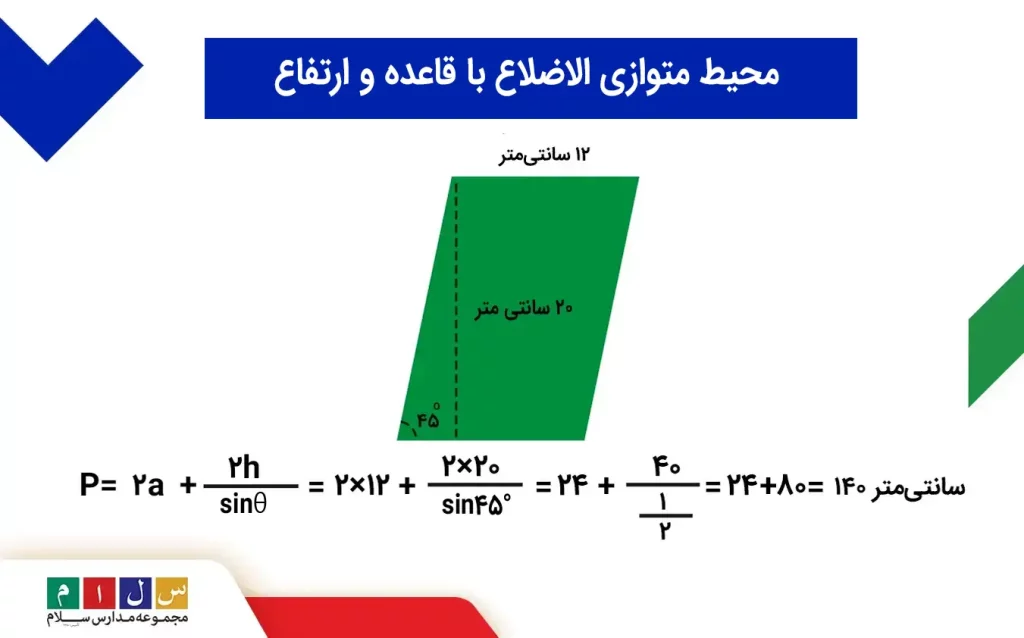
در شکل بالا، قاعده، ارتفاع و زاویه داخلی متوازی الاضلاع داده شده است؛ بنابراین، کافیست مقادیر آنها را در فرمول p=۲a + (۲h ÷ sinθ) جایگذاری کنیم:
- a: ۱۲ cm
- h: ۲۰ cm
- °θ:۴۵
p= ۲a + (۲h ÷ sinθ)= ۲ x + (۲ x۲۰) ÷ sin۴۵° = ۲۴ + (۴۰ ÷ (۱÷۲)) = ۲۴ + ۸۰ =۱۰۴ cm
فرمول های محیط متوازی الاضلاع:
| فرمول محیط با دو ضلع | P=۲a+b | 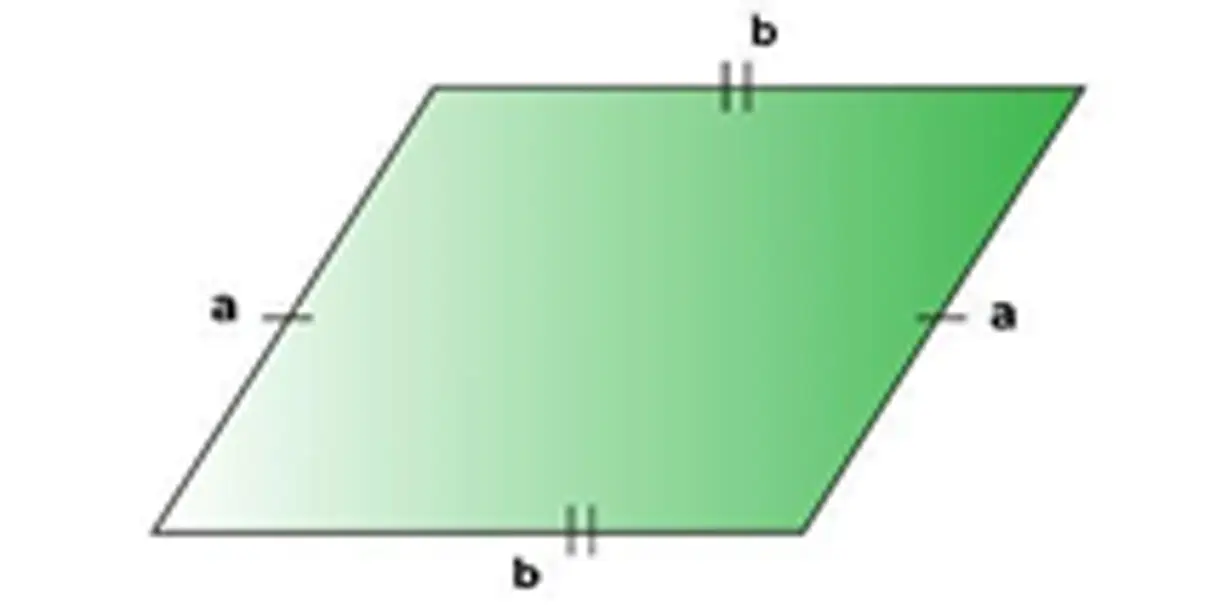 |
| فرمول محیط با قطرها و یک ضلع | P= ۲a + √۲x² + ۲y² – ۴a² | 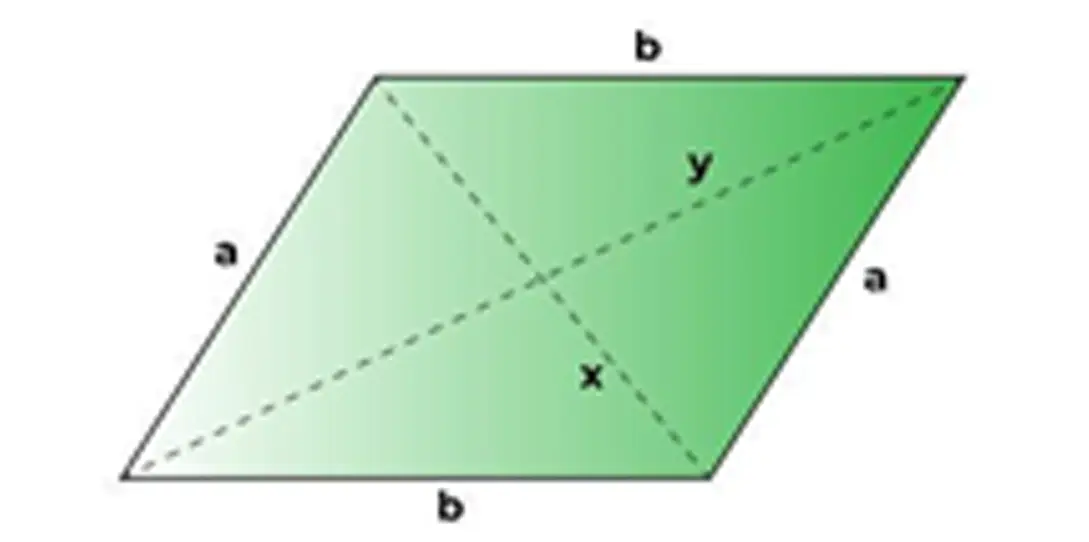 |
| فرمول محیط با قاعده و ارتفاع | p= ۲a + (۲h ÷ sinθ) | 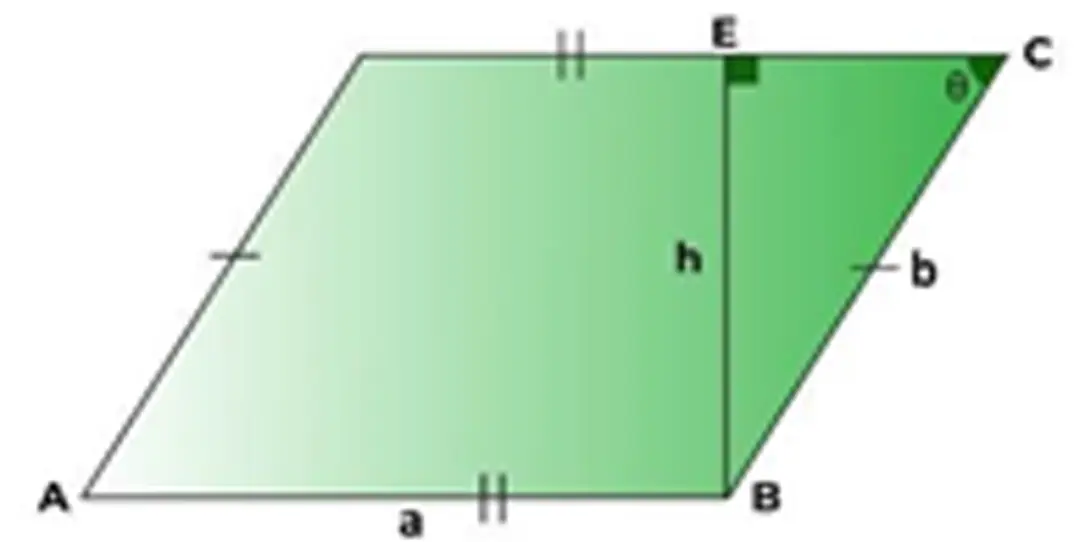 |
محاسبه آنلاین محیط متوازی الاضلاع
امروزه ابزارهای آنلاین زیادی برای انجام محاسبات هندسی وجود دارد. یکی از ابزارهای رایج برای محاسبه محیط متوازیالاضلاع موتور جستجوی گوگل است. با یک جستجوی ساده عبارت «parallelogram perimeter» در گوگل، کادری نمایش داده میشود که کافی است طول دو ضلع متوازی الاضلاع را در آن وارد کنید تا محیط متوازی الاضلاع بهدست آید.
کار کردن با ابزار محاسبه گوگل ساده است، اما فقط بر اساس ضلعها جواب میدهد و امکان محاسبه محیط با قطر یا ارتفاع را ندارد. اگر بخواهید محیط را با کمک قطر یا ارتفاع حساب کنید، سایت Omni Calculator گزینهی کاملتری برای شما خواهد بود.
اشتراک متوازی الاضلاع با سایر اشکال هندسی
بسیاری از اشکال هندسی در واقع حالتهای خاصی از متوازیالاضلاع هستند.
- متوازیالاضلاعی که همه زاویههای آن قائمه باشند، مستطیل است.
- متوازیالاضلاعی که هر چهار ضلع آن با هم برابر باشند لوزی است.
- متوازیالاضلاعی که همه زاویههای آن قائمه و همه اضلاع آن برابر باشند مربع است.
شباهت و تفاوت متوازیالاضلاع با مستطیل
در هر دو شکل:
- شباهت= اضلاع روبهرو با هم مساوی و موازیاند و قطرها یکدیگر را نصف میکنند.
- تفاوت= در مستطیل قطرها مساوی هستند اما در متوازیالاضلاع لزوماً برابر نیستند.
شباهت و تفاوت متوازیالاضلاع با لوزی
- شباهت= در هر دو شکل زاویههای تند و باز دیده میشود.
- تفاوت= قطرها همدیگر را نصف میکنند، اما لزوماً با هم مساوی نیستند.
سخن پایانی
محاسبه محیط متوازی الاضلاع کار چندان سختی نیست؛ فقط کافیست محیط را مفهومی یاد بگیرید و ویژگیهای متوازی الاضلاع را بدانید. سادهترین فرمول متوازی الاضلاع، جمع اضلاع آن یا بهعبارتی دو ضربدر جمع دو ضلع مجاور آن است. البته با استفاده از قطرها و قاعده و ارتفاع نیز میتوان محیط این چهارضلعی را بهدست آورد؛ اما از آنها زمانی استفاده میشود که تنها اندازه یکی از اضلاع را داشته باشیم.
سوالات متداول
- محیط متوازی الاضلاع چیست؟
محیط متوازی الاضلاع، اندازه دور تا دور آن است که از جمع چهار ضلع آن بهدست میآید - فرمول ساده محیط متوازی الاضلاع کلاس چهارم چیست؟
جمع دو ضلع مجاور × ۲ - آیا فرمول دیگری برای محاسبه متوازی الاضلاع وجود دارد؟
بله. با استفاده از قطرها، قاعده و ارتفاع هم میتوان محیط این شکل هندسی را محاسبه کرد.









