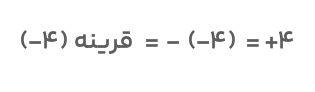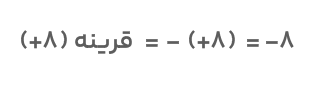قرینه عدد چیست ؟ | آموزش قرینه اعداد به زبان ساده + مثال

واژه «قرینه» در زبان فارسی، به معنای تناظر و همانندی است. این کلمه در ریاضی و هندسه معنای خاص خود را دارد و اگر به‌‌خوبی درک شود به شما کمک می‌‌کند تا مفاهیمی همچون تقارن را در محورهای مختصات و اشکال هندسی بهتر یاد بگیرید. قرینه اعداد یکی از مباحث مهم در ریاضی است.

اگر دانش‌‌آموز کلاس هفتم هستید و می‌‌خواهید قرینه اعداد را سریع و آسان بیاموزید، جای درستی آمده‌‌اید چرا که این آموزش مخصوص شماست. در این درس‌‌نامه برایتان توضیح می‌‌دهیم که قرینه عدد چیست و قرینه یک عدد نسبت به عدد دیگر چگونه به دست می‌‌آید.

همچنین به حل مثال‌‌هایی می‌‌پردازیم که مفهوم قرینه عدد در ذهن شما تثبیت شود.

قرینه عدد چیست ؟

در آموزش قرینه شکل به‌‌طور کامل توضیح دادیم که اگر یک شکل را نسبت به یک نقطه یا خط بازتاب دهیم، شکلی مشابه شکل اولیه ایجاد می‌‌شود. در این حالت، شکل ثانویه را قرینه شکل اولیه می‌‌نامیم و می‌‌گوییم دو شکل قرینه یکدیگرند. به همین صورت برای اعداد نیز می‌‌توان مفهوم قرینه را به کار برد. البته در عددها شیوه به دست آوردن قرینه اندکی متفاوت است و معمولاً برای درک بهتر آن از محور اعداد استفاده می‌‌شود.

مراحل تعیین قرینه اعداد با استفاده از محور به‌‌صورت زیر است:

• گام اول : ابتدا با کمک خط‌‌کش یک محور مانند شکل زیر رسم می‌‌کنیم. وسط محور را که همان مرکز آن است مشخص کرده و عدد ۰ را پایین آن یادداشت می‌‌کنیم. عدد ۰ در اینجا مانند مرکز تقارن عمل می‌‌کند.

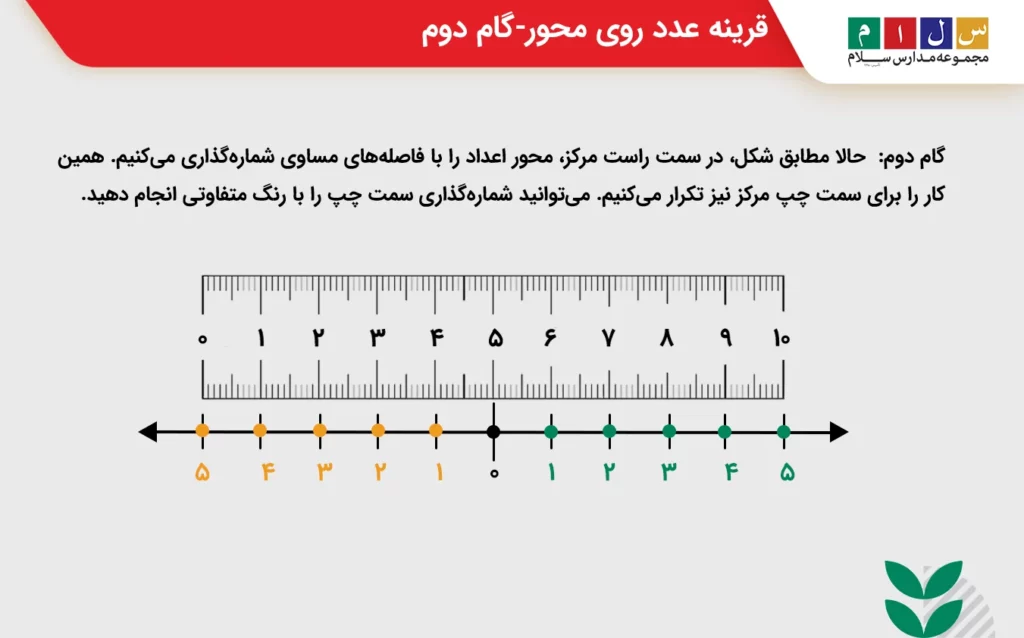
• گام دوم: حالا مطابق شکل، در سمت راست مرکز، محور اعداد را با فاصله‌‌های مساوی شماره‌‌گذاری می‌‌کنیم. همین کار را برای سمت چپ مرکز نیز تکرار می‌‌کنیم. می‌‌توانید شماره‌‌گذاری سمت چپ را با رنگ متفاوتی انجام دهید.

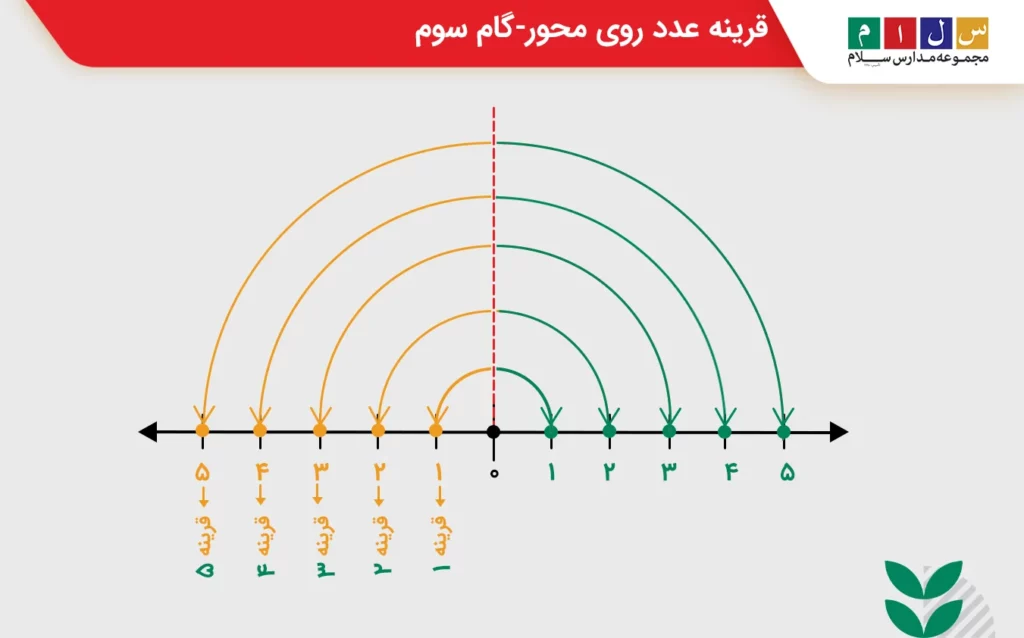
• گام سوم: اگر عدد صفر را مانند یک خط تقارن در نظر بگیریم و محور را از این قسمت تا کنیم، خواهیم دید که اعداد سمت راست دقیقاً روی اعداد مشابه‌‌شان در سمت چپ منطبق می‌‌شوند. این موضوع نشان می‌‌دهد که اعداد سمت چپ صفر قرینه اعداد سمت راست آن هستند. برای مثال، عدد ۵ در سمت چپ قرینه عدد ۵ در سمت راست است و بالعکس. همان‌‌طور که می‌‌بینید، عدد ۵ در هر دو سمت محور از مرکز یعنی عدد ۰ فاصله یکسانی دارد.

قرینه اعداد صحیح

اعداد صحیح مجموعه‌‌ای از اعداد کامل شامل اعداد مثبت، منفی و صفر هستند. به اعداد بالای صفر اعداد مثبت و به اعداد پایین صفر اعداد منفی گفته می‌‌شود. اگر بخواهیم اعداد صحیح را روی محور اعداد نمایش دهیم، اعداد مثبت سمت راست محور و اعداد منفی سمت چپ آن قرار می‌‌گیرند.

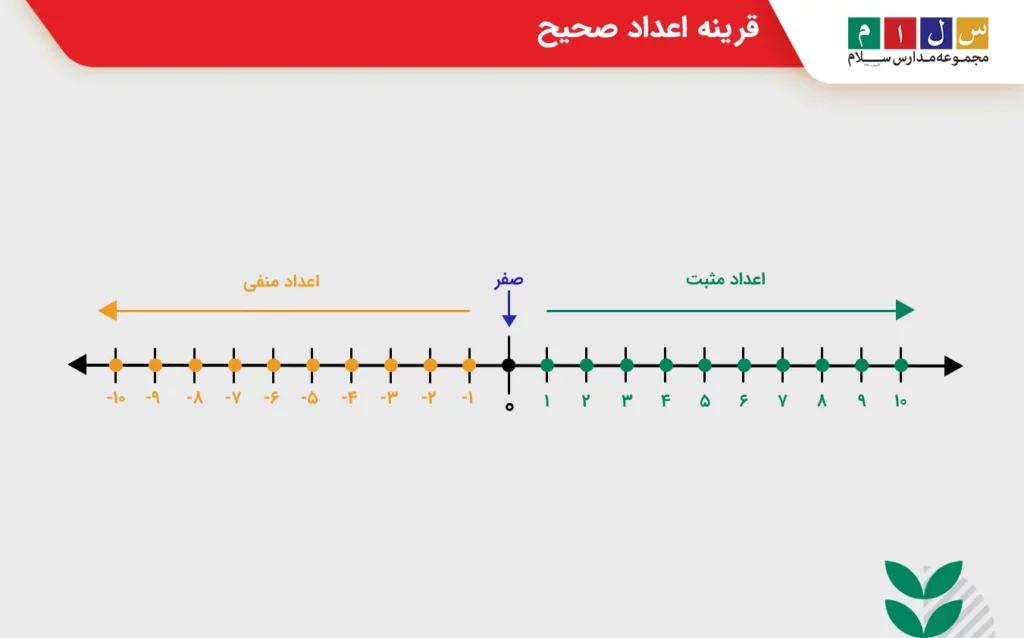
در بخش قرینه عدد چیست بیان کردیم که در محور اعداد، اعداد سمت چپ صفر قرینه اعداد مشابهی هستند که با همان فاصله در سمت راست عدد صفر قرار گرفته‌‌اند. به این ترتیب، می‌‌توان گفت اعداد منفی و اعداد مثبت قرینه یکدیگرند.

نکته: عدد صفر نه مثبت است نه منفی و قرینه آن خود صفر است.

با توجه به اینکه اعداد مثبت و منفی قرینه هم هستند، می‌‌توانیم نتیجه بگیریم که قرینه هر عددی، برابر با منفی آن عدد است. به بیان دیگر، اگر یک عدد را در -۱ یا علامت (-) ضرب کنیم، قرینه آن به دست خواهد آمد. پس با توجه به محور اعداد در تصویر بالا می‌‌توانیم بنویسیم:

• ۱+ قرینه ۱- است، درنتیجه قرینه ۱- برابر با ۱+ است.
• ۲+ قرینه ۲- است، درنتیجه قرینه ۲ – برابر با ۲+ است.
• ۳+ قرینه ۳- است، درنتیجه قرینه ۳- برابر با ۳+ است.
• ۴+ قرینه ۴- است، درنتیجه قرینه ۴ – برابر با ۴+ است.
• ۵+ قرینه ۵- است، درنتیجه قرینه ۵- برابر با ۵+ است.
•۶+ قرینه ۶-است، درنتیجه قرینه ۶ – برابر با ۶+ است.

از جمله‌‌های بالا می‌‌توان فهمید که اگر قرینه یک عدد را قرینه کنیم، با خود آن عدد برابر خواهد بود. بنابراین، می‌‌توانیم بگوییم قرینه قرینه هر عدد با خود آن عدد برابر است.
به‌‌عنوان مثال، فرض کنید می‌‌خواهیم قرینه قرینه عدد ۲۵- را به دست آوریم. برای یافتن جواب ابتدا باید قرینه ۲۵- را تعیین کنیم. می‌‌دانیم که قرینه هر عددی با ضرب آن عدد در ۱- به دست می‌‌آید. پس خواهیم داشت:

(-۱) × (-۲۵) = +۲۵

حالا ۲۵+ را با همین روش قرینه می‌‌کنیم تا قرینه قرینه ۲۵- مشخص شود. داریم:

(-۱) × (+۲۵)= -۲۵

همان‌‌طور که می‌‌بینید، قرینه قرینه ۲۵- برابر با ۲۵- یعنی خود همان عدد شد.

مثال اول: قرینه عدد منفی ۴ چه عددی است ؟

اکنون که می‌‌دانیم قرینه عدد چیست می‌‌توانیم به‌‌راحتی قرینه هر عددی را به دست آوریم. ۴- یک عدد صحیح منفی است. اگر بخواهیم این عدد را قرینه کنیم کافی‌‌ست آن را در علامت (-) یا عدد (۱-) ضرب کنیم. بنابراین، قرینه این عدد برابر است با

این دقیقاْ همان جوابی است که در جملات بالا به آن اشاره کردیم.

مثال دوم: قرینه عدد ۸ چه عددی است ؟

عدد ۸ یا ۸+ یک عدد مثبت است و برای قرینه کردن تنها لازم است در یک علامت منفی (-) ضرب شود. پس قرینه ۸ را به‌‌صورت زیر به دست می‌‌آوریم:

مثال سوم: قرینه قرینه ۹ چند است ؟

برای تعیین قرینه قرینه عدد ۹ کافی‌‌ست به‌‌ازای هر بار قرینه کردن یک علامت (-) در سمت چپ عدد قرار دهیم یا به‌‌عبارتی، عدد را دو بار در علامت منفی ضرب کنیم. خواهیم داشت:

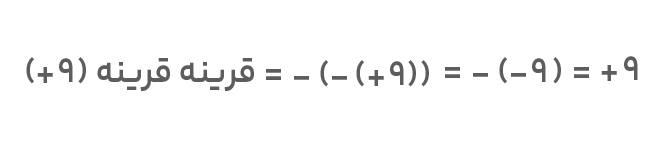
مثال چهارم: قرینه عدد ۵۶ بزرگ تر است یا ۱۲-؟

ابتدا دو عدد را با روشی که توضیح دادیم قرینه می‌‌کنیم:

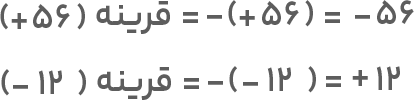
با توجه به اینکه اعداد منفی از اعداد مثبت کوچک‌‌ترند، قرینه عدد ۵۶ که یک عدد منفی است از قرینه عدد ۱۲- که یک عدد مثبت است کوچک‌‌تر خواهد بود.
قرینه کردن تنها مختص اعداد صحیح نیست، هر عدد غیرصحیح ازجمله عدد اعشاری و عدد کسری را نیز می‌‌توان قرینه کرد. مثال‌‌های زیر نمونه‌‌هایی از این دست هستند:

چهار عمل اصلی ریاضی روی عدد و قرینه آن

حالا که با قرینه عدد آشنا شدید، خوب است چهار عمل جمع، تفریق، ضرب و تقسیم روی عدد و قرینه‌‌اش را نیز یاد بگیرید. هر کدام از این عملیات ریاضی نتیجه‌‌ای به دنبال دارند که می‌‌تواند در محاسبات ریاضی به کارتان بیاید. در ادامه، هر یک از این چهار عمل اصلی را با مثال بررسی می‌‌کنیم.

جمع عدد و قرینه آن

اگر یک عدد را با قرینه‌‌اش جمع ببندیم حاصل آن صفر خواهد شد. این رابطه همواره برقرار است. برای مثال، حاصل‌‌جمع عدد ۱۲۸ و قرینه‌‌اش یعنی ۱۲۸ – برابر است با:

۱۲۸ + ( -۱۲۸ ) = ۱۲۸ -۱۲۸ = ۰

تفریق عدد و قرینه آن

تفریق عدد و قرینه عدد ۲ برابر آن عدد است. اگر به یاد داشته باشید در بخش‌‌های قبل گفتیم که فاصله هر عدد تا صفر برابر با فاصله قرینه آن عدد تا صفر است. این موضوع نشان می‌‌دهد که فاصله (یا اختلاف) یک عدد و قرینه‌‌اش ۲ برابر آن عدد است. مثلاً عدد ۱۵ را در نظر بگیرید. قرینه این عدد مساوی ۱۵- و درنتیجه اختلاف آن‌‌ها مساوی است با:

۱۵ – (-۱۵) =۱۵+۱۵ =۲×۱۵ =۳۰

برای اعداد منفی نیز همین‌‌طور است. برای مثال، اختلاف ۳۴- و قرینه آن ۳۴ به‌‌صورت زیر به دست می‌‌آید:

-۳۴ – (+۳۴) = -۳۴ – ۳۴ = ۲× (-۳۴) = -۶۸

این رابطه نشان می‌‌دهد که فاصله ۳۴- و قرینه‌‌اش ۳۴ برابر با ۶۸ واحد است. برای بیان فاصله معمولاً اعداد را به‌‌صورت مثبت می‌‌نویسیم.

ضرب عدد و قرینه آن

حاصل‌‌ضرب یک عدد در قرینه آن مساوی است با منفی توان دو آن عدد. مثال زیر این رابطه را به‌‌خوبی نشان می‌‌دهد.

-۷ × ۷ = -۷^۲ = -۴۹

تقسیم عدد و قرینه آن

تقسیم عدد بر قرینه آن عدد همواره برابر با ۱- است. مثلاً اگر عدد اعشاری ۷۱/۲۳ را بر قرینه‌‌اش تقسیم کنیم، داریم:

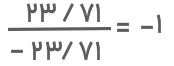
چگونه قرینه عدد نسبت به عدد دیگر را به دست آوریم؟

تا اینجای آموزش، قرینه کردن عدد نسبت به عدد صفر را آموختیم و عدد صفر را به‌‌عنوان مبنای قرینه در نظر گرفتیم. در این بخش، می‌‌خواهیم نحوه قرینه کردن عدد نسبت به عدد دیگر را به شما بیاموزیم. برای قرینه کردن یک عدد نسبت به مبدأ غیرصفر، باید مراحلی را که در ادامه به آن‌‌ها اشاره می‌‌کنیم طی کنید.
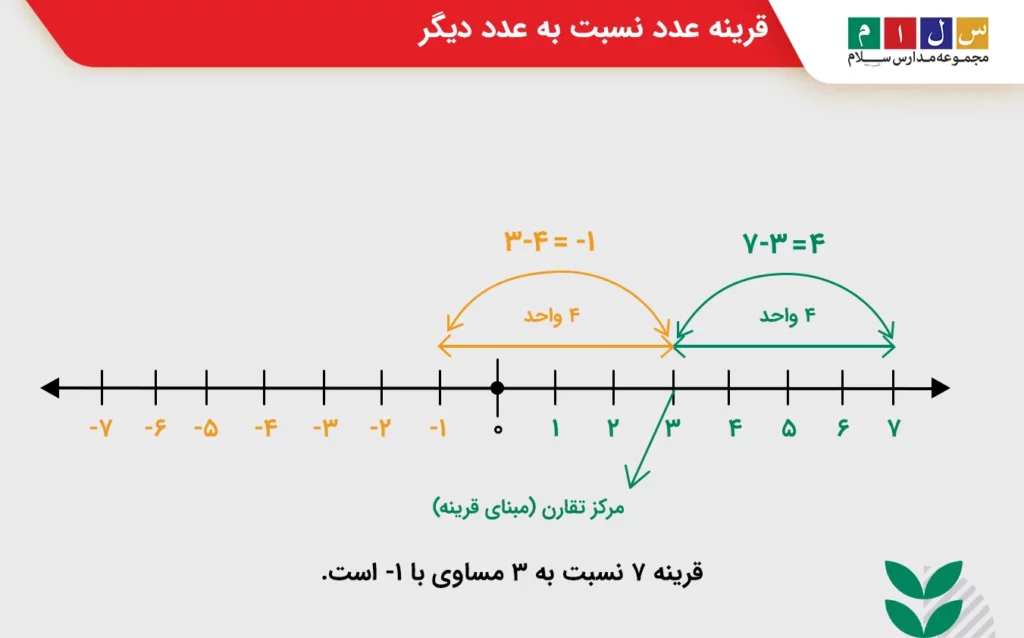
فرض کنید می‌‌خواهیم قرینه عدد ۷ را نسبت به ۳ پیدا کنیم. برای این کار ابتدا یک محور به‌‌شکل زیر رسم می‌‌کنیم. در اینجا چون می‌‌خواهیم قرینه عدد را نسبت به ۳ بیابیم، باید ۳ را به‌‌عنوان مرکز تقارن در نظر بگیریم. به‌‌منظور یافتن قرینه عدد ۷ نخست فاصله مرکز تقارن یعنی ۳ تا عدد ۷ را حساب می‌‌کنیم.

فاصله ۷ تا ۳ تنها ۴ واحد است. برای اینکه قرینه عدد ۷ را نسبت به ۳ تعیین کنیم کافی‌‌ست از سمت چپ ۳ نیزبه‌‌همان اندازه یعنی ۴ واحد جلو برویم. به هر عددی که رسیدیم آن عدد قرینه ۷ نسبت به ۳ خواهد بود. همان‌‌طور که در شکل زیر مشاهده می‌‌کنید، این عدد ۱- است. پس قرینه ۷ نسبت به ۳ مساوی است با ۱-.

گاهی اوقات لازم است قرینه یک عدد بزرگ را به دست آوریم. در چنین مواقعی دیگر نمی‌‌توانیم از محور اعداد استفاده کنیم و باید روشی را به کار ببریم که بدون رسم محور ما را به جواب نهایی برساند. در ادامه به حل چند مثال دراین‌‌باره می‌‌پردازیم.

مثال اول: قرینه عدد ۷ نسبت به عدد ۱

در این مثال، قرینه عدد ۷ نسبت به ۱ خواسته شده است. پس باید عدد ۱ را مبنای قرینه یا همان مرکز تقارن قرار دهیم. حالا فاصله عدد ۷ و ۱ را محاسبه می‌‌کنیم:

۷-۱=۶

فاصله عدد ۷ و ۱ برابر با ۶ واحد است. بنابراین، جهت تعیین قرینه بایستی از عدد ۱ شروع کرده و به‌‌اندازه ۶ واحد به‌‌سمت اعداد کوچک‌‌تر از ۱ برویم. با توجه به اینکه هرچه جلوتر می‌‌رویم اعداد کوچک‌‌تر می‌‌شوند، باید ۶ واحد از ۱ کم کنیم تا عدد حاصل که همان قرینه ۷ نسبت به عدد ۱ است به دست آید. خواهیم داشت:

۱-۶ = – ۵

قرینه عدد ۷ نسبت به عدد ۱ برابر با ۵- است.

مثال دوم: قرینه عدد ۶ نسبت به عدد ۲

در اینجا مبنای قرینه، عدد ۲ است. ابتدا باید ببینیم فاصله عدد ۶ از ۲ چقدر است. برای این کار باید آن‌‌ها را از هم کم کنیم:

۶-۲=۴

فاصله موردنظر ۴ واحد است. پس باید از عدد ۲ شروع کرده و ۴ واحد به‌‌سمت اعداد کوچک‌‌تر از ۲ حرکت کنیم. این یعنی اینکه برای مشخص کردن قرینه باید ۴ واحد را از ۲ کم کنیم:

۲-۴ = -۲

پس قرینه ۶ نسبت به ۲ مساوی است با ۲-.

مثال سوم: قرینه عدد ۵ نسبت به ۹

مرکز تقارن در این مثال ۹ است که باید قرینه ۵ نسبت به آن را به دست آوریم. ازآنجا که عدد ۵ کوچک‌‌تر از ۹ است و ۴ واحد از آن فاصله دارد، برای تعیین قرینه باید ۴ واحد به مرکز تقارن یعنی ۹ اضافه شود. در این صورت، قرینه ۵ نسبت به ۹ برابر با مقدار زیر خواهد بود:

۹+۴=۱۳

مثال چهارم: قرینه عدد ۴ نسبت به عدد ۱

مانند مثال‌‌های قبل ابتدا سراغ تعیین مرکز تقارن می‌‌رویم. مرکز تقارن ۱ است و به‌‌اندازه ۳ واحد از عدد ۴ که باید قرینه آن را مشخص کنیم فاصله دارد. مرکز تقارن (۱) از ۴ کوچک‌‌تر است. پس قرینه ۴ نسبت به ۱ عددی کوچک‌‌تر از ۱ خواهد بود و برای به دست آوردن آن بایستی به‌‌همان اندازه یعنی ۳ واحد از ۱ کم کنیم:

۱ -۳ = -۲

فرمول قرینه عدد نسبت به عدد دیگر

عدد اصلی – (مرکز تقارن × ۲) = قرینه عدد نسبت به عدد دیگر

در این رابطه عدد اصلی همان عددی است که باید قرینه آن را تعیین کنیم. اگر مثال سوم بخش قبل را با این فرمول حل کنیم خواهیم داشت:

(۲×۹) – ۵ = ۱۸ – ۵ =۱۳

می‌‌بینید که پاسخ همان شد که در بخش قبل به دست آوردیم. شما نیز می‌‌توانید برای بررسی صحت جواب‌‌های به‌‌دست‌‌آمده در بخش قبل از این فرمول استفاده کنید. در اینجا یک مثال دیگر نیز حل می‌‌کنیم تا بهتر متوجه شوید.

مثال: قرینه عدد ۶- نسبت به ۳ چند است؟

پاسخ: عدد اصلی در این سؤال۶- و مرکز تقارن یا مبنای قرینه عدد ۳ است. با جای‌‌گذاری این اعداد در فرمول بالا می‌‌توانیم قرینه را حساب کنیم. داریم:

قرینه عدد در دستگاه مختصات

دستگاه مختصات شامل دو محور عمود بر هم است که صفحه را به چهار ناحیه مجزا تقسیم می‌‌کنند. در این دستگاه هر نقطه دارای طول و عرض معینی است. فرض کنید نقطه‌‌ای مانند (آ) داریم که طول آن ۲ و عرض آن ۳ است. مختصات این نقطه را به‌‌صورت زیر نشان می‌‌دهیم:

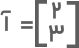
عدد بالا طول و عدد پایین عرض نقطه است. اگر بخواهیم قرینه این نقطه را نسبت به محور عمودی و افقی و نسبت به مبدأ مختصات تعیین کنیم باید به‌‌صورت زیر عمل کنیم:
• قرینه نقطه آ نسبت به مبدأ مختصات: برای به دست آوردن قرینه این نقطه نسبت به مبدأ مختصات هم طول و هم عرض را قرینه می‌‌کنیم:

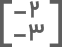
• قرینه نقطه آ نسبت به محور افقی (محور xها): برای قرینه کردن هر نقطه نسبت به محور افقی تنها کافی‌‌ست مقدار عرض را قرینه کنیم:

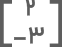
• قرینه نقطه آ نسبت به محور عمودی (محور yها): قرینه نقطه آ نسبت به محور عمودی از قرینه کردن طول آن به دست می‌‌آید:

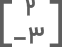
در شکل زیر مکان نقاط قرینه (آ) برای هر سه حالت نشان داده شده است.

سخن پایانی

در این مقاله خواندید که قرینه عدد چیست و چگونه به دست می‌‌آید. قرینه هر عدد را با گذاشتن علامت منفی در سمت چپ آن نمایش می‌‌دهند. به‌‌طور کلی، قرینه هر عدد منفی عددی مثبت و قرینه هر عدد مثبت عددی منفی خواهد بود. کاربرد قرینه عدد در تقارن و تعیین مختصات نشان می‌‌دهد که یادگیری این مفهوم چقدر در درک سایر مفاهیم ریاضی و هندسی ضروری است. ازهمین‌‌رو، ما در این مطلب سعی کردیم مفهوم قرینه عدد را به‌‌گونه‌‌ای توضیح دهیم که راه برای شما هموارتر شود و بتوانید درک درستی از این مبحث داشته باشید.

سؤالات متداول

1. قرینه صفر چیست؟
   قرینه صفر همان عدد صفر است.
2. مجموع یک عدد و قرینه آن برابر با چه عددی است؟
   حاصل‌‌جمع یک عدد و قرینه آن برابر با صفر است.
3. حاصل تفریق عدد و قرینه عدد چیست؟
   اختلاف عدد و قرینه عدد دو برابر آن عدد است.
4. قرینه قرینه هر عدد با خود عدد برابر است درست یا نادرست ؟
   قرینه قرینه هر عددی برابر با خود آن عدد است. بنابراین، این جمله به‌‌درستی بیان شده است.
5. قرینه ۵ نسبت به کدام عدد برابر منفی یک است ؟
   با توجه به اینکه یک عدد و قرینه آن هر کدام فاصله یکسانی از مبنای قرینه (مرکز تقارن) دارند، برای به دست آوردن مرکز تقارن کافی‌‌ست عدد و قرینه آن را از یکدیگر کم کنیم تا فاصله آن‌‌ها تعیین شود. سپس، فاصله به‌‌دست‌‌آمده را بر ۲ تقسیم می‌‌کنیم تا مرکز تقارن به دست آید:
   
   

مرکز تقارن ۳ است. بنابراین، قرینه ۵ نسبت به عدد ۳ برابر منفی۱ است.