مساحت جانبی چیست؟ ׀ فرمول مساحت جانبی حجم های هندسی + حل مثال

مفهوم مساحت جانبی برای آن دسته از حجم‌‌های هندسی تعریف می‌‌شود که سطح جانبی دارند. منظور از مساحت جانبی همان اندازه سطح جانبی است. سطح جانبی به وجه یا وجه‌‌های کناری یک شکل سه‌‌بعدی گفته می‌‌شود که بین دو قاعده و در برخی شکل‌‌ها بین رأس و قاعده آن شکل قرار می‌‌گیرند.

در این آموزش از مجموعه آموزش‌‌های ریاضی قصد داریم فرمول مساحت جانبی در اشکال گوناگون را ارائه کرده و با حل مثال‌‌های کاربردی شما را با نحوه محاسبه آن آشنا کنیم. پس با ما همراه باشید.

مساحت جانبی استوانه

استوانه از سه وجه شامل دو وجه دایره‌‌ای و یک وجه مستطیل‌‌شکل ساخته شده است. دو وجه دایره‌‌ای، قاعده و وجه مستطیلی، وجه جانبی یا سطح جانبی نام دارد. بنابراین، سطح جانبی در یک استوانه یک سطح به‌‌شکل مستطیل است که بین دو قاعده دایره‌‌ای قرار می‌‌گیرد. شکل زیر به‌‌خوبی سطح جانبی در یک استوانه را نشان می‌‌دهد.

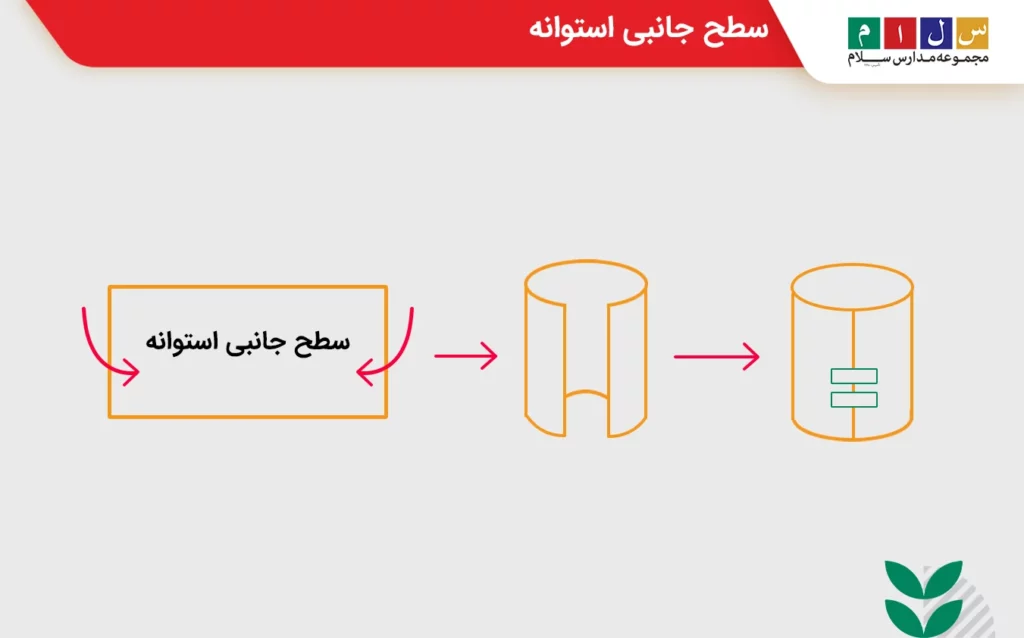
با توجه به اینکه طول سطح جانبی مستطیلی همان محیط قاعده دایره‌‌ای و عرض آن ارتفاع استوانه است، می‌‌توانیم یک فرمول کلی برای مساحت جانبی استوانه به دست آوریم و آن را به‌‌صورت زیر بنویسیم:

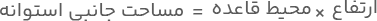
قاعده یک دایره است. بنابراین، محیط آن را از فرمول محیط دایره می‌‌توان حساب کرد:

با قرار دادن این فرمول در رابطه بالا خواهیم داشت:

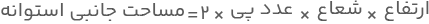
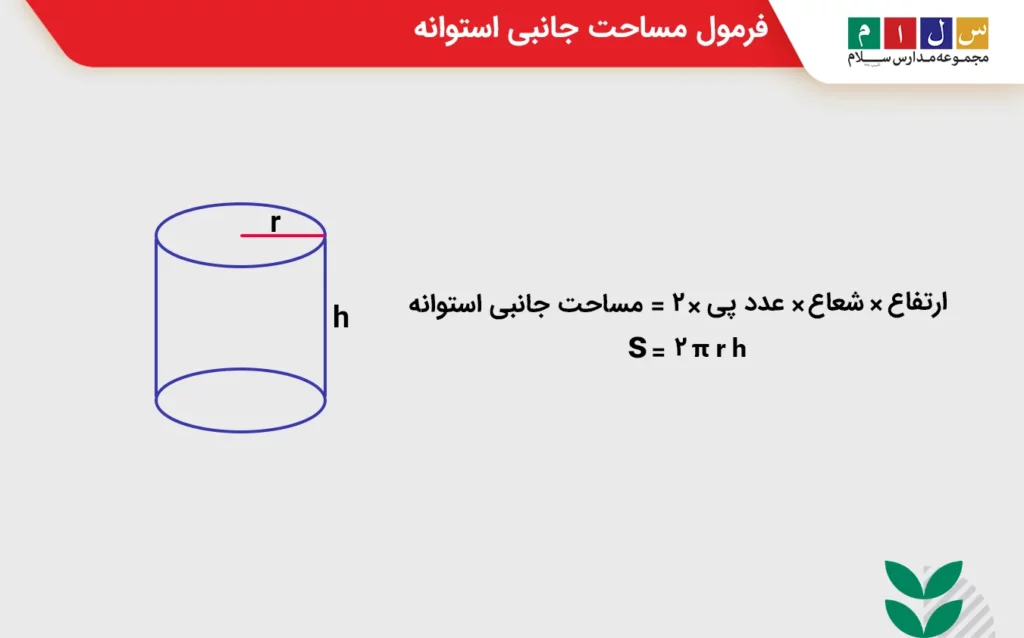
به‌‌طور کلی، اگر ارتفاع استوانه را h و شعاع قاعده را r در نظر بگیریم، فرمول جبری مساحت جانبی استوانه به‌‌شکل زیر خواهد بود:

S=۲πrh

S‌ مساحت جانبی استوانه و π عدد پی است.

در اینجا خوب است نکته‌‌ای را به شما یادآوری کنیم. گاهی اوقات برخی از دانش‌‌آموزان به‌‌جای مساحت جانبی استوانه از عبارت مساحت جانبی دایره استفاده می‌‌کنند که کاملاً اشتباه است. دایره یک شکل مسطح و دوبعدی است و نمی‌‌توان سطج جانبی و درنتیجه مساحت جانبی برای آن تعریف کرد. بنابراین، دقت داشته باشید که همواره عبارت درست را به کار ببرید.

مثال: استوانه‌‌ای داریم که شعاع آن ۱۲ سانتی‌‌متر و ارتفاعش ۳۵ سانتی‌‌متر است. مساحت جانبی این استوانه را بیابید.
پاسخ: اطلاعات داده‌‌شده در این مسئله به‌‌شرح زیر است:

• r (شعاع قاعده): ۱۲
• h (ارتفاع استوانه): ۳۵

اکنون کافی‌‌ست این مقادیر را در فرمول مساحت جانبی استوانه جای‌‌گذاری کنیم. داریم:

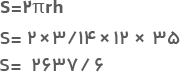
به‌‌این‌‌ترتیب، مساحت جانبی برابر با ۲۶۳۷/۶ سانتی‌‌متر مربع است.

مساحت جانبی منشور

منشور یک چندوجهی است که از دو وجه مشابه و موازی به‌‌نام قاعده و تعدادی وجه جانبی به‌‌شکل مربع، مستطیل و یا متوازی‌الاضلاع ساخته شده است. قاعده‌‌های یک منشور چندضلعی هستند و به همین دلیل، در منشور تعداد وجه‌‌های جانبی به تعداد اضلاع قاعده‌‌های آن بستگی خواهد داشت زیرا تعداد وجه‌‌های جانبی به‌‌اندازه تعداد اضلاع تشکیل‌‌دهنده قاعده‌‌هاست.

در ادامه، به نحوه محاسبه مساحت جانبی در انواع منشور خواهیم پرداخت.

مساحت جانبی منشور سه پهلو

منشوری که قاعده آن مثلثی‌‌شکل باشد یا به‌‌عبارتی، از سه ضلع تشکیل شده باشد، منشور سه‌‌پهلو نامیده می‌‌شود زیرا در چنین منشوری تعداد وجه‌‌های جانبی یا پهلوها سه‌‌تا خواهد بود. پهلوها یا وجه‌‌های جانبی وجه‌‌هایی هستند که به قاعده‌‌ها متصل‌‌اند. در شکل زیر وجه‌‌های جانبی یک منشور سه‌‌پهلو نشان داده شده است.

همان‌‌طور که می‌‌بینید، این منشور دارای سه وجه مستطیلی است که هرسه آن‌‌ها سطح جانبی منشور را شکل می‌‌دهند. بنابراین، با توجه به شکل اگر بخواهیم مساحت سطح جانبی منشور را محاسبه کنیم، باید محیط قاعده مثلثی را که همان طول مستطیل است در ارتفاع منشور یعنی عرض مستطیل ضرب کنیم. به‌‌این‌‌ترتیب، فرمول محاسبه مساحت جانبی منشور رابطه‌‌ای به‌‌شکل زیر خواهد بود:

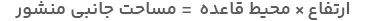
به‌‌عنوان مثال، برای محاسبه مساحت جانبی شکل بالا به‌‌صورت زیر عمل می‌‌کنیم:

۱۲= ۵+۳+۴ = محیط قاعده

درنتیجه

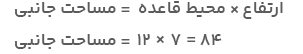
مساحت جانبی منشور چهار پهلو

حالا که دیگر می‌‌دانیم منظور از پهلو چیست، سراغ منشور چهارپهلو می‌‌رویم. منشور چهارپهلو همان‌‌گونه که از نامش پیداست، منشوری با چهار وجه جانبی یا به‌‌عبارتی، منشوری با قاعده‌‌هایی به‌‌شکل چهارضلعی است. در اینجا نیز فرمول مساحت جانبی منشور همان رابطه‌‌ای است که در بخش قبل بیان کردیم یعنی حاصل‌‌ضرب محیط قاعده در ارتفاع منشور. به مثال‌‌هایی که در ادامه حل می‌‌کنیم توجه کنید تا با شیوه محاسبه مساحت جانبی انواع منشور چهارپهلو آشنا شوید.

محاسبه مساحت جانبی مکعب

مکعب یک شش‌‌وجهی است که تمام وجه‌‌های آن مربع‌‌هایی مشابه هستند. شکل ظاهری مکعب شبیه به یک منشور است؛ منشوری که دو قاعده آن و تمام پهلوهایش مربع‌‌شکل‌‌اند. در تصویر زیر می‌‌توانید گسترده یک مکعب را مشاهده کنید.

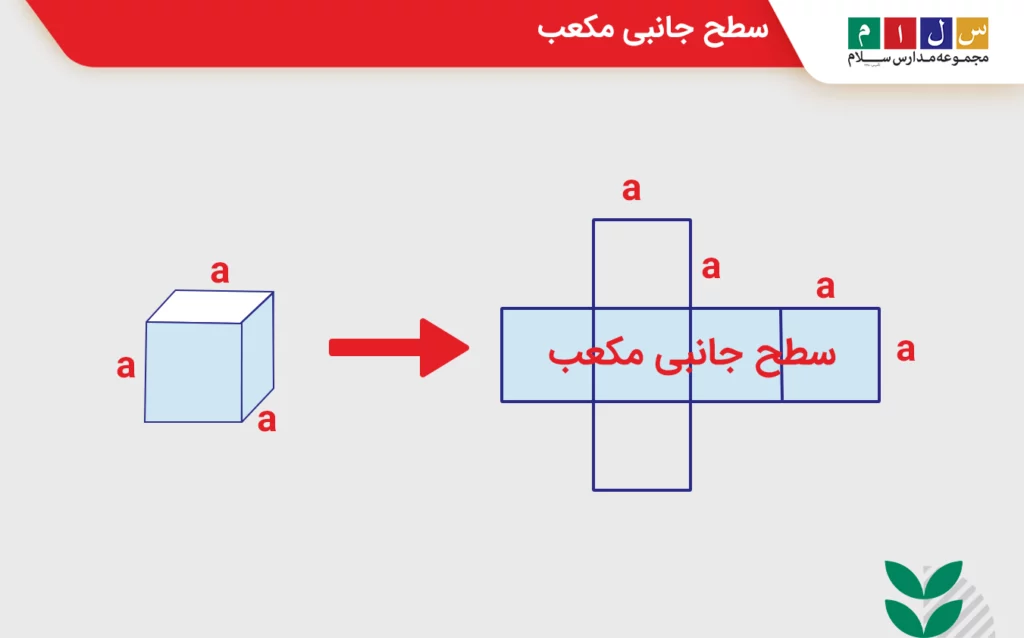
ازآنجا که سطح جانبی یک مکعب شامل چهار مربع یکسان است، فرمول مساحت جانبی مکعب برابر خواهد بود با:

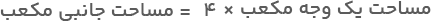
مساحت هر وجه مکعب از توان دوی اندازه ضلع مکعب به دست می‌‌آید. پس فرمول بالا را می‌‌توان به‌‌شکل زیر هم نوشت:

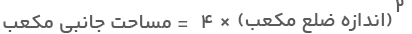
اگر مساحت جانبی مکعب را با S و اندازه ضلع آن را با a نشان دهیم، شکل جبری این فرمول به‌‌صورت زیر خواهد بود:

S=۴a^۲

مثال: اندازه ضلع یک مکعب ۷ سانتی‌‌متر است. سطح جانبی آن را محاسبه کنید.
جواب: با توجه به رابطه‌‌ای که معرفی کردیم، تعیین مساحت جانبی این مکعب بسیار راحت است. تنها کافی‌‌ست اندازه ضلع را در فرمول قرار دهیم:

S=۴a^۲

S=۴(۷)^۲=۴×۴۹=۱۹۶

پس مساحت جانبی مکعب ۱۹۶ سانتی‌‌متر مربع است.

محاسبه مساحت جانبی مکعب مستطیل

مکعب مستطیل نیز یک منشور چهارپهلو است که قاعده‌‌های آن مستطیل هستند. شکل زیر گسترده یک مکعب مستطیل و سطح جانبی آن را نشان می‌‌دهد.

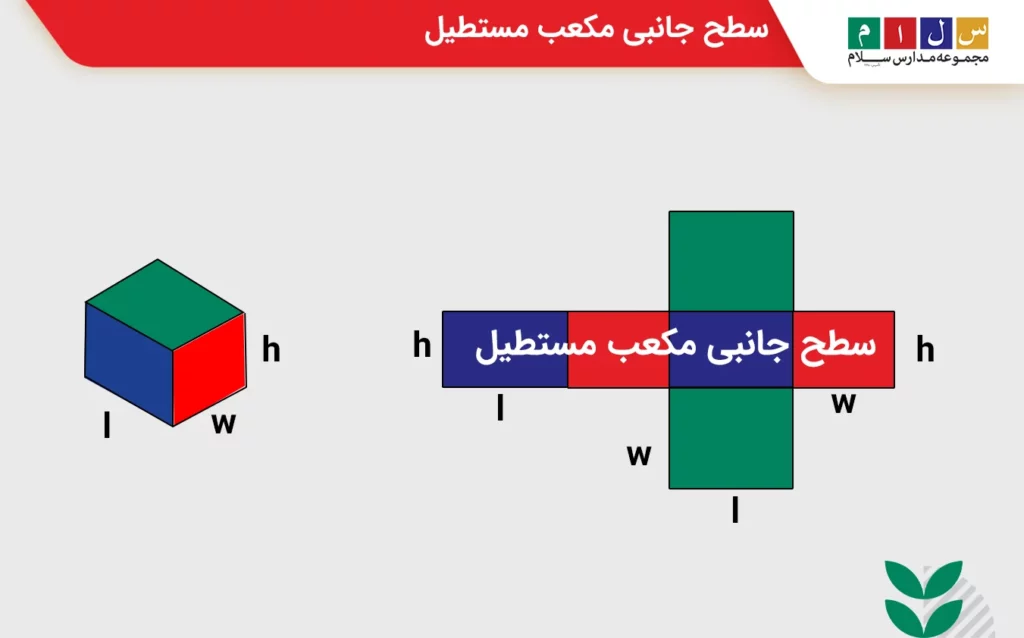
طبق تصویر بالا سطح جانبی مکعب مستطیل از چهار وجه ساخته شده است که دوبه‌‌دو هم‌‌اندازه یکدیگرند. وجه‌‌های هم‌‌اندازه با رنگ مشابه نشان داده شده‌‌اند. ازاین‌‌رو، فرمول محیط قاعده را می‌‌توانیم به‌‌صورت زیر بنویسیم:

P = ۲ × (l+w)

• l: طول مکعب مستطیل
• w: عرض مکعب مستطیل

اگر ارتفاع مکعب را با h نشان دهیم، فرمول کلی مساحت جانبی مکعب مستطیل به‌‌صورت زیر خواهد بود:

S=۲(l+w)h

مثال: مساحت جانبی شکل زیر را به دست آورید.

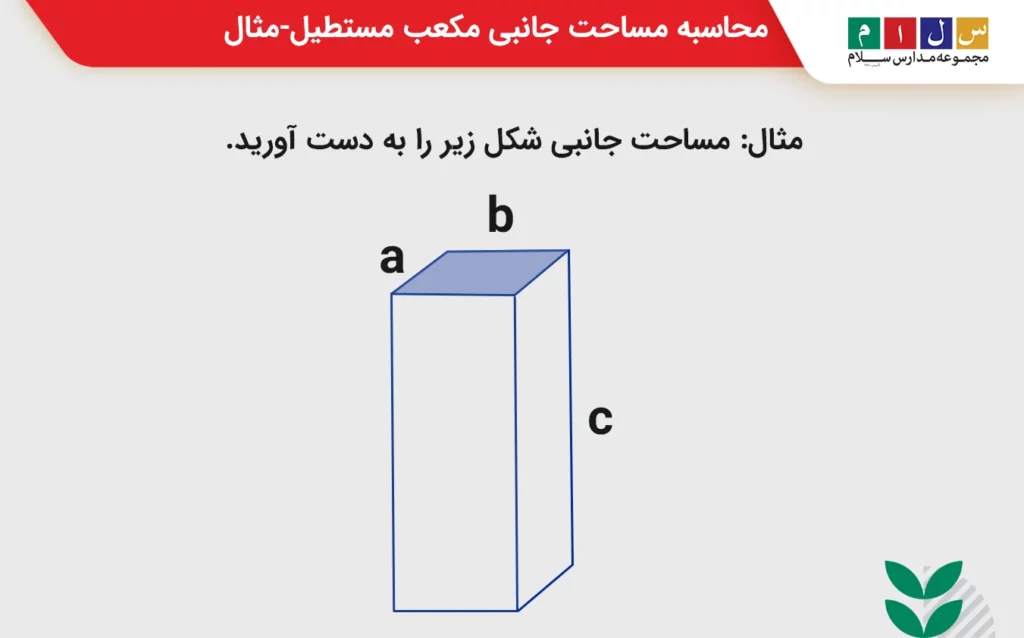
پاسخ: در شکل داده‌‌شده اندازه طول, عرض و ارتفاع مکعب مستطیل برابر است با:
• a: طول مکعب مستطیل
• b: عرض مکعب مستطیل
• c: ارتفاع مکعب مستطیل
به‌‌این‌‌ترتیب، مساحت جانبی با قرار دادن این مقادیر در فرمول بالا به دست خواهد آمد. داریم:

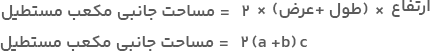
مساحت جانبی منشور ذوزنقه

منشور ذوزنقه منشوری است که قاعده‌‌های آن به‌‌شکل ذوزنقه هستند. در ادامه، مثالی از مساحت جانبی ذوزنقه هفتم حل می‌‌کنیم.
مثال: مساحت جانبی منشور زیر را حساب کنید.

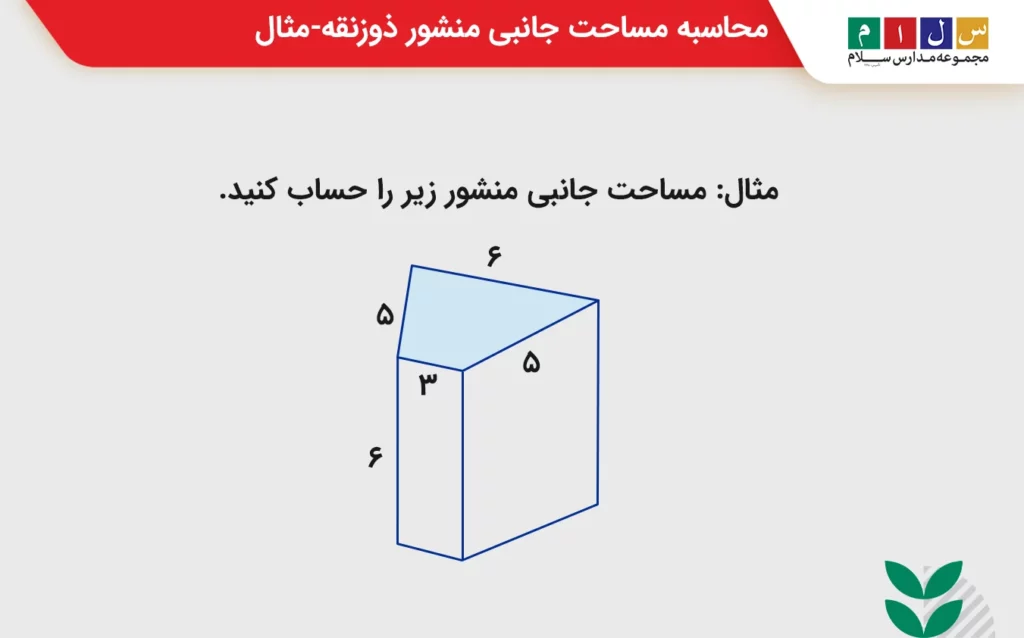
پاسخ: با توجه به اینکه مساحت جانبی انواع منشور از حاصل‌‌ضرب محیط قاعده در ارتفاع آن به دست می‌‌آید، به‌‌راحتی می‌‌توان مساحت جانبی را محاسبه کرد:

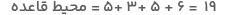
ارتفاع منشور برابر با ۶ است، پس مساحت جانبی مساوی است با:

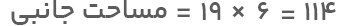
محاسبه مساحت جانبی منشور لوزی

منشور زیر را در نظر بگیرید. قاعده‌‌های این منشور به‌‌شکل لوزی است. لوزی یک چهارضلعی است که هر چهار ضلع آن هم‌‌اندازه هستند. پس می‌‌توان نتیجه گرفت در منشوری که قاعده‌‌های آن لوزی‌‌شکل هستند، چهار وجه جانبی با هم برابرند. محیط قاعده و مساحت جانبی چنین منشوری از روابط زیر تعیین می‌‌شود:

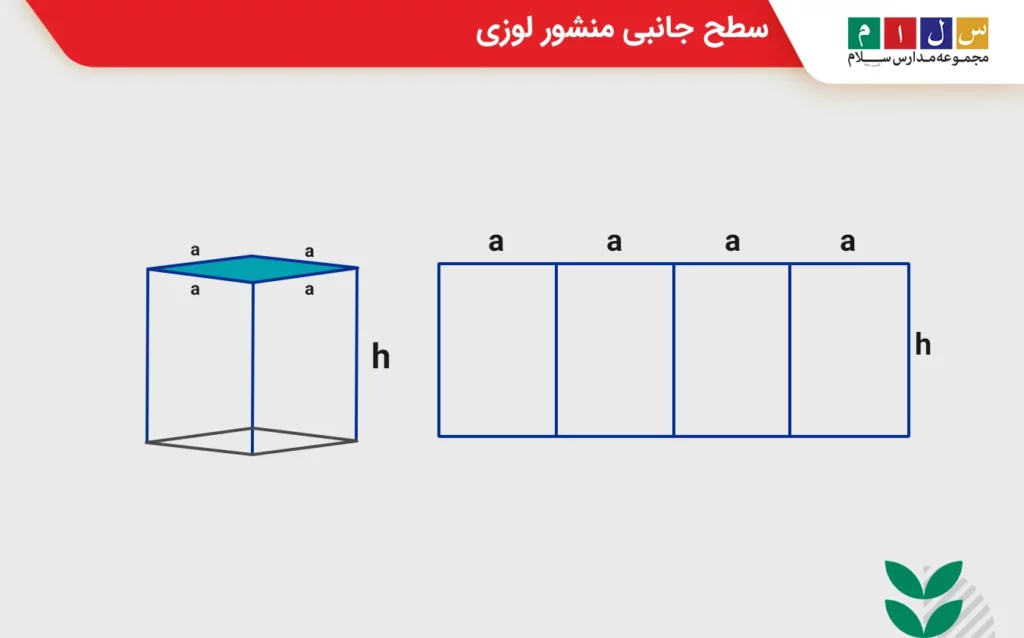
اگر اندازه یک ضلع لوزی را a و ارتفاع منشور را h در نظر بگیریم، فرمول مساحت جانبی را می‌‌توانیم به‌‌صورت جبری بنویسیم:

S=۴ah

مثال: ارتفاع یک منشور لوزی ۱۵ سانتی‌‌متر و اندازه یک ضلع قاعده آن ۲۰ سانتی‌‌متر است. مساحت جانبی این منشور چقدر خواهد بود؟
پاسخ: از فرمول بالا استفاده می‌‌کنیم. با جای‌‌گذاری مقادیر معلوم خواهیم داشت:

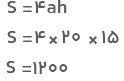
مساحت جانبی منشور ۱۲۰۰ سانتی‌‌متر مربع است.

مساحت جانبی منشور پنج پهلو

منشور پنج‌‌پهلو دارای پنج وجه جانبی است و مانند سایر منشورهایی که تا اینجا درباره آن‌‌ها صحبت کردیم، مساحت جانبی آن محاسبه می‌‌شود. در حالت خاص، اگر قاعده منشور که یک پنج‌‌ضلعی است دارای اضلاع برابری باشد یا به‌‌عبارتی، قاعده یک پنج‌‌ضلعی منتظم باشد، آنگاه هر پنج وجه جانبی با هم برابرند و در این صورت محیط قاعده و درنتیجه مساحت جانبی منشور از روابط زیر به دست می‌‌آیند:

فرمول جبری مساحت جانبی منشور پنج‌‌پهلو که قاعده‌‌های آن پنج‌‌ضلعی منتظم است عبارت است از:

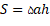
• a: طول یک ضلع پنج‌‌ضلعی
• h: ارتفاع منشور

مثال: مساحت جانبی منشور زیر را بیابید.

پاسخ: شکل بالا یک منشور پنج‌‌پهلوی منتظم است. بنابراین، از فرمول زیر مساحت جانبی آن را محاسبه می‌‌کنیم:

S=۵ah

• a=۶

• h=۱۳

مساحت جانبی منشور شش پهلو

واضح است که منشور شش‌‌پهلو منشوری است که از شش وجه جانبی ساخته شده است. اگر محیط قاعده یک منشور شش‌‌پهلو را در ارتفاع آن ضرب کنیم، مساحت جانبی به دست خواهد آمد. محیط قاعده این منشور محیط یک شش‌‌ضلعی است که می‌‌تواند منتظم یا نامنتظم باشد. اگر شش‌‌ضلعی منتظم باشد، آنگاه طول اضلاع قاعده یکسان خواهد بود. در این حالت، مساحت جانبی منشور از رابطه زیر محاسبه می‌‌شود:

اگر این فرمول را به‌‌صورت جبری بنویسیم داریم:

S=۶ah

• a: اندازه یک ضلع شش‌‌ضلعی
• h: ارتفاع منشور
در تصویر زیر گسترده یک منشور با قاعده‌‌هایی به‌‌شکل شش‌‌ضلعی منتظم را مشاهده می‌‌کنید.

مثال: یک منشور شش‌‌پهلو داریم که قاعده‌‌های آن به‌‌شکل شش‌‌ضلعی منتظم هستند. اگر ارتفاع منشور ۲۴ سانتی‌‌متر و اندازه هر ضلع شش‌‌ضلعی ۱۵ سانتی‌‌متر باشد، مساحت جانبی آن چقدر خواهد بود؟
پاسخ: از فرمول بالا کمک می‌‌گیریم و مقادیر را در آن جای‌‌گذاری می‌‌کنیم:

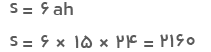
مساحت جانبی منشور برابر با ۲۱۶۰ سانتی‌‌متر مربع است.

فرمول کلی مساحت جانبی منشور منتظم

منشور منتظم منشوری است که قاعده‌‌های آن یک چندضلعی منتظم باشد. محیط یک چندضلعی منتظم با n ضلع که اندازه هر ضلع آن a است از رابطه زیر به دست می‌‌آید:

P= na

به‌‌این‌‌ترتیب، فرمول مساحت جانبی یک منشور منتظم با ارتفاع h به‌‌صورت زیر است:

S= nah

فرمول کلی مساحت جانبی منشور نامنتظم

اگر قاعده‌‌های یک منشور یک چندضلعی غیرمنتظم باشد، آن را منشور نامنتظم می‌‌نامند. محیط قاعده یک منشور n پهلو که طول اضلاع آن برابر نیست، عبارت‌‌اند از:

P = a_۱+a_۲+ ⋯ +a_n

a_۱ تا a_n اندازه ضلع اول تا ضلع nام چندضلعی است. درنتیجه مساحت جانبی یک منشور نامنتظم با ارتفاع h برابر است با:

S=(a_۱+a_۲+⋯a_n )h

مساحت جانبی مخروط

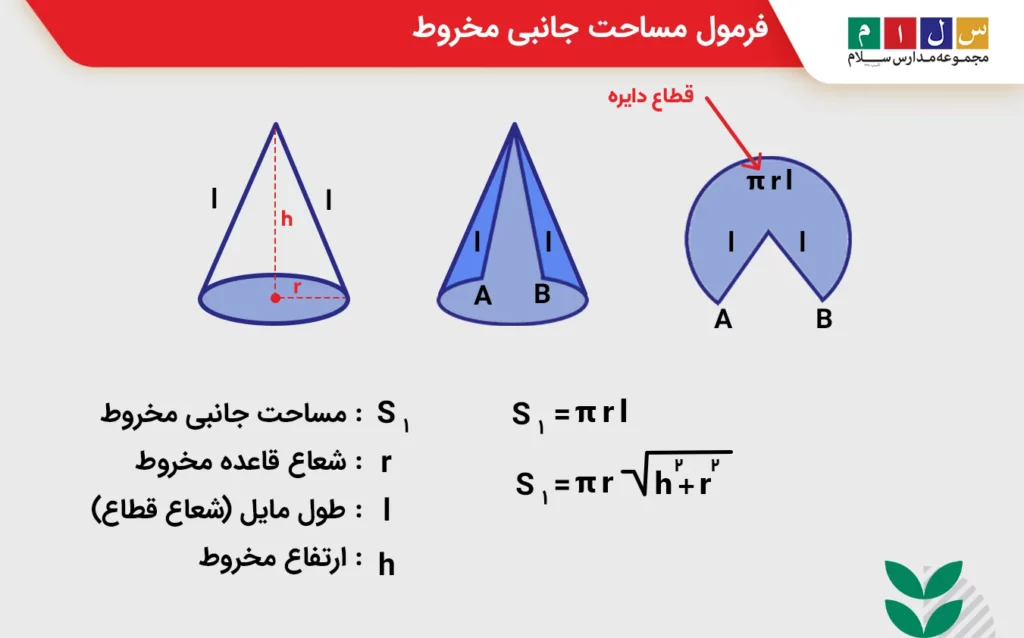
مخروط شامل دو وجه است؛ یک وجه دایره‌‌ای که قاعده نام دارد و یک وجه منحنی‌‌شکل که به آن وجه جانبی گفته می‌‌شود. وجه جانبی مخروط به‌‌شکل قطاعی از یک دایره است که در شکل گسترده زیر به‌‌خوبی دیده می‌‌شود. مساحت این قطاع که همان مساحت جانبی مخروط است برابر است با:

S=πrl

r: شعاع قاعده مخروط

l: طول مایل (شعاع قطاع)

اگر از قضیه فیثاغورس استفاده کنیم، می‌‌توانیم فرمول بالا را برحسب ارتفاع مخروط (h) و شعاع قاعده آن (r) نیز بنویسیم:

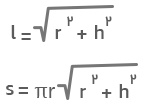
مساحت جانبی هرم

هرم یک چندوجهی است که از یک قاعده چندضلعی و چند وجه جانبی مثلثی به تعداد اضلاع قاعده تشکیل شده است. با توجه به اینکه وجه‌‌های جانبی یک هرم به‌‌شکل مثلث هستند، می‌‌توان مساحت جانبی هرم را با استفاده از فرمول مساحت مثلث محاسبه کرد.

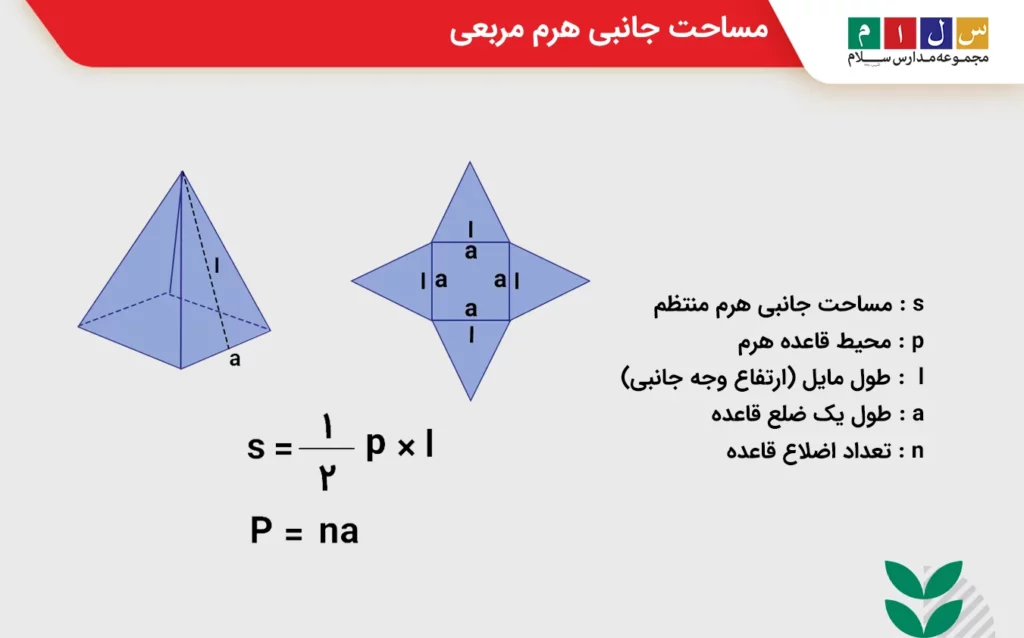
به‌‌عنوان مثال، اگر یک هرم با قاعده مربعی داشته باشیم، وجه جانبی آن شامل چهار مثلث یکسان خواهد بود که با محاسبه مساحت یکی از مثلث‌‌ها و ضرب آن در چهار می‌‌توان مساحت جانبی هرم را به دست آورد. در شکل زیر گسترده یک هرم مربعی را می‌‌توانید مشاهده کنید.

فرمول کلی مساحت جانبی در یک هرم منتظم با قاعده nضلعی به‌‌صورت زیر است:

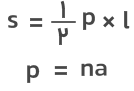
• S: مساحت جانبی هرم منتظم
• p: محیط قاعده هرم
• l: طول مایل (ارتفاع وجه جانبی)
• a: طول یک ضلع قاعده
• n: تعداد اضلاع قاعده

مثال: در یک هرم مربعی طول ضلع قاعده ۳ سانتی‌‌متر و ارتفاع وجه جانبی ۵ سانتی‌‌متر است. مساحت جانبی این هرم را حساب کنید.
پاسخ: هرم مربعی یک هرم منتظم است. بنابراین، مساحت جانبی آن را می‌‌توان به‌‌صورت زیر محاسبه کرد:

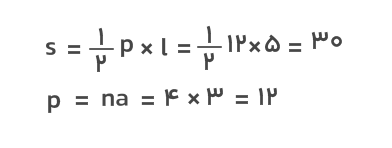
هرم مربعی تنها یکی از انواع هرم است. شما می‌‌توانید به‌‌عنوان تمرین، مساحت جانبی انواع دیگر هرم را محاسبه کنید.

تفاوت فرمول مساحت جانبی و مساحت کل

مساحت جانبی و مساحت کل از آن دسته مفاهیمی هستند که برخی دانش‌‌آموزان تفاوتی بین آن‌‌ها قائل نمی‌‌شوند و ممکن است آن‌‌ها را به‌‌جای یکدیگر به کار ببرند. ازاین‌‌رو، ما در این بخش می‌‌خواهیم تفاوت این دو را بیان کنیم تا برای همیشه آن را به خاطر بسپارید و بتوانید آن‌‌ها را از هم تشخیص دهید.
مساحت جانبی مساحت سطح‌‌های کناری یک حجم هندسی است؛ همان سطح‌‌های جانبی یا پهلوها که به قاعده‌‌ها وصل هستند، درصورتی که مساحت کل مساحت تمام وجه‌‌های حجم هندسی است که از مجموع مساحت وجه‌‌های تشکیل‌‌دهنده آن به دست می‌‌آید. برای مثال، فرمول مساحت کل در یک منشور به‌‌صورت زیر نوشته می‌‌شود:

این درحالی است که مساحت جانبی یک منشور از رابطه زیر تعیین می‌‌شود:

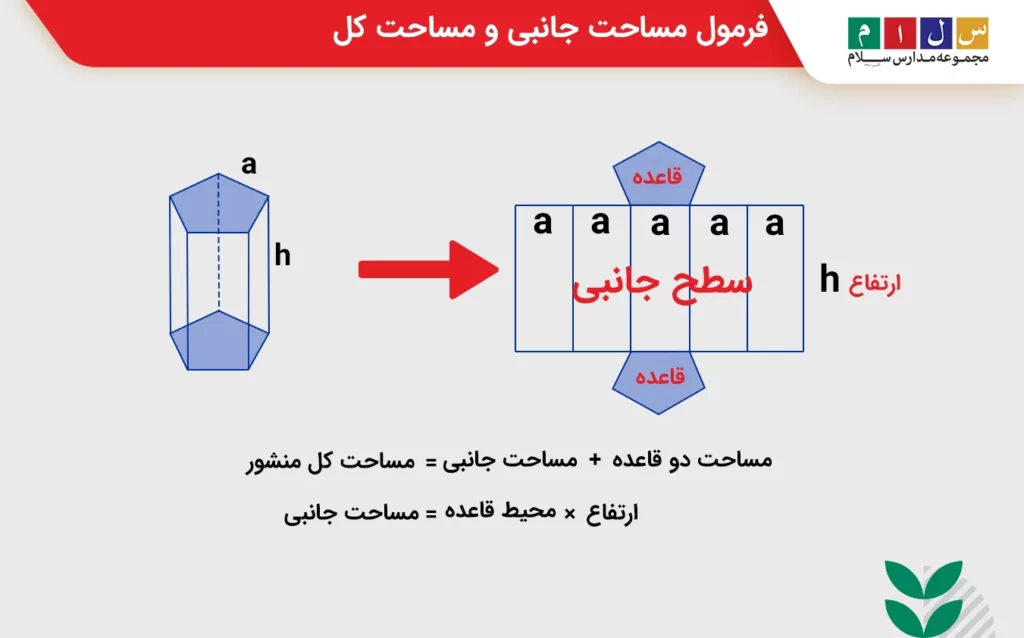
برای سایر اشکال سه‌‌بعدی نیز به‌‌همین صورت است. البته در هرم و مخروط تنها یک قاعده وجود دارد و به‌‌جای مساحت دو قاعده فقط کافی‌‌ست مساحت یک قاعده را به دست آوریم.

سخن پایانی

مساحت جانبی یک حجم هندسی برابر است با اندازه سطح جانبی آن. فرمول مساحت جانبی در اشکال مختلف متفاوت است که در این مقاله به آن‌‌ها پرداخته شد. توصیه می‌‌کنیم که برای به دست آوردن مساحت جانبی یک حجم هندسی به حفظ کردن فرمول آن اکتفا نکنید. قبل از هر چیز، مسئله و شکل داده‌‌شده را تجسم و درک کنید تا بتوانید به راه‌‌حل مناسب و درست برسید. حل تمرین‌‌های گوناگون در این زمینه به درک و فهم شما کمک خواهد کرد و قدرت تجسم شما را بهبود خواهد بخشید. امیدواریم این آموزش برایتان مفید بوده باشد.