فهرست مطالب
Toggleفرمول هرون را هرون اسکندرانی در حدود ۲هزاره پیش، در کتاب معروف خود بهنام «متریکها» آورده است. با فرمول هرون، بدون داشتن ارتفاع مثلث میتوان مساحتش را حساب کرد. مساحت انواع مثلثها و حتی دیگر چندضلعیها بهکمک فرمول هرون محاسبهپذیر است. ما در این مقاله قصد داریم کاربرد این فرمول در محاسبه مساحت مثلث و چهار ضلعیها را با مثال توضیح دهیم.
فرمول هرون چیست؟
فرمولی برای محاسبه مساحت تمام مثلثها است؛ فقط کافیست اندازه ۳ ضلع مثلث را داشته باشیم و طبق مراحل زیر پیش برویم:
- نصف محیط مثلث را بهکمک فرمول زیر حساب کنیم:
s = (a+b+c) ÷۲
- s: نصف محیط مثلث
- a، b و c: اندازه ۳ ضلع مثلث
- اندازه نصف محیط مثلث (s) و ۳ ضلع آن را در فرمول زیر جایگذاری میکنیم:
( A= √ (s (s-a) × (s-b) × (s-c)
در فرمول بالا، A حرف اول کلمه Area و بهمعنای مساحت است. همانطور که میبینید، در فرمول هرون نیازی به ارتفاع یا اندازه زوایای مثلث نداریم. تنها چیزی که برای بهکارگرفتن این فرمول نیاز داریم، اندازه ضلعهای مثلث است.
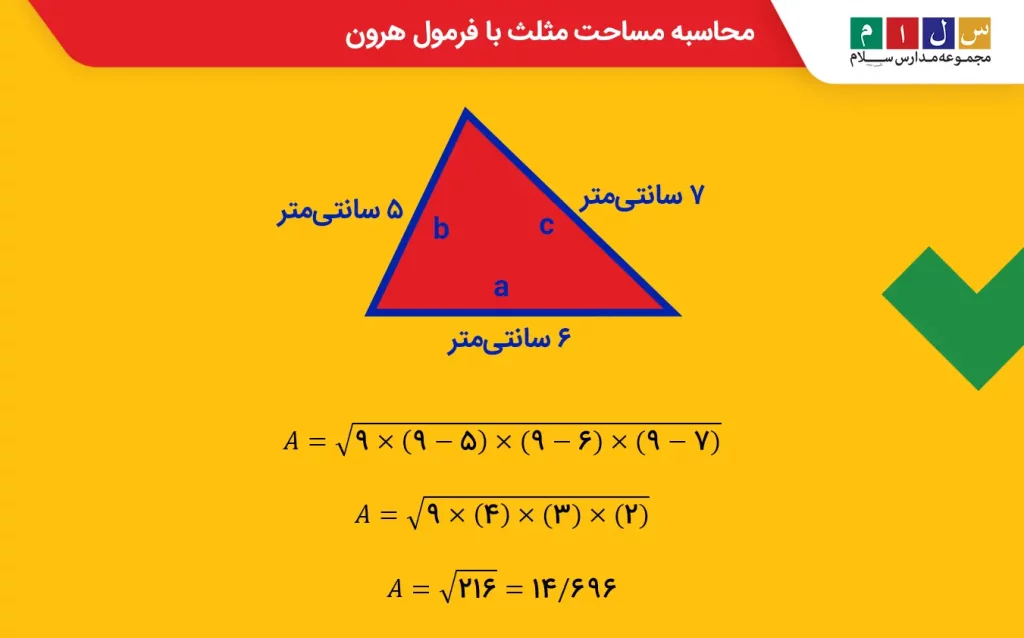
مثال: اگر ۳ ضلع مثلثی بهترتیب ۵، ۶ و ۷ سانتیمتر باشند، مساحت آن را حساب کنید.جواب: اندازه ۳ ضلع مثلث (a، b و c) را داریم. در مرحله اول آنها را در فرمول محاسبه نصف محیط مثلث میگذاریم:
s = (۵ + ۶ + ۷) ÷ ۲= ۱۸ ÷ ۲ = ۹
حالا که اندازه نصف محیط مثلث (s) را به دست آوردیم، آن را در فرمول هرون میگذاریم.
( A= √ (۹ × (۹ – ۵) × (۹ – ۶) × ( ۹ – ۸)
( A= √ (۹ × (۴) × (۳) × ( ۲)
۱۴/۶۹۶ = A= √۲۱۶
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
فرمول هرون برای محاسبه مساحت چهارضلعی
فرمول هرون برای محاسبه مساحت ۴ ضلعیها هم کاربرد دارد، زیرا همه ۴ ضلعیها قابل تبدیل به ۲ مثلث هستند. مثلا فرض کنید یک لوزی با ۴ راس ABCD داریم که:
راس A به C وصل شده و قطر لوزی را نشان میدهد که برابر با e است.
اندازه هر کدام از ضلعهای آن برابر با a، b، c و d است.

همانطور که در تصویر بالا میبینید، هر ۴ ضلعی ۲ مثلث است. حالا اگر مساحت این ۲ مثلث را با هم جمع بزنیم، مساحت ۴ ضلعی به دست میآید. پس طبق این قاعده خواهیم داشت:
(A =√ (s (s – a) × (s – d) × (s – e) ) + √(s (s – b) × (s -c) × ( s – e )
محاسبه مساحت چهارضلعیها را میتوانید در مقالههای اختصاصی هریک بخوانید:
مساحت مربع – مساحت لوزی – مساحت ذوزنقه – مساحت متوازی الاضلاع
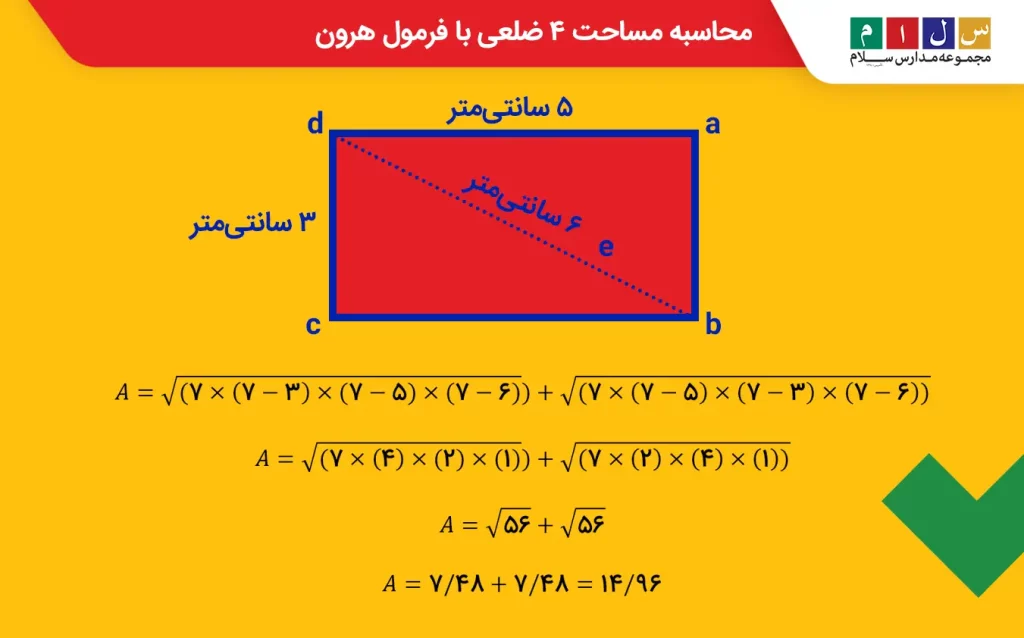
مثال: اگر یک مستطیل با ضلعهای a، b، c و d داشته باشیم که اندازه ضلعهای آن بهترتیب ۳، ۵، ۳ و ۵ سانتیمتر باشند و اندازه قطر آن (e) ۶ سانتیمتر باشد، مساحت مستطیل را بهکمک فرمول هرون محاسبه کنید: جواب: برای محاسبه مساحت ۴ ضلعی به کمک فرمول هرون، باید اندازه ۲ مثلث درون آن را محاسبه و با هم جمع کنیم. البته قبل از آن باید اندازه نصف محیط مثلث را حساب کرده باشیم:
s = (۳ + ۵ + ۶) ÷ ۲ = ۱۴ ÷ ۲ = ۷
کاربردهای فرمول هرون
از فرمول هرون در زمینههای مختلفی میتوان استفاده کرد، مانند:
- تعیین مساحت انواع مثلث، اگر اندازه ۳ ضلع آن را داشته باشیم.
- محاسبه مساحت ۴ ضلعی بهکمک تبدیل آن به ۲ مثلث و جمع مساحت ۲ مثلث با یکدیگر.
- تعیین اندازه مساحت انواع چندضلعیها از طریق تبدیل آنها به چند مثلث و جمع مساحت آن مثلثها با یکدیگر.
سخن پایانی
فرمول هرون برای محاسبه مساحت انواع مثلث کاربرد دارد. این فرمول قدمت بسیار زیادی دارد و نزدیک به ۲۰۰۰ سال پیش کشف شده است. برای استفاده از این فرمول باید اندازه ۳ ضلع مثلث و نصف محیط آن را داشته باشیم. از فرمول هرون برای محاسبه مساحت دیگر چندضلعیهای منتظم و نامنتظم هم میتوان استفاده کرد؛ البته به شرط اینکه آن چندضلعی را به ۲ یا چند مثلث تبدیل کنیم، مساحت هر کدام از مثلثها را اندازه بگیریم و سپس همه آنها را با هم جمع کنیم.
سوالات متداول
- فرمول هرون چیست؟
جذرِ (نصف محیط مثلث × تفاضل نصف محیط مثلث از ضلع اول × تفاضل نصف محیط مثلث از ضلع دوم × تفاضل نصف محیط مثلث از ضلع سوم)؛ یا( A= √ (s (s-a) × (s-b) × (s-c). - فرمول هرون چه کاربردهایی دارد؟
بیشترین کاربرد این فرمول برای محاسبه مساحت مثلث است، اما چون دیگر اشکال هندسی را هم میتوان به چند مثلث تبدیل کرد، پس این فرمول برای محاسبه دیگر اشکال هندسی هم قابل استفاده است.









