فهرست مطالب
Toggleدر بین اتحادهای مهم ریاضی، اتحاد جمله مشترک از دروس بسیار مهمی است. این اتحاد در سادهسازی عبارتهای جبری، حل معادلات درجه دوم و حتی تجزیه چندجملهایها به کار میرود. آشنایی با آن مسیر بخش کردن، سادهسازی و تجزیه را بسیار سریعتر میکند و به همین دلیل در کتابهای درسی و فرمول اتحاد مشترک نهم اهمیت زیادی دارد. در این مطلب مدارس سلام همهچیز درباره اتحاد جمله مشترک را از تعریف، فرمول، اثبات، کاربرد و حتی نمونه سوال اتحاد جمله مشترک با مثال در اختیارتان قرار خواهیم داد.
اتحاد در ریاضیات چیست؟
در ریاضیات اتحاد به معادلهای گفته میشود که در آن، برابری دو طرف معادله برای همه مقادیر متغیرها برقرار است. به عبارت دیگر، اگر متغیر موجود در معادله هر عددی در نظر گرفته شود، باز هم دو طرف تساوی برابر خواهند بود. برای نمونه، اتحاد معروف زیر را بررسی کنید:
(a-b)(a+b)=a۲-b۲
این یک اتحاد مزدوج محسوب میشود. در مجموع اتحاد چاق و لاغر، اتحاد مزدوج، اتحاد مربع و اتحاد مکعب از مهمترین اتحادهای ریاضی به حساب میآیند.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
اتحاد جمله مشترک چیست؟ | آموزش اتحاد جمله مشترک
اتحاد جمله مشترک یکی از اتحادهای مهم جبر است که زمانی کاربرد دارد که دو عبارت دوجملهای یک جمله مشترک داشته باشند.
فرم کلی آن بهصورت زیر نوشته میشود:
(x + a)(x + b) = x۲ + (a + b)x + ab
در این اتحاد:
- x جمله مشترک است.
- a و b اعداد یا عبارات غیرمشترک هستند.
- (x + a) و (x + b) دو دوجملهای هستند که یک جمله مشترک دارند.
بر اساس این رابطه، حاصل ضرب دو دوجملهای مشابه همیشه به یک سهجملهای تبدیل میشود که شامل توان دوم جمله مشترک، جمع عددهای غیرمشترک در کنار جمله مشترک و در نهایت حاصل ضرب آن دو عدد است.
این اتحاد به آسانی قابل اثبات بوده و اگر در سمت چپ پرانتزها اعداد را در یکدیگر ضرب کنید، سمت راست تساوی به دست خواهد آمد.
فرمول اتحاد جمله مشترک
اگرچه فرمول اتحاد جمله مشترک به سادگی فرمول اتحاد چاق و لاغر نیست، اما از مواردی با فرمول ساده محسوب میشود. به همین دلیل حفظ کردن آن برای بسیاری از دانشآموزان آسان است. این فرمول در تفاضل و مجموع به شرح زیر است:
(x+a) (x+b) = x۲+(a+b)x+ab
البته با این حال اگر این فرمول از آن دسته اتحادهایی است که هر کار میکنید در ذهنتان ثبت نمیشود، این ترفند آموزش اتحاد جمله مشترک به شما در حفظ کردن فرمول کمک میکند:
- ترفند: توان، جمع، ضرب
- اول جمله مشترک که x است به توان دوم میرود: x۲
- سپس جمع دو جمله غیرمشترک در کنار این نوشته میشود: (a+b)x
- مرحله آخر هم ضرب دو جمله غیرمشترک قرار میگیرد: ab
سایر شکل های اتحاد جمله مشترک دو جمله ای
اگر در امتحان با عبارت اتحاد جمله مشترک دو جمله ای مواجه شدید، نگران نباشید! این همان فرمولی است که پیشتر ذکر کردیم. اگر علامت مثبت و منفی در این جمله تغییر کند، این فرمول در حالتهای دو جمله ای زیر هم نوشته خواهد شد:
(x – a)(x + b) = x۲ + (b – a)x – ab
(x + a)(x – b) = x۲ + (a – b)x – ab
(x – a)(x – b) = x۲ – (a + b)x + ab
اگر این فرمولها و در مجموع اتحاد جمله مشترک با ضریب برای شما دشوار به نظر میرسد، با مطالعه روش اثبات و مثالها آن را بهتر یاد خواهید گرفت.
نمونه سوال اتحاد جمله مشترک نهم با جواب:
حاصل ضرب (1+x) در (4+x) را به دست آورید.
هر یک از این دو، دو تک جملهای هستند. در نتیجه میتوانیم آنها را یک دوجملهای بدانیم و x هم در هر دو مشترک است. از این رو امکان استفاده از اتحاد جمله مشترک دو جمله ای وجود دارد:
(x+a)(x+b)=x۲+(a+b)x+ab
بر اساس مسئله در اینجا به این شرح است:
a=۱
b=۴
با جایگذاری در اتحاد، این معادله به دست میآید:
(x + ۱)(x + ۴) = x۲ + (۱ + ۴)x +۱× ۴
(x + ۱)(x + ۴) = x۲ + ۵x +۴
در نتیجه جواب معادله به آسانی از طریق اتحاد جمله مشترک به دست آمد.
اتحاد جمله مشترک سه جمله ای
این اتحاد زمانی به کار میرود که سه دوجملهای پشت سر هم ضرب شوند و همه آنها یک متغیر مشترک یعنی x داشته باشند. در این حالت، سه عدد یا عبارت غیرمشترک (a و b و c) متغیر قرار میگیرند. فرمول اتحاد جمله مشترک سه جمله ای به این شرح است:
(x + a)(x + b)(x + c)
=
x۳ + (a + b + c)x۲ + (ab + ac + bc)x + abc
ساختار نتیجه را میتوان مرحله به مرحله به این صورت به خاطر سپرد:
- ابتدا جمله مشترک (x) به توان سه میرود: x۳
- سپس مجموع a و b و c در کنار x۲ قرار میگیرد: (a + b + c)x۲
- بعد مجموع حاصل ضرب دوتاییها نوشته میشود: (ab + ac + bc)x
- در پایان، حاصل ضرب سه عدد غیرمشترک قرار میگیرد: abc
اثبات اتحاد جمله مشترک
اثبات اتحاد جمله مشترک به دو روش بهصورت مستقیم و یا با شکل انجام میشود که در این بخش هر دو را توضیح دادهایم.
اثبات اتحاد جمله مشترک مستقیم
برهان مستقیم بسیار آسان است و تنها باید سمت چپ را سادهسازی کنید. این فرمولی است که باید ثابت شود:
(x+a)(x+b)=x۲+(a+b)x+ab
ابتدا سمت چپ را باز میکنیم:
(x + a)(x + b) = x·x + x·b + a·x + a·b
پس از سادهسازی به این ترتیب میشود:
x۲ + bx + ax + ab
در این مرحله باید فاکتورگیری و جمع انجام دهیم که x در هر دو جمله bx و ax مشترک است و فاکتور گرفته میشود. نتیجه همان اثبات است:
x۲ + (a + b)x + ab
اثبات اتحاد جمله مشترک هندسی
برای اثبات هندسی، کافی است مفهوم مساحت را در نظر بگیریم. فرض کنید یک مستطیل داریم که:
- طول آن برابر با (x + a)
- عرض آن برابر با (x + b)

مساحت این مستطیل از ضرب طول در عرض به دست میآید:
(x + a)(x + b)
حالا مستطیل را به چهار بخش کوچک تقسیم میکنیم:
- مربع مرکزی با ضلع x : مساحت x۲
- مستطیل سمت راست با ابعاد x و a : مساحت ax
- مستطیل بالا با ابعاد x و b : مساحت bx
- مستطیل کوچک گوشه با ابعاد a و b : مساحت ab
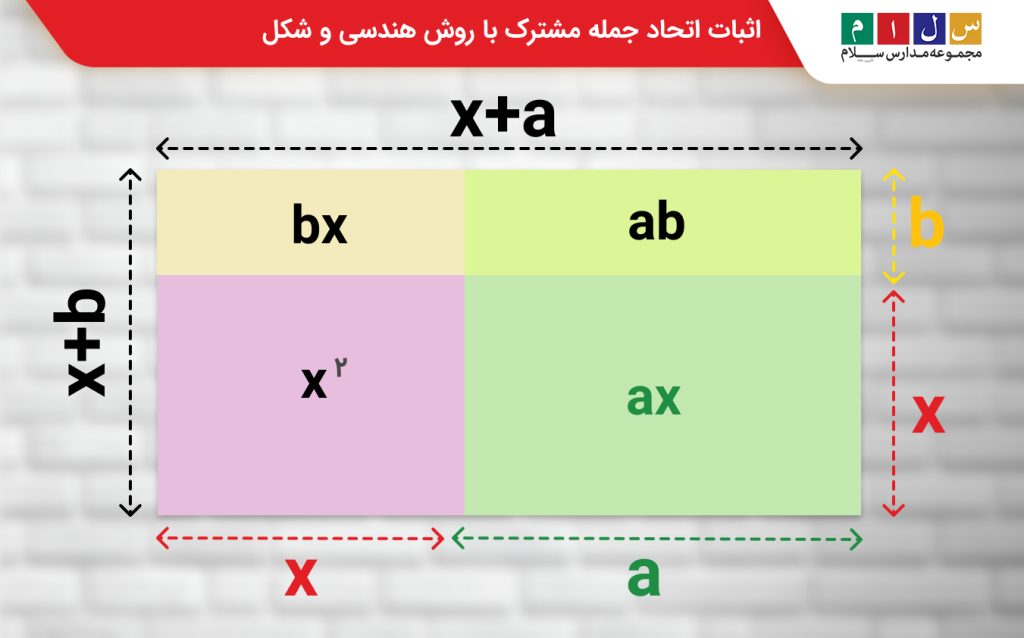
با جمع کردن مساحت همه بخشها داریم:
x۲ + ax + bx + ab
در مرحله بعد جملات مشابه ax و bxرا جمع و فاکتورگیری میکنیم:
x۲ + (a + b) x + ab
همانطور که میبینید، حاصل ضرب دو دوجملهای دقیقاً به شکل اتحاد جمله مشترک در میآید و اثبات به آسانی کامل میشود.
پیشنهاد مطالعه: مساحت مثلث مختلف الاضلاع
کاربرد اتحاد جمله مشترک
اتحاد جمله مشترک یکی از ابزارهای قدرتمند ریاضی است که به ما کمک میکند عبارتهای جبری را راحتتر بازنویسی، سادهسازی و تجزیه کنیم. با استفاده از این اتحاد میتوان ضرب دو دوجملهای یا سه دوجملهای را به شکل سادهتر نوشت و مراحل حل مسائل را کوتاهتر کرد.
اتحاد جمله مشترک در تجزیه عبارت جبری
یکی از کاربردهای مهم، تجزیه معادلات درجه دو است. با استفاده از اتحاد جمله مشترک میتوان معادله را به صورت حاصل ضرب دو جمله ساده نوشت.
- مثال:
معادله زیر را تجزیه کنید:
x۲ + ۷x + ۱۰
در ابتدا به فرم استاندارد و فرمول اتحاد جمله مشترک نیاز داریم:
(x+a)(x+b)=x۲+(a+b)x+ab
سپس سمت راست اتحاد جمله مشترک با مقایسه معادله موجود در سؤال به این ترتیب میشود:
x۲+(a+b)x+ab
x۲ + ۷x + ۱۰
بر این اساس، تنها تفاوت ضرایب آنها هستند. سپس میدانیم دو عددی که جمع آنها 7 و حاصل ضربشان۱۰ باشد، ۵ و ۲ است. در نتیجه:
x۲+ ۷x + ۱۰= (x + ۵)(x + ۲)
پیشنهاد مطالعه: آموزش جمع و تفریق ذهنی
اتحاد جمله مشترک در سادهسازی
با کمک اتحاد جمله مشترک، عبارتهای جبری پیچیده را سادهتر نوشت.
- مثال:
عبارت زیر را ساده کنید:
(a + ۲)۲ – (a − ۳)(a + ۴)
ابتدا اتحاد مربع مجموع دوجملهای به این شرح است:
(a + ۲)۲ = a۲ + ۴a + ۴
اتحاد جمله مشترک بالا به این ترتیب میشود:
(a – ۳)(a + ۴) = a۲ + a – ۱۲
سپس جایگذاری در عبارت اصلی سؤال را انجام میدهیم:
(a۲ + ۴a + ۴) – (a۲ + a – ۱۲) = ۳a + ۱۶
اتحاد جمله مشترک در حل و ریشهگیری معادلات
همانطور که میدانید، از روشهای گوناگونی برای حل معادلات درجه دو استفاده میشود که فاکتورگیری، مربع کامل و دلتا از آنها هستند. در فاکتورگیری، از اتحادها و از جمله فرمول اتحاد جمله مشترک نهم هم استفاده میشود چراکه پس از تجزیه، ریشههای معادله به راحتی به دست میآیند.
- مثال:
معادله زیر را حل کنید:
x۲ + ۸x + ۱۵ = ۰
دو عدد پیدا میکنیم که جمعشان برابر ۸ و حاصل ضربشان برابر ۱۵ باشد:۳ و ۵
معادله را تجزیه میکنیم:
x۲ +۸x + ۱۵= (x + ۳)(x + ۵)
هر جمله را برابر صفر قرار میدهیم:
x + ۳ = ۰ → x = -۳
x + ۵ = ۰ → x = -۵
به این ترتیب ریشهها برابر -۵ و -۳هستند.
اتحاد جمله مشترک به انگلیسی
اتحاد جمله مشترک در انگلیسی اصطلاحی مستقیم ندارد، اما میتوان آن را در چارچوب «Factorization Identities» یا «Binomial Theorem Identities» دستهبندی کرد. این اتحاد در منابع مختلف، گاه با عنوان «Identity IV» و گاه «Identity VI» آمده است که نشاندهنده کاربرد آن در بازنویسی و تجزیه عبارات جبری به صورت دو جملهای است.
سخن پایانی
اتحاد جمله مشترک اتحادی به نسبت ساده و کاربردی در جبر است که با آن امکان شناسایی جملههای مشترک و بازنویسی عبارات پیچیده وجود دارد، سرعت محاسبات را افزایش میدهد و برای تجزیه و حل معادلات درجه دو استفاده میشود. استفاده از این اتحاد روند حل مسائل را روانتر میکند و به دانشآموز کمک میکند تا با راحتی بیشتری مراحل محاسبات را پیش ببرد.
سؤالات متداول
- فرمول اتحاد جمله مشترک به فارسی چیست؟
جمله مشترک به توان دو به علاوه ضرب مجموع جملات غیرمشترک در مشترک و به علاوه ضرب جملات غیرمشترک در هم میشود. - اتحاد جمله مشترک سه جمله ای چیست؟
این اتحاد که در مطلب فرمول آن را شرح دادهایم، حاصل ضرب سه دوجملهای است. - از فرمول اتحاد جمله مشترک در کجا استفاده میشود؟
در تعیین حاصل ضرب دوجملهای، تجزیه و ریشهگیری معادلات کاربرد دارد.









