فهرست مطالب
Toggleکسرها بخشهای مساوی از یک کل یا مجموعه را نشان میدهند و از دو بخش صورت و مخرج ساخته شدهاند.
برای مثال، کسر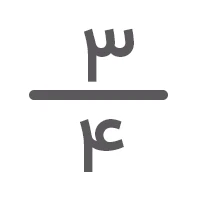
در این آموزش، با مفهوم تساوی کسرها آشنا خواهیم شد و روش بهدست آوردن کسرهای مساوی را توضیح خواهیم داد.
کسر مساوی چیست؟
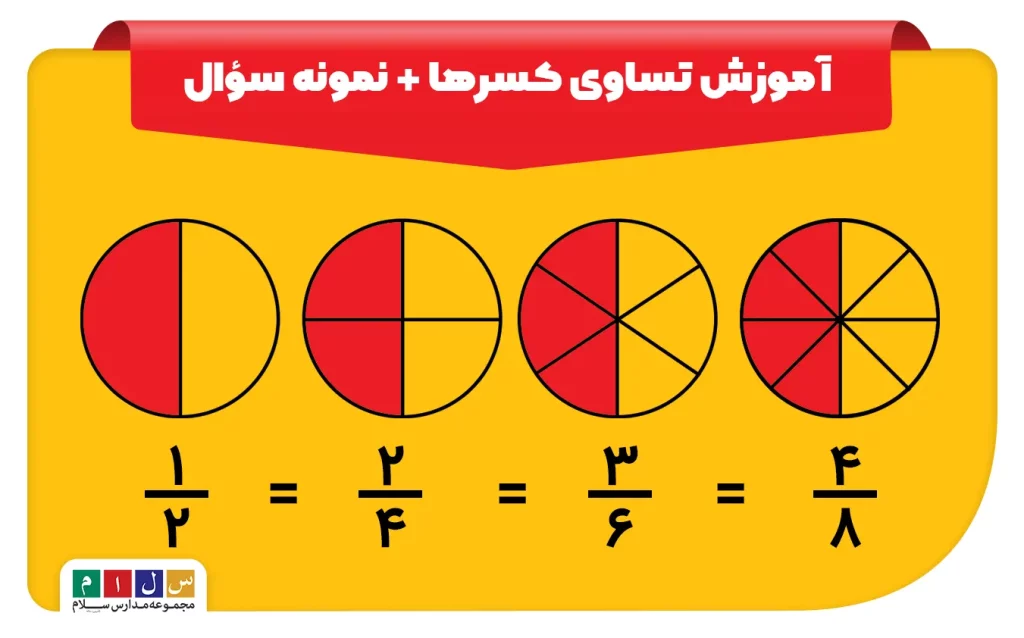
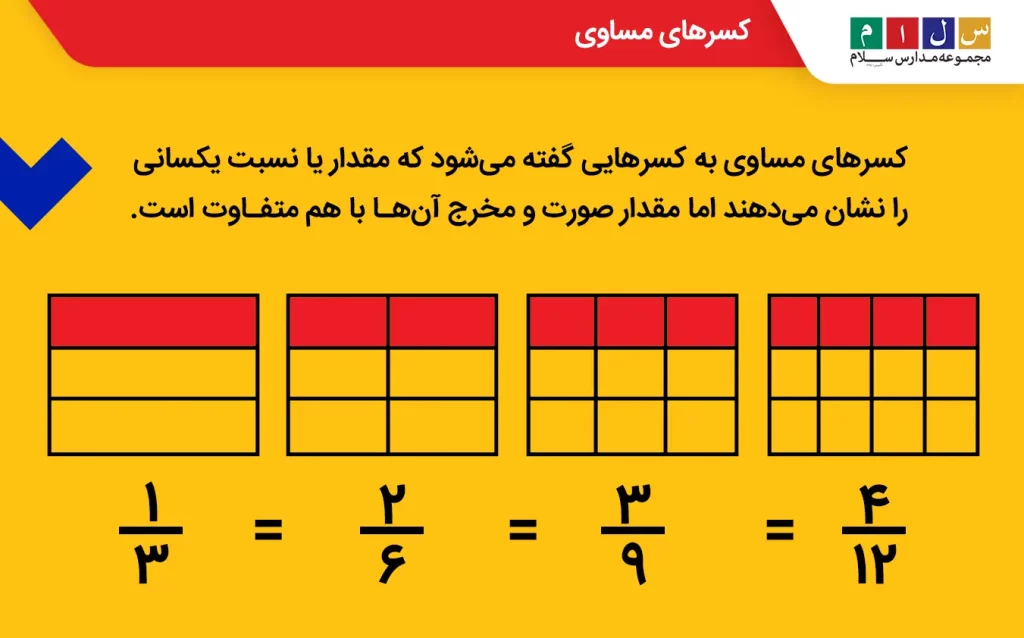
کسرهای مساوی به کسرهایی گفته میشود که مقدار یا نسبت یکسانی را نشان میدهند اما مقدار صورت و مخرج آنها با هم متفاوت است. چنین کسرهایی بعد از سادهسازی همگی به یک کسر یکسان یا معادل تبدیل میشوند.
برای مثال، همانطور که در تصویر زیر هم نشان داده شده است، کسرهای 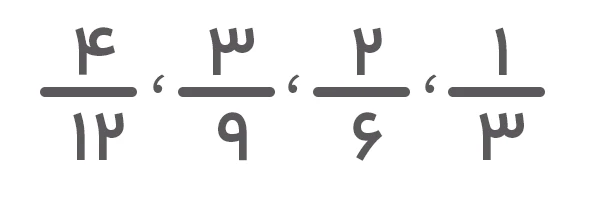

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
چگونه کسرهای مساوی را به دست آوریم؟
برای یافتن کسرهای مساوی کافیست صورت و مخرج را در یک عدد ضرب یا بر یک عدد تقسیم کنیم. بنابراین، از دو طریق ضرب و تقسیم میتوانیم کسرهای معادل یا مساوی را بهدست آوریم. در ادامه هر دو روش را با مثال توضیح خواهیم داد.
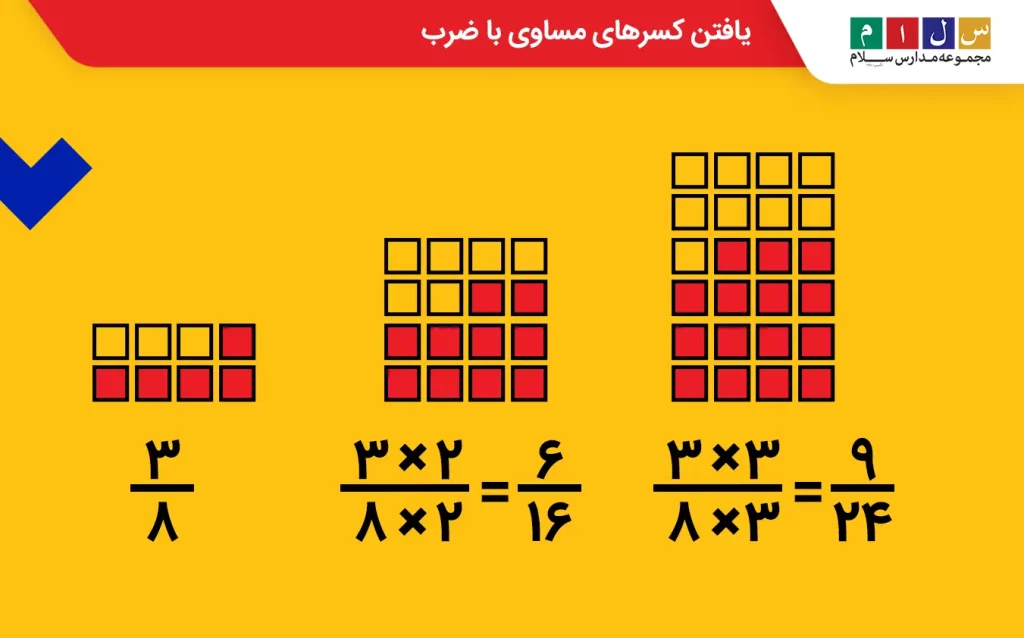
به دست آوردن کسرهای مساوی با ضرب
فرض کنید میخواهیم کسرهای معادل 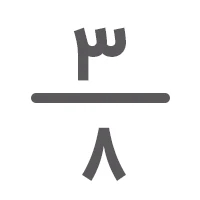
بنابراین، دو کسر 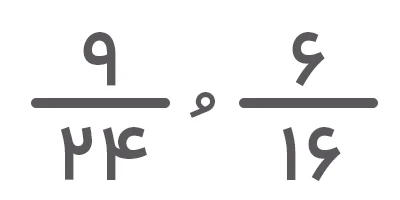

پیشنهاد مطالعه: آموزش ضرب کسرها به زبان ساده
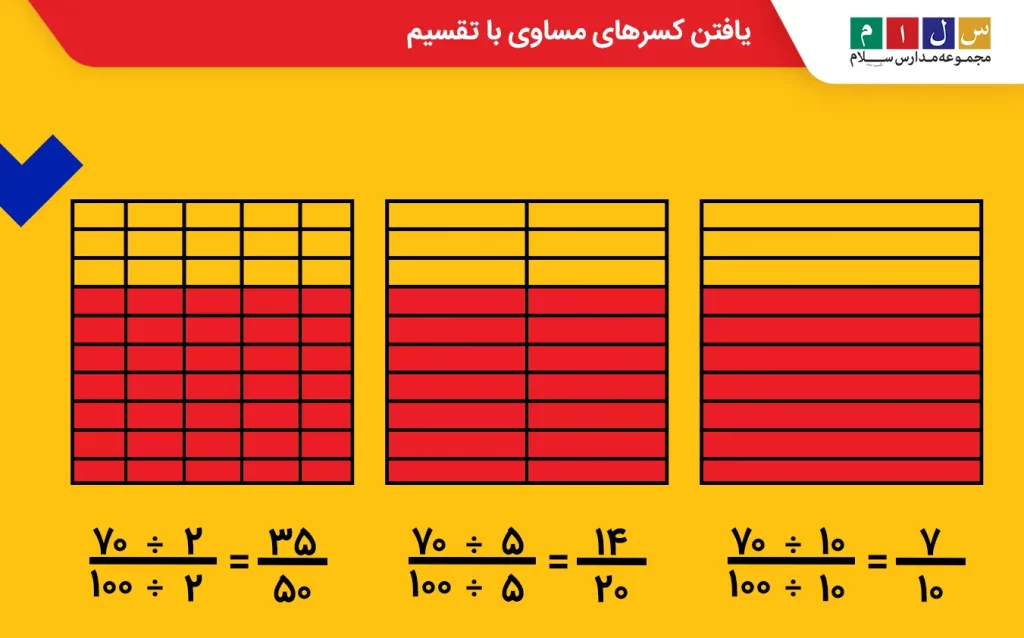
به دست آوردن کسرهای مساوی با تقسیم
در این روش، صورت و مخرج کسر موردنظر را بر یک عدد تقسیم میکنیم تا کسرهای مساوی با آن بهدست آید. پیشنهاد می کنم برای یادگیری بیشتر تقسیم این کار به مقاله تقسیم کسرها مراجعه کنید.
کسرهای مساوی با 
ابتدا اعدادی را که هم ۷۰ و هم ۱۰۰ بر آنها بخشپذیرند یعنی همان عاملها یا بزرگترین مقسومعلیه مشترک ۷۰ و ۱۰۰ را پیدا میکنیم. عاملهای مشترک این دو عدد ۲، ۵ و ۱۰ است. بنابراین، هم صورت و هم مخرج را بر این اعداد تقسیم میکنیم تا کسرهای معادل مشخص شوند.
پس میتوان نوشت:
چگونه تساوی کسرها را تشخیص دهیم؟
روشهای مختلفی برای بررسی مساوی بودن یا نبودن کسرها وجود دارد. این روشها عبارتاند از:
- یکسان کردن مخرج کسرها
- تعیین عدد اعشاری معادل کسرها
- طرفین وسطین
- رسم شکل
بررسی تساوی کسرها با یکسان کردن مخرج ها
در این روش، برای تشخیص مساوی بودن دو یا چند کسر کافیست مخرجهای آنها را برابر کنیم یا بهعبارتی مخرج مشترک بگیریم.
برای مخرج مشترک گرفتن نیز باید ک م م (کوچکترین مضرب مشترک) را تعیین کنیم. بهعنوان مثال، برای بررسی تساوی دو کسر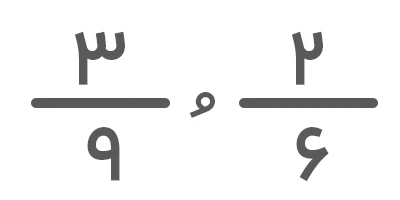
[۶, ۹ ] = ۱۸
حالا که ک م م مشخص شد، باید کاری کنیم که مخرجها مساوی ۱۸ شوند. به همین منظور، صورت و مخرج کسر 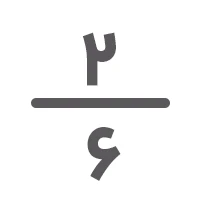
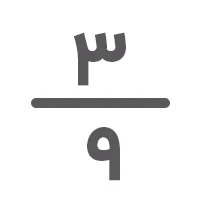
همانطور که میبینید، هر دو کسر مساوی با 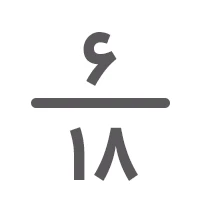

دو کسر مساویاند.
نکته: اگر پس از مخرج مشترک گرفتن، صورت کسرها نابرابر بود، یعنی کسرها نامساوی هستند. در این حالت، میتوانیم با نگاه کردن به مقدار صورت کسرها کسر بزرگتر وکوچکتر را تشخیص دهیم. پس میتوان از این روش برای مقایسه کسرها نیز استفاده کرد.
بررسی تساوی کسرها با تعیین عدد اعشاری معادل
روش دیگری که میتوان با کمک آن تساوی کسرها را تعیین کرد، تبدیل کسرها به اعداد اعشاری یا بهعبارتی نوشتن اعداد اعشاری معادل با کسرهای موردنظر است. برای مثال، عدد اعشاری معادل کسرهای 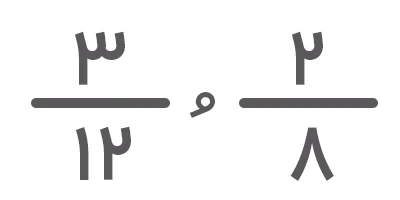
ازآنجا که شکل اعشاری کسرها یکسان است، این دو کسر معادل هم هستند.
بررسی تساوی کسرها با طرفین وسطین
در روش طرفین وسطین، صورت کسر اول را در مخرج کسر دوم و صورت کسر دوم را در مخرج کسر اول ضرب میکنیم. اگر حاصلضرب هر دو با هم برابر باشد، آنگاه کسرها مساوی هستند.
در تصویر زیر، مراحل بررسی تساوی دو کسر با روش طرفین وسطین نشان داده شده است.

بررسی تساوی کسرها با شکل
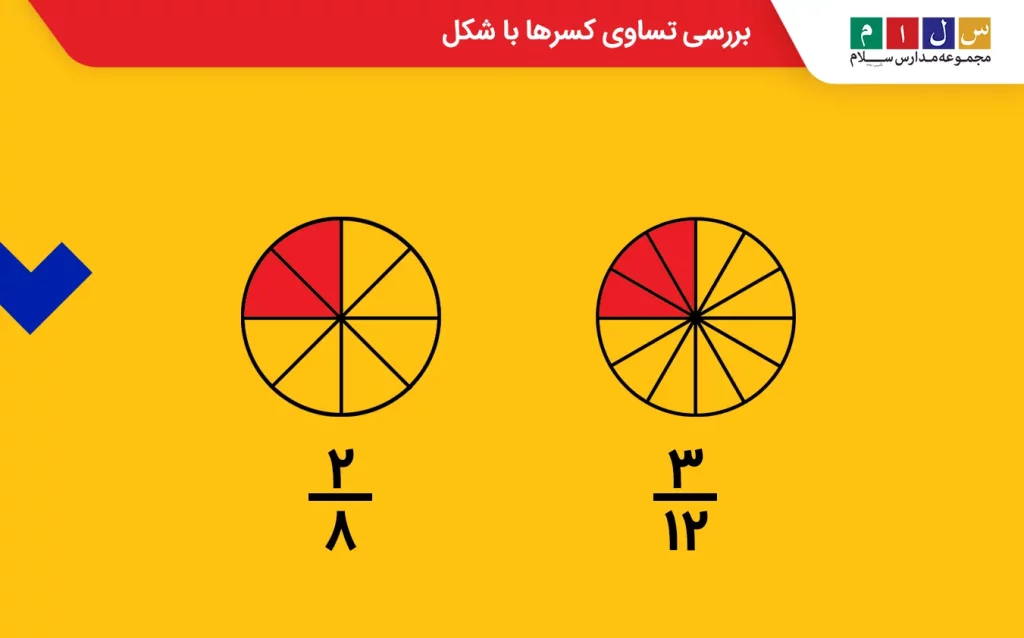
کسرهای را در نظر بگیرید. میخواهیم با رسم شکل بررسی کنیم که آیا این دو کسر با هم مساوی هستند یا نه. برای این کار، دو شکل یکسان مانند تصویر زیر رسم میکنیم و کسرهای موردنظر را روی آنها نمایش میدهیم. اگر قسمتهای رنگشده در هر دو شکل مقدار یکسانی را نشان دادند، آنگاه هر دو کسر با هم برابرند.
همانطور که میبینید بخشهای رنگی هر دو شکل مقدار یکسانی را نشان میدهند. این یعنی اینکه کسرهای با هم مساویاند.
نمونه سؤال تساوی کسرها
سؤال ۱: جاهای خالی در تصویر زیر را پر کنید.
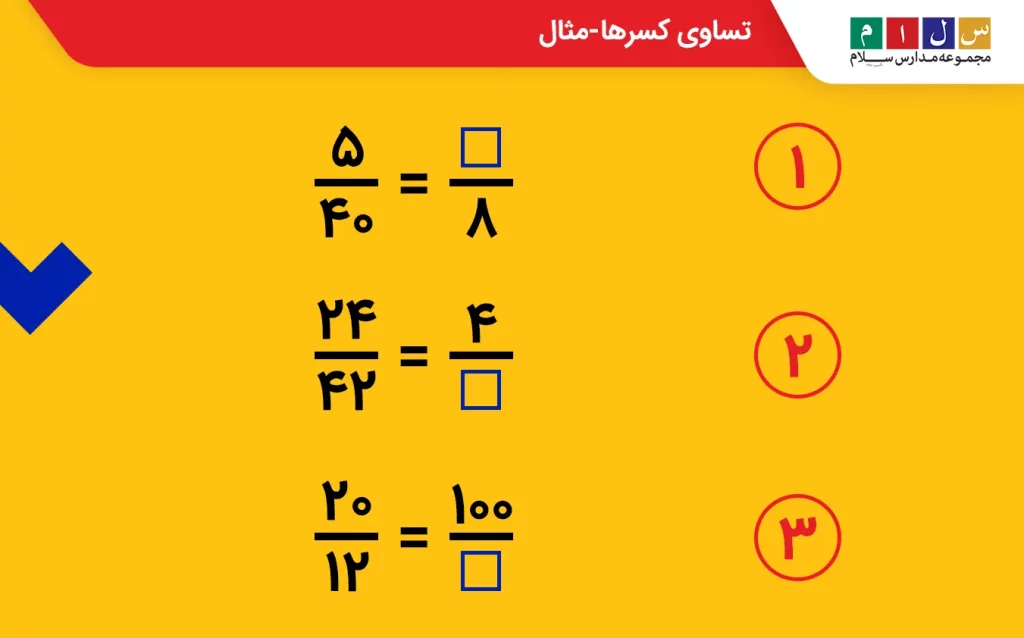
جواب: با استفاده از روشهایی که در بخشهای قبل درمورد آنها توضیح دادیم، مقادیر نامعلوم را بهدست میآوریم.
در تساوی شماره ۱ رابطه بین مخرج کسر اول و دوم به این صورت است که مخرج کسر دوم یعنی ۸ یکپنجم مخرج کسر اول یعنی ۴۰ است. بنابراین، چون دو کسر باید مساوی باشند، باید مقدار صورت کسر دوم نیز یکپنجم صورت کسر اول باشد. یعنی باید صورت کسر اول را بر ۵ تقسیم کنیم. خواهیم داشت:
در تساوی شماره ۲ صورت کسر اول یعنی ۲۴ بر ۶ تقسیم شده و حاصل آن ۴ شده است. پس باید مخرج یعنی ۴۲ را هم بر ۶ تقسیم کنیم تا مقدار نامعلوم تعیین شود.
در تساوی شماره ۳ صورت کسر دوم ۵ برابر صورت کسر اول است بنابراین برای مشخص شدن مقدار مجهول کافیست مخرج کسر اول را در ۵ ضرب کنیم. خواهیم داشت:
سؤال ۲: آیا کسرهای زیر مساوی هستند؟
جواب: برای پاسخ به این سؤال روشهای مختلفی را میتوان بهکار برد. ما در اینجا از روش یکسان کردن مخرجها با کمک ک م م استفاده میکنیم. ابتدا کوچکترین مضرب مشترک ۱۷ و ۵۱ را مییابیم. کوچکترین مضرب مشترک این دو عدد، ۵۱ است. پس باید مخرج کسرها را تبدیل به ۵۱ کنیم. با توجه به اینکه مخرج کسر دوم ۵۱ است، دیگر نیازی به تغییر دادن مقادیر این کسر نداریم اما مخرج کسر اول را باید بهشکل زیر به ۵۱ تبدیل کنیم.
همانطور که مشاهده میکنید، کسر بهدستآمده مساوی با کسر دوم در صورت سؤال است. این نشان میدهد که دو کسر دادهشده مساوی هستند.
سؤال ۳: سه کسر مساوی با کسر 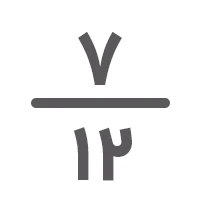
جواب: برای بهدست آوردن کسرهای مساوی با کسر 
سخن پایانی
کسرهای مساوی دارای صورت و مخرجهایی با مقادیر متفاوت هستند که پس از ساده شدن مقادیر عددی یکسانی بهدست میدهند. چنین کسرهایی که به آنها کسرهای معادل هم گفته میشود، مقدار یا نسبت یکسانی را نشان میدهند. روشهای مختلفی برای تشخیص تساوی کسرها و بهدست آوردن کسرهای معادل وجود دارد که در این آموزش همراه با مثال آنها را توضیح دادیم.
در این مطلب سعی کردیم نکات و روشهای کاربردی مربوط به تساوی کسرها را بیان کنیم. پیشنهاد میکنیم پس از مطالعه این مقاله، به حل تمرینهای بیشتری بپردازید و از تمام روشهایی که نام بردیم در حل تمرینها استفاده کنید.