آموزش کامل جمع و تفریق کسرها | نحوه محاسبه + نمونه سوال

در آموزش‌های قبل با نحوه محاسبه ضرب و تقسیم کسرها آشنا شدیم. در این مقاله، قصد داریم به آموزش جمع و تفریق کسرها بپردازیم. عمل جمع و تفریق در کسرها براساس قوانین مشابهی انجام می‌شود که در آن قبل از هر چیز، باید مخرج‌ها مورد بررسی قرار گیرند.

اگر مخرج‌ها مساوی باشند، عمل جمع و تفریق به‌راحتی انجام می‌شود، اما اگر مخرج‌ها مساوی نباشند، با روشی که در این مقاله معرفی می‌کنیم، می‌توان کسرها را با هم جمع یا از هم کم کرد. در ادامه، با حل نمونه سؤال‌های متعدد در این مورد بیشتر توضیح خواهیم داد.

روش های جمع و تفریق کسرها

جمع و تفریق کسرها با مخرج مساوی

هنگام تفریق یا جمع کسرها، اولین چیزی که باید به آن توجه کرد، مخرج کسرها است. در واقع، قبل از هر چیز باید مطمئن شویم مخرج‌ها مساوی هستند یا نه. اگر مخرج‌ها مساوی باشند، کار ما راحت خواهد بود زیرا دیگر نیازی نیست مخرج‌ها را برابر کنیم. برای جمع کردن یا کم کردن کسرهایی که مخرج مساوی دارند، مطابق مراحل زیر پیش می‌رویم:

• مخرج کسر را ثابت و بدون تغییر نگه می‌داریم.
• صورت‌ها را با توجه به علامت جمع یا تفریق کسرها، با هم جمع یا از هم کم می‌کنیم.

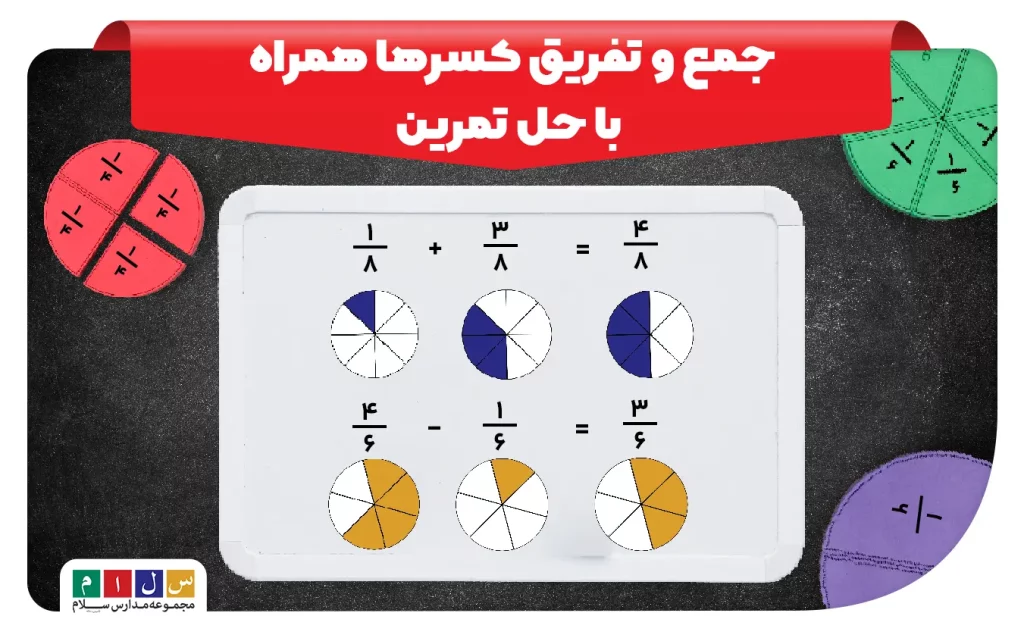
در  تصویر زیر، مثالی حل‌شده از جمع و تفریق کسرها آورده شده است. همان‌طور که می‌بینید، فرآیند عمل جمع و تفریق در کسرها تفاوت چندانی با یکدیگر ندارند؛ تنها تفاوت آن‌ها جمع یا کم کردن صورت‌ها است.

جمع و تفریق کسرها با مخرج نامساوی

اگر کسرهایی که می‌خواهیم عملیات جمع و تفریق روی آن‌ها انجام دهیم، دارای مخرج نامساوی باشند، ابتدا با مخرج مشترک گرفتن، مخرج‌ها را مساوی می‌کنیم، سپس عمل جمع یا تفریق را انجام می‌دهیم. برای مخرج مشترک گرفتن باید کوچک‌ترین مضرب مشترک مخرج‌ها را بیابیم. به مثال زیر دقت کنید.

می‌خواهیم حاصل تفریق را به‌دست آوریم. می‌بینیم که مخرج‌ها یکسان نیستند. برای اینکه مخرج‌ها برابر شوند، از کوچک‌ترین مضرب مشترک آن‌ها استفاده می‌کنیم. برای یافتن کوچک‌ترین مضرب مشترک، مضرب‌های هر کدام از اعداد مخرج را جداگانه مانند تصویر زیر یادداشت می‌کنیم.

همان‌طور که می‌بینید، اولین و کوچک‌ترین مضرب مشترک عدد ۳ و ۴، ۱۲ است. بنابراین، باید مخرج و درنتیجه صورت هر دو کسر را در عددی ضرب کنیم که مخرج‌ها مساوی ۱۲ شوند. با این کار، کسرهایی با مخرج مساوی خواهیم داشت که برابر با کسرهای اولیه هستند. 

پس از این مراحل، حالا می‌توانیم به‌راحتی دو کسر را از هم کم کنیم. شکل بالا تمام مراحل تفریق کسرها را به‌خوبی نشان می‌دهد.

پیشنهاد مطالعه: آموزش تقسیم کسرها

نمونه سؤال جمع و تفریق کسرها با جواب

سؤال ۱: حاصل تفریق زیر را به‌دست آورید.

$$\frac{۵}{۶}-<!--\; -\; -->\frac{۷}{۹}$$

جواب: مخرج‌های این عبارت برابر نیستند و باید با گرفتن مخرج مشترک، مخرج‌ها را مساوی کنیم. کافی‌ست ابتدا کوچک‌ترین مضرب مشترک مخرج‌ها تعیین شود.

• مضرب‌های ۶: ۶، ۱۲، ۱۸، ۲۴ و غیره.
• مضرب‌های ۹: ۹، ۱۸، ۲۷ و غیره.

کوچک‌ترین مضرب مشترک ۶ و ۹ عدد ۱۸ است. بنابراین، برای مساوی شدن مخرج‌ها باید صورت و مخرج کسر اول را در ۳ و صورت و مخرج کسر دوم را در ۲ ضرب کنیم.

$$\frac{۵}{۶}-<!--\; -\; -->\frac{۷}{۹}=\frac{۵\times <!--\; \times \; -->۳}{۶\times <!--\; \times \; -->۳}-<!--\; -\; -->\frac{۷\times <!--\; \times \; -->۲}{۹\times <!--\; \times \; -->۲}=\frac{۱۵}{۱۸}-<!--\; -\; -->\frac{۱۴}{۱۸}=\frac{۱۵-<!--\; -\; -->۱۴}{۱۸}=\frac{۱}{۱۸}$$

سؤال ۲: حاصل عبارت زیر را تعیین کنید.

$$۳\frac{۱}{۲}-<!--\; -\; -->۱\frac{۲}{۳}$$

جواب: در عبارت داده‌شده، عدد مخلوط وجود دارد که برای محاسبه حاصل تفریقشان ابتدا باید به‌صورت زیر به کسر تبدیل شوند:

$$۳\frac{۱}{۲}=\frac{۳\times <!--\; \times \; -->۲+۱}{۲}=\frac{۷}{۲}$$ $$۱\frac{۲}{۳}=\frac{۱\times <!--\; \times \; -->۳+۲}{۳}=\frac{۵}{۳}$$

اکنون دو کسر با مخرج نامساوی داریم که با یافتن کوچک‌ترین مضرب مشترکشان به‌راحتی می‌توان آن‌ها را مساوی کرد.

•  مضرب‌های ۲: ۲، ۴، ۶، ۸ و غیره.
• مضرب‌های ۳: ۳، ۶، ۹ و غیره.

کوچک‌ترین مضرب مشترک ۲ و ۳ عدد ۶ است. بنابراین، باید کاری کنیم که مخرج‌های مساوی با ۶ شوند.

$$۳\frac{۱}{۲}-<!--\; -\; -->۱\frac{۲}{۳}=\frac{۷}{۲}-<!--\; -\; -->\frac{۵}{۳}=\frac{۷\times <!--\; \times \; -->۳}{۲\times <!--\; \times \; -->۳}-<!--\; -\; -->\frac{۵\times <!--\; \times \; -->۲}{۳\times <!--\; \times \; -->۲}=\frac{۲۱}{۶}-<!--\; -\; -->\frac{۱۰}{۶}=\frac{۲۱-<!--\; -\; -->۱۰}{۶}=\frac{۱۱}{۶}$$

جواب به‌دست‌آمده یک کسر بزرگ‌تر از واحد است که می‌توان از قواعد تبدیل کسر را به عدد مخلوط استفاده کرد.

$$۳\frac{۱}{۲}-<!--\; -\; -->۱\frac{۲}{۳}=\frac{۱۱}{۶}=\frac{۶+۵}{۶}=\frac{۶}{۶}+\frac{۵}{۶}=۱+\frac{۵}{۶}=۱\frac{۵}{۶}$$

سؤال ۳: مقدار عبارت‌های زیر را محاسبه کنید.

الف )

$$۵\frac{۲}{۷}+۳\frac{۴}{۷}-<!--\; -\; -->۴\frac{۵}{۷}$$

ب)

$$۴\frac{۲}{۳}+۲\frac{۴}{۵}-<!--\; -\; -->۱\frac{۵}{۶}$$

الف) برای به‌دست آوردن پاسخ این عبارت، اول از همه اعداد مخلوط را به کسر تبدیل می‌کنیم:

$$۵\frac{۲}{۷}=\frac{۵\times <!--\; \times \; -->۷+۲}{۷}=\frac{۳۷}{۷}$$ $$۵\frac{۲}{۷}=\frac{۵\times <!--\; \times \; -->۷+۲}{۷}=\frac{۳۷}{۷}$$ $$۴\frac{۵}{۷}=\frac{۴\times <!--\; \times \; -->۷+۵}{۷}=\frac{۳۳}{۷}$$

همان‌طور که می‌بینید، مخرج هر سه کسر یکسان است و دیگر نیازی به مخرج مشترک گرفتن نداریم. خواهیم داشت:

$$۵\frac{۲}{۷}+۳\frac{۴}{۷}-<!--\; -\; -->۴\frac{۵}{۷}=\frac{۳۷}{۷}+\frac{۲۵}{۷}-<!--\; -\; -->\frac{۳۳}{۷}=\frac{۳۷+۲۵-<!--\; -\; -->۳۳}{۷}=\frac{۶۲-<!--\; -\; -->۳۳}{۷}=\frac{۲۹}{۷}$$

کسر حاصل را به عدد مخلوط تبدیل می‌کنیم:

$$\frac{۲۹}{۷}=\frac{۲۸+۱}{۷}=\frac{۲۸}{۷}+\frac{۱}{۷}=۴+\frac{۱}{۷}=۴\frac{۱}{۷}$$

ب) ابتدا اعداد مخلوط را به‌صورت کسر می‌نویسیم:

$$۴\frac{۲}{۳}=\frac{۴\times <!--\; \times \; -->۳+۲}{۳}=\frac{۱۴}{۳}$$ $$۲\frac{۴}{۵}=\frac{۲\times <!--\; \times \; -->۵+۴}{۵}=\frac{۱۴}{۵}$$ $$۱\frac{۵}{۶}=\frac{۱\times <!--\; \times \; -->۶+۵}{۶}=\frac{۱۱}{۶}$$

درنتیجه

$$۴\frac{۲}{۳}+۲\frac{۴}{۵}-<!--\; -\; -->۱\frac{۵}{۶}=\frac{۱۴}{۳}+\frac{۱۴}{۱۵}-<!--\; -\; -->\frac{۱۱}{۶}$$

مخرج کسرها نامساوی است و باید برای یکسان کردن آن‌ها مخرج مشترک گرفت. این کار را با پیدا کردن کوچک‌ترین مضرب مشترک اعداد مخرج انجام می‌دهیم.

• مضرب‌های ۳: ۳، ۶، ۹، ۱۲، ۱۵، ۱۸، ۲۱، ۲۴، ۲۷، ۳۰ و غیره.
• مضرب‌های ۵: ۵، ۱۰، ۱۵، ۲۰، ۲۵، ۳۰ و غیره.
• مضرب‌های ۶: ۶، ۱۲، ۱۸، ۲۴، ۳۰، ۳۶ و غیره.

کوچک‌ترین مضرب مشترک این سه عدد ۳۰ است. بنابراین، مخرج مشترک این سه کسر را عدد ۳۰ قرار می‌دهیم.

$$\frac{۱۴}{۳}+\frac{۱۴}{۵}-<!--\; -\; -->\frac{۱۱}{۶}=\frac{۱۴\times <!--\; \times \; -->۱۰}{۳\times <!--\; \times \; -->۱۰}+\frac{۱۴\times <!--\; \times \; -->۶}{۵\times <!--\; \times \; -->۶}=\frac{۱۴۰}{۳۰}+\frac{۸۴}{۳۰}-<!--\; -\; -->\frac{۵۵}{۳۰}=\frac{۱۴۰+۸۴-<!--\; -\; -->۵۵}{۳۰}=\frac{۱۶۹}{۳۰}$$

کسر بزرگ‌تر از واحد را می‌توانیم به عدد مخلوط تبدیل کنیم:

$$\frac{۱۶۹}{۳۰}=\frac{۱۵۰+۱۹}{۳۰}=\frac{۱۵۰}{۳۰}+\frac{۱۹}{۳۰}=۵+\frac{۱۹}{۲۰}=۵\frac{۱۹}{۳۰}$$

سخن پایانی

جمع و تفریق کسرها ازجمله مهارت‌های پایه‌ای برای انجام محاسبات مربوط به کسرها است که از قوانین مشابهی پیروی می‌کنند. به‌طور کلی، هنگام جمع یا کم کردن کسرها لازم است مخرج آن‌ها با هم مساوی باشد. اگر مخرج‌ها مساوی نباشند، با استفاده از کوچک‌ترین مضرب مشترکشان، آن‌ها را با هم برابر می‌کنیم.

برای اینکه تسلط بیشتری بر مطالب گفته‌شده در این مقاله داشته باشید، توصیه ما این است که مثال‌ها و تمرین‌های بیشتری از جمع و تفریق کسرها بدون مخرج مشترک گرفتن (مخرج‌های مساوی) و با مخرج مشترک گرفتن (مخرج‌های نامساوی) حل کنید.