آموزش تفریق اعداد مخلوط به زبان ساده+ شکل و محور

با توجه به اینکه اعداد مخلوط شامل دو بخش صحیح و کسری هستند، شاید در نگاه اول تفریق کردن آن‌‌ها از یکدیگر چالش‌‌برانگیز به نظر برسد، اما این تصوری بیش نیست چرا که با انجام چند تبدیل ساده می‌‌توانید به‌‌راحتی این اعداد را از هم کم کنید. در آموزش‌های قبل درباره جمع و تفریق اعداد مخلوط به صورت کوتاه صحبت کردیم. در این آموزش‌‌، روش‌‌هایی را به شما خواهیم آموخت که با به‌‌کار بردن آن‌‌ها بتوانید تفریق اعداد مخلوط را به‌‌راحتی انجام دهید. پس تا انتها این مطلب را دنبال کنید.

عدد مخلوط چیست؟

پیش از اینکه روش‌‌های تفریق اعداد مخلوط را آموزش دهیم، خوب است با تعریفی کوتاه یادآوری کنیم که این دسته از اعداد چه هستند و چگونه نمایش داده می‌‌شوند.
عدد مخلوط به عددی گفته می‌‌شود که از دو بخش عدد صحیح (یا کامل) و عدد کسری تشکیل شده است و برای نشان دادن کسر بزرگ‌‌تر از واحد مورد استفاده قرار می‌‌گیرد. برای مثال، اگر بخواهیم کسر را که مقدار صورت از مخرجش بیشتر است به‌‌صورت عدد مخلوط نمایش دهیم، آن را به این صورت می‌‌نویسیم: عدد ۳ بخش صحیح و کسر ۱۴ بخش کسری این عدد مخلوط را تشکیل می‌‌دهد.

تفریق اعداد مخلوط با شکل

با توجه به اینکه استفاده از شکل، درک بصری مفاهیم ریاضی را بالا می‌‌برد، ابتدا روش انجام تفریق اعداد مخلوط را با رسم شکل توضیح می‌‌دهیم. فرض کنید قرار است حاصل تفریق زیر را تعیین کنیم:

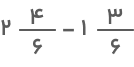
برای حل چنین عبارتی، ابتدا شکل مربوط به اولین عدد مخلوط یعنی را رسم می‌‌کنیم. این عدد نشان می‌‌دهد که ۲ واحد و ۴ قسمت از ۶ قسمت یک واحد کامل را داریم. بنابراین نخست باید ۲ واحد کامل که به ۶ قسمت مساوی تقسیم شده است و یک واحد کامل را مانند آنچه در تصویر زیر می‌‌بینید رسم کنیم.
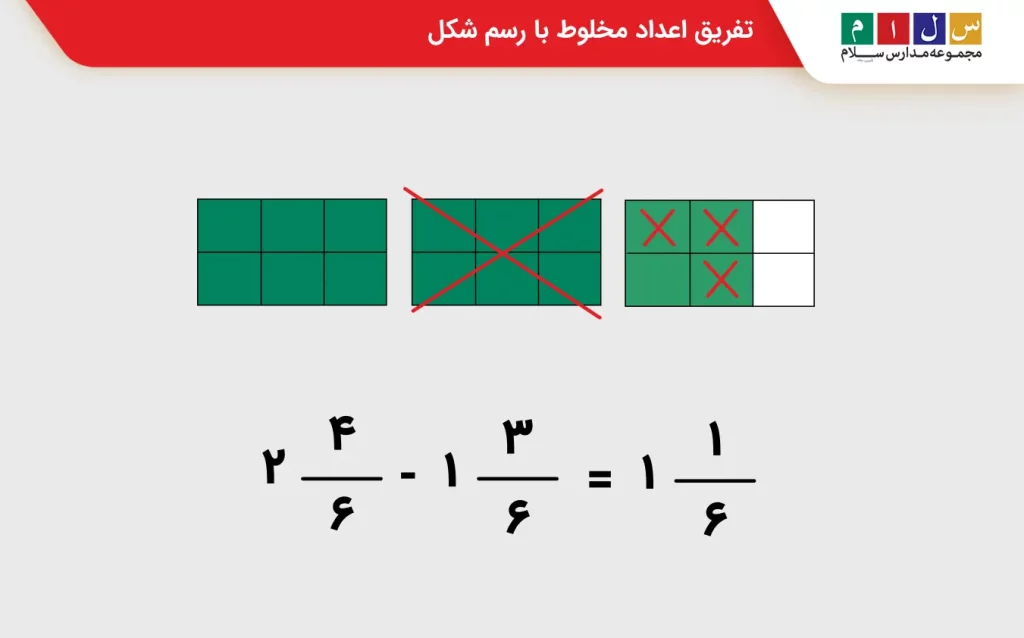
اکنون نوبت به کم کردن عدد دوم یعنی ۱۳۶ از عدد اول می‌‌رسد. در این مرحله کافی‌‌ست به‌‌اندازه ۱ واحد و یک واحد کامل از شکل رسم‌‌شده را مطابق تصویر زیر با علامت × حذف کنیم. آنچه از شکل باقی می‌‌ماند ۱ واحد و یک واحد کامل است که حاصل تفریق را به ما نشان خواهد داد.

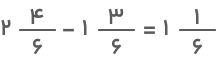
تفریق اعداد مخلوط روی محور

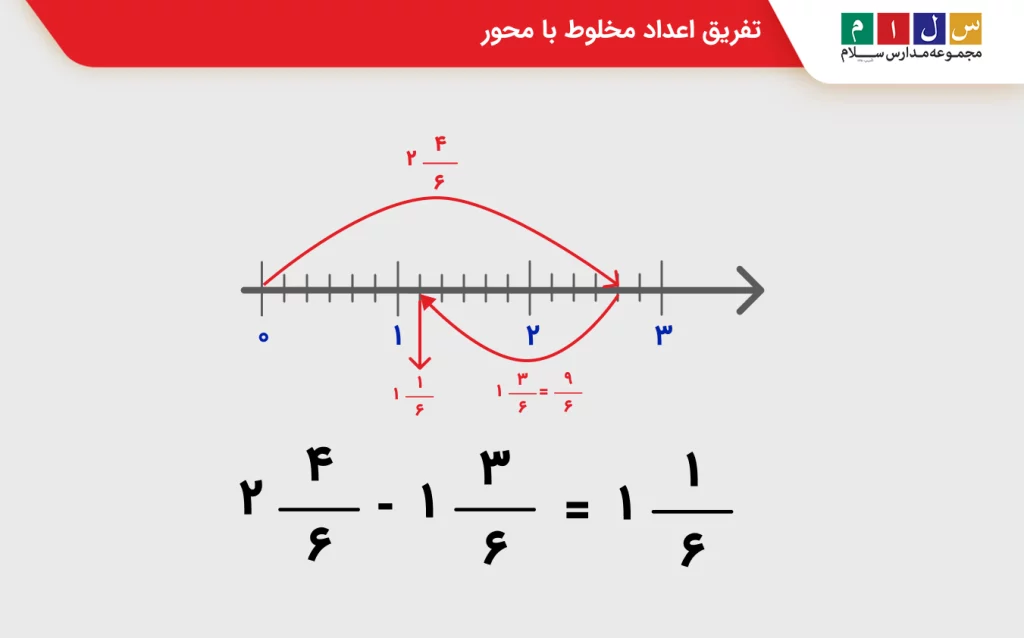
رسم محور نیز یک روش بصری دیگر برای به‌‌دست آوردن حاصل تفریق اعداد مخلوط است. فرض کنید می‌‌خواهیم مثال بخش قبلی را این بار با کمک محور اعداد حل کنیم:

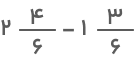
با توجه به مساوی بودن مخرج هر دو عدد، استفاده از محور اعداد بسیار راحت خواهد بود. چون مخرج برابر با ۶ است، بایستی هر واحد محور را به ۶ قسمت مساوی تقسیم کنیم. پس از تقسیم‌‌بندی، به‌‌اندازه عدد اول یعنی ۲ واحد و جدا کرده و با کمک کمان نشان می‌‌دهیم. حالا برای اینکه عدد دوم را از عدد اول کم کنیم لازم است یک کمان از انتهای کمان اول رسم کرده و ۱ واحد و به عقب برویم. انتهای کمان دوم پاسخ تفریق را نشان خواهد داد.
توجه داشته باشید که برای راحتی در انجام عمل تفریق می‌‌توانید عدد مخلوط دوم را ابتدا به کسر تبدیل کنید و سپس روی محور آن را نشان دهید.

تفریق اعداد مخلوط به روش محاسبه

تا اینجا با روش‌‌های بصری محاسبه تفریق اعداد مخلوط آشنا شدیم. در این بخش، حالت‌‌ها و روش‌‌های مختلف کم کردن عدد مخلوط، کوچکتر از بزرگتر و عدد مخلوط از عدد صحیح و عدد کسری را به روش محاسبه شرح خواهیم داد.

تفریق اعداد مخلوط با مخرج مساوی

اگر دو عدد مخلوطی که می‌‌خواهیم آن‌‌ها را از هم کم کنیم، مخرج یکسانی داشته باشند، می‌‌توانیم از دو روش استفاده کنیم. عبارت زیر را در نظر بگیرید. می‌‌خواهیم با کمک دو روش زیر حاصل آن را به‌‌دست آوریم.

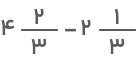
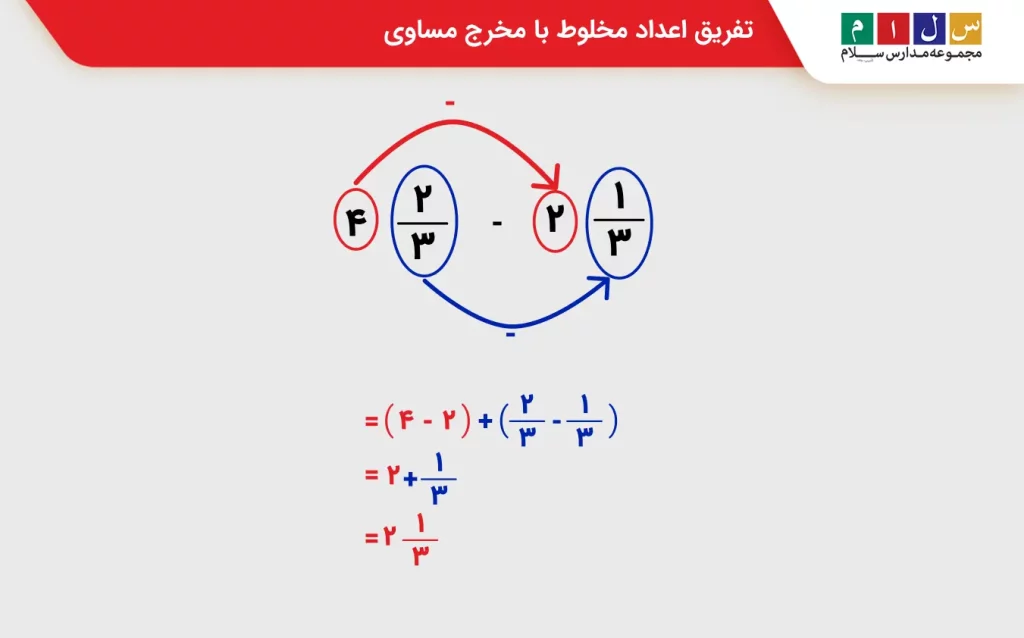
• روش اول: می‌‌دانیم که عدد مخلوط را می‌‌توانیم به‌‌صورت حاصل‌‌جمع یک عدد صحیح و یک عدد کسری بنویسیم. با این توضیح می‌‌توان عبارت بالا را به‌‌شکل زیر بازنویسی کرد:

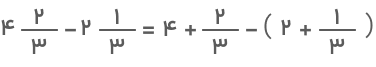
اکنون کافی‌‌ست دو عدد صحیح و دو عدد کسری را جداگانه از هم کم کنیم تا حاصل تفریق به‌‌دست آید:

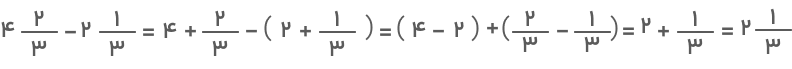
• روش دوم: روش دیگری نیز برای محاسبه تفریق عدد مخلوط با مخرج مساوی وجود دارد. در این روش از تبدیل عدد مخلوط به کسر کمک می‌‌گیریم. به این صورت که ابتدا هر یک از اعداد مخلوط را به کسر تبدیل کرده و سپس آن‌‌ها را از هم کم می‌‌کنیم. اگر مثال قبل را با همین روش حل کنیم، پاسخ ما به‌‌صورت زیر به‌‌دست خواهد آمد:

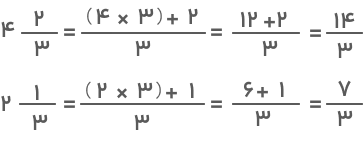
درنتیجه

حاصل عبارت به‌‌صورت یک کسر بزرگ‌‌تر از واحد است. برای اینکه جواب به‌‌دست‌‌آمده را به‌‌شکل عدد مخلوط بنویسیم از روش‌‌های تبدیل کسر به عدد مخلوط استفاده می‌‌کنیم. خواهیم دید که پاسخ همان خواهد بود که در روش اول به‌‌دست آمد.

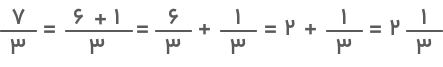
پیشنهاد مطالعه: آموزش تبدیل کسر به عدد مخلوط

تفریق اعداد مخلوط با مخرج نامساوی

در این بخش حالتی را بررسی می‌‌کنیم که دو عدد مخلوط مخرج نامساوی دارند. روش‌‌هایی که برای حالت مساوی بودن مخرج‌‌ها توضیح دادیم در حالت نامساوی بودن آن‌‌ها نیز قابل استفاده خواهند بود. در اینجا نیز برای هر کدام از روش‌‌ها به حل مثال می‌‌پردازیم.

به‌‌عنوان مثال، فرض کنید قرار است حاصل عبارت زیر را با دو راه‌‌حل مختلف به‌‌دست آوریم:

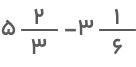
• روش اول: در روش اول، اعداد صحیح را به‌‌صورت جدا و اعداد کسری را جداگانه از هم کم می‌‌کنیم:

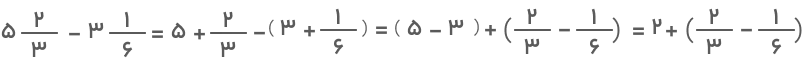
در این مثال به‌‌دلیل اینکه مخرج‌‌ها برابر نیستند، باید با استفاده از روش‌‌های مخرج مشترک گرفتن مخرج کسرها را برابر کنیم و سپس عمل تفریق را انجام دهیم.

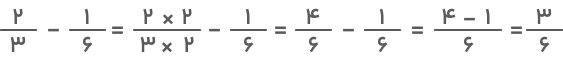
پس از ساده‌‌سازی خواهیم داشت:

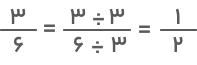
درنهایت، حاصل عبارت به‌‌صورت زیر خواهد بود:

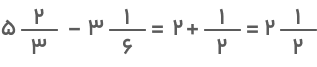
• روش دوم: شیوه دیگری که برای انجام تفریق اعداد مخلوط با مخرج نامساوی وجود دارد این است که اول دو عدد مخلوط را به کسر تبدیل کنیم. در این صورت عبارت روش اول را می‌‌توانیم به‌‌صورت زیر بنویسیم:

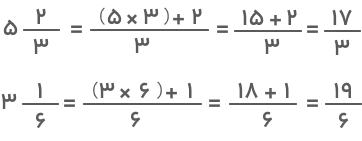
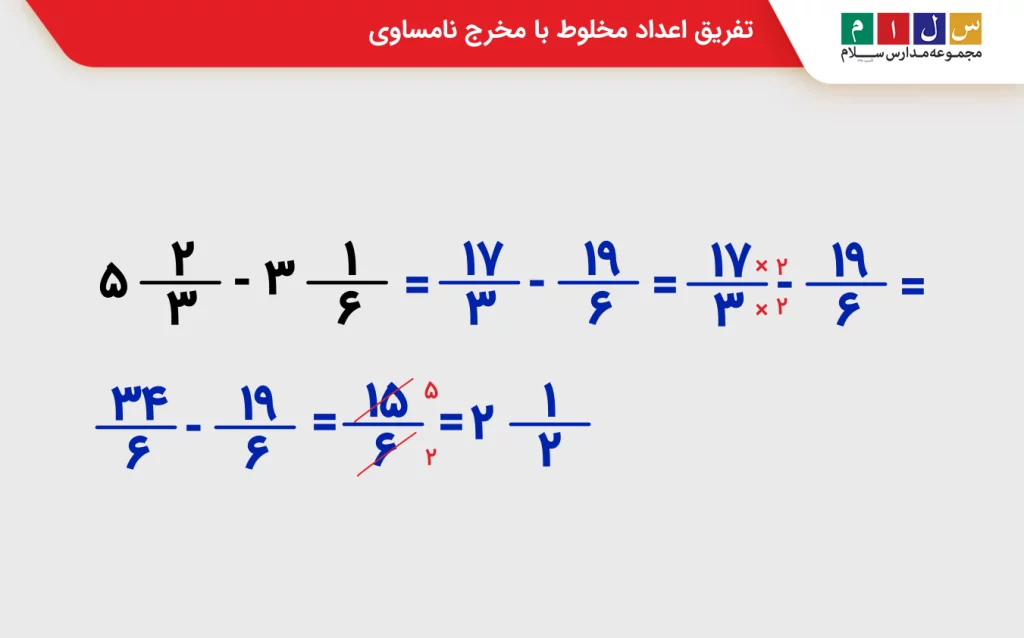
برای رسیدن به جواب نهایی باید اول مخرج مشترک بگیریم، سپس کسرها را از هم کم کنیم:

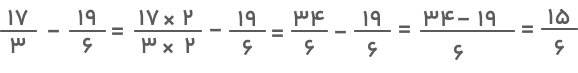
کسر حاصل را می‌‌توان ساده‌‌تر کرد:

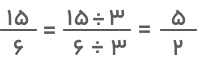
پاسخ به‌‌دست‌‌آمده را به‌‌شکل عدد مخلوط می‌‌نویسیم:

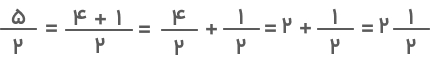
همان‌‌طور که می‌‌بینید، جواب حاصل در این روش مشابه روش قبلی است.

پیشنهاد مطالعه: چگونه مخرج مشترک بگیریم؟

تفریق عدد صحیح از عدد مخلوط

در این حالت، تنها کاری که لازم است انجام دهید، کم کردن اعداد صحیح از یکدیگر است. بنابراین، دیگر نیازی نیست که بخش‌‌های کسری را از هم کم کنید. مثال‌‌های زیر گویای این موضوع هستند:

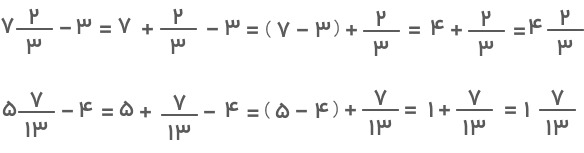
تفریق عدد مخلوط از عدد صحیح

در این حالت، تفریق را با دو روش می‌‌توان انجام داد:

• روش اول: در این روش، عدد مخلوط را به کسر تبدیل کرده و به عدد صحیح نیز مخرج یک می‌‌دهیم تا به‌‌شکل کسر درآید. با این کار، دو کسر خواهیم داشت که عمل تفریق آن‌‌ها به‌‌سادگی قابل انجام است. برای فهم بهتر به مثال زیر توجه کنید:

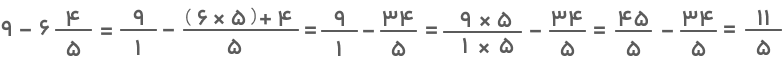
کسر حاصل را به عدد مخلوط تبدیل می‌‌کنیم:

• روش دوم: روش دیگری که می‌‌توان به‌‌کار برد، نوشتن عدد صحیح به‌‌شکل عدد مخلوط است. این روش را با یک مثال توضیح می‌‌دهیم. فرض کنید می‌‌خواهیم تفریق را انجام دهیم. برای این کار ابتدا به مخرج کسر عدد مخلوط نگاه کرده و هر واحد کامل را به همان اندازه به قسمت‌‌های مساوی تقسیم می‌‌کنیم. با توجه به اینکه در این مثال مخرج ۷ است، عدد صحیح ۴ را می‌‌توان به‌‌شکل زیر گسترده کرد:

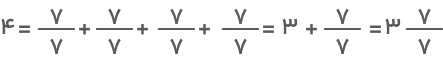
اکنون می‌‌توانیم تفریق دو عدد را طبق روش‌‌هایی که در این مقاله بیان کردیم به‌‌راحتی انجام دهیم:

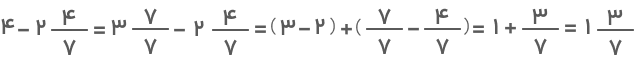
تفریق عدد مخلوط و عدد کسری

انجام تفریق عدد کسری و عدد مخلوط بسیار ساده است. برای این کار کافی‌‌ست عدد مخلوط را به کسر تبدیل کرده و سپس دو کسر را از هم کم کنید. مثال زیر این مراحل را به‌‌خوبی نشان می‌‌دهد.

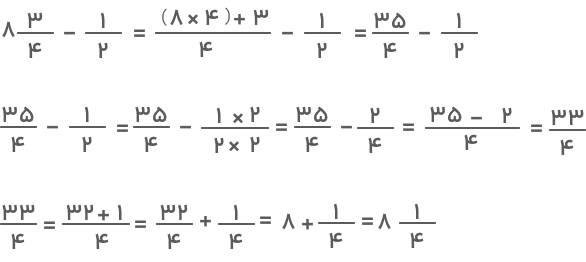
نمونه سؤال های تفریق عدد مخلوط با جواب

جواب عبارت‌‌های زیر را به‌‌دست آورید.

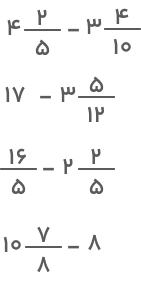
جواب: عبارت‌‌های داده‌‌شده را با کمک روش‌‌های ارائه‌‌شده حل می‌‌کنیم. شما نیز می‌‌توانید این عبارت‌‌ها را حل کرده و پاسخ خودتان را با جوابی که در اینجا می‌‌بینید مقایسه کنید تا صحت پاسخ خود را بیابید. جواب این عبارت‌‌ها به شرح زیر است:

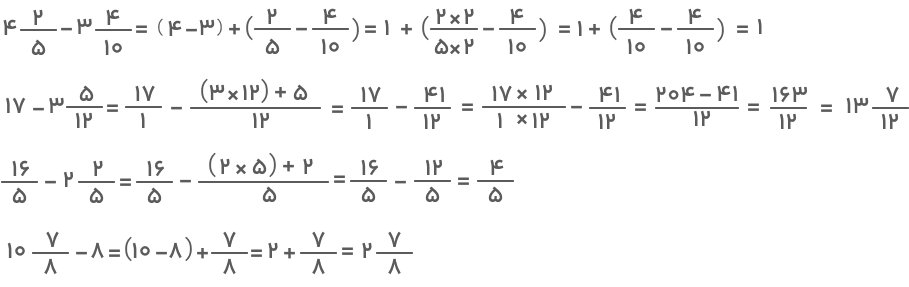
سخن پایانی

در این مطلب سعی کردیم تمام روش‌‌های موجود برای انجام تفریق اعداد مخلوط را توضیح دهیم. این روش‌‌ها بسته به اینکه مخرج کسرها مساوی یا نامساوی باشند یا عدد اول و دوم عبارت، یک عدد صحیح یا کسری باشد با هم متفاوت بودند که با ذکر مثال برای هر یک، شیوه انجام آن‌‌ها را آموختیم. همان‌‌طور که دیدید تمام این روش‌‌ها بسیار ساده هستند و تنها راه تسلط بر آن‌‌ها حل مسائل متعدد و کاربردی است.