فهرست مطالب
Toggleگاهی در ریاضیات با مسائلی روبهرو میشویم که به ظاهر پیچیده و طولانی به نظر میرسند، اما با یک فرمول ساده میتوان آنها را به سرعت حل کرد. اتحاد چاق و لاغر یکی از این روش ها است که با آن مجموع یا تفاضل مکعب دو جمله را به شکل ضربی ساده تبدیل کنیم. درک این اتحاد محاسبات را سریعتر میکند و در حل معادلات و تجزیه عبارتهای جبری، دست شما را باز میگذارد. اتحاد چاق و لاغر همچنین یکی از دروس مهم در ریاضیات متوسطه محسوب میشود و دانشآموزان باید بر آن تسلط داشته باشند.
از این رو در ادامه این مطلب از مجموعه مدارس سلام به آموزش اتحاد چاق و لاغر با مثال و توضیحات ساده میپردازیم. با شناخت دقیق این اتحاد، خواهید دید که بسیاری از عبارتهای به ظاهر دشوار، چقدر راحت قابل سادهسازی هستند. در مطلبی دیگر درباره اتحاد جمله مشترک صحبت کردهایم پس از خواندن آن غافل نشوید.
اتحاد چاق و لاغر چیست؟
اتحاد چاق و لاغر یک اتحاد جبری برای مجموع و تفاضل مکعب دو جمله است و به شکل زیر نوشته میشود:
a³+ b³ = ( a + b) (a²- ab + b²)
a³- b³ = ( a – b) (a²+ ab + b²)
در این فرمولها، پرانتزی که جمع دو جمله را در بر دارد به «لاغر» و پرانتزی ترکیبی که شامل تفاضل و جمله میانی است به «چاق» معروف است. استفاده از این اتحاد برای این بوده که بتوانید معادلات درجه سوم و عبارتهای جبری طولانی را سریع و ساده حل کنید. توجه داشته باشید که این فرمول با اتحاد تفاضل دو مربع متفاوت است و نباید با آن اشتباه گرفته شود.
اتحاد چاق و لاغر مجموع مکعبات به این صورت است که هر دو علامت اول مثبت و علامت پرانتز چاق مشابه تصویر منفی است:

اتحاد چاق و لاغر تفاضل مکعبات به این صورت است که هر دو علامت اول منفی و علامت پرانتز چاق مشابه تصویر مثبت است:

نکته: نام دیگر اتحاد چاق و لاغر، اتحاد فیل و فنجان است!
پیشنهاد مطالعه: اتحاد مکعب چیست؟
چرا به آن اتحاد چاق و لاغر میگویند؟
نامگذاری این اتحاد و فرمول ریاضی کمی عجیب به نظر میرسد و همین باعث میشود دانشآموزان بخواهند بدانند چرا چنین نامی دارد. تنها دلیل این نامگذاری، ظاهر این اتحاد است! در ظاهر، این اتحاد در یک پرانتز کوچک و یک پرانتز بزرگ قرار میگیرد که پرانتز کوچک لاغر و بزرگ هم چاق است.
- بخش لاغر: (a+b)
- بخش چاق: (a²- ab + b²)(a + b)

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
آموزش اتحاد چاق و لاغر
آموزش اتحاد چاق و لاغر ریاضی به این شرح است:
- مجموع دو مکعب:
اگر دو عدد a و b داشته باشیم، مجموع مکعب آنها را میتوان به صورت ضربی نوشت:
a³+ b³ = ( a + b)(a²- ab + b²)
در این فرمول، پرانتز اول جمع دو عدد است و پرانتز دوم ترکیبی از مربع هر عدد و حاصل ضرب آنهاست. با این روش، به جای محاسبه جداگانه توان سوم و سپس جمع، میتوانیم مستقیماً به یک ضرب ساده برسیم. این تکنیک به ویژه در حل معادلات و سادهسازی عبارتهای جبری طولانی کاربرد فراوان دارد.
- تفاضل دو مکعب:
برای تفاضل دو مکعب داریم:
a³- b³ = (a – b)(a²+ ab + b²)
در این حالت، پرانتز اول تفاضل ساده دو عدد است و پرانتز دوم شامل مربعهای آنها و حاصل ضربشان، اما با همه علامتها مثبت است. این ساختار باعث میشود که تفاضل مکعبها هم به راحتی فاکتورگیری و ساده شود.
پیشنهاد مطالعه: اتحاد مزدوج چیست؟
اثبات اتحاد چاق و لاغر
اثبات اتحاد چاق و لاغر هم برای حالت تفاضل است و هم برای مجموع. در این قسمت برای یادگیری بهتر و آسانتر، هر یک را جداگانه بررسی کردهایم.
اثبات اتحاد چاق و لاغر تفاضل
برای اثبات اتحاد چاق و لاغر در تفاضل، باید این تساوی را ثابت کنیم:
(a-b)(a²+ab+b²) = a³-b³
در ابتدا میتوانیم قسمت سمت چپ تساوی را بر اساس خاصیت بخشپذیری بنویسیم:
( a²+ab+ b2)(b)-( a²+ab+ b2)(a)
سپس همانطور که مشخص است، میتوانیم a را در پرانتز اول و b را در پرانتز دوم ضرب کنیم که حاصل به این ترتیب میشود:
(a²b+ab²+b³)-(a³+a²b+ab²)
در مرحله بعد، جملات مشابه را کنار یکدیگر میچینیم:
a³+ab²+ba²-ba²-ab²-b³
حالا قرینهها را از جملات حذف میکنیم که ترتیب زیر باقی میماند و اثبات اتحاد چاق و لاغر انجام میشود:
a³-b³
اثبات اتحاد چاق و لاغر مجموع
برای اثبات اتحاد چاق و لاغر در مجموع، باید این تساوی را ثابت کنیم:
(a+b)(a²-ab+b²) = a³+b³
در ابتدا میتوانیم قسمت سمت چپ تساوی را بر اساس خاصیت بخشپذیری بنویسیم:
(a²-ab+b²)(b)+(a²-ab+b²)(a)
سپس همانطور که مشخص است، میتوانیم a را در پرانتز اول و b را در پرانتز دوم ضرب کنیم که حاصل به این ترتیب میشود:
(a²b-ab²+b³)+(a³-a²b+ab²)
در مرحله بعد، جملات مشابه را کنار یکدیگر میچینیم:
a³-a²b+a²b+ab²-ab²+b³
حالا قرینهها را از جملات حذف میکنیم که ترتیب زیر باقی میماند و اثبات اتحاد چاق و لاغر انجام میشود:
a³+b³
پیشنهاد مطالعه: آموزش جمع و تفریق ذهنی
تعبیر هندسی اتحاد چاق و لاغر
اگر بخواهیم برای اتحاد چاق و لاغر دهم تجربی تعبیر هندسی بنویسیم، بررسی تفاضل و مجموع بهصورت جداگانه به درک بهتر این تعبیر کمک میکند. در این قسمت به این تعبیر هندسی اتحاد چاق و لاغر پرداختهایم.
تعبیر هندسی تفاضل
فرض کنید دو مکعب با ضلعهای x و y داریم که به ترتیب حجم آنها برابر با x³ و y³ است.
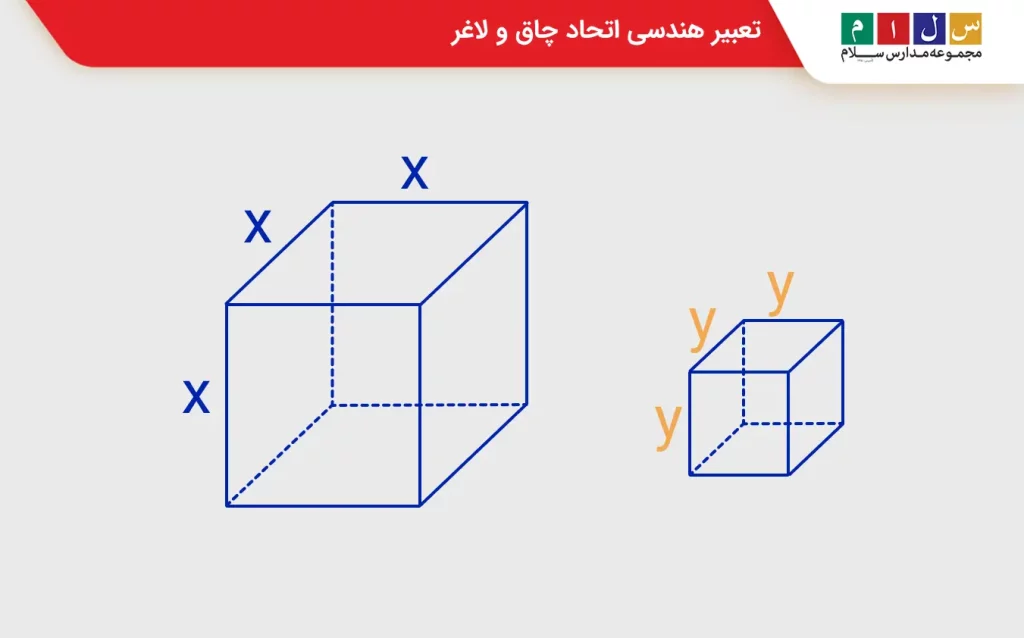
اگر بخواهیم تفاضل این دو حجم را نشان بدهیم، میتوانیم مکعب بزرگتر را به چند بخش کوچکتر تقسیم کنیم. این تقسیمبندی باعث میشود که بتوانیم حجم x³ را به صورت مجموع چهار بخش مستقل بنویسیم:
x³ = y³ + x²(x-y) + xy(x-y) + y²(x-y)

با حذف بخش مشترک y³ از دو طرف، خواهیم داشت:
x³ – y³ = x²(x-y) + xy(x-y) + y²(x-y)
و در نهایت، اگر عامل مشترک (x-y) را بیرون بکشیم، به اتحاد زیر میرسیم:
x³ – y³ = (x-y)(x²+xy+y²)
تعبیر هندسی مجموع
برای مجموع دو مکعب با ضلعهای a و b، ابتدا دو مکعب جدا با حجمهای a³ و b³ در نظر میگیریم.

حال اگر مکعب کوچکتر را روی مکعب بزرگتر قرار بدهیم و خطوط فرضی را رسم کنیم، میتوانیم یک مکعب مستطیل بزرگتر را تصور کنیم:

ابعاد آن برابر است با:
V = a × a × (a+b) = a²(a+b)
اما این مکعب مستطیل شامل بخشهای اضافهای است که وجود خارجی ندارند.به این ترتیب قسمت فرضی را دو قسمت میکنیم و مجموع دو مکعب اصلی تفاضل میکنیم.

اگر حجم این بخشهای اضافی را محاسبه کرده و از کل کم کنیم تا تجزیه اتحاد چاق لاغر انجام شود، حجم واقعی دو مکعب a³+b³ به دست میآید. حجم بخشهای فرضی به این ترتیب است:
Va,b = a2 (a+b)-[ab(a-b)+b2(a-b)]
سپس میتوانیم (a-b)b را از درون براکت فاکتور گرفته تا در دو جمله یک عامل مشترک (a+b) باقی بماند. میتوانیم آنها را هم بهصورت مشترک فاکتور بگیریم و سادهسازی کنیم که نتیجه میشود:
Va,b = (a+b)(a2-ab+b2)
این نتیجه به دست آمده همان مجموع حجم دو مکعب است. محاسبات نشان میدهد:
a³+b³ = (a+b)(a²-ab+b²)

کاربردهای اتحاد چاق و لاغر
- سادهسازی روابط پیچیده ریاضی و سرعت بخشیدن به محاسبات عددی
- استفاده در تحلیل نیروها، حرکت و طراحی سازهها در مهندسی و فیزیک
- کمک به بهینهسازی الگوریتمها و کاهش پیچیدگی کد در برنامهنویسی
- کاربرد در گرافیک کامپیوتری و پردازش دادهها برای افزایش کارایی
- بهینهسازی محاسبات هوش مصنوعی و یادگیری ماشین
- پشتیبانی از طراحی مدلهای پیشبینی و شبکههای عصبی در علوم داده
مثال از اتحاد چاق و لاغر
- نمونه سوال اتحاد چاق و لاغر با جواب:
عبارت زیر را تجزیه کنید:
1−216x³y³
راهحل:
برای سادهتر شدن حل این عبارت باید بدانیم که میتوانیم آن را به این شکل بنویسیم:
216=(6)(6)(6)=6³
1 =(1)(1)(1)=1³
سپس میتوان نوشت:
1 − 216x³y³
= (1)³ − (6xy)³
= (1 − 6xy) [(1)² + (1)(6xy) + (6xy)²]
= (1 − 6xy)(1 + 6xy + 36x²y²)
- نمونه سوال اتحاد چاق و لاغر با جواب:
عبارت زیر را تجزیه کنید:
x⁶ − y⁶
راهحل:
برای این عبارت میتوانیم به شکل زیر حل معادله و تجزیه را انجام دهیم:
x⁶ − y⁶ = (x²)³ − (y²)³
سپس خواهیم داشت:
(x² − y²)((x²)² + (x²)(y²) + (y²)²)
عبارت پرانتز اول را باز میکنیم:
(x − y)(x + y)(x⁴ + x²y² + y⁴)
اکنون پرانتز سوم را بازنویسی میکنیم:
(x − y)(x + y)((x² + y²)² − x²y²)
و در نهایت به تجزیه کامل میرسیم:
(x − y)(x + y)(x² − xy + y²)(x² + xy + y²)
جمعبندی
اتحاد چاق و لاغر، با قدرت سادهسازی عبارات پیچیده و تجزیه مکعبها، ابزاری است که هم در کلاس درس و هم در حل مسائل واقعی کاربرد دارد. با تمرین و دقت در بهکارگیری آن، میتوان روابط جبری را سریعتر و دقیقتر تحلیل کرد و درک عمیقتری از ساختار ریاضی پیدا نمود.
سوالات متداول
- اتحاد چاق و لاغر ریاضی دهم چیست؟
این اتحاد یک اتحاد جبری به این شکل a³+ b³ = ( a + b)(a²- ab + b²) است. - نام دیگر اتحاد چاق و لاغر چیست؟
به آن اتحاد فیل و فنجان میگویند.









