همه ما هنگام دیدن برج‌ها، ساختمان‌ها و کوه‌ها و حتی رصد خورشید و ماه و سایر اجرام آسمانی و چیزهایی از این قبیل، نگاهمان را به‌سمت بالا می‌بریم تا بتوانیم بالاترین نقطه آن‌ها را مشاهده کنیم. در چنین مواردی که فاصله بلندترین نقطه از سطح زمین زیاد است، اولین چیزی که به ذهنمان می‌رسد این است که چیزی که دیده‌ایم چقدر بلند و مرتفع است. بلندی یا ارتفاع یک مفهوم هندسی پرکاربرد است که در این مقاله به آن خواهیم پرداخت. اگر شما نیز می‌خواهید بدانید ارتفاع چیست و در انواع اشکال هندسی چگونه آن را مشخص کنید، ادامه این مطلب را دنبال کنید.
مفهوم ارتفاع در ریاضی چیست؟
در ریاضی، ارتفاع به‌عنوان فاصله عمودی بالاترین نقطه جسم تا قاعده (پایینترین نقطه) آن تعریف میشود. درواقع، اصطلاح ارتفاع در هندسه به اندازه‌گیری یک جسم در امتداد یک محور عمودی اشاره دارد. برای اندازه‌گیری ارتفاع از ابزارها و واحدهای اندازه‌گیری طول استفاده میشود. برای مثال، برای اندازه‌گیری قد که فاصله بالاترین نقطه بدن یعنی سر تا پایینترین آن یعنی پا را نشان می‌دهد، معمولاً از واحد سانتی‌متر یا متر استفاده میشود.
شکل زیر را نگاه کنید. این شکل به‌خوبی مفهوم ارتفاع را نشان می‌دهد. در این تصویر، سه درخت با ارتفاع متفاوت دیده میشود و فاصله عمودی بالاترین نقطه هر یک از این درخت‌ها از سطح زمین با دیگری فرق دارد.
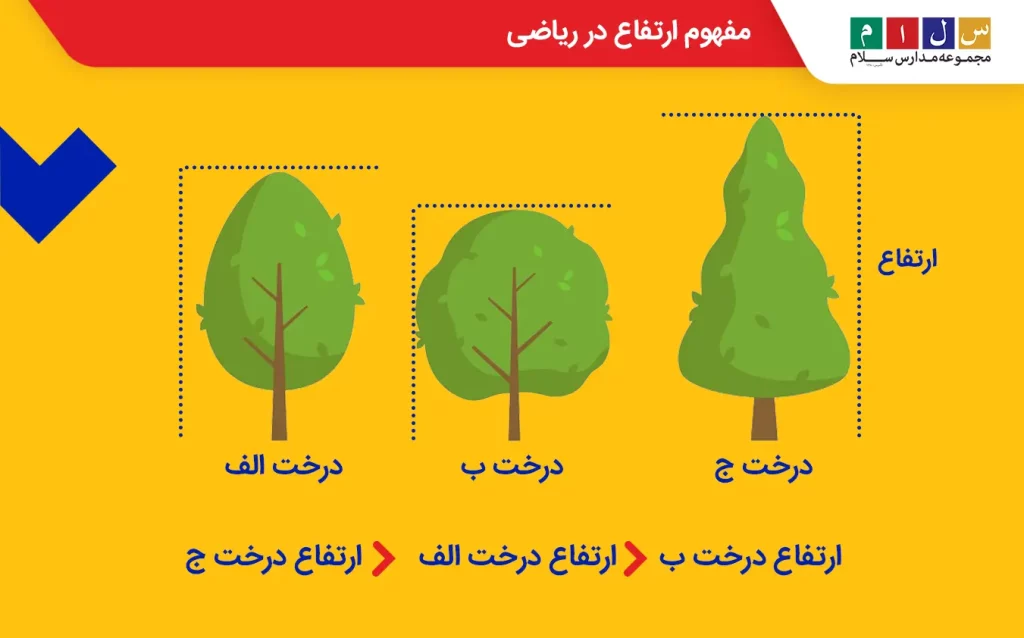
البته گاهی اوقات برای اندازه‌گیری فاصله یک جسم از سطح زمین یا موقعیت یک شئ نسبت به شئ دیگر از اصطلاح ارتفاع بسیار استفاده میشود، مانند سنجش فاصله یک هواپیمای درحال پرواز از سطح زمین. در بخش‌های بعدی شما را با مفهوم ارتفاع در اشکال هندسی آشنا خواهیم کرد.
اولین نفری باشید که از اخبار و اطلاعیه‌های مرتبط با پایه تحصیلیتان باخبر میشود!
ارتفاع در اشکال هندسی دوبعدی
اشکال هندسی دوبعدی به اشکالی گفته میشود که دارای دو بعد طول و عرض هستند، مانند مربع، مستطیل، لوزی، مثلث، متوازی‌الاضلاع، ذوزنقه و غیره. ارتفاع در این اشکال برابر با اندازه پارهخطی است که رأس را به ضلع مقابلش وصل می‌کند و بر آن عمود است. این یعنی اینکه زاویه بین ارتفاع و آن ضلع، قائمه یا ۹۰ درجه است. ارتفاع در اشکال دوبعدی برای محاسبه مساحت بسیار کاربردی است. در ادامه، ارتفاع اشکال هندسی چندضلعی و دوبعدی مختلف را بررسی می‌کنیم.
ارتفاع در مثلث
مثلث یکی از اشکال هندسی دوبعدی است که دارای سه رأس و سه ضلع است. ارتفاع مثلث پارهخطی است که از رأس‌های مثلث رسم شده و بر اضلاع مقابل یا امتداد آن‌ها عمود است. ضلعی را که ارتفاع بر آن عمود است قاعده مثلث می‌نامند. ازآنجا که مثلث سه رأس و سه ضلع دارد، می‌توان نتیجه گرفت که این شکل هندسی دارای سه ارتفاع و سه قاعده است. شکل زیر این موضوع را به‌خوبی نشان می‌دهد.
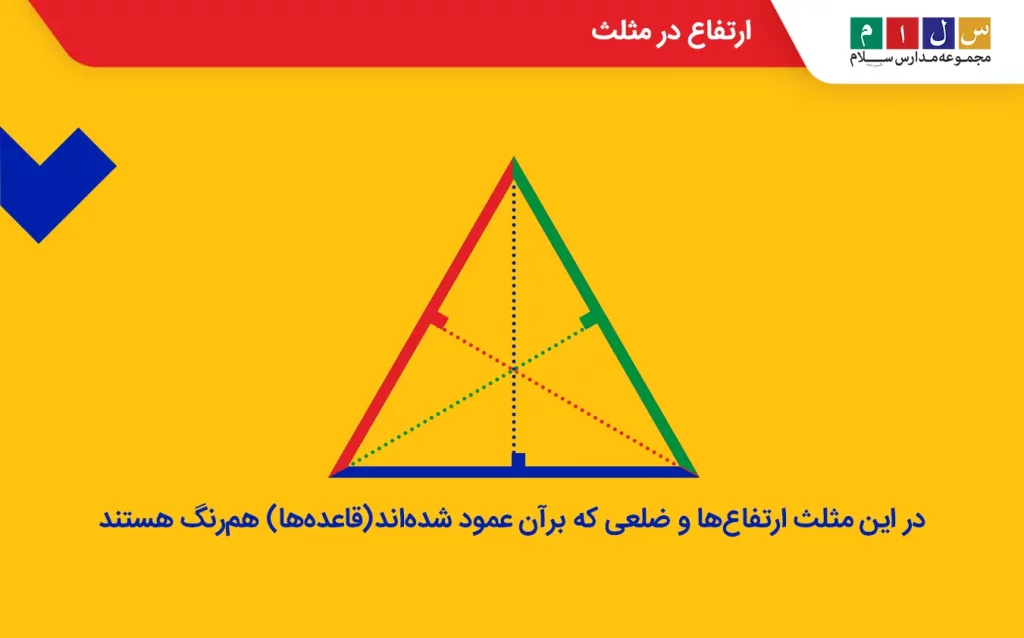
توجه داشته باشید که ارتفاع‌های مثلث مانند شکل بالا همواره داخل مثلث قرار نمی‌گیرند و ممکن است با توجه به زاویه‌های داخلی مثلث، خارج از مثلث رسم شوند. برای بررسی این موضوع، مثلث‌های مختلف را با هم بررسی می‌کنیم.
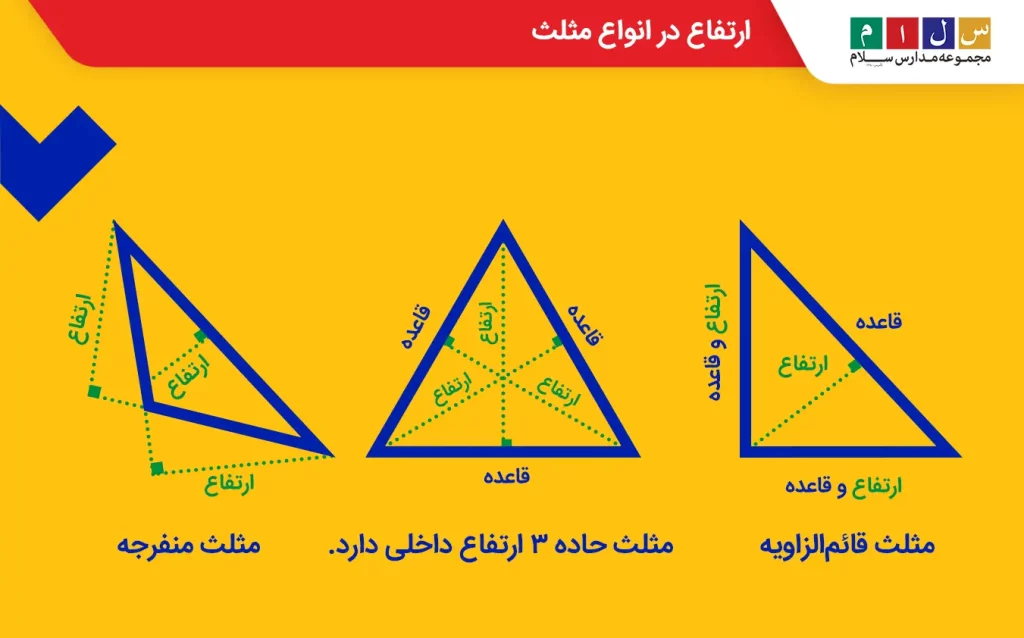
- ارتفاع مثلث حاده: مثلث حاده مثلثی است که اندازه هر یک از زوایای داخلی آن کمتر از ۹۰ درجه است. در این نوع مثلث تمام ارتفاع‌ها داخل مثلث قرار می‌گیرند.
- ارتفاع مثلث منفرجه: مثلث منفرجه به مثلثی گفته میشود که اندازه یکی از زاویه‌های داخلی آن بیشتر از ۹۰ درجه است. در این نوع مثلث‌ها یکی از ارتفاع‌ها درون مثلث و دو تای دیگر در بیرون از مثلث قرار دارند. دو ارتفاع خارجی از رأس‌های زاویه حاده و ارتفاع داخلی از رأس زاویه منفرجه که بیشتر از ۹۰ درجه است رسم میشود.
- ارتفاع مثلث قائم‌الزاویه: مثلث قائم‌الزاویه مثلثی است که یکی از زاویه‌های داخلی آن ۹۰ درجه است و دو ضلع تشکیل‌دهنده آن بر هم عمودند. این دو ضلع چون بر هم عمود هستند، به‌عنوان دو ارتفاع مثلث هم محسوب می‌شوند. ارتفاع سوم این نوع مثلث پارهخطی است که از رأس زاویه قائمه رسم میشود.
ارتفاع در متوازی الاضلاع
متوازی‌الاضلاع یک چهارضلعی است که از چهار رأس تشکیل شده است. در متوازی‌الاضلاع زوایای مقابل با هم برابرند و هر زاویه مکمل زاویه مجاور خود است. ارتفاع در متوازی‌الاضلاع پارهخطی است که یک رأس را به ضلع مقابلش یا امتداد آن وصل می‌کند و بر آن عمود است. درواقع، ارتفاع، فاصله عمودی دو ضلع مقابل و موازی را نشان می‌دهد. ضلعی که ارتفاع بر آن عمود است قاعده متوازی‌الاضلاع نام دارد. در شکل زیر ارتفاع و قاعده متوازی‌الاضلاع را نشان داده‌ایم.
ارتفاع در ذوزنقه
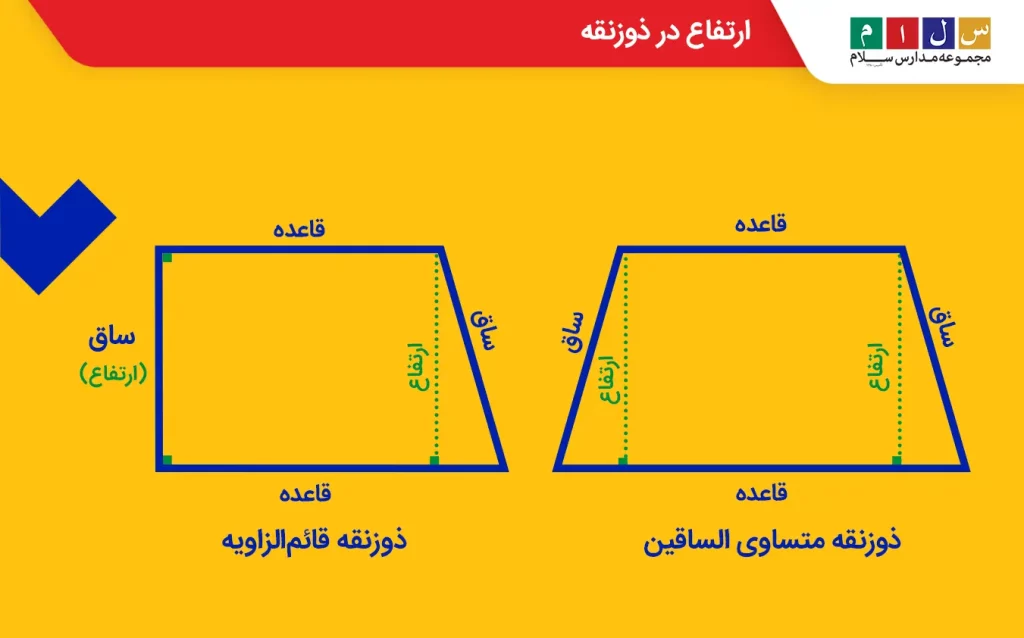
ذوزنقه یکی از اشکال هندسی دوبعدی است که چهار ضلع و چهار رأس دارد. دو تا از ضلع‌های روبه‌روی ذوزنقه با هم موازی و دو تای دیگر آن غیرموازی هستند. دو ضلع غیرموازی را ساق ذوزنقه می‌نامند. ارتفاع در ذوزنقه پارهخطی عمودی است که فاصله بین این دو ضلع موازی و مقابل را نمایش می‌دهد.
اگر یکی از ساق‌های ذوزنقه بر دو ضلع مقابل یعنی قاعده‌ها عمود باشد، ذوزنقه را قائم‌الزاویه می‌نامیم. در این حالت، این ساق عمود، ارتفاع آن نیز خواهد بود.
ارتفاع در اشکال هندسی سه بعدی
تعریف ارتفاع در اشکال سهبعدی متفاوت از اشکال دوبعدی است. اشکالی مانند مکعب، منشور، هرم، مخروط و غیره ازجمله اشکال هندسی سهبعدی هستند که مفهوم ارتفاع در محاسبه حجم آن‌ها مورد استفاده قرار می‌گیرد. در ادامه ارتفاع اشکال هندسی سهبعدی را مورد بررسی قرار می‌دهیم. پیشنهاد می‌کنیم برای آشنایی با کاربرد ارتفاع در محاسبه مساحت و حجم اشکال مختلف، مقاله محیط و مساحت و حجم اشکال هندسی را مطالعه کنید.
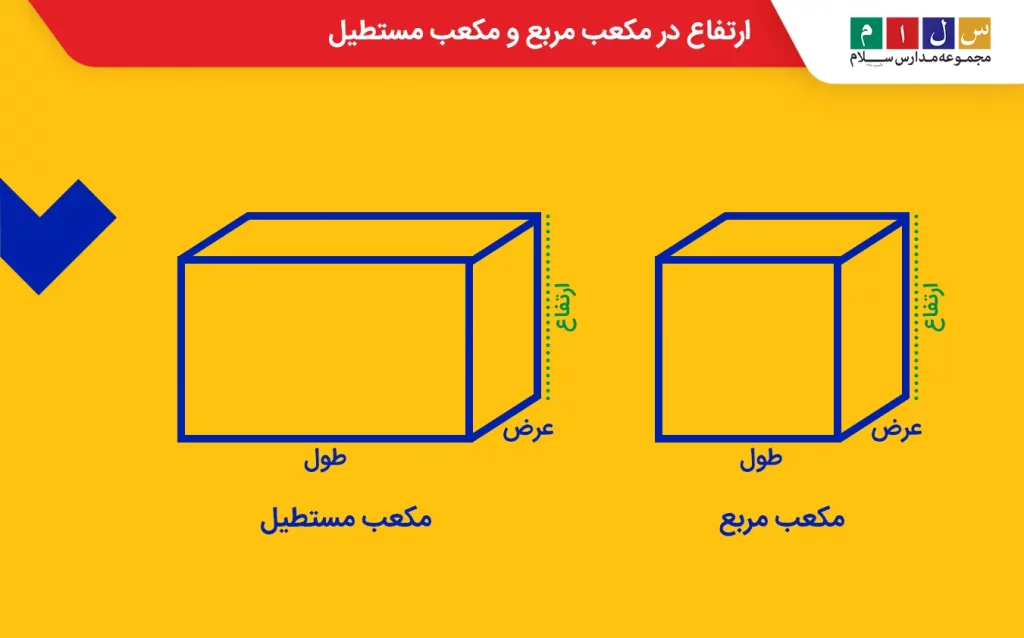
ارتفاع در مکعب مربع و مکعب مستطیل
مکعب مربع و مکعب مستطیل هر دو ازجمله اشکال هندسی سهبعدی هستند که شش وجه دارند. تفاوت این دو شکل در این است که مکعب مربع شش وجه مربعی و مکعب مستطیل شش وجه مستطیلی دارد. ارتفاع در این دو شکل برابر با فاصله عمودی دو وجه موازی است. در مکعب مربع مقدار ارتفاع برابر با اندازه طول و عرض آن است.
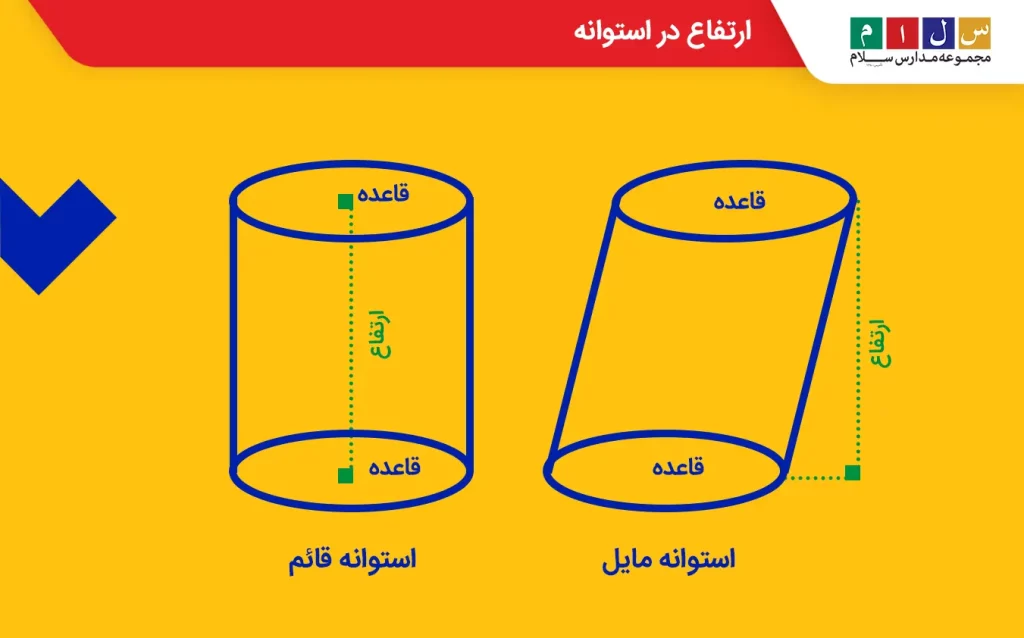
ارتفاع در استوانه
استوانه یک شکل سهبعدی است که از دو وجه مسطح دایره‌ای و یک وجه منحنی‌شکل تشکیل شده است. به فاصله عمودی دو وجه مسطح که قاعده نام دارند، ارتفاع گفته میشود.
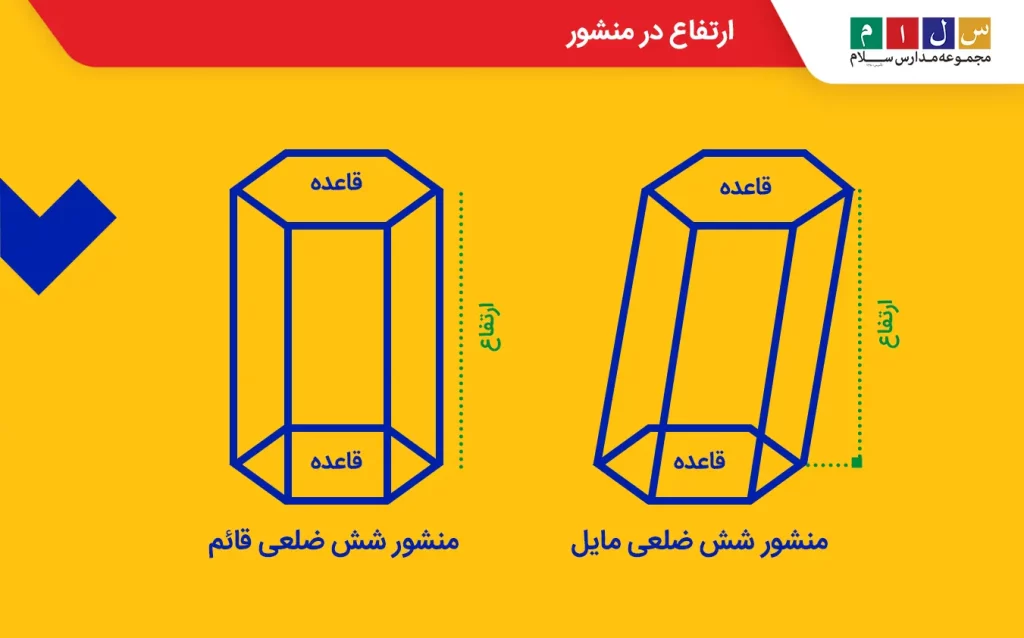
ارتفاع در منشور
منشور یکی از اشکال چندوجهی است که از دو وجه چندضلعی به‌نام قاعده و چند وجه جانبی به‌شکل مربع، مستطیل یا متوازی‌الاضلاع ساخته میشود. ارتفاع در این شکل هندسی برابر با فاصله عمودی بین دو قاعده است.
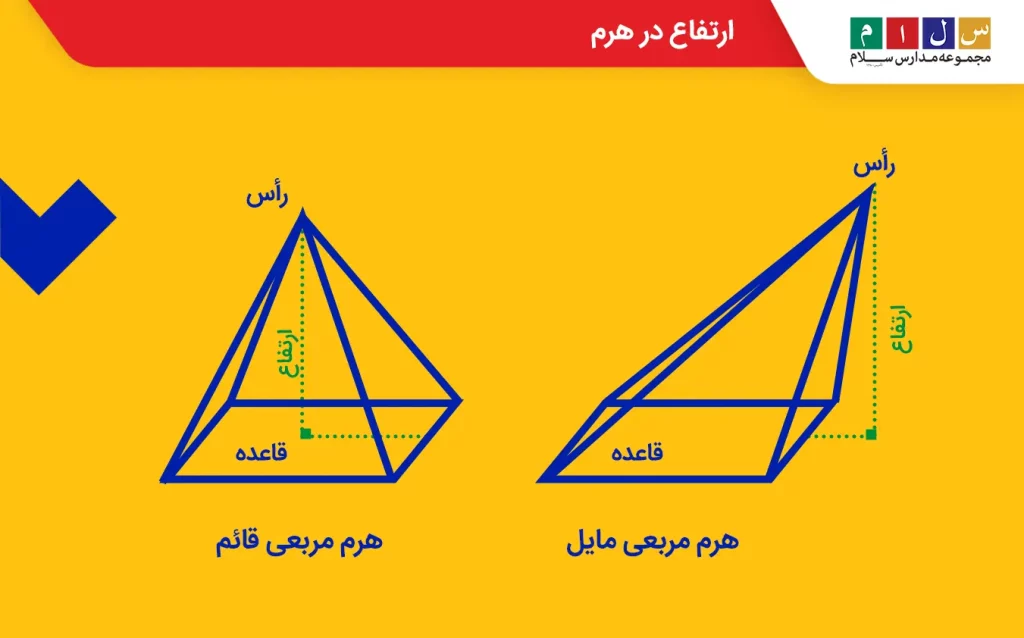
ارتفاع در هرم
هرم یکی دیگر از اشکال چندوجهی است. این شکل هندسی از یک وجه چندضلعی و چند وجه جانبی مثلثی تشکیل شده است. وجه‌های مثلثی در یک نقطه به‌نام رأس به یکدیگر می‌رسند. در هرم‌ها ارتفاع بهصورت پارهخطی تعریف میشود که از رأس هرم عمود بر قاعده رسم میشود.
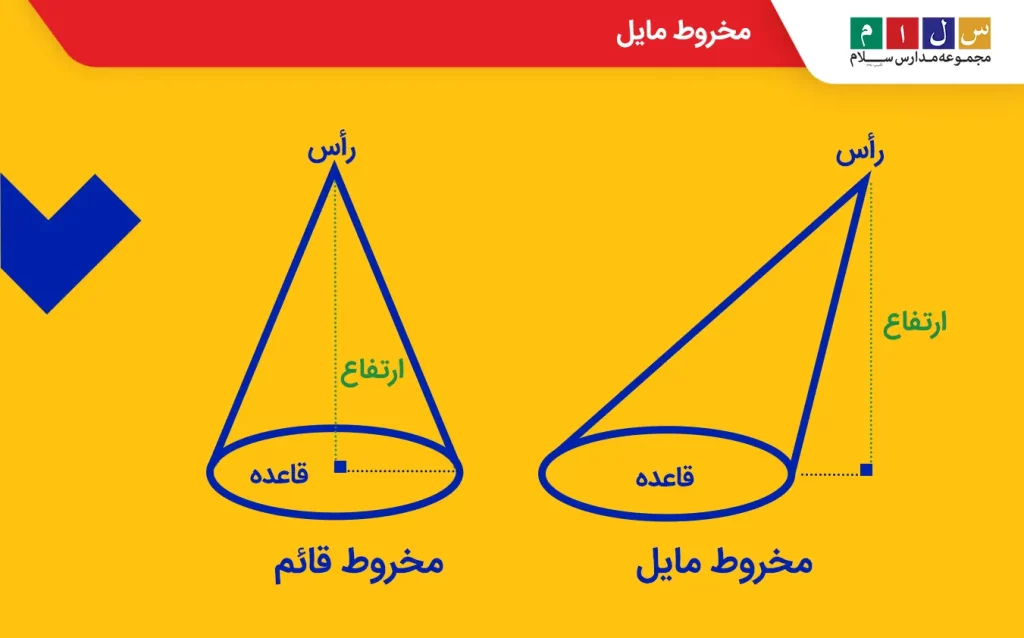
ارتفاع در مخروط
مخروط شکلی سهبعدی شامل یک وجه دایره‌ای به‌نام قاعده، یک وجه منحنی‌شکل و یک رأس است. ارتفاع مخروط پارهخطی است که از رأس رسم شده و بر قاعده که روبه‌روی رأس قرار می‌گیرد عمود است.
سخن پایانی
در این آموزش، درمورد مفهوم ارتفاع در ریاضی صحبت کردیم و گفتیم که ارتفاع برابر با فاصله بین بالاترین و پایینترین نقطه یک شکل است. تعریف این مفهوم هندسی در اشکال هندسی دوبعدی و سهبعدی متفاوت است. در اشکال دوبعدی، ارتفاع به پارهخطی گفته میشود که از یک رأس بر ضلع مقابل یا امتداد آن عمود میشود، اما در اشکال سهبعدی بسته به شکل موردنظر، تعریف ارتفاع می‌تواند متفاوت باشد.
سؤالات متداول
- ارتفاع چیست؟
ارتفاع در ریاضیات، به فاصله بالاترین نقطه و پایینترین نقطه یک جسم یا شکل گفته میشود. - ارتفاع در اشکال هندسی دوبعدی چگونه است؟
ارتفاع در اشکال دوبعدی پارهخطی است که از یک رأس رسم شده و بر ضلع مقابل یا امتداد آن ضلع عمود است. - ارتفاع در اشکال هندسی سهبعدی چیست؟
در اشکال سهبعدی، ارتفاع برابر با فاصله عمودی بین دو وجه مقابل و موازی یا دو قاعده است. همچنین، در اشکالی مانند هرم و مخروط که یک رأس در بالای قاعده دارند، ارتفاع بهصورت پارهخطی است که از رأس رسم شده و بر قاعده عمود است.
