تعریف بیضی به زبان ساده + ویژگی ها و فرمول ها

احتمالاً در کتاب‌‌ها و مجلات علمی خوانده‌‌اید که سیاره‌‌ها در مسیری بیضی‌‌شکل به دور خورشید می‌‌چرخند و مدار گردش ماه به دور زمین نیز به‌‌شکل یک بیضی است. علاوه‌‌بر این‌‌ها نمونه‌‌های دیگری هم در زندگی روزمره ما به چشم می‌‌خورند که شکل ظاهری آن‌‌ها به‌‌صورت یک دایره کشیده یا همان بیضی دیده می‌‌شود، ازجمله تخم‌‌مرغ، راکت بدمیمنتون، مسیر دویدن در یک استادیوم ورزشی و غیره. در این مقاله قصد داریم ضمن آشنا کردن شما با شکل بیضی، اصطلاحات مهم، ویژگی‌‌ها و فرمول‌‌های مختلف این شکل هندسی را توضیح دهیم.

بیضی چیست؟

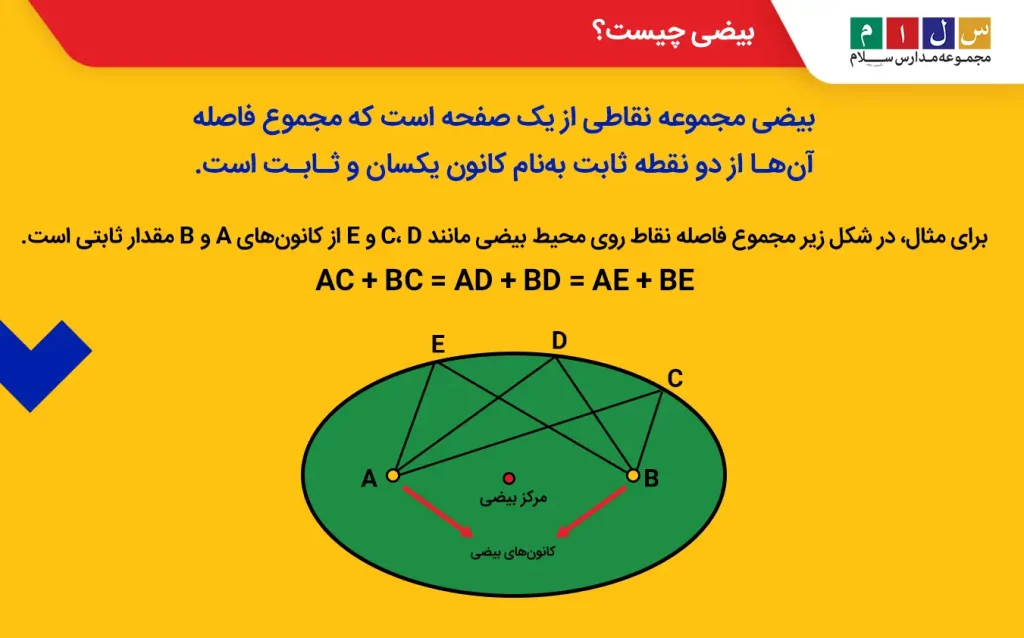
بیضی مجموعه نقاطی از یک صفحه است که مجموع فاصله آن‌‌ها از دو نقطه ثابت به‌‌نام کانون یکسان و ثابت است. بیضی مانند دایره‌‌ای به نظر می‌‌رسد که از دو طرف کشیده شده است. بنابراین، تفاوت بیضی و دایره را می‌‌توان در جمله زیر خلاصه کرد:

دایره نوعی بیضی است که دو کانون آن در یک نقطه یعنی مرکز دایره قرار دارند. درحالی‌‌که در یک بیضی کانون‌‌ها در دو طرف مرکز آن واقع شده‌‌اند و فاصله آن‌‌ها از مرکز بیضی با هم برابر است.

ویژگی های بیضی

بیضی به‌‌دلیل شکل خاصی که دارد دارای ویژگی‌‌هایی است که آشنایی با آن‌‌ها در محاسبات مربوط به این شکل هندسی حائز اهمیت است. این ویژگی‌‌ها را در ادامه بیان می‌‌کنیم:

• یک بیضی ۲ کانون دارد که حاصل‌‌جمع فاصله هر نقطه روی محیط بیضی از آن‌‌ها مقدار یکسان و ثابتی است.
• مرکز بیضی دقیقاً بین دو کانون و در راستای آن‌‌ها قرار دارد.
• بیضی ۴ رأس دارد. محل برخورد قطرهای بزرگ و کوچک بیضی با محیط آن را رأس بیضی می‌‌گویند.
• محور اصلی یا بزرگ بیضی که قطر بزرگ نیز نام دارد، طولانی‌‌ترین قطر بیضی است که از کانون‌‌ها و مرکز آن عبور می‌‌کند. نصف محور اصلی را نیم‌‌محور بزرگ یا شعاع بزرگ بیضی می‌‌نامند.
• محور فرعی یا کوچک بیضی که به آن قطر کوچک نیز می‌‌گویند، کوتاه‌‌ترین قطر بیضی است که بر محور اصلی عمود است و از مرکز بیضی نیز عبور می‌‌کند. نصف محور فرعی، نیم‌‌محور کوچک یا شعاع کوچک بیضی نامیده می‌‌شود. 
• بیضی بی‌‌نهایت قطر دارد اما در محاسبات مربوط به آن تنها دو قطر کوچک و بزرگ مورد استفاده قرار می‌‌گیرد.
• قطر بزرگ و کوچک بیضی خط تقارن آن نیز هستند.
• بیضی دارای تقارن مرکزی است و مرکز تقارن آن در مرکز یا به‌‌عبارتی، محل برخورد قطرهای بزرگ و کوچک قرار دارد.

رسم بیضی

بیضی را می‌‌توان به‌‌راحتی رسم کرد. ابزارهای موردنیاز برای رسم بیضی عبارت‌‌اند از:

• دو عدد پونز
• یک تکه نخ یا کاموا
• مداد یا خودکار
• کاغذ

ابتدا مانند شکل زیر پونزها را در یک فاصله دلخواه از هم روی کاغذ قرار دهید. سپس، دو سر یک تکه نخ یا کاموا را به هم گره زده و به‌‌صورت یک حلقه درآورید. مطابق شکل، حلقه نخ را دور پونزها قرار داده و با کمک یک مداد نخ را تا جایی بکشید که به‌‌صورت یک مثلث درآید. در آخر، با حفظ کشیدگی نخ مداد را روی کاغذ جابه‌‌جا کنید تا کل منحنی بیضی کشیده شود.

خروج از مرکز بیضی

خروج از مرکز معیاری است که نشان می‌‌دهد بک بیضی چقدر کشیدگی دارد. هرچه خروج از مرکز به صفر نزدیک باشد، شکل بیضی به دایره نزدیک‌‌تر است اما هرچه به یک نزدیک باشد، بیضی کشیدگی بیشتری خواهد داشت. خروج از مرکز با نماد e نشان داده می‌‌شود و مقدار آن از رابطه زیر به‌‌دست می‌‌آید:

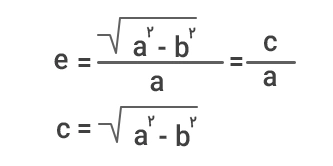
• a: شعاع بزرگ بیضی
• b: شعاع کوچک بیضی
• c: نصف فاصله دو کانون بیضی
• e: خروج از مرکز بیضی

معادله بیضی

اگر محور اصلی (بزرگ) یک بیضی افقی باشد آن را بیضی افقی می‌‌نامیم. معادله این نوع بیضی به‌‌صورت زیر است:

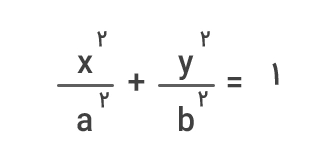
• a: طول نیم‌‌محور (شعاع) بزرگ بیضی
• b: طول نیم‌‌محور (شعاع) کوچک بیضی

اگر بیضی عمودی باشد یعنی محور اصلی (بزرگ) آن عمودی باشد، معادله بیضی به‌‌صورت زیر خواهد بود:

در این معادله نیز a نیم‌‌محور بزرگ و b نیم‌‌محور کوچک بیضی است.

محیط بیضی

محیط یک بیضی برابر است با اندازه طول منحنی آن. همان‌‌طور که در مقاله محیط بیضی نیز اشاره کردیم، برای محیط بیضی فرمول واحد و دقیقی وجود ندارد و می‌‌توان از فرمول‌‌های متعددی برای محاسبه مقدار آن استفاده کرد. یکی از فرمول‌‌های رایج و شناخته‌‌شده‌‌ای که مقدار تقریبی محیط بیضی را به ما می‌‌دهد، فرمول زیر است:

در این فرمول a نیم‌‌محور بزرگ و b نیم‌‌محور کوچک بیضی است. 

مساحت بیضی

به اندازه سطح داخلی یک بیضی، مساحت بیضی می‌‌گویند. اگر نیم‌‌محور بزرگ بیضی را با a و نیم‌‌محور کوچک آن را با b نشان دهیم، مساحت بیضی را می‌‌توان از فرمول زیر محاسبه کرد:

A=πab

درصورتی‌‌که a و b مساوی باشند، فرمول مساحت بیضی تبدیل به فرمول مساحت دایره خواهد شد.

مثال هایی از شکل بیضی

مثال ۱: معادله یک بیضی به‌‌صورت زیر است. اندازه محورهای بزرگ و کوچک و خروج از مرکز این بیضی را تعیین کنید.

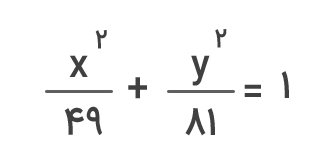
جواب: با توجه به شکل معادله بیضی می‌‌توان معادله داده‌‌شده را به‌‌شکل زیر نوشت:

این معادله نشان می‌‌دهد که طول نیم‌‌محور بزرگ بیضی برابر با ۹ و طول نیم‌‌محور کوچک آن مساوی با ۷ است. بنابراین، اندازه محورهای بزرگ و کوچک این بیضی به‌‌صورت زیر خواهد بود:

۹ × ۲= ۱۸
۷× ۲ = ۱۴

اکنون می‌‌توانیم با کمک نیم‌‌محور بزرگ و کوچک، خروج از مرکز بیضی را محاسبه کنیم. داریم:

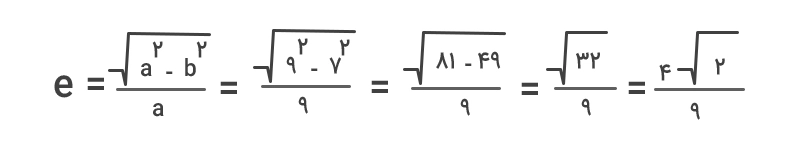
مثال ۲: مختصات رأس‌‌های یک بیضی افقی به‌‌صورت ۰, ۶، ۰,- ۶، ۱۰, ۰ و -۱۰,۰ است، معادله این بیضی را بنویسید.

جواب: با توجه به اطلاعات داده‌‌شده، طول نیم‌‌محور بزرگ و کوچک بیضی برابر است با

a=۱۰
b=۶

درنتیجه معادله بیضی به‌‌صورت زیر خواهد بود:

مثال ۳: محورهای بزرگ و کوچک یک بیضی به‌‌ترتیب برابر با ۵ و ۳ سانتی‌‌متر است. مساحت این بیضی را بیابید.

جواب: برای تعیین مساحت بیضی ابتدا باید اندازه شعاع یا نیم‌‌محورهای آن را به‌‌دست آوریم، سپس مقدار مساحت را محاسبه کنیم. بنابراین، خواهیم داشت:  

a = ۵ ÷ ۲=۲/۵ cm
b = ۳÷ ۲ =۱/۵ cm
A = π a b = ۳/۱۴ × ۲/۵ ×۱/۵ = ۱۱/۷۷۵ cm۲

سخن پایانی

در این مطلب به معرفی یکی دیگر از اشکال هندسی به‌‌نام بیضی پرداختیم و ویژگی‌‌های هندسی آن را بیان کردیم. بیضی مانند دایره‌‌ای است که از دو طرف کشیده شده است و به همین دلیل، قطرها و درنتیجه شعاع‌‌های متفاوتی دارد. دو قطر اصلی بیضی که محور بزرگ و محور کوچک نام دارند و در فرمول‌‌های بیضی بسیار مورد استفاده قرار می‌‌گیرند، در مرکز این شکل هندسی یکدیگر را قطع کرده و بر هم عمودند. در این مقاله علاوه‌‌بر معرفی خواص بیضی، درمورد معادله و فرمول‌‌های آن نیز صحبت کرده و برای درک بهتر چند مثال حل کردیم. امیدواریم این آموزش برایتان مفید بوده باشد.

سؤالات متداول

1. بیضی چیست؟
   طبق تعریف بیضی در هندسه، بیضی به مجموعه نقاطی از یک صفحه گفته می‌‌شود که حاصل‌‌جمع فاصله آن‌‌ها از دو نقطه ثابت به‌‌نام کانون مساوی با مقدار ثابتی است.
2. آیا بیضی مرکز تقارن دارد؟
   بله. مرکز تقارن بیضی در مرکز آن قرار دارد.
3. بیضی چند خط تقارن دارد؟
   بیضی تنها ۲ خط تقارن دارد.
4. فرمول محیط بیضی چیست؟
   فرمول‌‌های مختلفی برای محاسبه محیط بیضی وجود دارد که در مقاله محیط بیضی به آن‌‌ها اشاره کردیم.
5. فرمول مساحت بیضی چیست؟
   مساحت بیضی از حاصل‌‌ضرب عدد پی در شعاع‌‌های کوچک و بزرگ آن به‌‌دست می‌‌آید.