کسر چیست ؟ | معرفی انواع کسر و عملیات ریاضی در آن ها

زمانی که یک کیک یا یک پیتزا را به قسمت‌های مساوی تقسیم می‌کنیم، هر قسمت از آن‌ها بخشی از کل کیک یا پیتزا را نشان می‌دهند. کسرها نیز به‌عنوان یک مفهوم ریاضی تعریفی مشابه همین مثال دارند. درحقیقت یک کسر نشان‌دهنده بخشی از یک کل است. برای اینکه با مفهوم کسر در ریاضی بیشتر آشنا شوید و بدانید کسر چیست با ادامه این آموزش همراه باشید.

کسر چیست؟

کسرها مقادیری هستند که بخش‌هایی از یک کل یا مجموعه را نمایش می‌دهند. برای همین یک کسر از دو قسمت صورت و مخرج تشکیل شده است. صورت نشان‌دهنده بخش‌های موردنظر از یک کل است و مخرج نیز نمایانگر تعداد کل بخش‌ها است.

به‌عنوان مثال، یک کیک را در نظر بگیرید که به ۸ قسمت مساوی تقسیم شده است. یک تکه از آن را برمی‌داریم و در یک بشقاب قرار می‌دهیم. تکه کیکی که برداشته شده است معادل ۱ قسمت از ۸ قسمت است. بنابراین می‌گوییم (یک‌هشتم) کیک در بشقاب قرار دارد. ۱ صورت کسر و ۸ مخرج آن است. در نمایش کسرها مقدار صورت و مخرج را با یک خط افقی از هم جدا می‌کنیم.

نمایش کسرها روی محور اعداد

فرض کنید می‌خواهیم کسر را روی محور اعداد نشان دهیم. مقدار صورت این کسر از مخرج آن کوچک‌تر است. این یعنی اینکه مقدار کسر از ۱ کمتر خواهد بود. بنابراین، برای نشان دادن آن روی محور کافی‌ست مانند شکل زیر ۰ و ۱ را روی محور مشخص کرده و فاصله بین آن‌ها را به ۸ قسمت مساوی تقسیم کنیم. 

حالا از صفر شروع کرده و از ۸ قسمت مساوی تنها به‌اندازه ۱ قسمت جلو می‌رویم و آن را علامت‌گذاری می‌کنیم. مکان علامت‌گذاری‌شده کسر را نشان می‌دهد. اگر به‌جای این کسر بخواهیم کسر را نشان دهیم باید به‌اندازه ۲ قسمت کوچک بشماریم. به‌همین ترتیب برای سایر کسرها با توجه به مقدار صورت آن‌ها همین کار را انجام می‌دهیم.

همان‌طور که در تصویر زیر هم می‌بینید کسر روی ۱ منطبق شده است، به این معنی که مقدار این کسر برابر با ۱ است. به‌طور کلی، اگر صورت و مخرج یک کسر برابر باشند، مقدار آن کسر مساوی با ۱ خواهد بود.

انواع کسرها

کسرها براساس مقدار صورت و مخرج به انواع مختلفی دسته‌بندی می‌شوند. در جدول زیر، انواع رایج کسرها را با مثال معرفی کرده‌ایم. 

انواع کسرها	تعریف	مثال
کسر کوچک‌تر از واحد	کسری که مقدار صورت از مخرج آن کوچک‌تر است.
کسر بزرگ‌تر از واحد	کسری که مقدار صورت از مخرجش بزرگ‌تر است.
عدد مخلوط	کسری که شامل یک عدد کامل و یک کسر کوچک‌تر از واحد است.
کسرهای با مخرج مساوی	کسرهایی که مقدار مخرج آن‌ها یکسان است.
کسرهای با مخرج نامساوی	کسرهایی که مقدار مخرج آن‌ها متفاوت است.
کسرهای مساوی	کسرهایی که پس از ساده‌سازی مقدار یکسانی دارند.

تبدیل کسر به اعشار و درصد

منظور از تبدیل کسر به عدد اعشاری، نوشتن عدد اعشاری معادل کسر است. برای مثال، اگر بخواهیم کسر(سه‌چهارم) را به‌صورت عدد اعشاری بنویسیم، کافی‌ست صورت یعنی ۳ را بر مخرج یعنی ۴ تقسیم کنیم. خواهیم داشت:

البته برای تبدیل یک کسر به عدد اعشاری روش دیگری غیر از تقسیم کردن نیز وجود دارد. اگر می‌خواهید با این روش آشنا شوید می‌توانید به مقاله تبدیل کسر به اعشار مراجعه کنید. در آنجا به‌طور کامل دراین‌باره صحبت کرده‌ایم.

فرض کنید می‌خواهیم همین کسر را به‌صورت درصد نمایش دهیم. برای این کار فقط کافی‌ست کسر را در ۱۰۰ ضرب کنیم. خواهیم داشت:

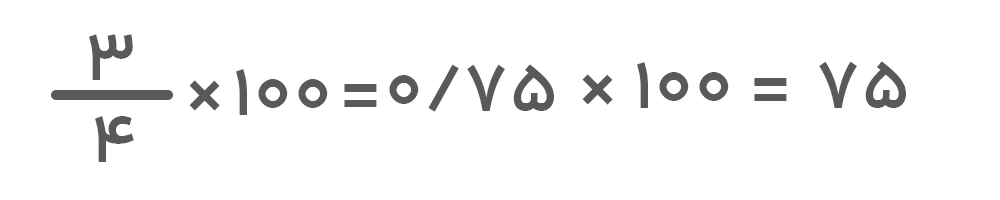
بنابراین، می‌توانیم کسر را به‌صورت %۷۵ نیز نشان دهیم.

تبدیل کسر به عدد مخلوط و بالعکس

کسرهایی که مقدار صورت آن‌ها از مخرج بزرگ‌تر است یا به‌عبارتی کسرهای بزرگ‌تر از واحد را می‌توان به‌صورت عدد مخلوط نوشت. درواقع، اعداد مخلوط درک چنین کسرهایی را برایمان راحت‌تر می‌کنند. برای مثال، درک کسری مانندنسبت به کسر راحت‌تر است چون صورت آن از مخرجش کوچک‌تر است. اما اگر کسر دوم را که یک کسر بزرگ‌تر از واحد است به عدد مخلوط تبدیل کنیم، درک آن آسان‌تر خواهد بود.

روش‌های گوناگونی برای نمایش کسر به‌صورت عدد مخلوط وجود دارد که در مقاله تبدیل کسر به عدد مخلوط به‌طور مفصل آن‌ها را توضیح داده‌ایم. در اینجا ما تنها به روش گسترده‌نویسی که روش راحت‌تری است بسنده می‌کنیم و با مثالی که در ادامه حل خواهیم کرد آن را آموزش می‌دهیم. 

مثال: کسر  را به‌صورت عدد مخلوط بنویسید.

ابتدا صورت کسر را به اعداد مساوی با مخرج تجزیه می‌کنیم. برای این کار باید بررسی کنیم که چند ۵ در عدد ۱۳ وجود دارد. شکل گسترده صورت کسر به‌صورت زیر خواهد بود:

$$\frac{۱۳}{۵}=\frac{۵+۵+۳}{۵}=\frac{۵}{۵}+\frac{۵}{۵}+\frac{۳}{۵}=۱+۱+\frac{۳}{۵}=۲+\frac{۳}{۵}=۲\frac{۳}{۵}$$

تا اینجا با روش تبدیل کسرها به عدد مخلوط آشنا شدیم. حال این سؤال پیش می‌آید که اگر بخواهیم عدد مخلوط را به کسر تبدیل کنیم باید چه روشی را به‌کار ببریم؟ با یک مثال این حالت را هم بررسی می‌کنیم.

مثال: عدد مخلوط را به کسر تبدیل کنید.

برای تبدیل این عدد به کسر، باید عدد کامل یعنی 4 را در مخرج کسر یعنی 8 ضرب کرده و حاصل آن را با مقدار صورت (۵) جمع کنیم. در آخر مقدار به‌دست‌آمده را در صورت قرار می‌دهیم و مخرج را هم بدون تغییر دادن مقدار آن می‌نویسیم.

$$۴\frac{۵}{۸}=\frac{۴\times <!--\; \times \; -->۸+۵}{۸}=\frac{۳۲+۵}{۸}=\frac{۳۷}{۸}$$

ساده کردن کسرها

منظور از ساده کردن کسرها نوشتن آن‌ها به ساده‌ترین شکل ممکن است طوری که صورت و مخرج آن‌ها نسبت به هم اول باشند یا به‌عبارتی عامل مشترکی غیر از ۱ نداشته باشند. ازجمله روش‌های رایج برای ساده‌سازی کسرها استفاده از ب م م یا بزرگ‌ترین مقسوم‌علیه مشترک صورت و مخرج است. به مثال زیر توجه کنید:

می‌خواهیم کسررا ساده کنیم. نخستین گام برای ساده‌سازی این کسر این است که ب م م ۴۲ و ۵۶ را تعیین کنیم. با توجه به روش‌هایی که برای تعیین ب م م دو عدد وجود دارد، می‌دانیم که بزرگ‌ترین مقسوم‌علیه مشترک ۴۲ و ۵۶ مساوی با ۱۴ است. بنابراین، کافی‌ست صورت و مخرج را بر ۱۴ تقسیم کنیم تا شکل ساده کسر به‌دست آید.

$$\frac{۴۲÷<!--\; ÷\; -->۱۴}{۵۶÷<!--\; ÷\; -->۱۴}=\frac{۳}{۴}$$

همان‌طور که می‌بینید صورت و مخرج کسر به‌دست‌آمده نسبت به هم اول هستند و بیشتر از این نمی‌توان کسر داده‌شده را ساده کرد.

توجه داشته باشید که ساده‌سازی این کسر را می‌توان با کمک عامل‌های مشترک دیگری مانند ۷ و ۲ هم انجام داد اما در این صورت مراحل ساده‌سازی طولانی‌تر می‌شود. محاسبات زیر این موضوع را به‌خوبی نشان می‌دهد.

$$\frac{۴۲÷<!--\; ÷\; -->۷}{۵۶÷<!--\; ÷\; -->۷}=\frac{۶÷<!--\; ÷\; -->۲}{۸÷<!--\; ÷\; -->۲}=\frac{۳}{۴}$$

تساوی کسرها

مفهوم تساوی کسرها به این اشاره دارد که دو یا چند کسر مقدار یا نسبت برابری را نشان می‌دهند. چنین کسرهایی اگرچه صورت و مخرج متفاوتی درمقایسه با یکدیگر دارند، اما اگر ساده شوند یک مقدار را نشان می‌دهند. برای مثال، دو کسر دو کسر مساوی هستند زیرا اگر  را به روشی که در بخش قبل گفتیم ساده کنیم، مقدار آن دقیقاً برابر با خواهد بود.

$$\frac{۱۸}{۲۴}=\frac{۱۸÷<!--\; ÷\; -->۶}{۱۴÷<!--\; ÷\; -->۶}=\frac{۳}{۴}$$

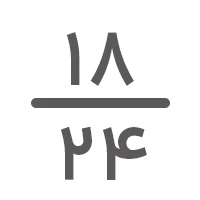
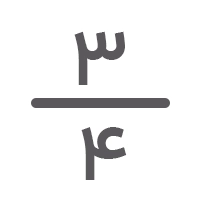
اگر یک کسر داشته باشیم و بخواهیم کسرهای مساوی با آن را به‌دست آوریم، کافی‌ست صورت و مخرج را در یک عدد ضرب یا بر یک عدد تقسیم کنیم. به‌عنوان مثال، کسرهای مساوی با را می‌توان به‌صورت زیر تعیین کرد:

$$\frac{۴}{۱۲}=\frac{۴÷<!--\; ÷\; -->۲}{۱۲÷<!--\; ÷\; -->۲}=\frac{۴÷<!--\; ÷\; -->۴}{۱۲÷<!--\; ÷\; -->۴}$$ $$\frac{۴}{۱۲}=\frac{۲}{۶}=\frac{۱}{۳}$$

با عمل ضرب هم می‌توانیم کسرهای مساوی را به‌دست آوریم:

$$\frac{۴}{۱۲}=\frac{۴\times <!--\; \times \; -->۲}{۱۲\times <!--\; \times \; -->۲}=\frac{۴\times <!--\; \times \; -->۳}{۱۲\times <!--\; \times \; -->۳}$$ $$\frac{۴}{۱۲}=\frac{۸}{۲۴}=\frac{۱۲}{۳۶}$$

مقایسه ی کسرها

برای مقایسه مقدار یک کسر نسبت به کسر دیگر یا به‌عبارتی تعیین کسر بزرگ‌تر یا کوچک‌تر قبل از هر چیز باید به مقدار مخرج کسرها توجه کنیم. چند حالت خواهیم داشت:

• اگر مخرج‌ها مساوی باشند، صورت‌ها را بررسی می‌کنیم. در این حالت، کسری بزرگ‌تر خواهد بود که مقدار صورت آن بزرگ‌تر است .
• اگر مخرج‌ها نامساوی ولی صورت‌ها مساوی باشند، کسری بزرگ‌تر خواهد بود که مقدار مخرج آن کوچک‌تر است..

• اگر هم مخرج‌ها و هم صورت‌ها نامساوی باشند، با کمک روش‌های مقایسه ی کسرها مانند روش طرفین وسطین کسر بزرگ‌تر را تعیین می‌کنیم.

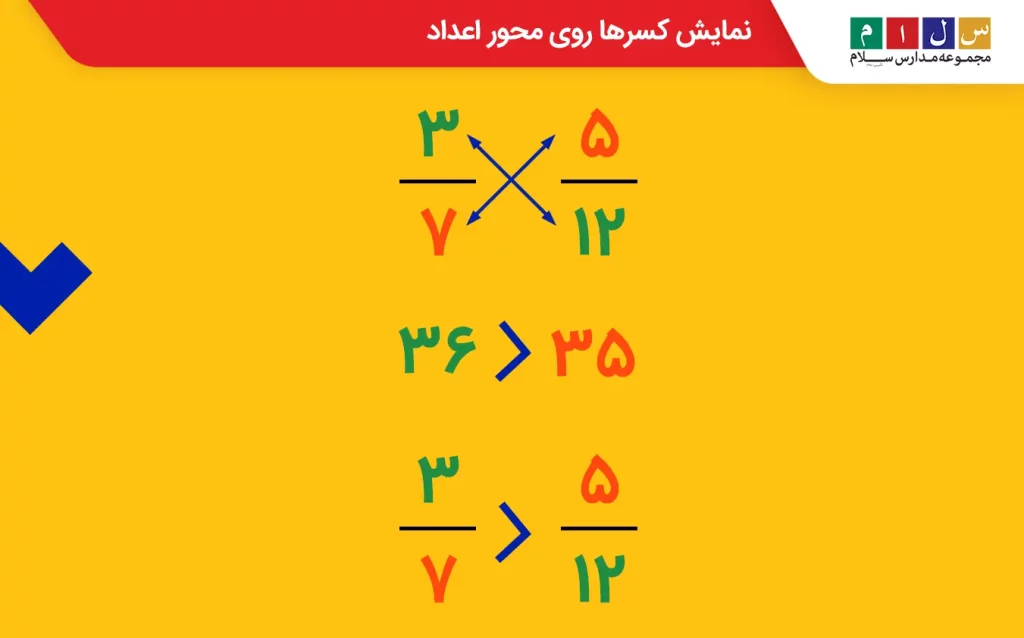
مثال: کسر را مقایسه کنید.

با توجه به اینکه صورت و مخرج هر دو کسر مقادیر متفاوتی دارند، با کمک ضرب متقاطع یا همان طرفین وسطین کسر بزرگ‌تر و کوچک‌تر را مشخص می‌کنیم.

در این روش، صورت کسر اول را در مخرج کسر دوم ضرب کرده و حاصل آن را زیر کسر اول می‌نویسیم. سپس، صورت کسر دوم را در مخرج کسر اول ضرب کرده و مقدار آن را زیر کسر دوم یادداشت می‌کنیم. حاصل‌ضرب هر کدام بزرگ‌تر بود، کسر موردنظر در بالای آن هم بزرگ‌تر است.

جمع و تفریق کسرها

عمل جمع و عمل تفریق در کسرها مشابه هم است. ازاین‌رو، تمام قوانینی که برای جمع کسرها به‌کار می‌بریم در تفریق کسرها نیز صدق می‌کند. 

• اگر مخرج کسرها یکسان باشد، مخرج را ثابت نگه می‌داریم و صورت‌ها را با توجه به اینکه بین آن‌ها علامت جمع یا تفریق است، با هم جمع یا از هم کم می‌کنیم.

$$\frac{۴}{۱۱}+\frac{۵}{۱۱}=\frac{۹}{۱۱}$$ $$\frac{۷}{۱۰}-<!--\; -\; -->\frac{۵}{۱۱}=\frac{۲}{۱۰}$$

اگر مخرج کسرها متفاوت باشد، با کمک ک م م یا کوچک‌ترین مضرب مشترک، مخرج مشترک می‌گیریم و سپس عمل جمع و تفریق کسرها را انجام می‌دهیم. در ادامه با یک مثال روش انجام آن را توضیح خواهیم داد.

مثال: حاصل‌جمع کسرهای را به‌دست آورید.

ابتدا ک م م مخرج‌ها را تعیین می‌کنیم. ک م م ۱۲ و ۱۸ مساوی با ۳۶ است. پس باید کاری کنیم که مخرج‌ها برابر با ۳۶ شوند. دقت داشته باشید که هر عددی را در مخرج ضرب می‌کنیم باید در صورت هم ضرب شود.

$$\frac{۷}{۱۲}+\frac{۵}{۱۸}=\frac{۲}{۱۰}=\frac{۷\times <!--\; \times \; -->۳}{۱۲\times <!--\; \times \; -->۳}+\frac{۵\times <!--\; \times \; -->۲}{۱۸\times <!--\; \times \; -->۲}=\frac{۲۱}{۳۶}+\frac{۱۰}{۳۶}=\frac{۳۱}{۳۶}$$

ضرب و تقسیم کسرها

انجام ضرب و تقسیم کسرها نیازمند یک‌سری قواعد است که در ادامه آن‌ها را بیان خواهیم کرد.

ضرب کسرها

برای ضرب کسر ها، کافی‌ست صورت‌ها و مخرج‌ها را جداگانه در هم ضرب کنیم. مثلاً برای محاسبه حاصل‌ضرب به‌صورت زیر عمل می‌کنیم:

$$\frac{۲}{۱۵}\times <!--\; \times \; -->\frac{۷}{۳}=\frac{۲\times <!--\; \times \; -->۷}{۱۵\times <!--\; \times \; -->۳}=\frac{۱۴}{۴۵}$$

تقسیم کسرها

برای تقسیم کسر ها، باید مراحل زیر را انجام دهیم:

• کسر اول را ثابت نگه داشته و تغییر نمی‌دهیم.
• علامت تقسیم (÷) را به علامت ضرب (×) تبدیل می‌کنیم.
• سپس کسر دوم را وارونه کرده و جای صورت و مخرج آن را عوض می‌کنیم.

مثال: حاصل تقسیم را تعیین کنید.

$$\frac{۳}{۷}÷<!--\; ÷\; -->\frac{۵}{۱۱}=\frac{۳}{۷}\times <!--\; \times \; -->\frac{۱۱}{۵}=\frac{۳\times <!--\; \times \; -->۱۱}{۷\times <!--\; \times \; -->۵}=\frac{۳۳}{۳۵}$$

سخن پایانی

در این مقاله به تعریف کسر پرداختیم و توضیح دادیم که کسر چیست و چه انواعی دارد. همچنین گفتیم که کسرها نمایانگر بخشی از یک کل هستند و از دو بخش صورت و مخرج تشکیل شده‌اند. به همین خاطر، عملیات ریاضی در آن‌ها تابع قوانین خاصی است. 

با توجه به اینکه در زندگی روزمره از کسرها بسیار استفاده می‌شود، می‌توانید حین تقسیم خوراکی‌ها، خواندن ساعت و کارهایی از این قبیل مفهوم کسر و عملیات ریاضی آن‌ها را مرور کنید. این کار به تثبیت یادگیری شما کمک خواهد کرد.