فهرست مطالب
Toggleاغلب کسرهایی که مقدار صورت و مخرج آنها بزرگ است، محاسبات ریاضی را برایمان دشوارتر میکنند. در چنین مواقعی، بهترین راهکار ساده کردن این کسرها است. منظور از ساده کردن کسر، نوشتن یک کسر به سادهترین شکل ممکن است؛ بهگونهای که صورت و مخرج آن عامل مشترکی غیر از یک نداشته باشند.
در این مقاله، روشهای رایج برای ساده کردن کسرها را به شما خواهیم آموخت.
ساده کردن کسر چیست؟
ساده کردن کسر یعنی ساده کردن اعداد صورت و مخرج آن کسر تا جایی که هیچ عامل مشترکی بهجز ۱ نداشته باشند. به بیان دیگر، یک کسر زمانی سادهترین شکل خود را دارد که صورت و مخرجش نسبت به همدیگر اول باشند.
برای مثال، کسر را در نظر بگیرید. این کسر را نمیتوان بیش از این ساده کرد، چون صورت و مخرج آن عامل مشترکی غیر از یک ندارند.
توجه داشته باشید که مقدار کسر پس از ساده کردن بدون تغییر باقی میماند. این یعنی اینکه کسر سادهشده و کسر اولیه، کسرهای معادل هم هستند. در بخشهای بعدی، نحوه ساده کردن کسرها را با حل مثال توضیح میدهیم.
پیشنهاد مطالعه: بهترین روش های آموزش ریاضی به کودکان + راهنمای سنی
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
2 روش کلی ساده کردن کسر ها
ساده کردن کسر با استفاده از بزرگترین مقسوم علیه مشترک (ب م م)
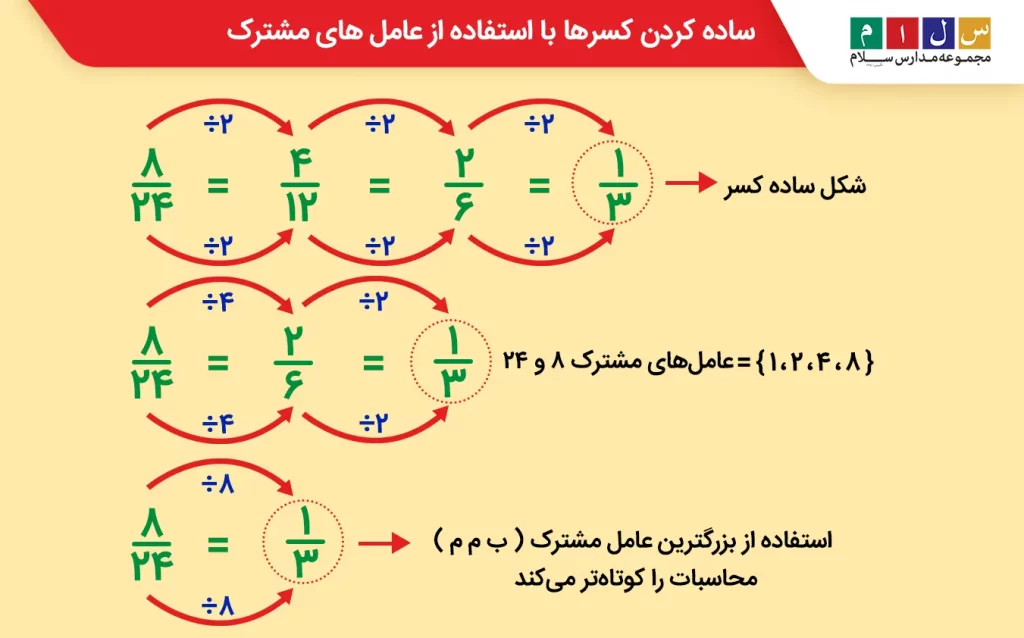
برای اینکه با فرایند سادهسازی کسرها آشنا شوید، یک مثال با هم حل میکنیم. فرض کنید میخواهیم کسر را ساده کنیم. برای این کار باید طبق مراحل زیر پیش برویم:
گام اول: عاملهای صورت و مخرج را مینویسیم. منظور از عاملها همان مقسومعلیهها است؛ یعنی اعدادی که صورت و مخرج بر آنها بخشپذیرند. عاملهای ۸ و ۲۴ عبارتاند از:
- عاملهای عدد ۸: ۱، ۲، ۴ و ۸
- عاملهای عدد ۲۴: ۱، ۲، ۳، ۴، ۶، ۸، ۱۲ و ۲۴
گام دوم: عاملهای مشترک صورت و مخرج را تعیین میکنیم. عاملهای مشترک ۸ و ۲۴ اعداد ۱، ۲، ۴ و ۸ هستند.
گام سوم: صورت و مخرج را بر بزرگترین عامل مشترک (ب م م) تقسیم میکنیم. در اینجا ب م م «۸» است. بنابراین، اگر صورت ومخرج را بر ۸ تقسیم کنیم، کسربه دست خواهد آمد. کسر
سادهترین شکل کسر
ست، زیرا عدد ۱ و ۳ نسبت به هم اول هستند و هیچ عامل مشترکی غیر از ۱ ندارند.
نکته: دقت داشته باشید که سادهسازی این کسر را میتوانستیم با عاملهای مشترک دیگر هم انجام دهیم، اما در این صورت فرایند سادهسازی و محاسبات طولانیتر خواهد شد.
تصویر زیر، این تفاوت را بهخوبی نشان میدهد.
ساده کردن کسر با استفاده از عامل های اول
روش دیگر برای ساده کردن کسرها، تجزیه صورت و مخرج به عاملهای اول است. منظور از عاملهای اول همان اعداد اول است که تنها بر یک و خودشان بخشپذیرند.
این روش سادهسازی طی مراحل زیر انجام میشود:
گام اول: ابتدا عاملهای اول صورت و مخرج را پیدا میکنیم. یعنی صورت و مخرج را بهصورت حاصلضرب اعداد اول مینویسیم.
گام دوم: عاملهای مشترک صورت و مخرج را حذف میکنیم.
گام سوم: اعداد باقیمانده در صورت و مخرج را نگه میداریم تا شکل ساده کسر را بیابیم.
در تصویر زیر، کسر را با این روش ساده کردهایم.

ساده کردن کسرهای دارای متغیر
متغیرها حروفی مانند a، b، c، x، y، z و غیره هستند که در عبارتهای ریاضی ازجمله کسرها بهعنوان مقادیر نامعلوم دیده میشوند.
کسرهایی که دارای متغیر هستند، طبق مراحل زیر ساده میشوند:
گام اول: جملههای مشابه را دستهبندی میکنیم. برای مثال، در کسر زیر جملههایی را که شامل a هستند، در یک گروه قرار میدهیم و حاصل صورت را بهدست میآوریم.
گام دوم: عاملهای مشترک را مییابیم و آنها را حذف میکنیم تا کسر ساده شود.
پیشنهاد مطالعه: آموزش تبدیل کسر به اعشار ششم
ساده کردن کسر دارای عدد توان دار
کسرهایی که شامل اعداد توان دار هستند نیز قابلیت ساده شدن دارند. برای ساده کردن چنین کسرهایی کافیست اعداد تواندار در صورت و مخرج را بهشکل گسترده بنویسیم و سپس، اعداد مشترک را حذف کنیم.
به مثال زیر توجه کنید تا بهتر متوجه شوید.
پیشنهاد مطالعه: ضرب و تقسیم اعداد توان دار + مثال
ساده کردن اعداد مخلوط
در مقاله عدد مخلوط توضیح دادیم که عدد مخلوط ترکیبی از یک عدد کامل و یک عدد کسری است. اگر بخواهیم این اعداد را ساده کنیم، تنها کافیست بخش کسری آنها را با روشهایی که معرفی کردیم، سادهسازی کنیم.
بهعنوان مثال، برای سادهسازی عدد فقط بخش کسری آن را ساده میکنیم.
بنابراین، شکل ساده بهصورت
خواهد بود.
ساده کردن کسرهای بزرگ تر از واحد
کسرهای بزرگتر از واحد کسرهایی هستند که مقدار صورتشان از مقدار مخرج بزرگتر است. فرایند ساده کردن این نوع کسرها مانند کسرهای دیگر است. تنها تفاوتی که وجود دارد این است که پس از ساده کردن کسر، با روشهایی که در مقاله تبدیل کسر به عدد مخلوط معرفی کردیم، آن را به عدد مخلوط تبدیل میکنیم. برای مثال، کسر را ابتدا بهصورت زیر ساده کرده و سپس بهشکل عدد مخلوط مینویسیم:
گاهی اوقات مقادیر صورت و مخرج یک کسر بهگونهای هستند که بهراحتی نمیتوان عاملهای آنها را تعیین کرد. راهکار مفید برای ساده کردن چنین کسرهایی، آشنایی با قواعد بخشپذیری اعداد است.
پیشنهاد میکنیم در کنار مطالعه این مقاله، سری هم به آموزش بخش پذیری اعداد بزنید. در آنجا قواعد بخشپذیری بر اعداد ۱ تا ۲۰ را بهطور مفصل بیان کردهایم.
نمونه سؤالات ساده کردن کسرها
سوال: کسرهای زیر را ساده کنید.
جواب: برای ساده کردن کسرهای دادهشده از روشهایی که در بخشهای قبل توضیح دادیم کمک میگیریم.
سخن پایانی
در این مقاله، به آموزش ساده کردن کسرها پرداختیم و دو روش کاربردی برای انجام آن معرفی کردیم. در روش اول باید صورت و مخرج کسر را بر یک عدد مشترک تقسیم کنیم. این عدد مشترک، بزرگترین عددی است که هم صورت و هم مخرج بر آن بخشپذیر هستند. روش دوم برای ساده کردن کسر، تجزیه صورت و مخرج آن به عاملهای اول است. در این روش، صورت و مخرج بهشکل حاصلضرب اعداد اول نوشته شده و سپس، عاملهای مشترک حذف میشوند.
در آخر، خوب است بدانید که در فرایند سادهسازی کسرها آشنایی با قواعد بخشپذیری کمککننده خواهد بود.









