فهرست مطالب
Toggleریاضی برای بسیاری از دانشآموزان به خصوص در مبحث هندسه همیشه چالشبرانگیز است، اما همین موضوعات اگر با توضیح درست و مثالهای کاربردی همراه شوند میتوانند شیرینی و جذابیت خاصی پیدا کنند. مثلث قائم الزاویه یکی از مهمترین اشکال هندسی است که کاربردهای گوناگون و ساختار سادهای دارد.
در این مطلب مجموعه مدارس سلام قدمبهقدم سراغ تعریف، ویژگیها، فرمولهای مهم و کاربردهای مثلث قائم الزاویه میرویم تا هر دانشآموز بتواند هم مفاهیم پایه را خوب یاد بگیرد و هم برای حل تمرینها و امتحانها دانش بیشتری داشته باشد. پس اگر میخواهید تسلط کاملی نسبت به این مثلث پرکاربرد پیدا کنید، با ما همراه باشید.
مثلث قائم الزاویه چیست؟
مثلث قائم الزاویه یکی از انواع مثلث است همانطور که از نامش مشخص است، مثلثی است که یکی از زاویههای آن دقیقاً ۹۰ درجه باشد.
ویژگیهای این مثلث، به این شرح است:
- به زاویهای که برابر با ۹۰ درجه است زاویه قائمه گفته میشود.
- ضلع روبهروی این زاویه را وتر مینامند که بلندترین ضلع مثلث است.
- دو ضلع دیگر که زاویه قائمه را تشکیل میدهند، ضلعهای قائم یا ساقهای مثلث محسوب میشوند.
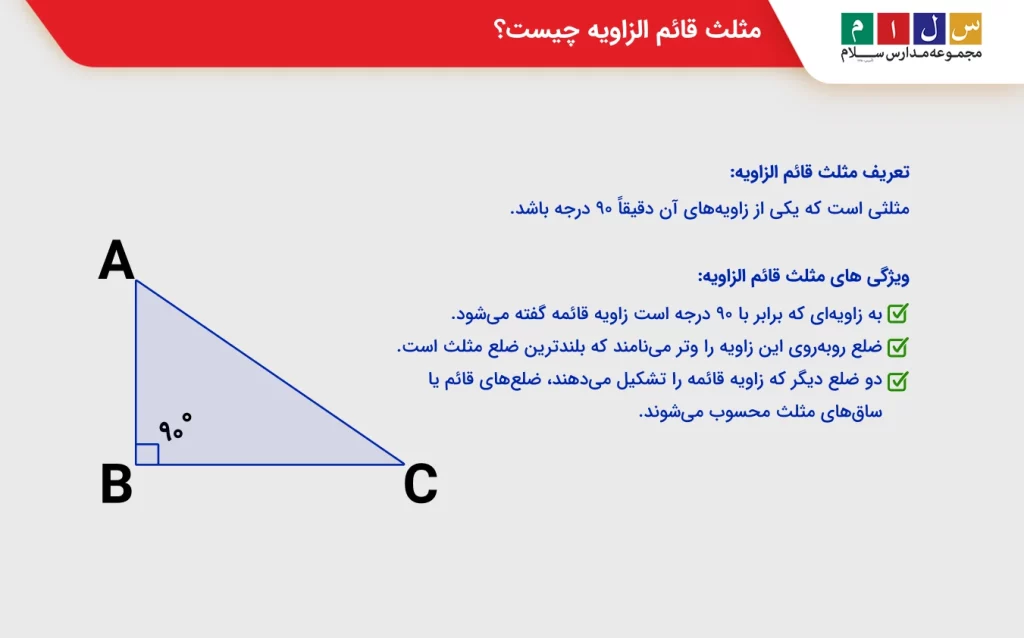
همانطور که در شکل مشخص است، یک زاویه از زوایای این مثلث، ۹۰ درجه است. از این رو یک مثلث قائم الزاویه به حساب میآید.
البته همیشه به این شکل قرار نمیگیرد و این زاویه ۹۰ درجه ممکن است مانند تصویر زیر در قسمت دیگری از شکل قرار گیرد و یا اندازه اضلاع متفاوت باشد.
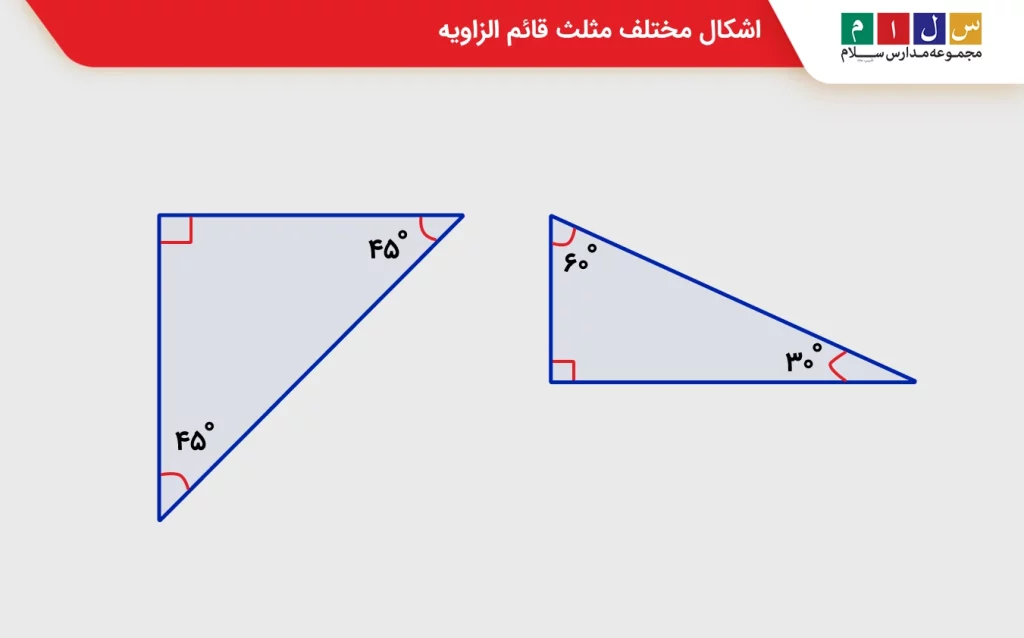
در نتیجه این تعریف مثلث قائم زاویه اگرچه ساده است، اما در مجموع دروازهای برای ورود به بسیاری از مفاهیم مهمتر مثل رابطه فیثاغورس، محاسبه مساحت و حتی درک پایهای از مثلثات است. در ادامه بهصورت جداگانه به بررسی مساحت، محیط و فرمول محاسبه مثلث قائم الزاویه خواهیم پرداخت تا به خوبی بر این مبحث و نحوه حل مسائل آن مسلط شوید.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
مساحت مثلث قائم الزاویه
برای محاسبه مساحت کافی است قاعده و ارتفاع را در هم ضرب کنیم و سپس آن را به 2 تقسیم کنیم. به زبان ساده، فرمول مساحت به شکل زیر نوشته میشود:
۲ ÷ (ارتفاع × قاعده) = مساحت مثلث قائم الزاویه
در مثلث ABC که زاویه (A) قائمه است، ضلع (AB) را قاعده و ضلع (AC) را ارتفاع در نظر میگیریم. در نتیجه:
۲ ÷ (AB x AC) = مساحت

مثال زیر را حل کنید:
قاعده = ۶
ارتفاع = ۴

۱. در ابتدا مقادیر را در فرمول میگذاریم:
۲ ÷ (۴ × ۶) = مساحت
۲. ضرب را انجام می دهیم:
۴ × ۶ = ۲۴
۳.تقسیم میکنیم و مساحت را به دست میآوریم:
۱۲ = ۲ ÷ ۲۴
پس مساحت این مثلث قائم الزاویه برابر با ۱۲ سانتیمتر مربع است.
در مطلب دیگر به بررسی کامل مساحت مثلث قائم الزاویه با روشها و مثالهای مختلف پرداختهایم.
محیط مثلث قائم الزاویه
محیط هر مثلث برابر است با جمع طول سه ضلع آن. در مثلث قائم الزاویه نیز محیط را از جمع قاعده، ارتفاع و وتر به دست میآوریم. اگر مثلثی با نام ABC داشته باشیم که در آن زاویه قائمه 90 باشد، آنگاه محیط مثلث چنین نوشته میشود:
محیط =AC+ AB + BC
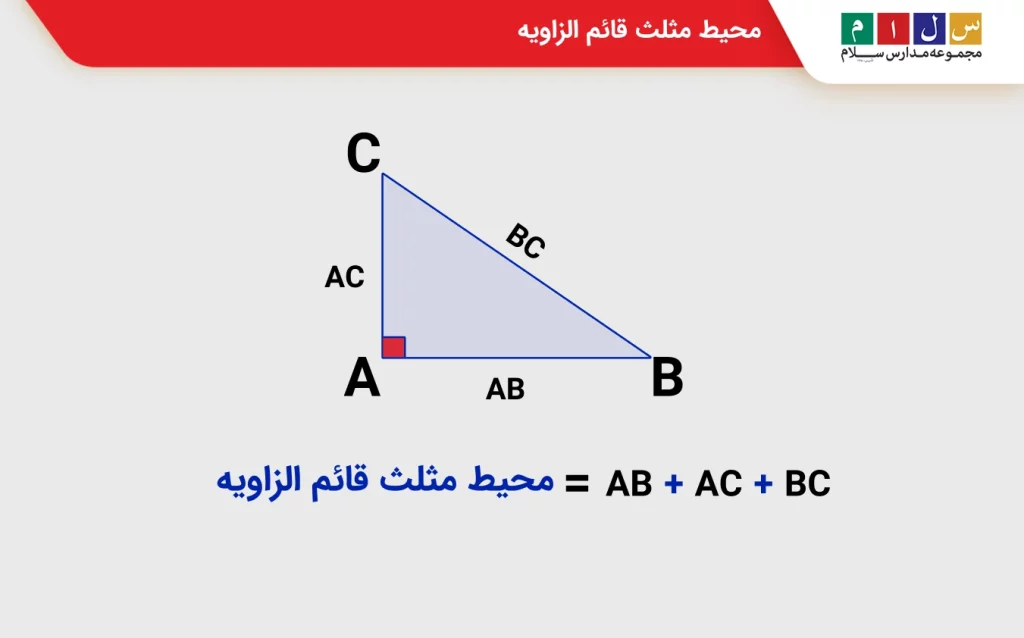
در آن (AB) و (AC) دو ضلع عمود بر هم هستند و (BC) همان وتر مثلث است.
- مثال:
فرض کنید مثلث قائمالزاویه داریم با شرایط زیر:
(AB = ۳)
(AC = ۴)
( ? = BC )
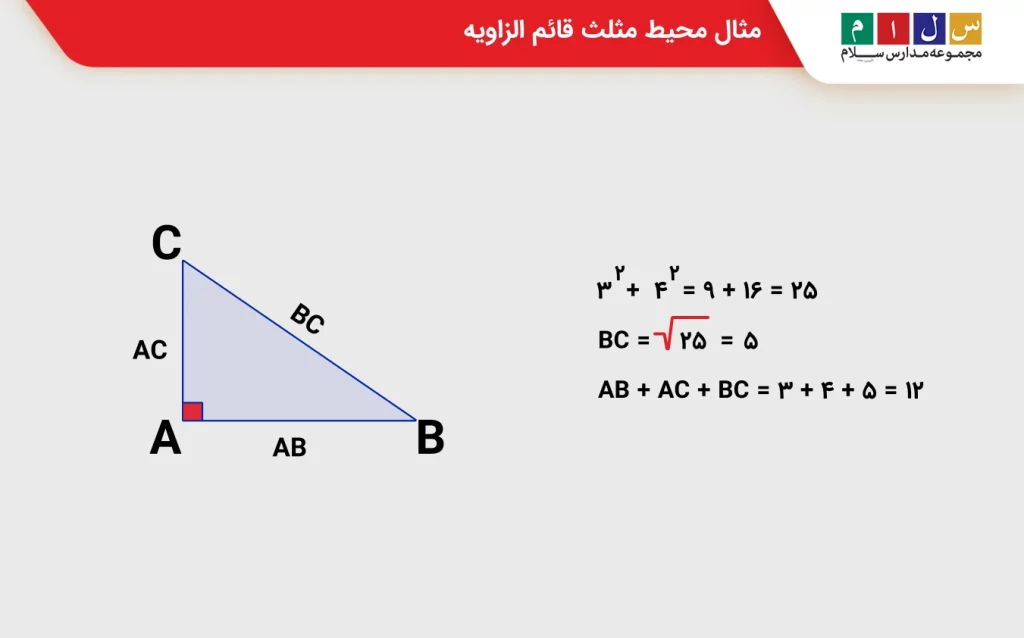
۱.ابتدا وتر را با قضیه فیثاغورس به دست میآوریم:
۳۲+ ۴۲ = ۹+۱۶ = ۲۵
۲.جذر میگیریم:
BC = ۵
۳.حالا محیط را حساب میکنیم:
محیط = AB + AC + BC = ۳ + ۴ + ۵ = ۱۲
در نتیجه محیط مثلث قائم الزاویه برابر با ۱۲ سانتیمتر است. این روش همیشه ثابت بوده و تنها باید سه ضلع را داشته باشید، آنها را با هم جمع کنید و واحد طول را در کنار جواب بنویسید.
در مقاله دیگر به بررسی کامل محیط مثلث قائم الزاویه با روشها و مثالهای مختلف پرداختهایم.
انواع مثلث قائم الزاویه
هر مثلثی که یک زاویه ۹۰ درجه داشته باشد، مثلث قایم زاویه محسوب میشود، اما بقیه زوایا و ضلعها میتوانند حالتهای متفاوتی ایجاد کنند. برهمین اساس، مثلثهای قائم الزاویه را به دو دسته اصلی تقسیم میکنند: متساوی الساقین و مختلف الاضلاع.
مثلث قائم الزاویه متساوی الساقین
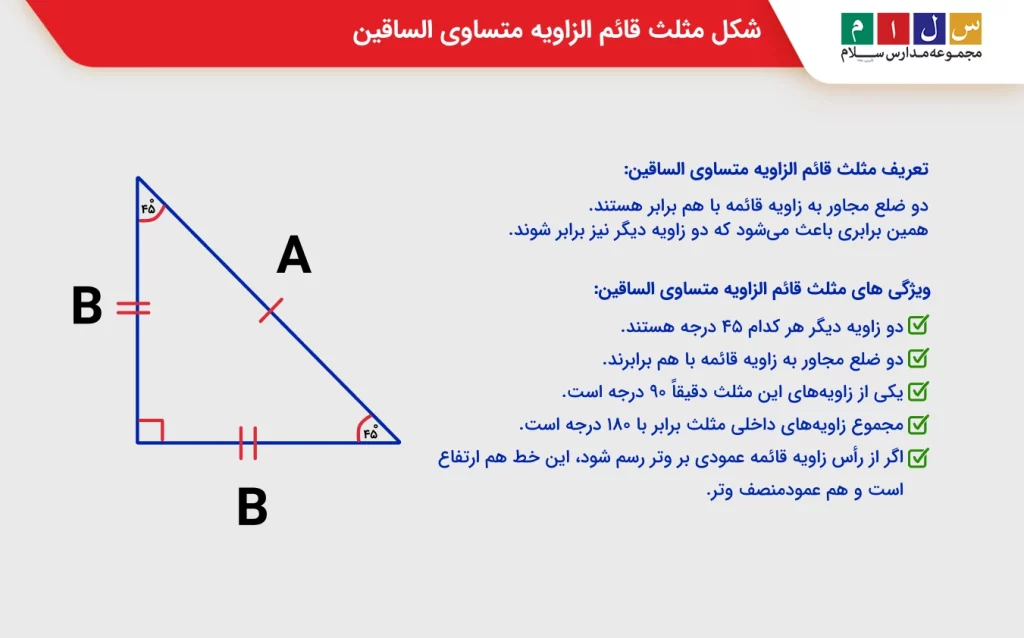
در این نوع مثلث، دو ضلع مجاور به زاویه قائمه با هم برابر هستند. همین برابری باعث میشود که دو زاویه دیگر نیز برابر شوند و هر کدام ۴۵ درجه باشند. به همین دلیل مثلث قائم الزاویه متساوی الساقین همیشه زاویههای ۹۰، ۴۵ و ۴۵ درجه دارد و نسبت اضلاع آن نیز الگوی مشخصی را دنبال میکند که در حل مسائل هندسه و مثلثات بسیار پرکاربرد است.
ویژگی های مثلث قائم الزاویه متساوی الساقین
- یکی از زاویههای این مثلث دقیقاً ۹۰ درجه است.
- دو ضلع مجاور به زاویه قائمه با هم برابرند.
- دو زاویه دیگر هر کدام ۴۵ درجه هستند.
- مجموع زاویههای داخلی مثلث برابر با ۱۸۰ درجه است.
- اگر از رأس زاویه قائمه عمودی بر وتر رسم شود، این خط هم ارتفاع است و هم عمودمنصف وتر.
محاسبه وتر مثلث قائم الزاویه متساوی الساقین
فرض کنید یک مثلث قائم الزاویه متساوی الساقین داریم که اسمش را PQR میگذاریم. زاویه (Q) قائمه است، یعنی ۹۰ درجه. دو ضلع برابر هستند، پس:
(PQ = QR = x)
وتر مثلث یعنی ضلع روبهروی زاویه قائمه، (PR) است و میخواهیم آن را حساب کنیم.

حالا مرحله به مرحله حساب میکنیم:
فرمول فیثاغورس میگوید:
۲ ضلع + ۲ضلع قائم = ۲وتر
بر این اساس، مقدارها را جایگذاری میکنیم:
PR۲ = PQ۲ + QR۲
l۲ = x۲ + x۲
حالا بر این اساس، اضلاع را جمع میکنیم:
l۲ = ۲x۲
پس جذر میگیریم و پاسخ میشود:
l = x√۲
در نتیجه طول وتر مثلث همیشه برابر است با طول هر ضلع ضربدر ریشه دو.
مثلث قائم الزاویه مختلف الاضلاع
در این نوع مثلث، سه ضلع طولهای متفاوتی دارند و در نتیجه دو زاویه تیز هم مقدارهای نابرابر خواهند داشت. یکی از حالتهای مهم این دسته، مثلث ۳۰-۶۰-۹۰ میباشد که در آن طول وتر همیشه دو برابر کوتاهترین ضلع و ضلع سوم برابر با ریشه سه برابر آن ضلع کوچکتر است.
مثلث قائم الزاویه در مثلثات
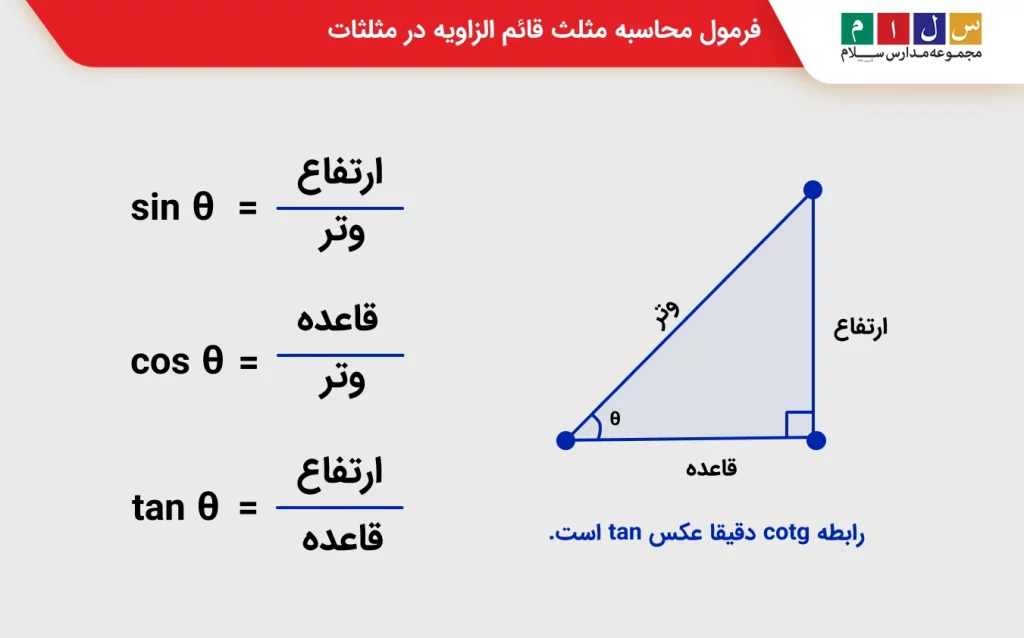
در مثلثات همیشه نقطه شروع یک مثلث قائم زاویه است، یعنی مثلثی که یکی از زاویههای آن دقیقاً ۹۰ درجه باشد. برای اینکه نسبتها و فرمولهای مثلثاتی را بهتر بشناسیم، ضلعها را نامگذاری میکنیم:
- وتر: بلندترین ضلع مثلث که روبهروی زاویه ۹۰ درجه قرار دارد.
- ضلع روبهرو: ضلعی که روبهروی زاویه θ قرار دارد.
- ضلع مجاور: ضلعی که در کنار زاویه θ است و با آن زاویه ساخته میشود.
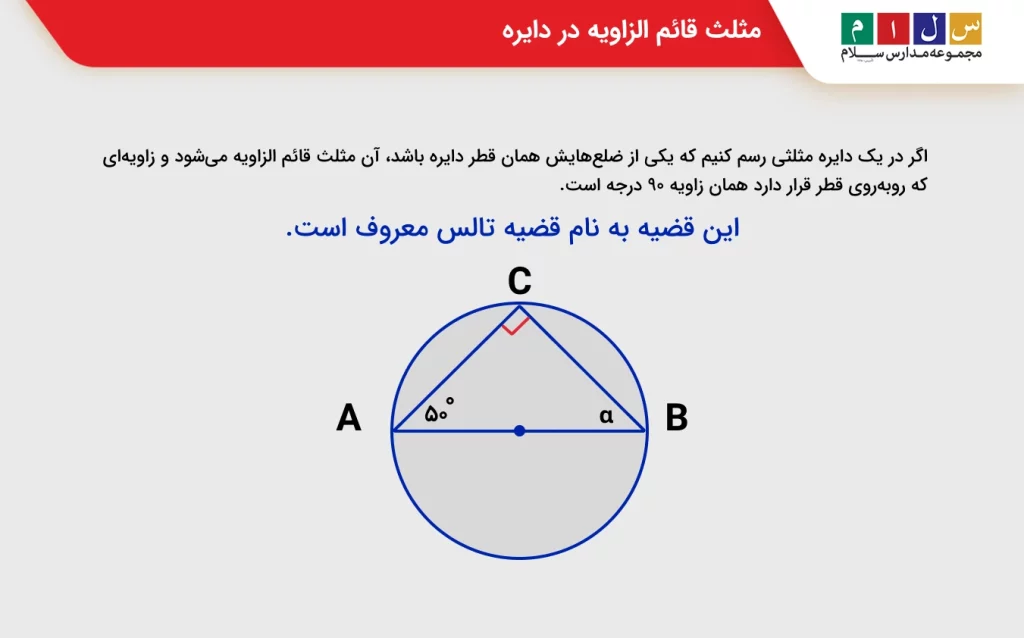
مثلث قائم الزاویه در دایره
وقتی یک دایره داریم و یک مثلث داخل آن رسم میکنیم (یعنی هر سه رأس مثلث روی محیط دایره قرار بگیرد)، اگر یکی از زاویههای این مثلث قائم باشد، یک نکته خیلی مهم اتفاق میافتد:
- وتر مثلث قائم الزاویه همان قطر دایره است.
برعکسش هم درست است:
- اگر در یک دایره مثلثی رسم کنیم که یکی از ضلعهایش همان قطر دایره باشد، آن مثلث قائم الزاویه میشود و زاویهای که روبهروی قطر قرار دارد همان زاویه ۹۰ درجه است.
این قضیه به نام قضیه تالس معروف است.
فرمول محاسبه اضلاع مثلث قائم الزاویه
برای محاسبه مثلث قائم الزاویه، از روابط مثلثاتی ذکر شده در بالا و یا از رابطه فیثاغورس استفاده میشود. به عبارتی دیگر، این فرمول به اضلاع دادهشده و صورت مسئله بستگی دارد. علاوه بر این، خوب است بدانید که در میان اضلاع مثلث، این روابط برقرار است:
c۲ = a۲ + b۲
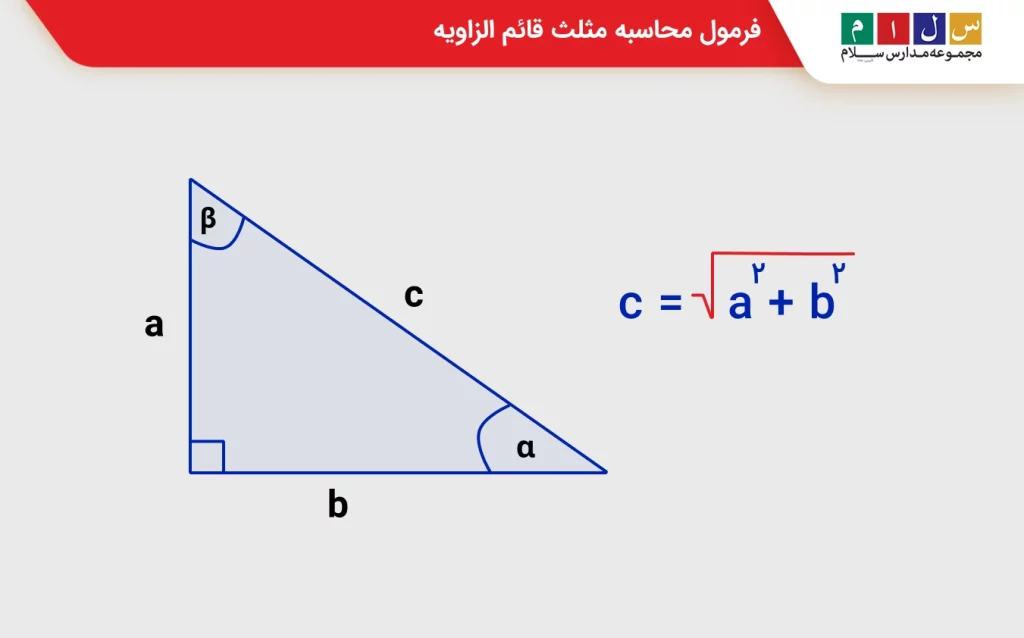
محاسبه اضلاع مثلث قائم الزاویه با زاویه
در اولین مرحله باید فرمولها را مشخص کنیم:

سپس بر اساس ضلع و قسمتهایی که داریم، از یکی از این سه فرمول برای به دست آوردن پاسخ استفاده میکنیم.
رابطه فیثاغورس در مثلث قائم الزاویه
همانطور که اشاره کردیم، رابطه فیثاغورس برای محاسبه مثلث قائم الزاویه و به خصوص محاسبه طول وتر استفاده میشود. نگران اسم دشوار و عجیب آن نباشید، رابطهای ساده دارد که به آسانی از طریق آن اضلاع به دست میآیند.
در واقع رابطه فیثاغورس یکی از اصلیترین قانونهای ریاضی در مثلثات است که ارتباط مستقیم بین سه ضلع مثلث قائم الزاویه را نشان میدهد. بر اساس این قضیه، اگر دو ضلع عمود بر هم مثلث را (a) و (b) در نظر بگیریم و وتر آن را (c) بنامیم، همیشه داریم:

محاسبه اضلاع مثلث قائم الزاویه با وتر
۱.در ابتدا نامگذاری را به همان شکل که در مثالهای قبلی گفته شد، انجام دهید:
نامگذاری: ضلع روبهرو، ضلع مجاور، وتر
۲.سپس بر اساس ضلعی که داریم و ضلعی که میخواهیم، از روابط مثلثاتی کمک میگیریم:

بر این اساس، تنها باید اضلاع داده شده را جایگذاری کنید تا جواب را با فرمول به دست آورید.
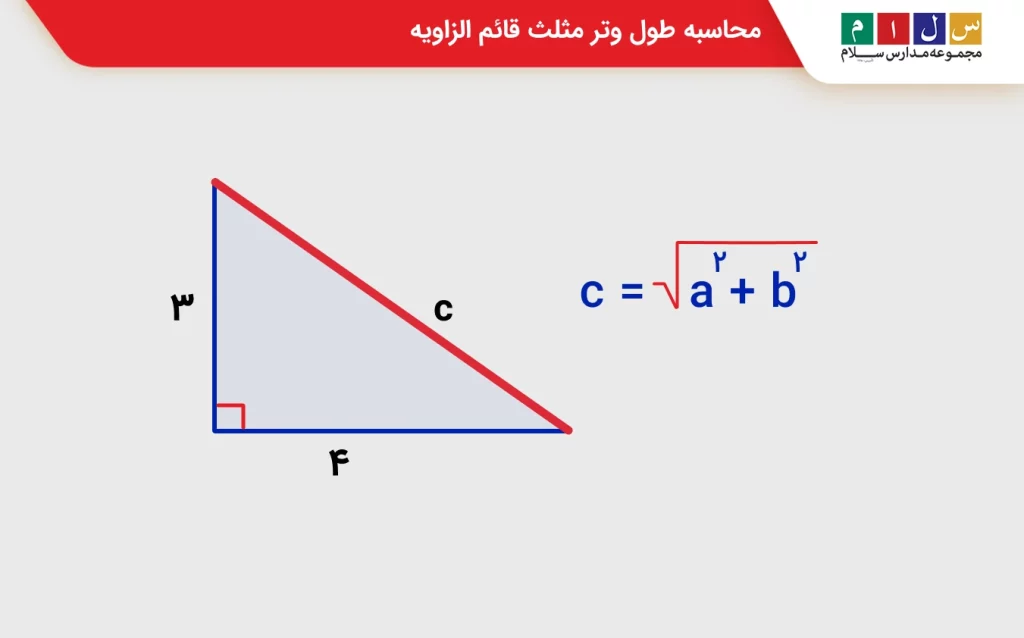
محاسبه طول وتر مثلث قائم الزاویه
برای محاسبه طول وتر مثلث قائم الزاویه از قضیه فیثاغورس کمک میگیریم که به این شرح است:

تنها باید ضلع یک و ضلع دو را در قسمت a و b جایگذاری کرده و پس از جذر و رادیکال گرفتن، وتر را به دست آورید. در قسمت تمرین، مثال تمامی موارد را خواهیم آورد.
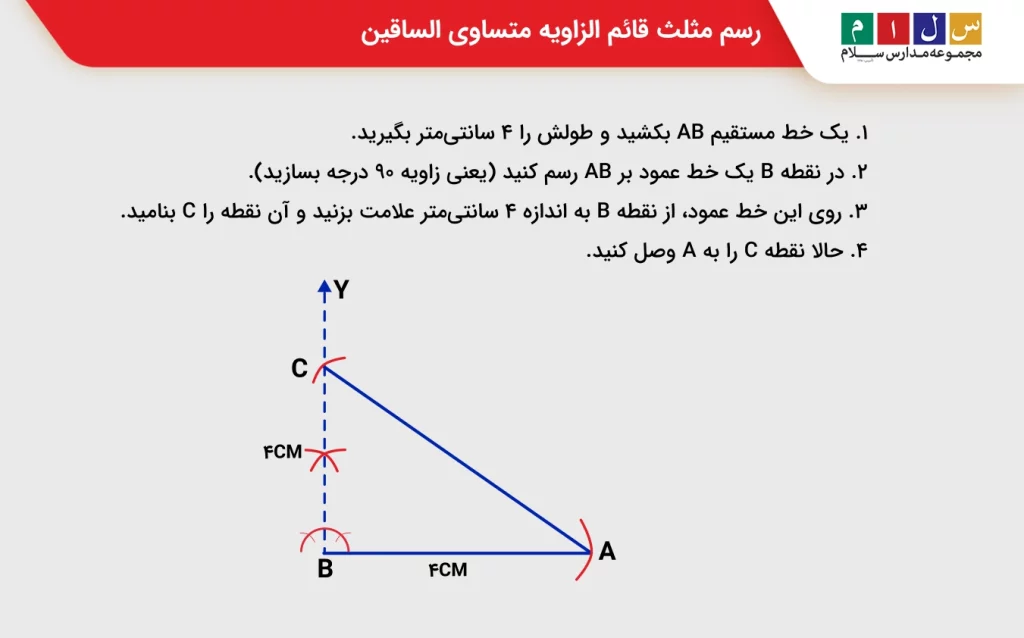
رسم مثلث قائم الزاویه متساوی الساقین
برای مثال فرض کنید که برای رسم مثلث قائم الزاویه متساوی الساقین صورت مسئله گفته که یک ضلع باید 4 باشد و یا خودتان ضلع اولی را 4 سانتیمتر در نظر بگیرید. به این ترتیب با مراحل ساده زیر میتوانید رسم را انجام دهید:
- یک خط مستقیم AB بکشید و طولش را ۴ سانتیمتر بگیرید.
- در نقطه B یک خط عمود بر AB رسم کنید (یعنی زاویه ۹۰ درجه بسازید).
- روی این خط عمود، از نقطه B به اندازه ۴ سانتیمتر علامت بزنید و آن نقطه را C بنامید.
- حالا نقطه C را به A وصل کنید.
تمرین مثلث قائم الزاویه
تمرین اول:
یک مثلث قائم الزاویه داریم که طول دو ضلع عمود بر هم (قاعده و ارتفاع) به ترتیب ۵ سانتیمتر و ۷ سانتیمتر است. مساحت این مثلث را به دست آورید.

فرمول مساحت مثلث قائم زاویه را در نظر میگیریم:
۲ ÷ (ارتفاع × قاعده) = مساحت
جایگذاری میکنیم:
(۷×۵) ÷ ۲ = ۱۷.۵
تمرین دوم:
در یک مثلث قائم الزاویه، طول دو ضلع مجاور به زاویه قائمه به ترتیب برابر ۵ و ۱۲ واحد است. برای به دست آوردن طول وتر از قضیه فیثاغورس استفاده میکنیم:
c۲ = a۲ + b۲
c۲ = ۱۲۲ + ۵۲
c۲ = ۱۴۴ +۲۵
c۲ = ۱۶۹
c = ۱۳
در نتیجه طول وتر این مثلث برابر ۱۳ واحد خواهد بود.
تمرین سوم:
یک مثلث قائم الزاویه با یک زاویه ۳۰ درجه داریم و طول وتر برابر ۱۰ واحد داده شده. میخواهیم ضلع مقابل زاویه ۳۰ درجه را حساب کنیم.
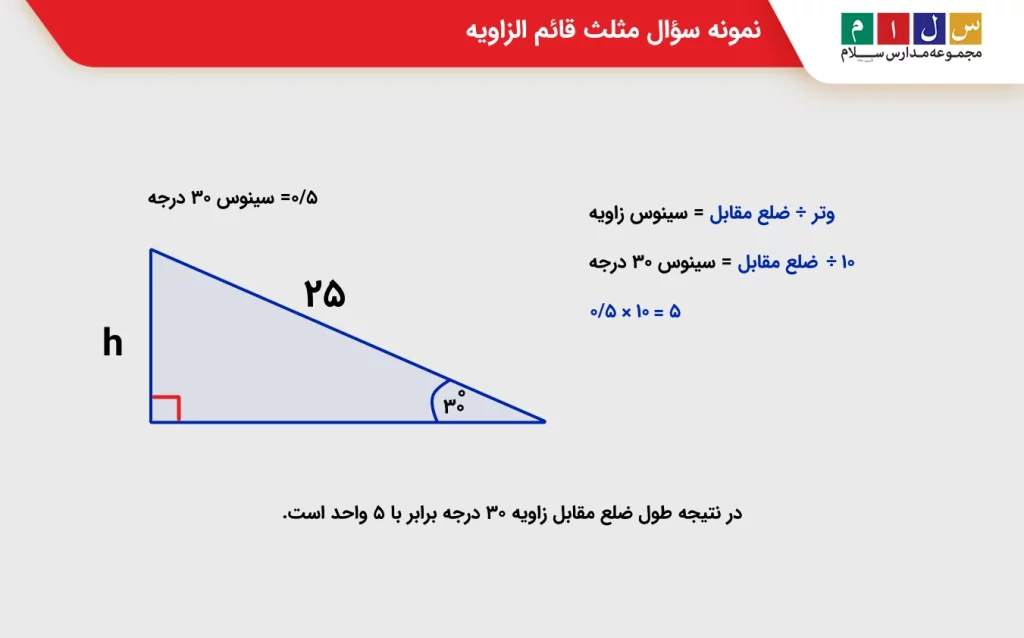
برای حل این مسئله میتوانیم از روابط مثلثاتی و فرمول سینوس استفاده کنیم.
وتر÷ ضلع مقابل = سینوس زاویه
۱۰ ÷ ضلع مقابل = سینوس ۳۰ درجه
میدانیم سینوس ۳۰ درجه برابر با ۰/۵ است، پس:
۰/۵ = ۱۰ ÷ ضلع مقابل
حالا هر دو طرف معادله را در ۱۰ ضرب میکنیم:
۱۰ × ۰/۵ = ۵
در نتیجه طول ضلع مقابل زاویه ۳۰ درجه برابر با ۵ واحد است.
سخن پایانی
مثلث قائم الزاویه یکی از اشکال هندسی ساده است که به راحتی میتوانید مساحت و محیط آن را به دست آورید. اغلب فرمولها و مسائل پیچیدهتر این مثلث هم تنها با به خاطر سپردن فرمولهای مختصری مثل قضیه فیثاغورس ممکن هستند. برای اینکه در ذهنتان بماند، به مثالها و تمرینهای این مطلب دقت کنید.
سؤالات متداول
- آیا یک مثلث میتواند هم متساوی الاضلاع باشد هم قائم الزاویه چرا؟
خیر، چون در مثلث متساوی الاضلاع همه زاویهها ۶۰ درجه هستند و هیچ زاویه قائمهای وجود ندارد. - آیا یک مثلث میتواند هم قائم الزاویه باشد هم متساوی الساقین؟
بله، اگر دو ضلع مجاور زاویه قائمه برابر باشند، مثلث قائم الزاویه متساوی الساقین ساخته میشود. - مثلث قائم الزاویه با زاویه باز وجود ندارد؟
خیر، چون در مثلث قائم الزاویه یک زاویه ۹۰ درجه است و مجموع زاویههای دیگر فقط ۹۰ درجه باقی میماند و هیچ زاویهای نمیتواند باز باشد.