چند ضلعی منتظم چیست؟ ׀ تعریف و ویژگی ها به زبان ساده

دیدن نظم در جهان هستی همواره انسان را به وجد می‌‌آورد، خواه در یک شکل ساده باشد خواه در کهکشان‌‌ها و اجرام آسمانی. در هندسه نیز اشکالی با ظاهر منظم وجود دارند که اضلاع و رأس‌‌های آن از نظم خاصی پیروی می‌‌کنند به‌‌گونه‌‌ای که در نگاه اول می‌‌توان متوجه آن شد. چندضلعی‌‌های منتظم اشکالی از این دست هستند که قرار است در این مطلب به آن‌‌ها بپردازیم.

در این آموزش، ابتدا با تعریف مختصری به شما توضیح خواهیم داد که چند ضلعی منتظم چیست سپس انواع این چندضلعی‌‌ها را معرفی می‌‌کنیم و فرمول‌‌های هندسی مربوط به آن‌‌ها را در اختیارتان خواهیم گذاشت. پیشنهاد می‌کنم مقاله انواع اشکال هندسی را نیز مطالعه کنید.

تعریف چند ضلعی منتظم

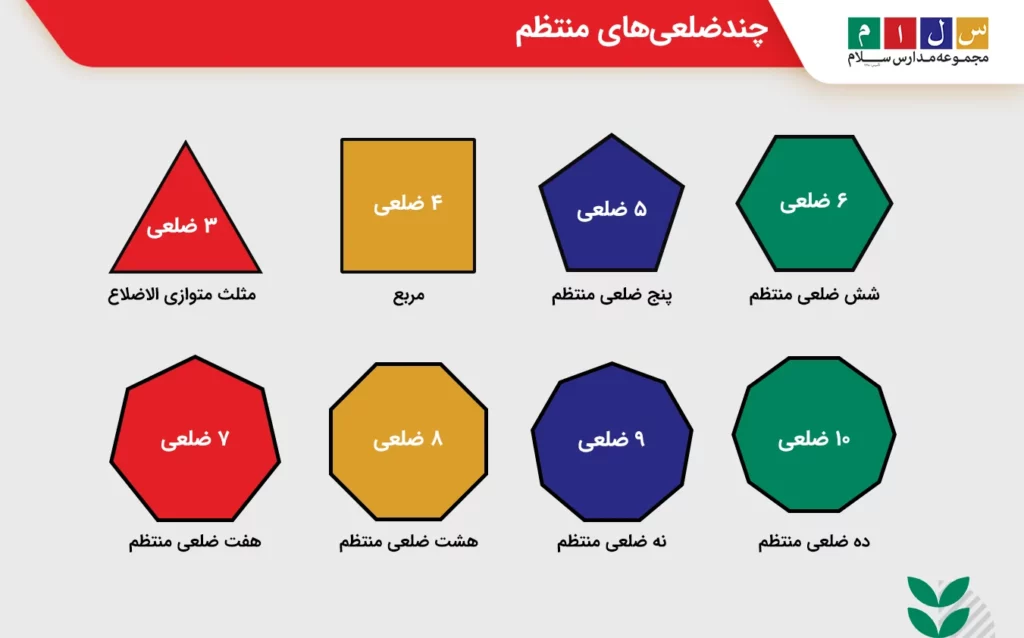
چندضلعی یک شکل مسطح و بسته است که از تعدادی خط راست ساخته می‌‌شود. این خطوط راست را ضلع و محل برخوردشان را گوشه یا رأس چندضلعی می‌‌نامند. زمانی که در یک چندضلعی اندازه اضلاع با هم و اندازه زاویه‌‌ها نیز با هم برابر باشند، آن چندضلعی منتظم خواهد بود.

به‌‌عنوان مثال، مثلث متساوی الاضلاع یک سه‌‌ضلعی منتظم و مربع نیز یک چهارضلعی منتظم است زیرا مثلث متساوی‌‌الاضلاع دارای سه ضلع برابر و سه زاویه ۶۰ درجه است و مربع نیز چهار ضلع برابر و چهار زاویه ۹۰ درجه دارد.

اجزای یک چند ضلعی منتظم

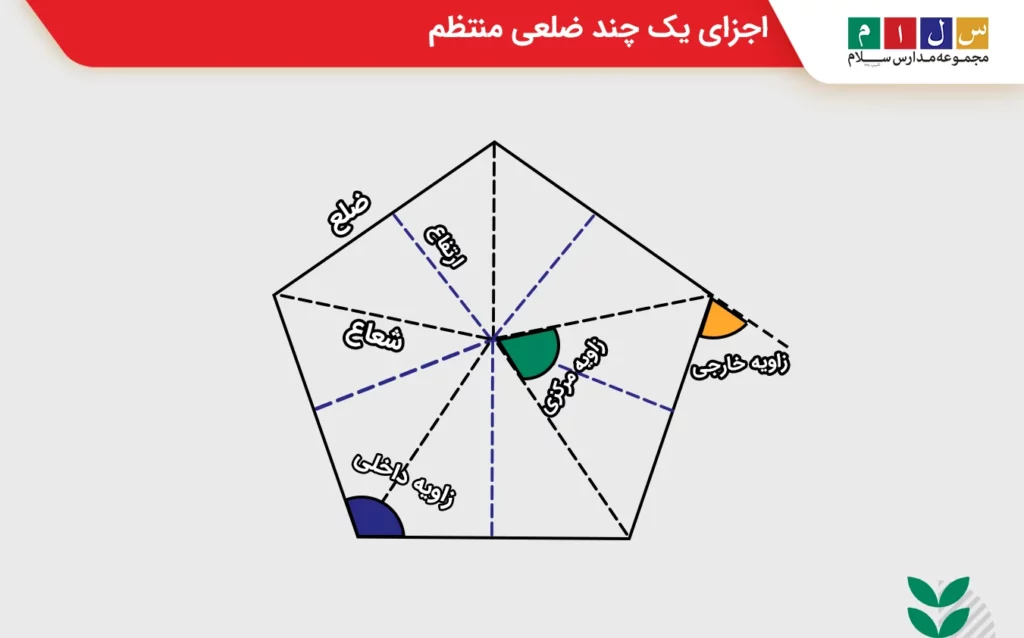
چندضلعی‌‌های منتظم از اجزای مختلفی ساخته شده‌‌اند که دانستن نام هر یک از آن‌‌ها برای فهم و درک مطالبی که در ادامه بیان می‌‌کنیم لازم است. این اجزا عبارت‌‌اند از:

• زاویه داخلی
• زاویه خارجی
• زاویه مرکزی
• ضلع
• ارتفاع
• شعاع

برای آشنایی با موقعیت هر کدام از این اجزا، آن‌‌ها را برای یک پنج ضلعی در تصویر زیر مشخص کرده‌‌ایم.

پیشنهاد مطالعه: زاویه چیست؟

مجموع زوایای داخلی چند ضلعی منتظم

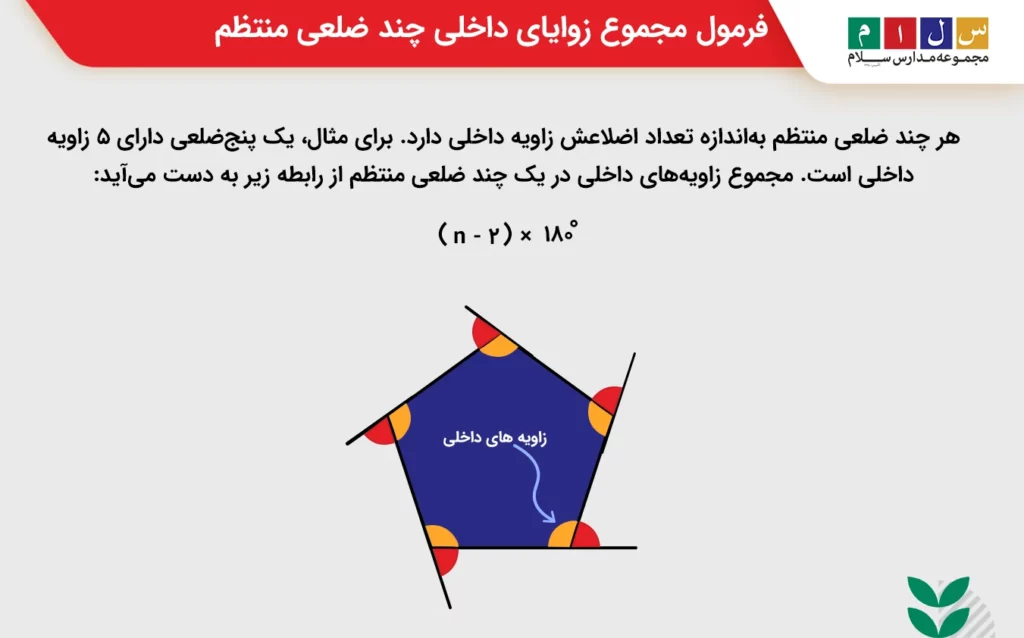
هر چند ضلعی منتظم به‌‌اندازه تعداد اضلاعش زاویه داخلی دارد. برای مثال، یک پنج‌‌ضلعی دارای ۵ زاویه داخلی است. مجموع زاویه‌‌های داخلی در یک چند ضلعی منتظم از رابطه زیر به دست می‌‌آید:

در اینجا n تعداد اضلاع است.

به‌‌عنوان مثال، در یک مربع که دارای چهار ضلع است، n=۴ است و مجموع زوایای داخلی به‌‌صورت زیر محاسبه می‌‌شود:

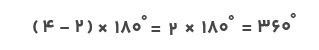
جواب حاصل نشان می‌‌دهد که مجموع زوایای داخلی مربع ۳۶۰ درجه است.

مثال: مجموع زاویه‌‌های داخلی یک هفت‌‌ضلعی منتظم ۹۰۰ درجه است. اندازه هر یک از زوایای داخلی این چندضلعی چقدر است؟

پاسخ: مجموع زوایای داخلی را داریم. ازطرفی می‌‌دانیم تعداد اضلاع برابر با ۷ است. پس با تقسیم مجموع زاویه‌‌های داخلی بر تعداد اضلاع که برابر با تعداد زوایای داخلی است می‌‌توانیم اندازه یک زاویه داخلی را محاسبه کنیم. به‌‌این‌‌ترتیب، خواهیم داشت:

بنابراین، در یک هفت‌‌ضلعی منتظم اندازه هر زاویه داخلی تقریباً مساوی است با ۱۲۸/۵۷ درجه.

مجموع زوایای خارجی چند ضلعی منتظم

برخلاف مجموع زاویه‌‌های داخلی، مجموع زوایای خارجی در همه چندضلعی‌‌های منتظم برابر با مقدار ثابت ۳۶۰ درجه است. با توجه به اینکه در یک چند ضلعی منتظم اندازه تمام زاویه‌‌های خارجی با هم مساوی است می‌‌توانیم با تقسیم این مقدار یعنی ۳۶۰ درجه بر تعداد ضلع‌‌ها مقدار هر زاویه خارجی را تعیین کنیم.

نکته ۱: هر nضلعی منتظم n زاویه خارجی برابر دارد.
نکته ۲: در چند ضلعی منتظم زاویه داخلی و زاویه خارجی مجاور آن مکمل یکدیگرند و مجموعشان مساوی ۱۸۰ درجه است.

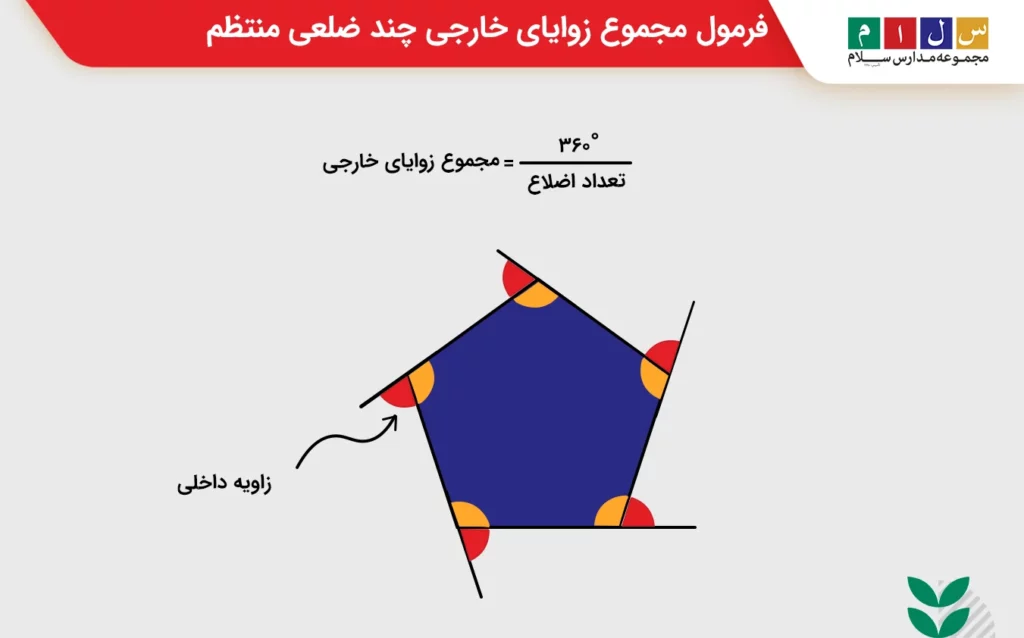
مثال: اندازه زاویه خارجی یک شش ضلعی منتظم را به دست آورید.
پاسخ: یک شش‌‌ضلعی از ۶ ضلع تشکیل شده است. اگر ۳۶۰ را بر ۶ تقسیم کنیم مقدار هر زاویه خارجی به دست می‌‌آید. داریم:

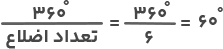
س اندازه هر زاویه خارجی شش‌‌ضلعی منتظم ۶۰ درجه است.

زاویه مرکزی چند ضلعی منتظم

زاویه مرکزی یکی دیگر از انواع زاویه در چندضلعی‌‌های منتظم است و به زاویه بین دو شعاع مجاور آن گفته می‌‌شود. مجموع زوایای مرکزی یک دایره برابر با ۳۶۰ درجه است. ازآنجا که یک n ضلعی منتظم n زاویه مرکزی برابر دارد، می‌‌توان با استفاده از رابطه زیر اندازه هر کدام از آن‌‌ها را حساب کرد. این رابطه به‌‌صورت زیر است:

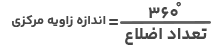
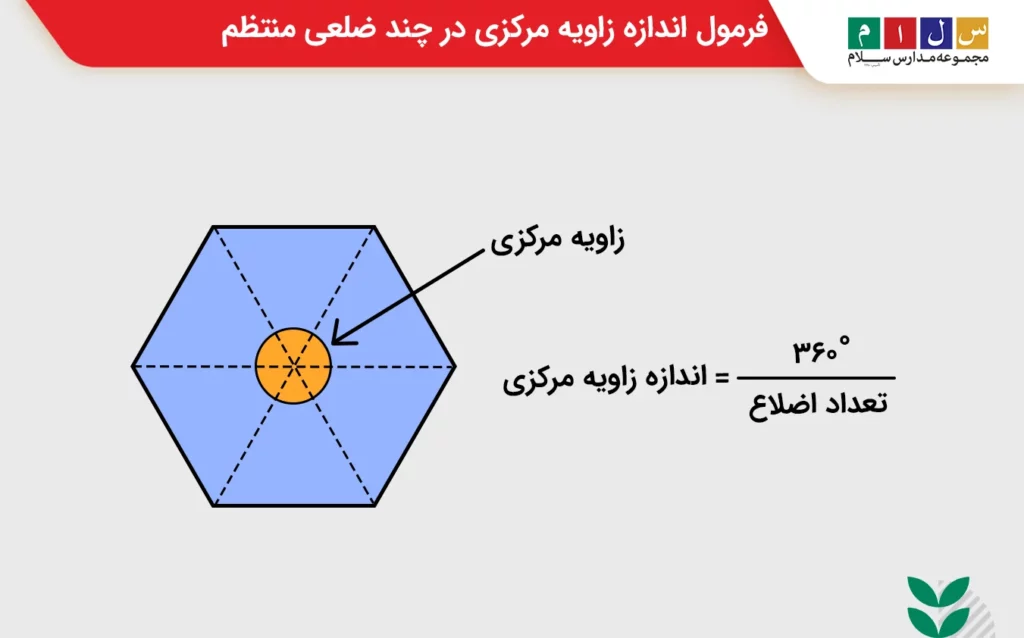
مثال: یک هشت‌‌ضلعی منتظم چند زاویه مرکزی دارد و اندازه هر یک از آن‌‌ها چقدر است؟
پاسخ: تعداد اضلاع و تعداد زاویه‌‌های مرکزی در هشت‌‌ضلعی منتظم برابر با ۸ است. بنابراین اندازه هر کدام از آن‌‌ها را می‌‌توانیم از فرمول بالا به‌‌صورت زیر به دست آوریم:

فرمول تعداد قطرها در چند ضلعی منتظم

قطر چند ضلعی منتظم به پاره‌‌خطی گفته می‌‌شود که دو رأس غیرمجاور آن را به هم وصل می‌‌کند. به‌‌طور کلی، از هر رأس یک n ضلعی منتظم می‌‌توان به تعداد n-۳ قطر رسم کرد. تصویر زیر این موضوع را به‌‌خوبی نشان می‌‌دهد.

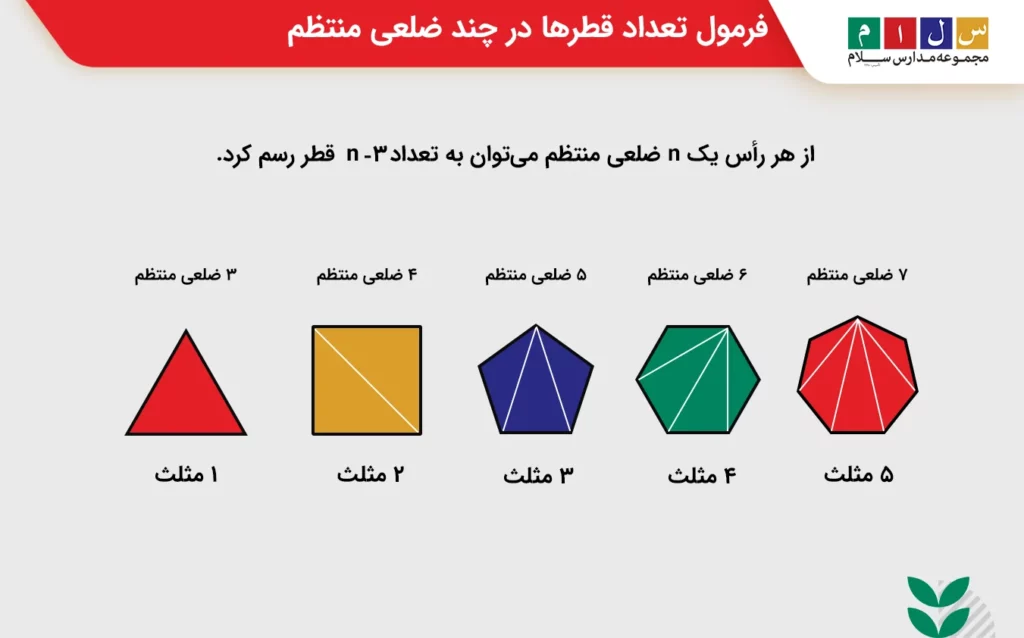
تعداد قطرهای یک چند ضلعی منتظم از فرمول زیر محاسبه می‌‌شود:

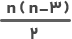
تعداد ضلع‌‌های چند ضلعی منتظم است.
برای مثال، یک شش‌‌ضلعی منتظم را در نظر بگیرید. تعداد قطرهای این چندضلعی به‌‌صورت زیر به دست می‌‌آید:

پاسخ به‌‌دست‌‌آمده نشان می‌‌دهد که یک شش‌‌ضلعی منتظم تنها ۹ قطر دارد. در شکل زیر، تمام قطرهای این چندضلعی با رنگ آبی رسم شده‌‌اند.

مرکز تقارن و محور تقارن چند ضلعی منتظم

اگر یک شکل پس از دوران ۱۸۰ درجه حول یک نقطه مرکزی دوباره روی خودش منطبق شود، می‌‌گوییم شکل تقارن مرکزی دارد. در این صورت، نقطه مرکزی را مرکز تقارن می‌‌نامیم. برای تشخیص وجود مرکز تقارن در یک چند ضلعی منتظم کافی‌‌ست فاصله هر نقطه روی محیط شکل از مرکز آن برابر با فاصله مرکز تا نقطه مقابل آن باشد.
براساس این تعریف، تنها چندضلعی‌‌های منتظمی که تعداد اضلاعشان زوج است مرکز تقارن دارند و آن‌‌هایی که تعداد اضلاعشان فرد است دارای مرکز تقارن نیستند.

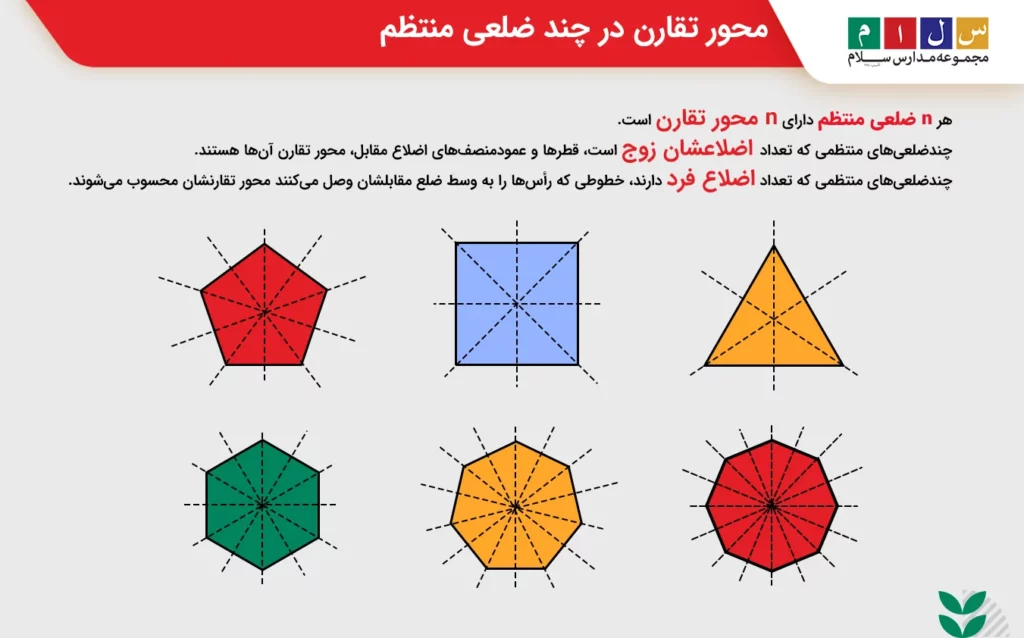
همه چندضلعی‌‌های منتظم تقارن محوری دارند، زیرا برای تمام آن‌‌ها می‌‌توان خطی فرضی در نظر گرفت که این چندضلعی‌‌ها را به دو نیمه دقیقاً مشابه تقسیم می‌‌کند. اگر چندضلعی‌‌ها را از این خط تا کنیم، دو نیمه روی هم منطبق می‌‌شوند. این خط فرضی را محور تقارن می‌‌گویند.

هر n ضلعی منتظم دارای n محور تقارن است. چندضلعی‌‌های منتظمی که تعداد اضلاعشان زوج است، قطرها و عمودمنصف‌‌های اضلاع مقابل، محور تقارن آن‌‌ها هستند و چندضلعی‌‌های منتظمی که تعداد اضلاع فرد دارند، خطوطی که رأس‌‌ها را به وسط ضلع مقابلشان وصل می‌‌کنند محور تقارنشان محسوب می‌‌شوند.

تقارن چرخشی در چند ضلعی منتظم

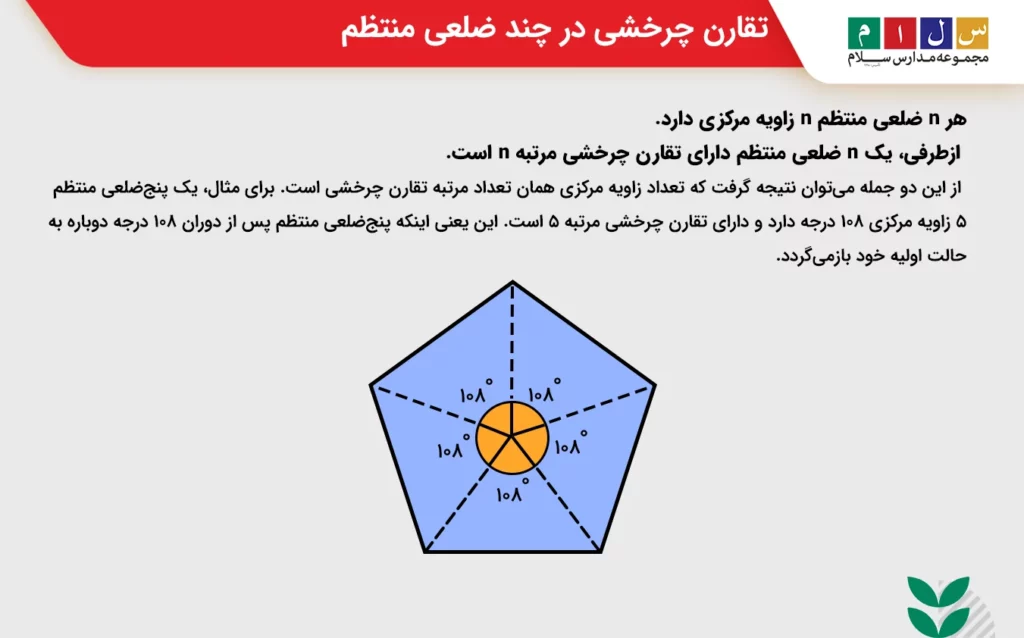
هر n ضلعی منتظم دارای تقارن چرخشی مرتبه n است. مثلاً یک مثلث تقارن چرخشی مرتبه سه و یک پنج‌‌ضلعی تقارن چرخشی مرتبه پنج دارد. تقارن چرخشی یعنی به حالت اولیه بازگشتن یک شکل پس از چرخش به‌‌اندازه معین (۱۸۰ درجه یا کمتر). طبق این تعریف می‌‌توان نتیجه گرفت که یک چند ضلعی منتظم پس از چرخش به‌‌اندازه زاویه مرکزی‌‌اش به حالت اول خود برمی‌‌گردد.

همان‌‌طور که قبلاً هم گفتیم هر n ضلعی منتظم n زاویه مرکزی دارد. ازطرفی، یک n ضلعی منتظم دارای تقارن چرخشی مرتبه n است. از این دو جمله می‌‌توان نتیجه گرفت که تعداد زاویه مرکزی همان تعداد مرتبه تقارن چرخشی است. برای مثال، یک پنج‌‌ضلعی منتظم ۵ زاویه مرکزی ۱۰۸ درجه دارد و دارای تقارن چرخشی مرتبه ۵ است. این یعنی اینکه پنج‌‌ضلعی منتظم پس از دوران ۱۰۸ درجه دوباره به حالت اولیه خود بازمی‌‌گردد.

محیط چند ضلعی منتظم

محیط چند ضلعی منتظم از مجموع طول اضلاع آن به دست می‌‌آید. ازآنجا که طول اضلاع یک چند ضلعی منتظم با هم برابر است، می‌‌توان رابطه زیر را برای تعیین محیط آن تعریف کرد:

P=na

• P: محیط چند ضلعی منتظم
• n: تعداد اضلاع 
• a: طول یک ضلع

مثال: اندازه هر ضلع یک نه‌‌ضلعی منتظم ۱۷ سانتی‌‌متر است. محیط این چندضلعی را تعیین کنید.
پاسخ: محیط نه‌‌ضلعی منتظم را به‌‌صورت زیر محاسبه می‌‌کنیم:

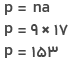
محیط نه‌‌ضلعی منتظم برابر با ۱۵۳ سانتی‌‌متر است.

مساحت چند ضلعی منتظم

مساحت چند ضلعی منتظم با استفاده از ضلع (یا محیط) و ارتفاع آن به‌‌راحتی قابل محاسبه است. فرمول کلی مساحت چند ضلعی منتظم به‌‌صورت زیر نوشته می‌‌شود:

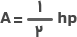
• A: مساحت چند ضلعی منتظم
• P: محیط چند ضلعی منتظم
• h: ارتفاع چند ضلعی منتظم

مثال: مساحت ده‌‌ضلعی منتظمی را به دست آورید که ضلع آن ۳ سانتی‌‌متر و ارتفاع آن ۷ سانتی‌‌متر است.
پاسخ: ابتدا محیط ده‌‌ضلعی را حساب می‌‌کنیم:

حالا با داشتن محیط و ارتفاع ده‌‌ضلعی می‌‌توانیم مساحت آن را به دست آوریم:

به‌‌این‌‌ترتیب، مساحت ده‌‌ضلعی مساوی است با ۱۰۵ سانتی‌‌متر مربع.

انواع چند ضلعی منتظم

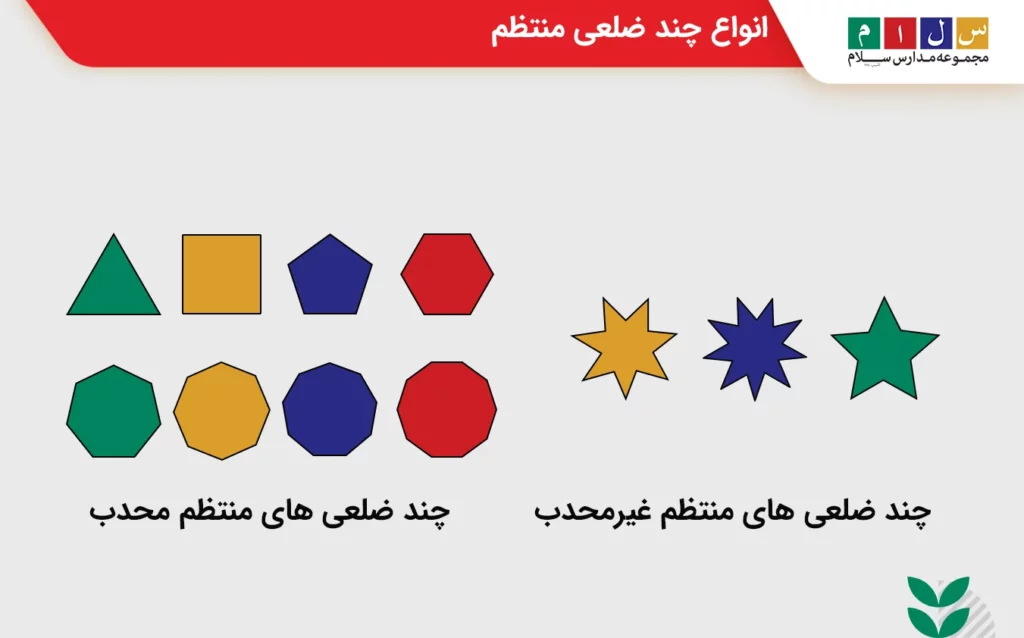
چندضلعی‌‌های منتظم می‌‌توانند محدب یا به‌‌صورت ستاره باشند. اگر در یک چند ضلعی منتظم اندازه تمام زاویه‌‌های داخلی کمتر از ۱۸۰ درجه باشد، آن را محدب می‌‌نامیم. اشکال ستاره‌‌ای نیز یکی دیگر از انواع چند ضلعی منتظم هستند. این اشکال برعکس چندضلعی‌‌های منتظم محدب، غیرمحدب‌‌اند زیرا برخی از زوایای آن اندازه‌‌ای بیشتر از ۱۸۰ درجه دارند. تصویر زیر تفاوت این دو نوع چند ضلعی منتظم را به‌‌خوبی نشان می‌‌دهد.

نکته: تمام فرمول‌‌های این آموزش برای چندضلعی‌‌های منتظم محدب بیان شدند.

چند ضلعی غیر منتظم چیست ؟

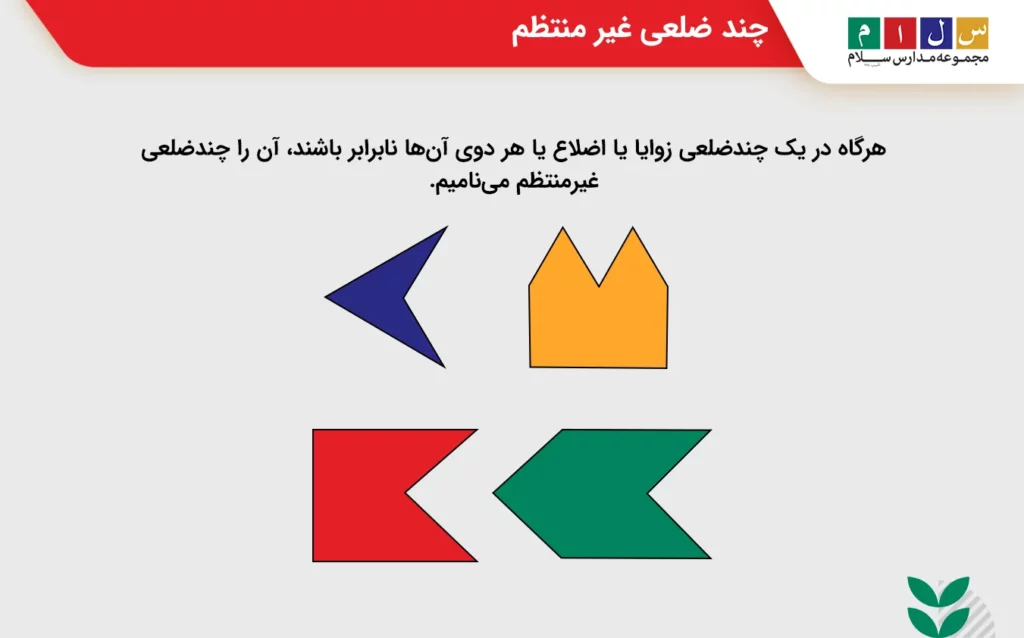
هرگاه در یک چندضلعی زوایا یا اضلاع یا هر دوی آن‌‌ها نابرابر باشند، آن را چندضلعی غیرمنتظم می‌‌نامیم. در تصویر زیر، چند نمونه چندضلعی غیرمنتظم نشان داده شده است.

سخن پایانی

این آموزش را به درس چند ضلعی منتظم چیست هفتم متوسطه اختصاص دادیم و گفتیم چندضلعی‌‌های منتظم را به این دلیل منتظم می‌‌نامیم که اضلاع و زوایای برابرشان نظم خاصی به آن‌‌ها بخشیده است. نکته جالب توجه درمورد این دسته از چندضلعی‌‌ها این است که تعداد اضلاعشان تعیین‌‌کننده تعداد قطرها، اندازه زاویه‌‌ها، تعداد محور تقارن و ویژگی‌‌های دیگر است. بنابراین، با دانستن تعداد اضلاع چندضلعی‌‌های منتظم می‌‌توانید بسیاری از خصوصیات آن‌‌ها را مشخص کنید.

سؤالات متداول

1. چند ضلعی منتظم یعنی چه ؟
   چند ضلعی منتظم نوعی چندضلعی است که زاویه‌‌های آن با هم و اضلاع آن نیز با هم برابرند.
2. نام دیگر چند ضلعی منتظم چیست ؟
   منتظم به معنای مرتب و منظم است و معمولاً این نوع چندضلعی‌‌ها را به همین نام می‌‌خوانند.
3. آیا لوزی چند ضلعی منتظم است ؟
   خیر. لوزی با وجود اضلاع برابر زاویه‌‌های نامساوی دارد.
4. آیا مستطیل چند ضلعی منتظم است ؟
   خیر. زوایای داخلی یک مستطیل با هم برابرند، اما طول اضلاع آن یکسان نیست.
5. آیا مربع چند ضلعی منتظم است ؟
   بله. مربع یک چهارضلعی منتظم است.
6. آیا چند ضلعی منتظم محور تقارن دارد؟
   بله. تمام چندضلعی‌‌های منتظم محور تقارن دارند.