در مقاله محیط چیست توضیح داده‌ایم که اندازه دور تا دور یک شکل هندسی، برابر با اندازه محیط آن است. در این مقاله می‌خواهیم با مثال‌های فراوان، وارد جزئیات تعریفی، محاسباتی و فرمولی محیط مثلث شویم. مثلث یک ۳ ضلعی‌ست که باتوجه به اندازه ضلع‌ها و زوایایش به انواع مختلفی تقسیم می‌شود. بر اساس این تنوع، فرمول‌ها و روش‌های مختلفی هم برای محاسبه محیط مثلث وجود دارد. ما در این مقاله ابتدا فرمول اصلی محیط مثلث را توضیح می‌دهیم و بعد از آن به‌سراغ فرمولهای اختصاصی محیط انواع مثلث متساوی‌الاضلاع، متساوی‌الساقین، قائم‌الزاویه و مختلف‌الاضلاع می‌رویم.
پیشنهاد مطالعه: جدول فرمولهای محیط و مساحت اشکال هندسی
تعریف محیط مثلث
محیط مثلث برابر با اندازه دور تا دور این شکل هندسی است. مثلثها ۳ ضلع دارند که اگر از ابتدای ضلع اول آن شروع به اندازهگیری کنیم و تا انتهای ضلع سوم آن پیش برویم، به اندازه محیط مثلث می‌رسیم.
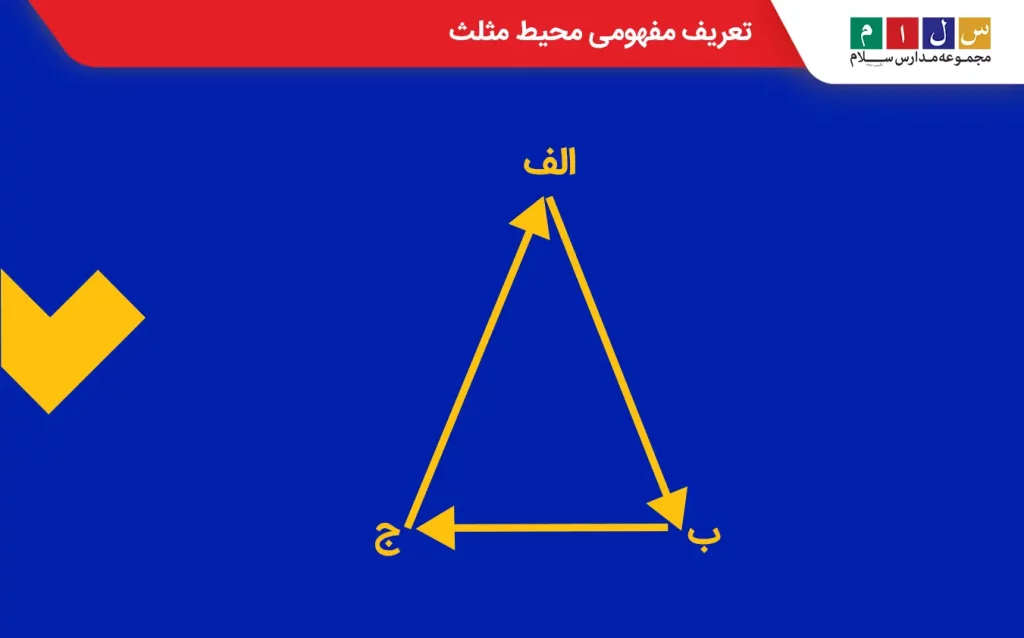
همان‌طور که در تصویر بالا مشاهده می‌کنید، اگر از راس «الف» شروع به اندازهگیری کنیم و بعد از گذر از راس‌های «ب» و «ج»، دوباره به نقطه اول «بازگردیم»، اندازه بهدستآمده برابر با اندازه محیط مثلث است.
مثالی از دنیای واقعی برای محیط مثلث
فرض کنید یک باغچه مثلثی‌شکل کوچک در وسط حیاط خانه‌تان دارید که می‌خواهید دور تا دور آن را فنس یا نرده بکشید. برای این‌کار شما باید ابتدا اندازه ۳ گوشه باغچه را به دست بیاورید و سپس آنها را با هم جمع بزنید. جمع این ۳ گوشه مساوی با محیط باغچه است و به شما نشان می‌دهد که چه مقدار نرده برای حصارکشی دور باغچه نیاز دارید.
اولین نفری باشید که از اخبار و اطلاعیه‌های مرتبط با پایه تحصیلیتان باخبر می‌شود!
فرمول محیط مثلث
فرمول محیط مثلث خیلی ساده است؛ کافی‌ست اندازه ۳ ضلع آن را با هم جمع بزنیم تا به اندازه محیطش برسیم.
اندازه ضلع سوم + اندازه ضلع دوم + اندازه ضلع اول = فرمول محیط مثلث
یا
جمع اندازه ۳ ضلع مثلث = فرمول محیط مثلث
اگر برای هر کدام از ضلعهای یک مثلث نماد داشته باشیم، فرمول محیط مثلث را راحت‌تر می‌نویسیم. اگر نام‌گذاری را با حروف فارسی «الف»، «ب» و «ج» انجام دهیم:
ج + ب + الف = فرمول محیط مثلث
اگر نام‌گذاری ضلع‌ها را با حروف انگلیسی «a» و «b» و «c» انجام دهیم:
c + b + a = P
- a، b و c: اندازه ۳ ضلع مثلث
- P: محیط مثلث
مثال: اندازه ۳ ضلع یک مثلث به‌ترتیب ۴، ۳ و ۵ سانتیمتر است، محیط آن را حساب کنید. جواب: برای محاسبه محیط مثلث فقط کافی‌ست اندازه ۳ ضلع آن را با هم جمع کنیم:
۱۲ = ۵ + ۴ + ۳ = محیط مثلث
حالا بیایید نحوه کارکرد این فرمول را در مثلث‌های مختلف بررسی کنیم:
فرمول محیط مثلث متساوی الاضلاع
در مثلث متساوی‌الاضلاع تمام اضلاع با یکدیگر برابرند. بنابراین، داشتن اندازه یک ضلع مثلث متساوی‌الاضلاع به‌مثابه داشتن اندازه ۳ ضلع آن است. باتوجه به مساوی‌بودن اندازه ۳ ضلع مثلث متساوی‌الاضلاع، می‌توانیم هر ۳ ضلع آن را با یک نماد، مانند «الف» یا «a» نام‌گذاری و فرمول محیط مثلث متساوی الاضلاع را این‌گونه بازنویسی کنیم:
الف × ۳ = الف + الف + الف = محیط مثلث متساوی‌الاضلاع
یا
a+a+a=۳ ×a = محیط مثلث متساوی‌الاضلاع
مثال: اگر اندازه یک ضلع مثلث متساوی‌الاضلاعی برابر با ۴ سانتیمتر باشد، محیط آن چقدر می‌شود؟
جواب: چون اندازه ۳ ضلع مثلث متساوی‌الاضلاع با یکدیگر برابرند، پس اندازه ۳ ضلع مثلث ۴ سانتیمتر است و می‌توانیم به‌جای جمع ۳ ضلع با یکدیگر، اندازه یک‌ضلع (۴) را ضربدر تعداد اضلاع (۳) کنیم:
اندازه یک ضلع × ۳ = فرمول محیط مثلث متساوی‌الاضلاع
۱۲ = ۴ × ۳ = محاسبه محیط مثلث متساوی‌الاضلاع
محیط مثلث متساوی الساقین
وقتی ۲ ضلع مثلثی با یکدیگر برابر باشند، نام آن مثلث، متساوی‌الساقین است. در اینجا هم می‌شود ۲ ضلع مساوی مثلث متساوی‌الساقین را با یک نماد مانند «الف» یا «a» نام‌گذاری کرد و فرمول محیط مثلث متساوی الساقین را به شکل زیر نوشت:
ب + الف × ۲ = ب + الف + الف = محیط مثلث متساوی‌الساقین
یا
a+a+b=۲×a+b = محیط مثلث متساوی‌الساقین
- الف (a): ۲ ضلع مساوی
- ب (b): ضلع نامساوی (ضلع سوم)
مثال: اندازه ۲ ضلعِ هم‌اندازه یک مثلث متساوی‌الساقین ۴ سانتیمتر و اندازه ضلع دیگر آن ۵ سانتیمتر است. باتوجه به این اطلاعات، محیط آن را حساب کنید.جواب: باتوجه به اینکه با یک مثلث متساوی‌الساقین طرف‌ایم، به‌جای جمع ۳ ضلع آن می‌توانیم از فرمول اختصاصی محیط مثلث متساوی‌الساقین برای محاسبه محیط آن استفاده کنیم:
جواب: باتوجه به اینکه با یک مثلث متساوی‌الساقین طرف‌ایم، به‌جای جمع ۳ ضلع آن می‌توانیم از فرمول اختصاصی محیط مثلث متساوی‌الساقین برای محاسبه محیط آن استفاده کنیم:
۲×a+b = محیط مثلث متساوی‌الساقین
۵ + ۴ × ۲ = محیط مثلث متساوی‌الساقین
۱۳ = ۵ + ۸ = محیط مثلث متساوی‌الساقین
محیط مثلث مختلف الاضلاع
به مثلثی که ۳ ضلع نامساوی داشته باشد، مثلث مختلف‌الاضلاع می‌گویند. بهترین روش محاسبه محیط مثلث مختلف‌الاضلاع، جمع ۳ ضلع آن با یکدیگر است:
ج + ب + الف = محیط مثلث مختلف‌الاضلاع
یا
a + b + c = محیط مثلث مختلف‌الاضلاع
مثال: اگر اندازه ۳ ضلع یک مثلث به‌ترتیب ۲، ۴ و ۶ سانتیمتر باشد، اندازه محیط آن چقدر می‌شود؟جواب: باتوجه به اینکه اندازه ۳ ضلع مثلث متفاوت است، پس باید از فرمول محیط مثلث مختلف‌الاضلاع استفاده کنیم. برای محاسبه محیط مثلث مختلف‌الاضلاع به این شیوه عمل میکنیم:
ج + ب + الف = فرمول محیط مثلث مختلف‌الاضلاع
۶ + ۴ + ۲ = فرمول محیط مثلث مختلف‌الاضلاع
۱۲ = فرمول محیط مثلث مختلف‌الاضلاع
فرمول محیط مثلث قائم‌الزاویه
مثلثی را که یکی از زوایایش ۹۰درجه باشد، مثلث قائم‌الزاویه می‌نامند. برای محاسبه محیط مثلث قائم الزاویه هم می‌توان از فرمول اصلی محیط مثلث استفاده کرد و هم می‌توان از قاعده فیثاغورس کمک گرفت. طبق قاعده فیثاغورس:
c² = a² +b²
پس خواهیم داشت:
(c =√ (a²+b²
a: اندازه ضلع عمود بر زاویه قائمه
b: اندازه ضلع میانی یا ستون
c: اندازه وتر
خوبی قاعده بالا این است که اگر اندازه یکی از ۳ ضلع مثلث قائم‌الزاویه را نداشته باشیم، به‌کمک آن به‌راحتی می‌توانیم اندازه ضلع سوم را حساب کنیم. به‌عنوان‌مثال، اگر اندازه وتر را نداشته باشیم، به‌کمک فرمول زیر می‌توانیم محیط مثلث قائم‌الزاویه را در بیاوریم:
(a+b+√(a²+b²۲ = محیط مثلث قائم‌الزاویه
مثال: اندازه ضلع عمود و ضلع ستون یک مثلث قائم‌الزاویه به‌ترتیب ۴ و ۵ سانتیمتر است، اندازه محیط این مثلث چقدر می‌شود؟جواب: چون اندازه ضلع وتر را نداریم، ابتدا از طریق قاعده فیثاغورس آن را محاسبه و سپس آن را در فرمول اصلی محیط مثلث جای‌گذاری میکنیم:
(c = √ (a² + b²
(c = √ (۴² + ۵²
(c = √ (۱۶² + ۲۵²
c=√41=6/40
حالا که اندازه وتر (c) را به دست آوردیم، آن را در فرمول اصلی محیط مثلث می‌گذاریم:
۱۳/۴۰ = ۶/۴۰ + ۴ + ۳ = محاسبه محیط مثلث قائم‌الزاویه
جدول فرمول محیط انواع مثلث
| فرمول عمومی محیط مثلث | c + b + a = P | تصویر مثلث |
| فرمول محیط مثلث متساوی‌الاضلاع | a × ۳P = | تصویر مثلث متساوی‌الاضلاع |
| فرمول محیط مثلث متساوی‌الساقین | b + a × ۲ = P | تصویر مثلث متساوی‌الساقین |
| فرمول محیط مثلث قائم‌الزاویه | a+b+a۲+b۲ = p | تصویر مثلث قائم‌الزاویه |
| فرمول محیط مثلث مختلف‌الاضلاع | c + b + a = P | تصویر مثلث مختلف‌الاضلاع |
مراحل محاسبه محیط مثلث
همان‌طور که دیدید، محاسبه محیط مثلث بسیار ساده است، اما اگر بخواهیم مراحل انجام آن را روی کاغذ بیاوریم، به ۳ مرحله زیر تقسیم می‌شود:
- اندازه هر کدام از اضلاع مثلث را حساب میکنیم.
- مقادیر بهدستآمده را با یکدیگر جمع می‌زنیم.
- جواب را باتوجه به واحد اندازهگیری بیان‌شده در صورت سوال (میلیمتر، متر، سانتیمتر و…) می‌نویسیم.
مثال برای جا افتادن بهتر محیط مثلث در ذهن
حالا که با شیوه محاسبه محیط انواع مثلث آشنا شدید و در خلال بحث، مثال‌هایی را مشاهده کردید، مطمئنا ذهنتان برای حل تمرین آماده است. مثال‌های زیر را برای شروع امتحان کنید:
مثال اول برای محاسبه محیط مثلث
اگر اندازه یکی از ضلعهای مثلث متساوی‌الاضلاعی ۵ سانتیمتر باشد، محیط آن را طبق قاعده ضرب حساب کنید.جواب: این مثال شبیه یکی از مثال‌های محیط مثلث کلاس سوم است. همان‌طور که می‌دانید، ۳ ضلع مثلث متساوی‌الاضلاع با هم برابرند. وقتی ۳ ضلع مساوی داشته باشیم، راحت‌تر از جمع ۳ ضلع، ضرب اندازه یکی از آنها ضربدر تعداد اضلاع (۳) است. بنابراین برای استفاده از قاعده ضرب باید از فرمول زیر استفاده کنیم:
اندازه یک ضلع × ۳ = فرمول محیط مثلث متساوی‌الاضلاع
۱۵ = ۵ × ۳
مثال دوم برای محاسبه محیط مثلث
اگر اندازه محیط مثلثی ۳۵ سانتیمتر باشد و ۲ ضلع آن هر کدام ۱۰ سانتیمتر داشته باشند، اندازه ضلع سوم آن را حساب کنید:
جواب: در صورت سوال اندازه محیط و ۲ ضلع مثلث به ما داده شده و اندازه یکی از ضلعهای آن خواسته شده است. چون ۲ ضلع مثلث با هم برابرند، پس با یک مثلث متساوی‌الساقین طرف‌ایم. بیایید اعداد داده‌شده را در فرمول محیط مثلث متساوی‌الساقین بگذاریم و به اندازه ضلع مجهول برسیم:
a + b × ۲ = محیط مثلث متساوی‌الساقین
+ b ۱۰ × ۲ = ۴۰
+ b ۲۰ = ۴۰
b = ۲۰ – ۴۰
b = ۲۰
مثال سوم برای محاسبه محیط مثلث
اگر اندازه ۳ ضلع یک مثلث برابر با ۳، ۵ و ۷ سانتی‌تر باشد، محیط آن چقدر می‌شود؟جواب: باتوجه به اینکه اندازه ۳ ضلع مثلث متفاوت است، پس با یک مثلث مختلف‌الاضلاع روبه‌روایم. برای به‌دست‌آوردن محیط مثلث مختلف‌الاضلاع باید از فرمول اصلی محیط مثلث استفاده کنیم:
a + b + c = محیط مثلث متساوی‌الاضلاع
۱۵ = ۷ + ۵ + ۳
سخن پایانی
یادتان نرود که فرمول اصلی محیط مثلث (مجموع اندازه ۳ ضلع آن) برای محاسبه محیط تمام مثلثها کاربرد دارد. اما حتما فرمولهای اختصاصی محیط مثلث متساوی‌الاضلاع، متساوی‌الساقین و قائم‌الزاویه را هم یاد بگیرید، زیرا در برخی مواقع در حل مثال‌ها به کارتان می‌آیند. این فرمول‌ها علاوه‌بر کاربردشان در حل محیط مثلث، در یادگیری روابط بین اضلاع انواع مثلث موثرند. روابطی مثل اینکه مثلث‌های متساوی‌الاضلاع دارای ۳ ضلع مساوی‌اند یا در مثلث‌های قائم‌الزاویه، اندازه وتر برابر با جذر ۲ ضلع دیگر به‌توان ۲ است. ما در این مقاله سعی کردیم محیط انواع مثلث را با مثال‌های فراوان و متنوع برایتان محاسبه کنیم. امیدواریم که مطالعه این مقاله برایتان سودمند بوده باشد.
سوالات متداول
- فرمول محیط مثلث چیست؟
فرمول محیط مثلث مساوی با اندازه ۳ ضلع آن است. این فرمول را به زبان ریاضی به این صورت مینویسند: c + b + a = P. در این فرمول، P نماد محیط است و a، b و c نماد ۳ ضلع مثلث هستند. برای انواع مثلثها فرمولهای اختصاصی هم وجود دارد که در متن مقاله به آنها اشاره کردهایم. - محاسبه محیط مثلث چگونه است؟
برای محاسبه محیط مثلث ابتدا باید اندازه هر کدام از ضلعهای آن را به دست آوریم، سپس آنها را با هم جمع بزنیم و در نهایت، مقدار بهدستآمده را باتوجه به واحد اندازهگیری (میلیمتر، سانتیمتر و…) بیان میکنیم. - محیط مثلث چیست؟
منظور از محیط مثلث، اندازه دور تا دور فضای خارجی آن است که از طریق جمع اندازه ۳ ضلع آن به دست میآید. جمع اندازه ۳ ضلع یک مثلث، دقیقا برابر با اندازه دور تا دور سطح بیرونی آن مثلث است.
