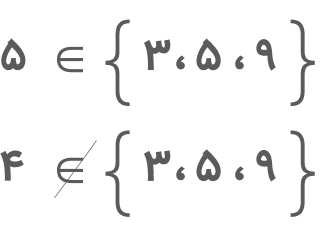مجموعه اعداد چیست؟ ׀ آموزش مجموعه اعداد ریاضی نهم + مثال

اهمیت اعداد در زندگی روزمره انسان بر کسی پوشیده نیست چرا که بدون وجود آن‌‌ها بسیاری از امور روزانه بشر مختل خواهد شد. از گذشته‌‌های دور تا به امروز اعداد مختلفی توسط بشر کشف شده است که هر کدام ویژگی‌‌های خاص خود را دارند. آن دسته از اعدادی که خواص مشترکی دارند، معمولاً در یک گروه قرار داده می‌‌شوند و اصطلاحاً به آن‌‌ها مجموعه اعداد گفته می‌‌شود.

در ریاضی، مجموعه اعداد متعددی وجود دارد که در ادامه این مطلب آن‌‌ها را معرفی خواهیم کرد. علاوه‌‌بر این، تعریفی کلی از مجموعه و قوانین مربوط به آن‌‌ها در ریاضی نیز ارائه خواهیم داد.

تعریف مجموعه در ریاضی نهم

در ریاضی، مجموعه به دسته یا گروهی از اشیاء غیرتکراری یا متمایز گفته می‌‌شود که ویژگی مشترکی دارند. این اشیاء غیرتکراری را که ویژگی مشترکی دارند، عضو مجموعه می‌‌نامیم. طبق این تعریف، یک مجموعه را می‌‌توان مجموعه‌‌ای از افراد، حروف الفبا، اعداد، اشکال، متغیرها و غیره در نظر گرفت.

حتی می‌‌شود برای هر کدام از این مجموعه‌‌ها ویژگی خاصی تعریف کرد و آن‌‌ها را در مجموعه‌‌های جداگانه قرار دارد. برای مثال، می‌‌توان حروف الفبای نقطه‌‌دار و بدون نقطه را به‌‌صورت دو مجموعه مجزا معرفی کرد.

اعضای یک مجموعه درون «آکولاد» که به‌‌صورت {} نمایش داده می‌‌شود قرار می‌‌گیرند و با ویرگول از هم جدا می‌‌شوند. به‌‌عنوان مثال، مجموعه اعداد فرد یک‌‌رقمی به‌‌صورت زیر نمایش داده می‌‌شوند:

{۱,۳,۵,۷,۹}

اعداد بالا یک مجموعه را تشکیل می‌‌دهند زیرا در ویژگی فرد و تک‌‌رقمی بودن اشتراک دارند و هر کدام از آن‌‌ها با دیگری متمایز است. بنابراین، هر یک از اعداد ۱، ۳، ۵، ۷ و ۹ که با علامت ویرگول از هم جدا شده‌‌اند، عضوی از این مجموعه محسوب می‌‌شوند.

نکته ۱: اگر در یک مجموعه عضو تکراری وجود داشته باشد، فقط یک‌‌بار آن را می‌‌نویسیم. مثلاً مجموعه {۱,۱,۳,۱۰,۱۰} را باید به‌‌صورت {۱,۳,۱۰}بنویسیم.

نکته ۲: تغییر در ترتیب قرار گرفتن اعضای یک مجموعه، آن مجموعه را تغییر نمی‌‌دهد. برای مثال، دو مجموعه {۸,۶,۱۱} و {۶,۱۱,۸} هیچ تفاوتی با یکدیگر ندارند.

اگر عضوی متعلق به یک مجموعه باشد، از نماد ∋ و اگر متعلق به مجموعه نباشد، از نماد  ∉   استفاده می‌‌کنیم. برای مثال، می‌‌دانیم که عدد ۵ عضو مجموعه { ۳,۵,۹ } است اما عددی مثل ۴ خیر. بنابراین، اگر بخواهیم تعلق داشتن یا نداشتن این دو عدد را نشان دهیم، نمایش زیر را به‌‌کار می‌‌بریم:

دو عبارت بالا را اینگونه بیان می‌‌کنیم:

• ۵ متعلق است به {۳,۵,۹}
• ۴ متعلق نیست به {۳,۵,۹}

ازآنجا که در ریاضی اغلب با اعداد سروکار داریم، استفاده از مجموعه اعداد رایج‌‌تر است و ازاین‌‌رو شناخت آن‌‌ها برای ما لازم خواهد بود. به همین خاطر، در ادامه این آموزش به معرفی انواع مجموعه ها در ریاضی نهم خواهیم پرداخت.

نام گذاری مجموعه ها

برای استفاده راحت از مجموعه‌‌ها بهتر است آن‌‌ها را نام‌‌گذاری کنیم. معمولاْ این کار را با استفاده از حروف انگلیسی بزرگ مانند A، B، C و مانند آن به‌‌صورت زیر انجام می‌‌دهیم:

A= {۲,۴,۶,۸}
B= { انار,سیب,نارنگی}

مجموعه A اعداد زوج یک‌‌رقمی و مجموعه B میوه‌‌های پاییزی را نشان می‌‌دهد.

زیر مجموعه چیست؟

زیرمجموعه بخشی از یک مجموعه است. برای مثال، دو مجموعه زیر را در نظر بگیرید:

{A= {۰,۳,۴,۹

{B= {۳,۹

همان‌‌طور که می‌‌بینید، تمام اعضای مجموعه B در مجموعه A نیز وجود دارند. در اینجا می‌‌توانیم بگوییم B زیرمجموعه A است. در ریاضی، زیرمجموعه را با علامت نشان می‌‌دهیم و وقتی می‌‌خواهیم بیان کنیم که B زیرمجموعه A است، عبارت زیر را می‌‌نویسیم:

برای نشان دادن مفهوم زیرمجموعه در این مثال، می‌‌توانیم از رسم شکل استفاده کنیم. به‌‌کار بردن شکل، درک این مفهوم ریاضی را آسان‌‌تر خواهد کرد.

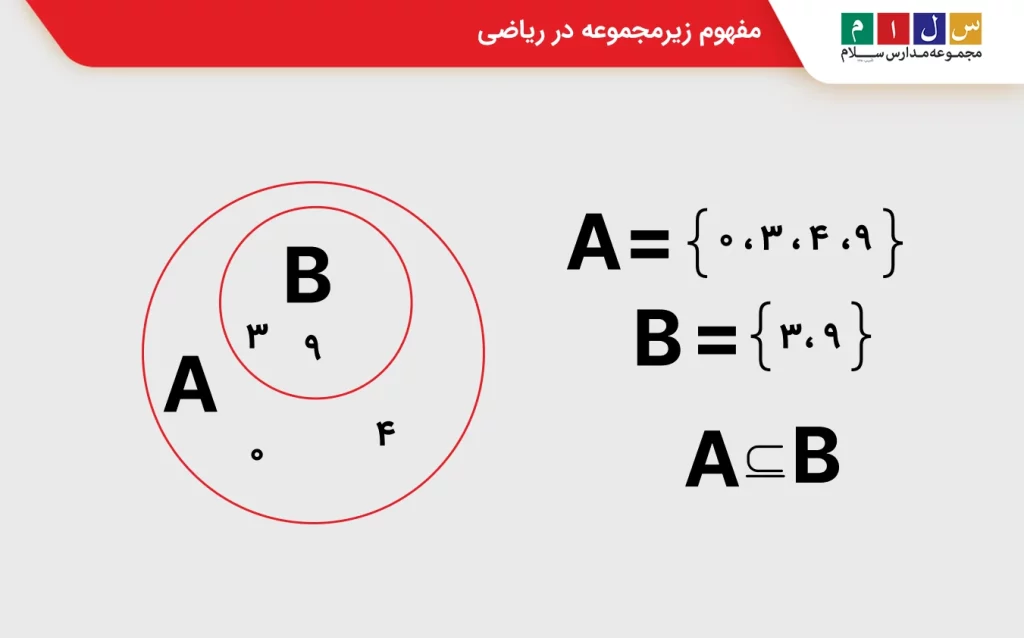
دقت داشته باشید که در مثال ذکرشده، نمی‌‌توانیم بگوییم A⊆B است، زیرا در مجموعه A اعدادی هست که در B وجود ندارد.

نکته مهم: هر مجموعه‌‌ای زیرمجموعه خودش است.

A⊆A

زیرمجموعه محض

زیرمجموعه‌‌های غیر از خود مجموعه را زیرمجموعه محض می‌‌گویند. براساس این تعریف، مجموعه‌‌ای مثل ۳,۸ زیرمجموعه محض ۰,۳,۸,۹ است زیرا ۰ و ۹ در مجموعه اول وجود ندارد. به‌‌طور کلی، اگر B⊆A و A≠B باشد، آنگاه B زیرمجموعه محض A خواهد بود.

نکته: تعداد زیرمجموعه‌‌های مجموعه‌‌ای با n عضو برابر است با ۲ⁿ. برای مثال، اگر مجموعه‌‌ای با ۴ عضو داشته باشیم، تعداد زیرمجموعه‌‌های آن مساوی است با

۲^۴=۱۶

پیشنهاد مطالعه: اعداد مرکب چیست؟

مجموعه متناهی چیست؟

مجموعه متناهی مجموعه‌‌ای است که تعداد اعضای آن محدود و قابل شمارش است. البته این را در نظر داشته باشید هر مجموعه‌‌ای که بتوان اعضای آن را شمارش کرد لزوماً مجموعه متناهی نیست. مجموعه زیر که ۶ عضو دارد نمونه‌‌ای از یک مجموعه متناهی است.

{A = {۳,۶,۹,۱۲,۱۵,۱۸

مجموعه نامتناهی به مجموعه‌‌ای گفته می‌‌شود که تعداد اعضای آن مشخص نیست؛ به‌‌عبارتی تعداد اعضای آن بی‌‌نهایت است. نوشتن تمام اعضای یک مجموعه نامتناهی کاری غیرممکن است، به همین دلیل تنها چند عضو نخست آن را می‌‌نویسیم و به‌‌جای باقی اعضای آن از سه نقطه (…) استفاده می‌‌کنیم.

{B= {۱,۲,۳,۴

مجموعه های برابر

اگر دو یا چند مجموعه داشته باشیم که اعضای یکسانی دارند و تعداد اعضای آن‌‌ها نیز برابر است، آنگاه این مجموعه‌‌ها را مجموعه‌‌های برابر می‌‌گوییم.
{A = {۱,۲,۳ و {B ={۳,۱,۲ دو مجموعه برابر هستند زیرا هر دوی آن‌‌ها ۳ عضو یکسان دارند. مجموعه‌‌های مساوی را با علامت = نشان می‌‌دهیم. با توجه به اینکه دو مجموعه A و B با هم برابرند، می‌‌نویسیم A=B. همان‌‌طور که قبلاً هم اشاره کردیم، در مجموعه‌‌های برابر ترتیب قرار گرفتن اعضا تأثیری در برابر بودن یا نبودن مجموعه‌‌ها ندارد.

نکته مهم: اگر دو مجموعه A و B داشته باشیم که هر دو زیرمجموعه یکدیگرند یعنی A⊆B و B⊆A، آنگاه A=B خواهد بود.

مجموعه جهانی چیست؟

مجموعه جهانی که به آن مجموعه مرجع هم می‌‌گویند، مجموعه‌‌ای شامل تمام مجموعه‌‌های مربوط به یک موضوع خاص است که می‌‌خواهیم روی آن‌‌ها عملیات انجام دهیم. مجموعه جهانی را با حرف یو بزرگ (U) نمایش می‌‌دهند. به‌‌عنوان مثال، برای مطالعه تمام وسایل نقلیه، مجموعه مرجع را وسایل نقلیه در نظر می‌‌گیریم که در این صورت، مجموعه اتومبیل‌‌ها، دوچرخه‌‌ها و قطارها زیرمجموعه این مجموعه جهانی هستند.

مجموعه مرجع را باید به‌‌گونه‌‌ای انتخاب کنیم که تمام اعضای زیرمجموعه‌‌ها در آن قرار گیرند. با یک مثال، این موضوع را بررسی می‌‌کنیم. فرض کنید دو مجموعه A و B را داریم:

{A= {۰,۳,۱۱,۱۴,۲۰

{B= {۳,۹,۱۴,۱۶,۱۷

مجموعه جهانی را باید به‌‌گونه‌‌ای تعریف کنیم که اعضای تکراری در آن وجود نداشته باشد:

{U= {.,۳,۹,۱۱,۱۴,۱۶,۱۷,۲۰

با توجه به مجموعه مرجع می‌‌توان گفت A ‌و B زیرمجموعه U هستند:

A⊆U
B⊆U

مجموعه تهی چیست؟

مجموعه‌‌ای که هیچ عضوی ندارد مجموعه تهی نامیده می‌‌شود. این مجموعه را با نماد ∅ (فی) یا {} نمایش می‌‌دهند. مجموعه تهی زیرمجموعه تمام مجموعه‌‌هاست. دقت داشته باشید منظور از مجموعه تهی، مجموعه صفر نیست. مجموعه صفر یعنی مجموعه‌‌ای که عدد صفر تنها عضو آن است و آن را به‌‌صورت {۰} نشان می‌‌دهند، درحالی که مجموعه تهی هیچ عضوی ندارد.

نکته مهم: مجموعه {∅} مجموعه تهی محسوب نمی‌‌شود.

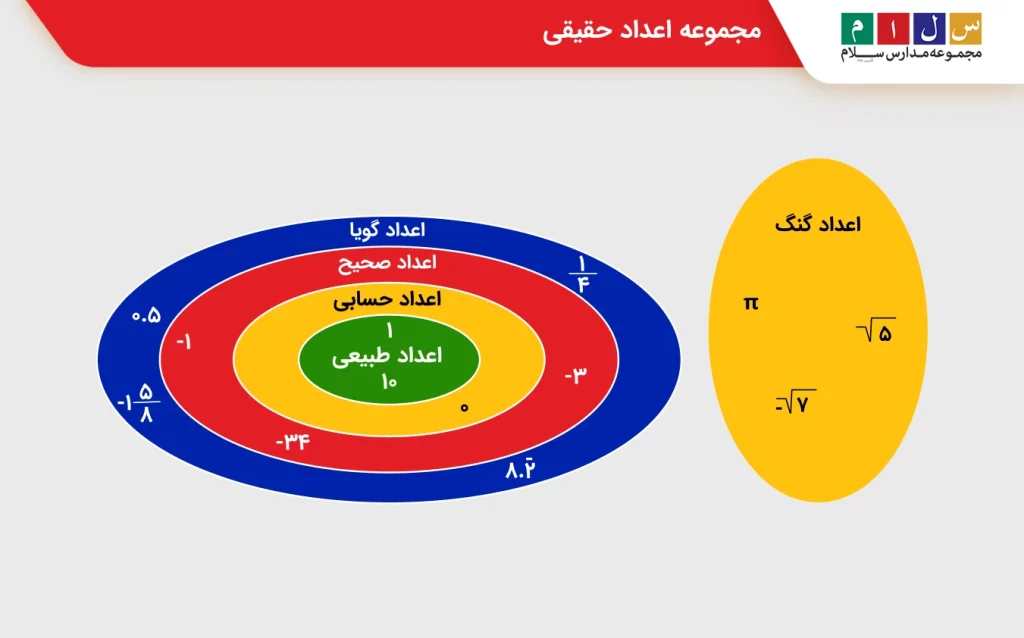
مجموعه اعداد طبیعی

مجموعه اعداد طبیعی مجموعه‌‌ای نامتناهی است که از ۱ شروع می‌‌شود و تا بی‌‌نهایت ادامه دارد. مجموعه اعداد طبیعی را با حرف N نمایش می‌‌دهند.

{… ,N= {۱,۲,۳,۴,۵

مجموعه اعداد حسابی

مجموعه اعداد حسابی نیز مجموعه‌‌ای نامتناهی شامل عدد صفر و تمام اعداد صحیح مثبت است. مجموعه اعداد حسابی را با نماد W نشان می‌‌دهیم.

{…,W= {۰,۱,۲,۳,۴,۵

مجموعه اعداد طبیعی زیرمجموعه اعداد حسابی است.

مجموعه اعداد صحیح

اعداد صحیح اعدادی کامل و قابل شمارش هستند که اعداد مثبت و منفی و عدد صفر را شامل می‌‌شوند. مجموعه اعداد صحیح به‌‌صورت زیر نمایش داده می‌‌شود:

{ …,Z = {…,-۲,-۱,۰,۱,۲

مجموعه اعداد طبیعی و حسابی زیرمجموعه اعداد صحیح هستند.

مجموعه اعداد گویا

اعداد گویا اعدادی کسری هستند که صورت و مخرجشان یک عدد صحیح است (مخرج نمی‌‌تواند صفر باشد). اعداد زیر در مجموعه اعداد گویا قرار می‌‌گیرند:

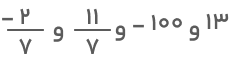
مجموعه اعداد طبیعی، حسابی و صحیح زیرمجموعه اعداد گویا محسوب می‌‌شوند. مجموعه اعداد گویا را با حرف Q نشان می‌‌دهیم.

مجموعه اعداد گنگ

مجموعه اعداد گنگ (Q’) مجموعه‌‌ای از اعداد حقیقی هستند که نمی‌‌توان آن‌‌ها را به‌‌صورت عدد گویا یا کسر ساده بیان کرد. اگر این گروه از اعداد را به‌‌صورت عدد اعشاری نشان دهیم، رقم‌‌های اعشار آن بی‌‌نهایت و تکرارناپذیر خواهد بود. عدد پی و اعداد رادیکالی مانند ۲√ در دسته اعداد گنگ قرار می‌‌گیرند.

مجموعه اعداد حقیقی

تمام مجموعه اعدادی که تا اینجا معرفی کردیم، مجموعه اعداد حقیقی را تشکیل می‌‌دهند یا به‌‌عبارتی زیرمجموعه اعداد حقیقی هستند. این مجموعه اعداد با نماد R نشان داده می‌‌شود. با توجه به این توضیحات می‌‌توان مجموعه اعداد حقیقی را مجموعه جهانی یا مرجع برای مجموعه اعداد نام‌‌برده دانست. شکل زیر این موضوع را به‌‌خوبی نشان می‌‌دهد.

برای آشنایی بیشتر با مجموعه اعداد و تفاوت آن‌‌ها با یکدیگر می‌‌توانید فایل pdf مجموعه ها در ریاضی را دانلود کنید تا برای همیشه آن را دردسترس داشته باشید.

مجموعه یکانی چیست؟

مجموعه یکانی مجموعه‌‌ای است که تنها یک عضو دارد. مانند اعداد زوج بین ۱۱ و ۱۳ که فقط یک عضو دارد و به‌‌صورت {۱۲} نوشته می‌‌شود.

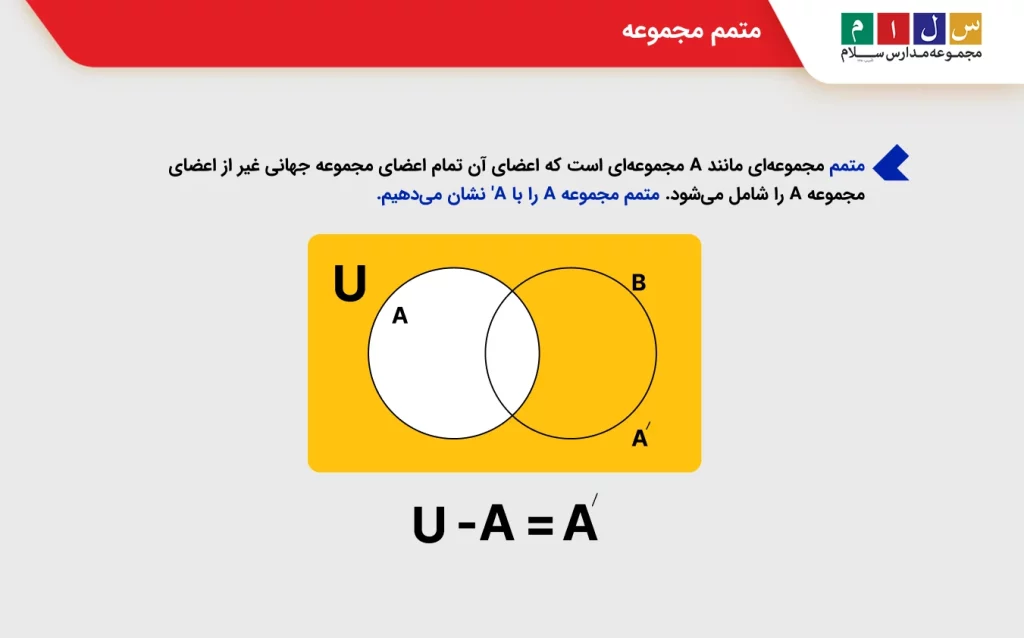
متمم مجموعه چیست؟

متمم مجموعه‌‌ای مانند A مجموعه‌‌ای است که اعضای آن تمام اعضای مجموعه جهانی غیر از اعضای مجموعه A را شامل می‌‌شود. متمم مجموعه A را با A′ نشان می‌‌دهیم.

U – A = A’

مثال: مجموعه مرجع زیر را در نظر بگیرید:

{U= {۰,۳,۹,۱۱,۱۴,۱۶,۱۷,۲۰

اگر مجموعه A به‌‌صورت {,۹,۱۱,۱۶,۱۷,۲۰ ,۰ } باشد، آنگاه متمم مجموعه A به‌‌شکل زیر خواهد بود:

{A’= {۳,۱۴

نکته: متمم یک مجموعه جهانی، مجموعه تهی است.

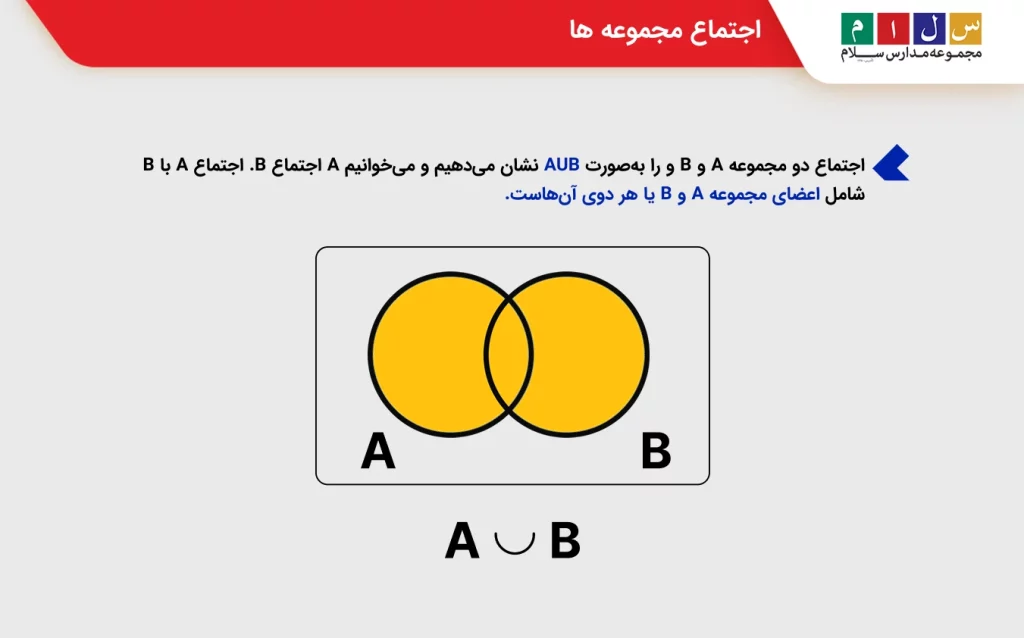
اجتماع مجموعه ها

اجتماع دو مجموعه A و B و را به‌‌صورت AUB نشان می‌‌دهیم و می‌‌خوانیم A اجتماع B. اجتماع A با B شامل اعضای مجموعه A و B یا هر دوی آن‌‌هاست.

برای مثال، اجتماع دو مجموعه { ۱,۳ } با { ۱,۴} مساوی با{ ۱,۳,۴} است.

توجه داشته باشید که علامت اجتماع (U) با نماد مجموعه جهانی متفاوت است.

پیشنهاد مطالعه: اعداد متوالی چیست؟

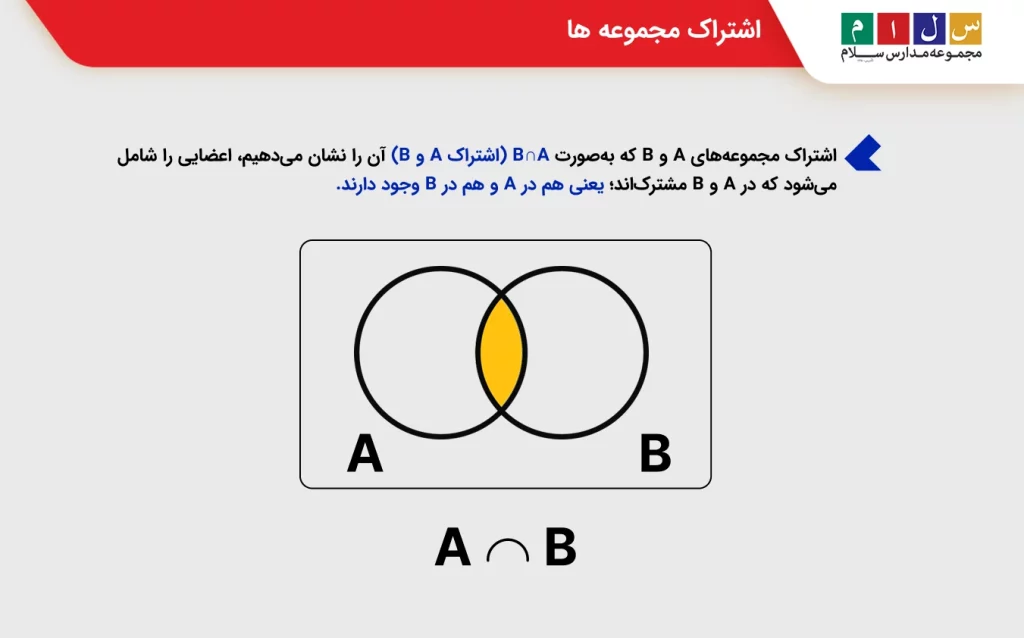
اشتراک مجموعه ها

اشتراک مجموعه‌‌های A و B که به‌‌صورت B∩A (اشتراک A و B) آن را نشان می‌‌دهیم، اعضایی را شامل می‌‌شود که در A و B مشترک‌‌اند؛ یعنی هم در A و هم در B وجود دارند.

مثال زیر نمونه خوبی از اشتراک دو مجموعه است.

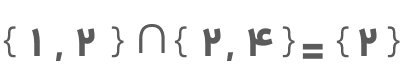
تعداد اعضای B∩A از رابطه زیر قابل محاسبه است:

اگر این فرمول را برای به‌‌دست آوردن تعداد اعضای {۱,۲} ∪ {۲,۴} به‌‌کار ببریم خواهیم داشت:

می‌‌بینیم که اشتراک دو مجموعه بالا تنها یک عضو دارد و آن هم عدد ۲ است.

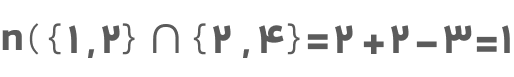
می‌‌بینیم که اشتراک دو مجموعه بالا تنها یک عضو دارد و آن هم عدد ۲ است.

تفاضل مجموعه ها

تفاضل مجموعه B از A به‌‌صورت A-B نوشته می‌‌شود و منظور از آن، تمام اعضایی از مجموعه A است که در مجموعه B وجود ندارند. مثلاً اگر دو مجموعه به‌‌صورت زیر داشته باشیم، تفاضل آن‌‌ها به‌‌شکل زیر خواهد بود:

{A= {۰,۳,۸,۲۰

{B= {۳,۲۰,۱۴,۲۵

{ A – B = {۰,۸

قوانین مجموعه ها در ریاضی

مجموعه‌‌ها مانند اعداد خاصیت شرکت‌‌پذیری، جابه‌‌جایی و غیره دارند. اگر سه مجموعه مانند A، B و C داشته باشیم، آنگاه می‌‌توان ویژگی‌‌های زیر را برای آن‌‌ها برشمرد.

ویژگی‌‌ها	نمایش ویژگی‌‌ها
خاصیت جابه‌‌جایی	A∩B = B∩A A∪B = B∪A
خاصیت شرکت‌‌پذیری	A∪(B ∪ C) = (A ∪ B)∪C A∩(B∩C) = (A∩B)∩C
خاصیت توزیع‌‌پذیری	(A∪(B∩C)=(A∪B)∩(A∪C (A∩(B∪C) =(A∩B)∪(A∩C
خاصیت همانی	A∪∅=A A∩U=A
خاصیت متمم بودن	A∪A’=U
خاصیت خودتوانی	A∪A=A A∩A=A
خاصیت مجموعه تهی و مرجع	A∪∅=A A∩∅=∅ A∪U=U A∩U=A

سخن پایانی

این آموزش از مجموعه آموزش‌‌های ریاضی را به بررسی مجموعه اعداد اختصاص دادیم و مجموعه‌‌های مهم در ریاضی را با ذکر مثال نام بردیم. شناخت مجموعه‌‌ها می‌‌تواند دریچه‌‌ای به‌‌سوی درک بهتر مفاهیم ریاضی باشد و از این نظر بهتر است آن‌‌ها را به‌‌خوبی یاد بگیریم و به ذهنمان بسپاریم.

تردیدی نیست که مانند هر مبحث دیگری در ریاضی، حل مسئله برای فهم عمیق‌‌تر و تسلط بر مطالب راه‌‌گشا خواهد بود. پس حل تمرین در این زمینه را فراموش نکنید.ز مجموعه آموزش‌‌های ریاضی را به بررسی مجموعه اعداد اختصاص دادیم و مجموعه‌‌های مهم در ریاضی را با ذکر مثال نام بردیم.

شناخت مجموعه‌‌ها می‌‌تواند دریچه‌‌ای به‌‌سوی درک بهتر مفاهیم ریاضی باشد و از این نظر بهتر است آن‌‌ها را به‌‌خوبی یاد بگیریم و به ذهنمان بسپاریم. تردیدی نیست که مانند هر مبحث دیگری در ریاضی، حل مسئله برای فهم عمیق‌‌تر و تسلط بر مطالب راه‌‌گشا خواهد بود. پس حل تمرین در این زمینه را فراموش نکنید.