فهرست مطالب
Toggleگاهی اوقات مقدار صورت و مخرج یک کسر بهگونهای است که نمیتوانیم بهخوبی مقدار عددی آن را درک کنیم. درواقع، زمانی که مقدار صورت از مقدار مخرج کسر بزرگتر است، درک مفهوم جزء از کل آن کسر دشوارتر میشود. در چنین شرایطی، بهتر است کسر موردنظر را طوری نشان دهیم که درک مقدار عددی آن برایمان راحتتر شود.
راهحل مناسب برای نمایش چنین کسرهایی که صورت آنها از مخرجشان بزرگتر است، استفاده از عدد مخلوط است. احتمالاً میپرسید عدد مخلوط چیست. با این آموزش همراه باشید تا هم پاسخ این پرسش را دریافت کنید و هم با کمک تمرینهایی که در این مقاله آوردهایم، با دنیای این اعداد بیشتر آشنا شوید.
عدد مخلوط چیست؟
این اعداد از نامشان مشخص است که مخلوط یا ترکیبی از اعداد هستند. درواقع عدد مخلوط، ترکیبی از دو عدد است: یک عدد صحیح یا کامل و یک عدد کسری. اعداد مخلوط معمولاً اعداد مناسبی برای نمایش کسرهای بزرگتر از واحد هستند. منظور از کسر بزرگتر از واحد کسری است که مقدار صورتش از مقدار مخرج بزرگتر باشد. بهبیانی دیگر، در چنین کسری قدر مطلق صورت از قدر مطلق مخرج بزرگتر است.
با توجه به تعریف عدد مخلوط، میتوان گفت که عدد مخلوط، عددی بین دو عدد صحیح یا کامل است. تصویر زیر را نگاه کنید. این تصویر، سه مربع را نشان میدهد که هر کدام به ۸ قسمت مساوی تقسیم شدهاند. از این سه مربع، دو مربع بهطور کامل رنگ شدهاند، اما در مربع سوم تنها ۵ قسمت از ۸ قسمت رنگ شده است. بنابراین، در این شکل دو مربع کامل و پنجهشتم از یک مربع دیده میشود. عدد مخلوط مربوط به این شکل را بهصورت زیر مینویسیم و میخوانیم دو و پنجهشتم:
در این مثال، عدد کامل عدد دو و عدد کسری پنجهشتم است.
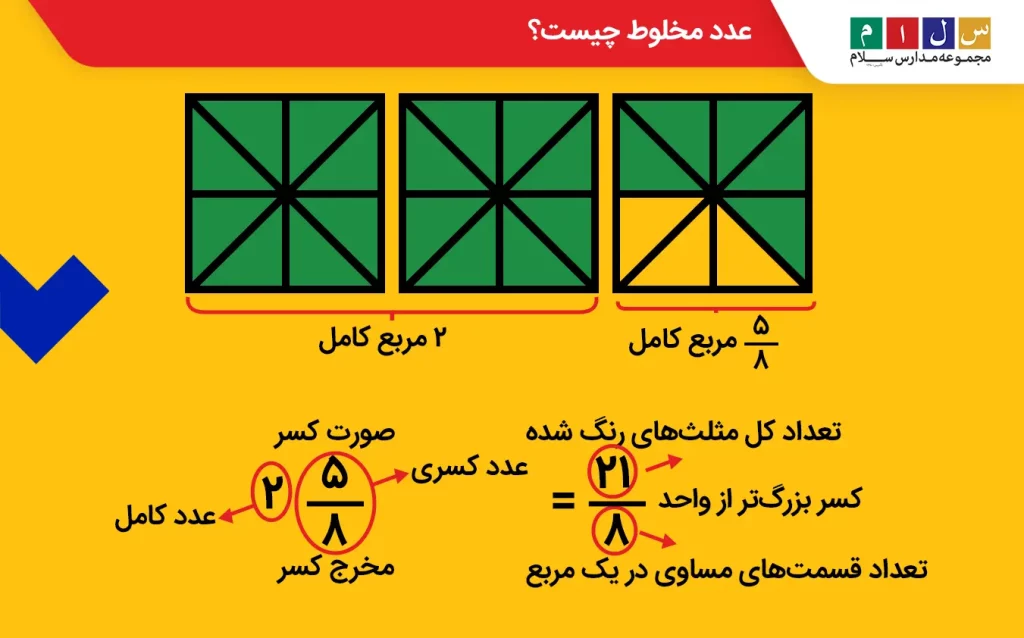
اگر بهجای اینکه قسمت رنگشده در تصویر زیر را با عدد مخلوط نشان دهیم، بهصورت کسری آن را نمایش میدادیم، یک کسر بزرگتر از واحد داشتیم که درک درستی از شکل به ما نمیداد، اما با کمک عدد مخلوط میتوانیم بهراحتی مفهوم کسر موردنظر را درک کنیم.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
نمایش عدد مخلوط روی محور
حالا که با عدد مخلوط و اجزای آن آشنا شدید، سراغ نحوه نمایش این اعداد روی محور میرویم تا ببینیم این اعداد روی محور چگونه نشان داده میشوند. فرض کنید میخواهیم عدد مخلوط زیر (سه و دوپنجم) را روی محور اعداد نشان دهیم.
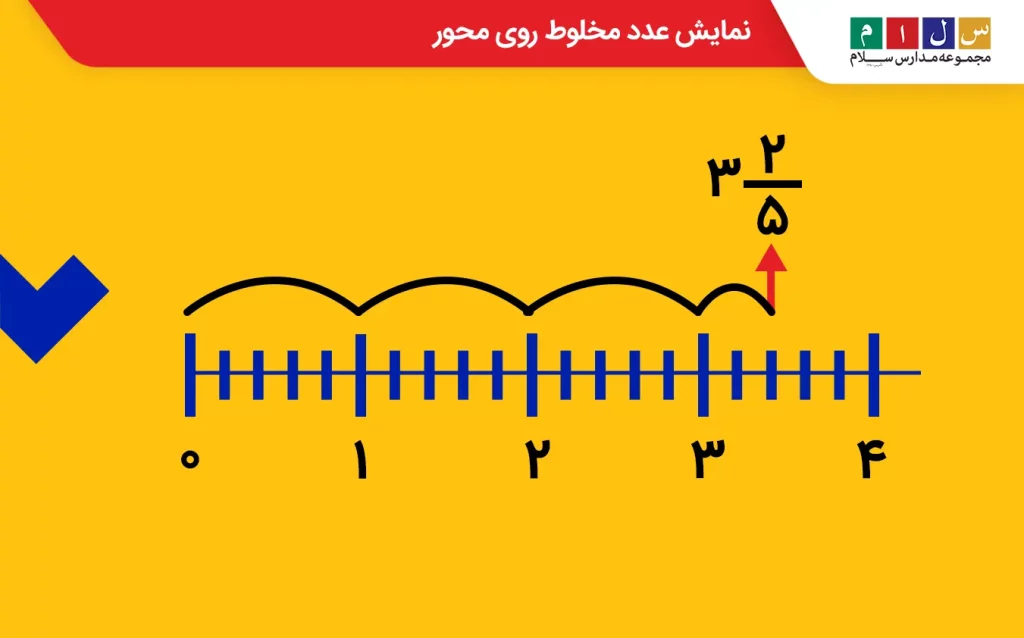
از نحوه خواندن این عدد مشخص است که در اینجا ما سه واحد کامل و دوپنجم از یک واحد کامل را داریم. این یعنی اینکه باید از صفر محور بهاندازه ۳ واحد کامل بشماریم و جلو برویم. اما برای بخش کسری که دوپنجم یک واحد است باید یک واحد کامل را به ۵ قسمت مساوی تقسیم کنیم و ۲ قسمت از ۵ قسمت را جدا کنیم. به شکل زیر نگاه کنید تا بهتر متوجه شوید.
پیشنهاد مطالعه: آموزش کسر روی محور
نمایش عدد مخلوط با شکل
استفاده از شکل، یک روش مفید برای فهم عدد مخلوط است. برای مثال، اگر در نظر داشته باشیم که عدد زیر (پنج و دوسوم) را با کمک یک شکل نشان دهیم:
بهصورت زیر عمل میکنیم:
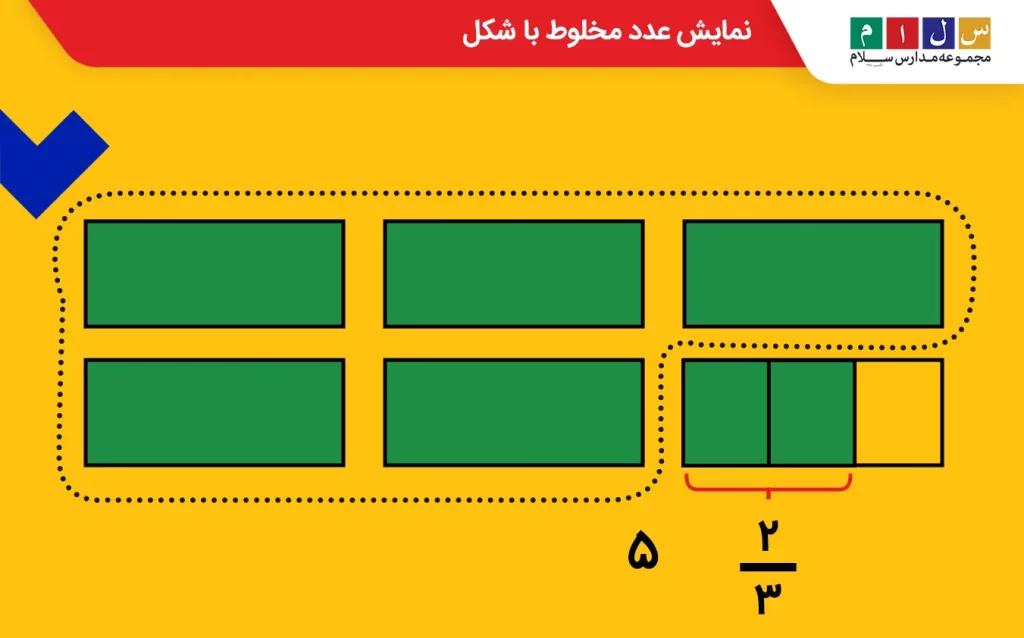
چون در اینجا ۵ واحد کامل داریم، ابتدا ۵ شکل یکسان مانند مستطیل رسم میکنیم. البته از شکلهای دیگری هم میتوانید استفاده کنید، اما باید دقت داشته باشید که شکل بهگونهای باشد که بتوانید آن را به قسمتهای مساوی تقسیم کنید.
حالا برای نشان دادن بخش کسری یعنی دوسوم، یک مستطیل بهاندازه ۵ مستطیل دیگر رسم میکنیم و آن را به ۳ قسمت مساوی تقسیم میکنیم چون میخواهیم دو قسمت از سه قسمت (دوسوم) را نشان دهیم. پس از تقسیم کردن مستطیل به سه قسمت، دو قسمت از آن را رنگآمیزی میکنیم تا بخش کسری عدد مخلوط بهخوبی نشان داده شود.
روشهای تبدیل کسر به عدد مخلوط
کسر ناسره کسری است که مقدار عددی صورت آن از مخرجش بیشتر است، یعنی مقداری بزرگتر از عدد یک دارد. این نوع کسر را میتوان بهصورت یک عدد مخلوط (ترکیبی از عدد صحیح و کسر) نوشت. روشهای مختلفی برای تبدیل کسر به عدد مخلوط وجود دارد که در ادامه به توضیح هرکدام میپردازیم.
پیشنهاد مطالعه : ضرب اعداد مخلوط
روش اول: تقسیم صورت بر مخرج
گامهای تبدیل کسر ناسره به عدد مخلوط با این روش، بهشرح زیر است:
- صورت را بر مخرج کسر تقسیم کنید.
- بعد از تقسیم، یک عدد بهعنوان خارجقسمت خواهید داشت که همان عدد صحیح کسر مخلوط است.
- باقیماندهی تقسیم صورت، صورتِ کسر عدد مخلوط است.
- مخرج کسر همان مخرج عدد اصلی است.
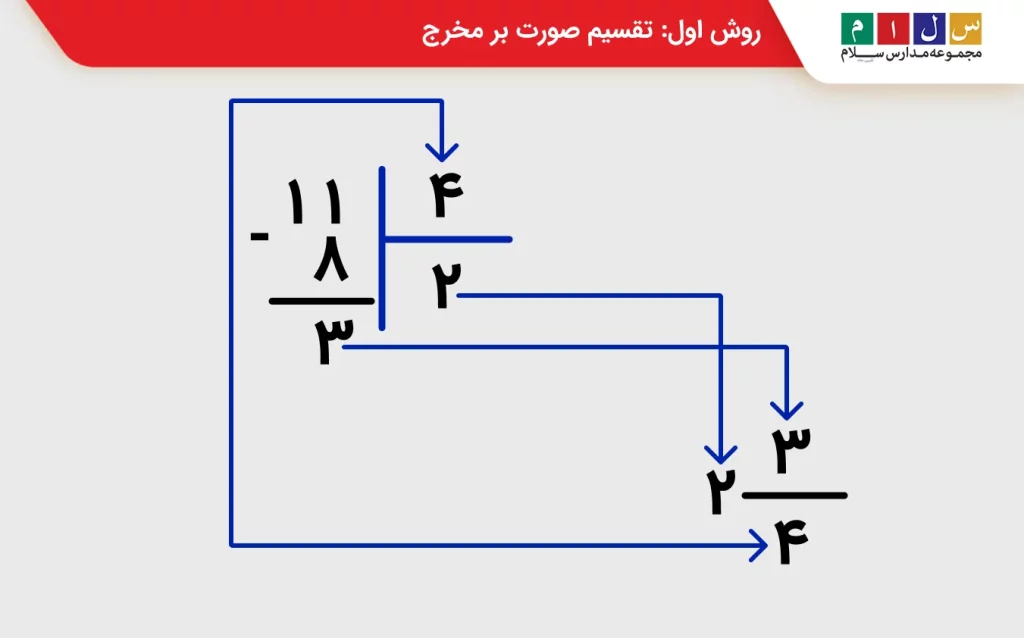
برای مثال، فرض کنید میخواهیم طبق گامهای بالا، کسر 11/4 را به یک عدد مخلوط تبدیل کنیم.
- ابتدا عدد 11 را بر 4 تقسیم میکنیم.
- سپس خارجقسمت برابر 2 و باقیمانده برابر 3 است.
- خارجقسمت (یعنی 2) عدد صحیحِ کسر مخلوط میشود.
- باقیمانده (یعنی 3) صورت کسر و مخرج همان 4 است.
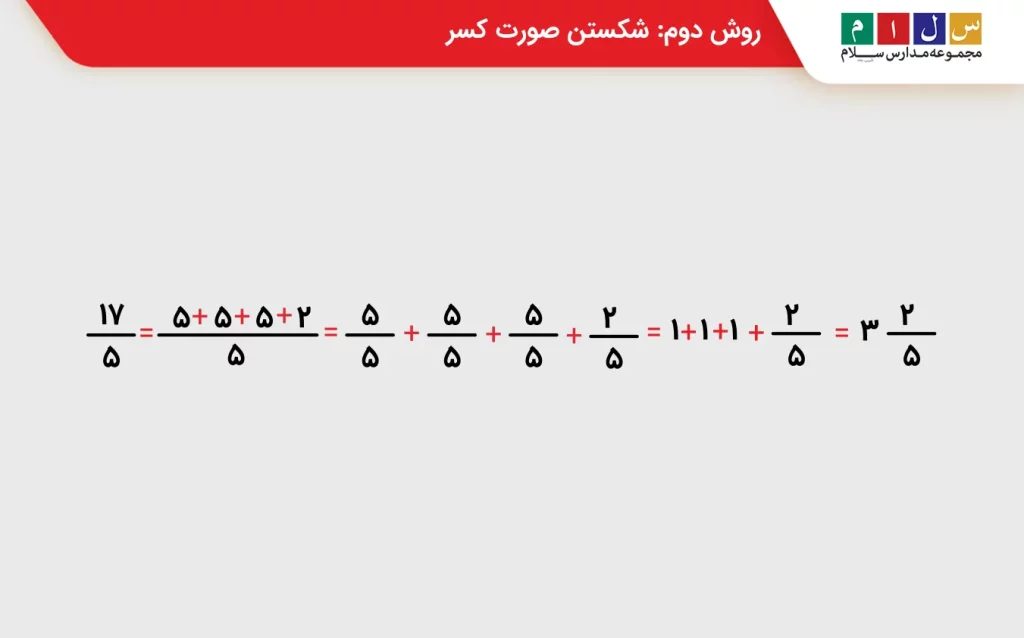
روش دوم: شکستن صورت کسر
در این روش، صورت کسر را به اندازه عدد مخرج میشکنیم.
برای مثال، اگر کسر 17/5 را داشته باشیم، به این صورت عمل میکنیم:
روش سوم: استفاده از مضرب مخرج
در این روش، بزرگترین مضرب مخرج را که کوچکتر از صورت باشد، پیدا میکنیم و آن را با عددی جمع میکنیم که حاصل این جمع برابر با صورت شود.
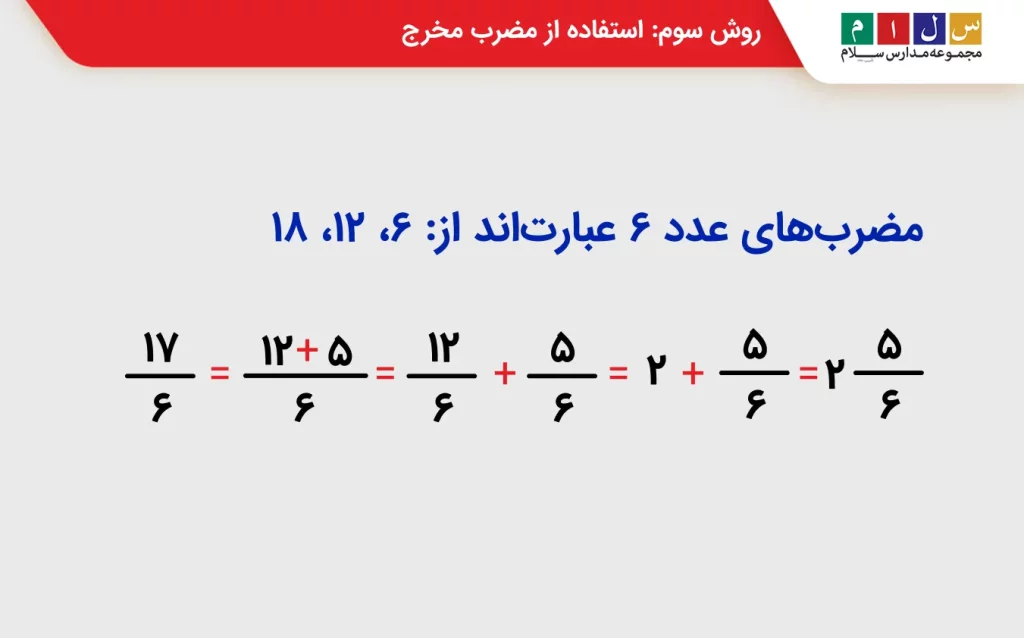
برای مثال اگر بخواهیم کسر 17/6 را به یک عدد مخلوط تبدیل کنیم، باید بزرگترین مضرب عدد 6 را پیدا کنیم که کوچکتر از 17 باشد.
مضربهای عدد 6 عبارتاند از: 6، 12، 18
بزرگترین مضرب کوچکتر از 17، عدد 12 است.
حال مینویسیم:
اگر مایل هستید با تمام این روشها به طور کاملتری آشنا شوید، پیشنهاد ما این است که سری به مقاله تبدیل کسر به عدد مخلوط بزنید.
تبدیل عدد مخلوط به کسر
روش تبدیل کسر به عدد مخلوط را یاد گرفتیم. حال این سؤال پیش میآید که آیا میتوان برعکس این تبدیل را انجام داد؛ یعنی آیا میتوان عدد مخلوط را به کسر تبدیل کرد. پاسخ مثبت است. برای تبدیل عدد مخلوط به کسر، باید مراحل زیر را طی کنیم:
- مرحله اول: ابتدا عدد صحیح را در مخرج ضرب میکنیم.
- مرحله دوم: مقدار بهدستآمده در مرحله اول را با صورت کسر جمع میزنیم.
- مرحله سوم: حاصل جمع مرحله دوم را در صورت کسر جایگذاری میکنیم و مقدار مخرج را همان مقدار مخرج عدد مخلوط قرار میدهیم.
بهعنوان نمونه، در تصویری که در ادامه آمده، مراحل تبدیل عدد زیر به یک کسر را نشان دادهایم.

تبدیل عدد مخلوط به عدد اعشاری
در آموزش اعداد اعشاری آموختیم که این اعداد وقتی به کسر تبدیل میشوند، مخرجشان ضریبی از ۱۰ است مانند ۱۰، ۱۰۰، ۱۰۰۰ و مانند اینها. بنابراین، اگر بخواهیم عدد مخلوط را به عدد اعشاری تبدیل کنیم، باید کاری کنیم که مخرج آن به ضریبی از ۱۰ شود. مثلاً اگر بخواهیم عدد زیر را به عدد اعشاری تبدیل کنیم:
باید طبق مراحل زیر پیش برویم.
عدد مخلوط را میتوان بهشکل زیر نوشت:
حالا باید صورت و مخرج عبارت کسری را در عددی ضرب کنیم که مخرج کسر ضریبی از ۱۰ شود.
درنتیجه خواهیم داشت :
جمع و تفریق اعداد مخلوط
جمع و تفریق اعداد مخلوط مراحلی مشابه هم دارند. تنها تفاوت آنها این است که در جمع، اعداد مخلوط را جمع میزنیم و در تفریق، این اعداد را از هم کم میکنیم. بنابراین، در اینجا فقط عمل جمع اعداد مخلوط را توضیح میدهیم. برای جمع اعداد مخلوط به مخرج کسر آنها نگاه میکنیم. اگر مخرج آنها مانند هم بود، ابتدا اعداد صحیح یا کامل و سپس کسرهای آنها را جداگانه جمع میکنیم. به مثال زیر توجه کنید.
میخواهیم دو عدد مخلوط زیر را با هم جمع کنیم.
همانطور که میبینید، مخرج هر دو عدد مانند هم و برابر با ۱۱ است. بنابراین، دو عدد صحیح را با هم و دو عدد کسری را با یکدیگر بهصورت زیر جمع میزنیم:
۱۳ + ۷ = ۲۰
درنتیجه جواب نهایی ما بهشکل زیر خواهد بود:
اکنون ممکن است این سؤال پیش آید که اگر مخرجها نامساوی باشند، عمل جمع اعداد مخلوط چگونه خواهد بود. با یک مثال، این حالت را توضیح میدهیم. دو عدد زیر را در نظر بگیرید:
مخرج این اعداد با هم برابر نیست. در چنین حالتی، ابتدا اعداد صحیح دو عدد مخلوط را جداگانه با هم جمع میکنیم:
۹ + ۸= ۱۷
پس از آن، نوبت جمع کردن کسرهاست. باید با گرفتن مخرج مشترک کاری کنیم که مخرج این کسرها مساوی شود و سپس آنها را جمع بزنیم. کوچکترین مضرب مشترک ۴ و ۶ برابر با ۱۲ است.
بنابراین، حاصل جمع دو عدد مخلوط برابر است با
نکتهای که در اینجا لازم است به آن اشاره کنیم این است که برای جمع اعداد مخلوط میتوانید بهجای این مراحل، از همان ابتدا آنها را بهروشی که در بخشهای قبل آموختیم، به کسر تبدیل کنید و سپس عمل جمع را انجام دهید.
ضرب و تقسیم اعداد مخلوط
انجام ضرب و تقسیم اعداد مخلوط مانند جمع و تفریق آنها بسیار ساده و راحت است. البته شاید تصور کنید برای ضرب و تقسیم اعداد مخلوط مانند جمع و تفریق آنها باید اعداد صحیح و اعداد کسری را جداگانه در هم ضرب یا بر هم تقسیم کنید، اما این تصور کاملاً اشتباه است. برای ضرب و تقسیم این اعداد تنها کافیست آنها را ابتدا به کسر تبدیل کنید و سپس کسرهای بهدستآمده را در هم ضرب یا بر هم تقسیم کنید.
برای مثال، اگر بخواهیم حاصل ضرب اعداد زیر را بهدست آوریم:
ابتدا باید هر کدام از آنها را با روشی که گفتیم به کسر تبدیل کنیم.
حالا کسرهای بهدستآمده را در هم ضرب میکنیم. صورت در صورت و مخرج در مخرج ضرب میشود.
پیشنهاد مطالعه: آموزش ضرب کسرها به زبان ساده
اگر بخواهیم جواب را بهصورت عدد مخلوط بنویسیم، میتوانیم با کمک گستردهنویسی بهراحتی این کار را انجام دهیم.
بنابراین، پاسخ ضرب دو عدد مخلوط را میتوانیم بهصورت زیر بازنویسی کنیم:
برای تقسیم اعداد مخلوط، مانند ضرب، باید ابتدا آنها را به کسر تبدیل کنیم. پس از تبدیل، تقسیم را به ضرب تبدیل کرده و کسر دوم را وارونه میکنیم. منظور از وارونه کردن، عوض کردن جای صورت و مخرج است. برای یادگیری بهتر این روش، یک مثال با هم حل میکنیم.
برای اینکه بیشتر با این روش آشنا شوید به مقاله آموزش تقسیم کسرها مراحعه کنید.
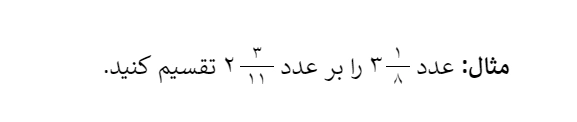
اولین کاری که باید انجام دهیم، تبدیل ابن اعداد به کسر است.
بعد از بهدست آوردن کسرها، تقسیم را به ضرب تبدیل کرده و کسر دوم را معکوس میکنیم.
پیشنهاد مطالعه: معکوس عدد مخلوط
نمونه سؤال عدد مخلوط کلاس چهارم با جواب
در این بخش، چند نمونه سؤال از عدد مخلوط کلاس چهارم با جواب را با هم حل میکنیم.
سؤال ۱: عدد مخلوط مربوط به شکل زیر را بنویسید و آن را به کسر تبدیل کنید.

جواب: در این تصویر، ۴ سیب کامل و نصف یا یکدوم یک سیب دیده میشود. بنابراین چهار و یکدوم سیب داریم و عدد مخلوط مربوط به آن را بهصورت زیر مینویسیم:
حالا باید این عدد را بهروشی که در این مقاله بیان کردیم، به کسر تبدیل کنیم.
سؤال ۲: دو عدد زیر را را از هم کم کنید و حاصل آن را بهصورت عدد مخلوط بنویسید.
و
جواب: همانطور که قبلاً اشاره کردیم، برای تفریق اعداد مخلوط، اعداد صحیح و اعداد کسری را جداگانه از هم کم میکنیم.
همانگونه میبینید، اعداد صحیح را میتوان از هم کم کرد اما اعداد کسری را خیر، زیرا صورت کسر دوم بزرگتر از صورت کسر اول است. البته این به این معنی نیست که عدد
از عدد
بزرگتر است. در چنین شرایطی، میتوانیم ابتدا اعداد مخلوط را به کسر تبدیل کنیم و سپس عمل تفریق را انجام دهیم.
اکنون با استفاده از روش گستردهنویسی، جواب بهدستآمده را به عدد مخلوط تبدیل میکنیم.
سؤال ۳: حاصل جمع زیر را محاسبه کنید.
جواب: عبارت اول یک عدد کامل است. بنابراین، آن را با قسمت صحیح عدد مخلوط جمع میکنیم و بخش کسری را بدون تغییر قرار میدهیم.
سؤال ۴: حاصل تفریق زیر را بهدست آورید.
جواب: ابتدا اعداد صحیح را از هم کم میکنیم.
۹ – ۷ = ۲
پس از کم کردن اعداد صحیح، اختلاف اعداد کسری را بهدست میآوریم. ازآنجا که مخرج دو کسر نامساوی هستند، ابتدا مخرج مشترک میگیریم و سپس عمل تفریق را انجام میدهیم.
کوچکترین مضرب مشترک ۲ و ۳ عدد ۶ است. بنابراین، خواهیم داشت:
درنتیجه
سخن پایانی
عدد مخلوط همانطور که از نامش پیداست، ترکیبی از دو عدد است: یک عدد کامل یا صحیح و یک عدد کسری. از این اعداد معمولاً برای فهم بهتر کسرهای بزرگتر از واحد استفاده میشود. کسر بزرگتر از واحد کسری است که مقدار صورتش از مقدار مخرج بزرگتر است. برای عدد مخلوط مانند سایر اعداد، میتوان چهار عمل ریاضی یعنی جمع، تفریق، ضرب و تقسیم را بهراحتی انجام داد. علاوهبر این، میتوانیم یک عدد مخلوط را به یک کسر یا یک عدد اعشاری هم تبدیل کنیم که در این آموزش روش انجام آن را همراه با مثال مفصل توضیح دادیم.
سؤالات متداول
- عدد مخلوط چیست؟
عدد مخلوط ترکیبی از دو عدد یعنی یک عدد کامل و یک عدد کسری است که با کمک آن میتوان کسرهای بزرگتر از واحد را بهتر درک کرد. - آیا میتوان یک عدد مخلوط را به کسر تبدیل کرد؟
بله. برای تبدیل عدد مخلوط به کسر کافیست عدد کامل را در مخرج کسر ضرب کنید و سپس، حاصل ضرب را با صورت کسر جمع بزنید. جواب بهدستآمده را در صورت قرار دهید و مخرج را همان مقدار مخرج عدد مخلوط بگذارید. - روش تبدیل عدد مخلوط به عدد اعشاری چگونه است؟
اگر بخواهیم یک عدد مخلوط را به عدد اعشاری تبدیل کنیم، باید صورت و مخرج بخش کسری عدد مخلوط را در عددی ضرب کنیم که مخرج آن ضریب ۱۰ شود. عدد کامل عدد مخلوط همان بخش صحیح عدد اعشاری و عدد کسری آن، همان بخش اعشاری عدد اعشاری خواهد بود. - جمع و تفریق اعداد مخلوط چگونه انجام میشود؟
اعداد صحیح و اعداد کسری دو عدد مخلوط را بهطور جداگانه جمع میزنیم یا از هم کم میکنیم. - حاصل ضرب و تقسیم اعداد مخلوط را چگونه بهدست آوریم؟
برای محاسبه ضرب و تقسیم اعداد مخلوط، ابتدا آنها را به کسر تبدیل میکنیم و سپس عمل ضرب یا تقسیم را انجام میدهیم.









