اعداد گنگ چه اعدادی هستند؟ | تفاوت با اعداد گویا

اعداد گنگ دنیای دیگری از اعداد هستند که گاهی اوقات با اعداد گویا اشتباه گرفته می‌شوند. این اعداد زمانی که به‌صورت عدد اعشاری نمایش داده می‌شوند، بخش اعشاری آن‌ها بدون تکرار تا بی‌نهایت ادامه می‌یابد. در این مقاله، می‌خواهیم اعداد گنگ در ریاضی و ویژگی‌های آن‌ها را معرفی کنیم و با آوردن مثال، نحوه تشخیص آن‌ها را آموزش دهیم.

اعداد گنگ چه اعدادی هستند؟

اعداد گنگ یا اعداد اصم مجموعه‌ای از اعداد حقیقی هستند که نمی‌توان آن‌ها را به‌صورت اعداد گویا بیان کرد. با توجه به آموزش‌های پیشین، اعداد گویا اعدادی هستند که به‌صورت کسری یعنیp/q ه در آن p و q اعداد صحیح و q≠0 است، نوشته می‌شوند. بنابراین، اعداد گنگ اعدادی حقیقی هستند که نمی‌توان آن‌ها را به‌صورت کسر ساده نشان داد. همچنین، در بسط اعشاری اعداد گنگ، رقم‌های اعشار آن‌ها بی‌نهایت و غیرمتناوب (تکرارناپذیر) است.به‌عنوان مثال، عددی مانند 1.6 را در نظر بگیرید. این عدد اعشاری تنها شامل یک رقم اعشاری است و می‌توان آن را به‌صورت یک کسر یعنی  ۸/۵ نوشت. اما عددی مانند۳√ که برابر با 1.73205… است، از رقم‌های اعشاری غیرمتناوب و نامحدود تشکیل شده است و نمی‌توان آن را به‌صورت کسر یا عدد گویا بیان کرد.

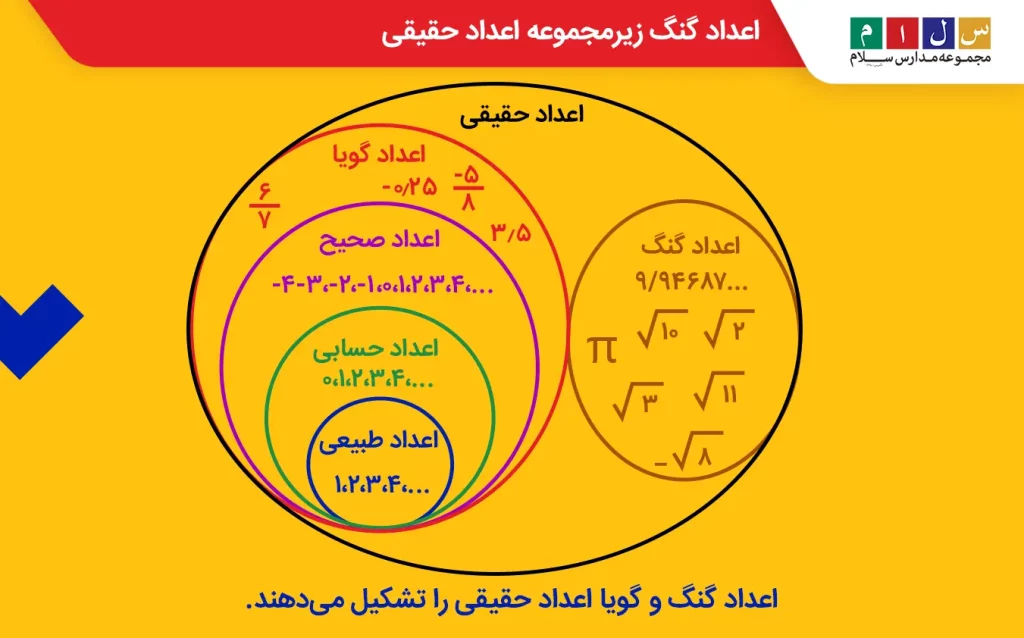
نماد اعداد گنگ

اعداد حقیقی (R) از اعداد گویا (Q) و اعداد گنگ تشکیل شده‌اند. بنابراین، می‌توان اعداد گنگ را با کم کردن اعداد گویا از اعداد حقیقی به‌دست آورد (R-Q). ازاین‌رو، نماد اعداد گنگ به انگلیسی به‌صورت Q’ نوشته می‌شود.

انواع اعداد گنگ

در این بخش، نمونه‌هایی از چند عدد گنگ خاص که معمولاً مورد استفاده قرار می‌گیرند را معرفی می‌کنیم. این اعداد عبارت‌اند از:

در حالت کلی، می‌توان گفت اعدادی که موارد زیر را شامل شوند، اعداد گنگ یا اصم محسوب می‌شوند.

ویژگی های اعداد گنگ

اعداد گنگ چند ویژگی دارند که در ادامه، به آن‌ها اشاره می‌کنیم.

$$\sqrt{۳}\times <!--\; \times \; -->\sqrt{۳}=۳$$ $$\sqrt{۳}+(۲-<!--\; -\; -->\sqrt{۳})=۲$$

همان‌طور که می‌بینید، حاصل هر دو عبارت یک عدد گویاست. این ویژگی نشان‌دهنده این است که مجموعه اعداد گنگ نسبت به عمل جمع و ضرب بسته نیستند.

اعداد گنگ روی محور

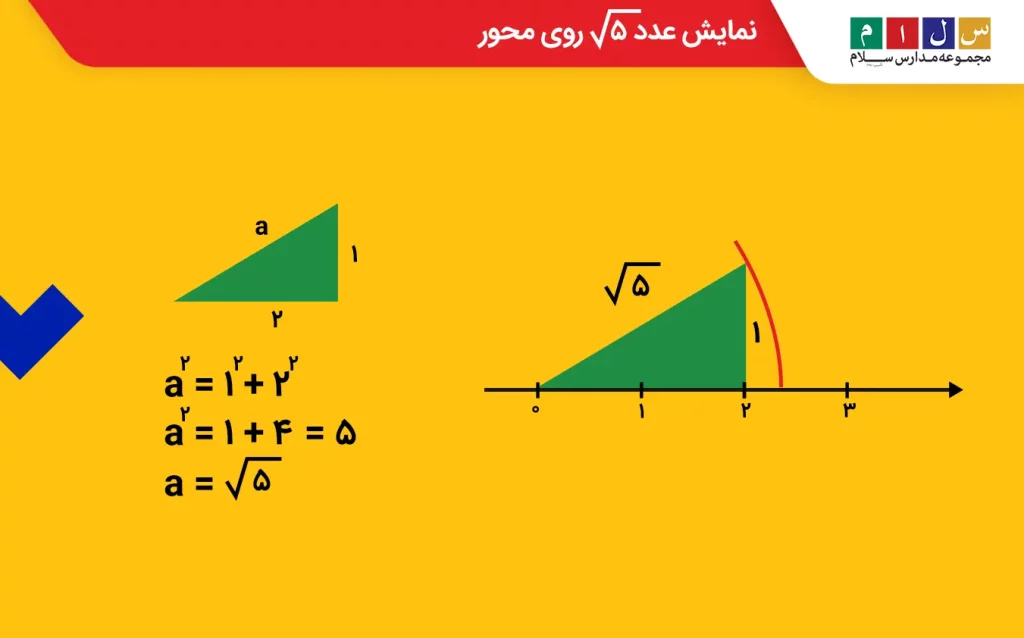
اعداد گنگ را می‌توان مانند سایر اعداد روی محور نشان داد. برای این کار کافی‌ست عدد موردنظر را به‌عنوان طول وتر یک مثلث قائم‌الزاویه در نظر بگیریم. به‌عنوان مثال، اگر بخواهیم عددی مانند۵√را روی محور نشان دهم، ابتدا مثلثی به‌شکل زیر تشکیل می‌دهیم که طول اضلاع آن در قضیه فیثاغورس صدق کند. با توجه به این توضیحات، می‌توان گفت۵√طول وتر مثلث قائم‌الزاویه‌ای است که اضلاع عمودبرهم آن برابر با ۲ و ۱ است.

مثلث موردنظر را روی محور به‌گونه‌ای قرار می‌دهیم که ضلع یک واحدی آن عمود بر محور باشد و گوشه دیگر مثلث روی مبدأ قرار گیرد. اکنون کمانی از یک دایره به مرکز صفر (مبدأ) و با شعاعی به‌اندازه وتر مثلث رسم می‌کنیم، طوری که کمان دایره با محور برخورد کند. نقطه برخورد کمان با محور، همان عدد گنگ متناظر یعنی ۲.۲۳۶ = ۵√ را نشان می‌دهد.

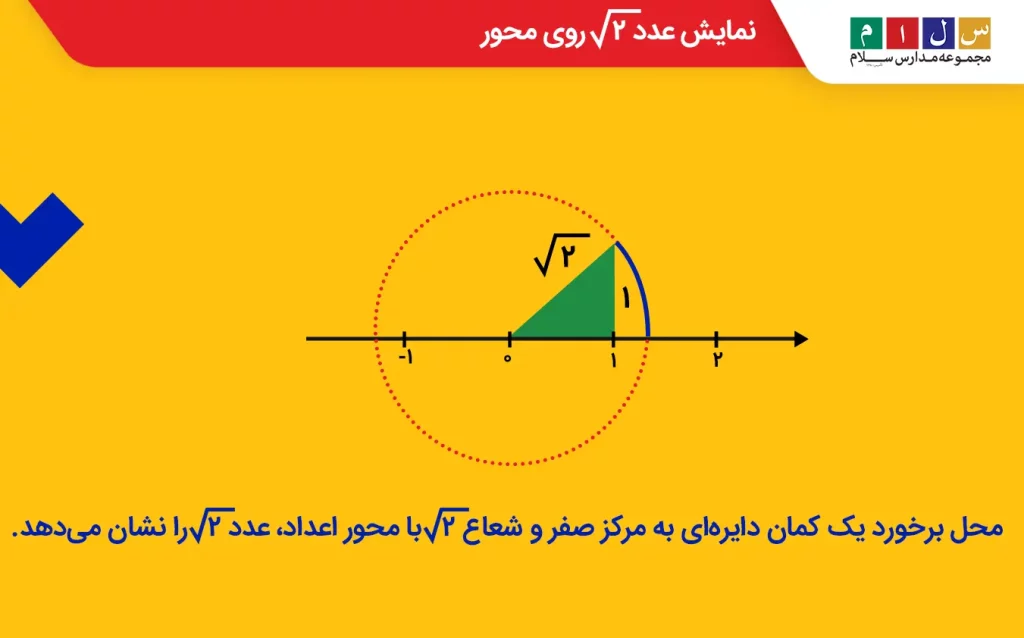
مثال: اعداد ۲√+و۲√-۱ را روی محور نشان دهید.
جواب: اعداد داده‌شده اعدادی گنگ هستند. بنابراین، با توجه به روشی که در بالا توضیح دادیم،۲√ را طول وتر مثلث قائم‌الزاویه‌ای در نظر می‌گیریم که طول اضلاع عمودبرهم آن برابر با یک است. بنابراین، کمانی که روی محور اعداد رسم می‌کنیم، باید دارای شعاعی به‌اندازه ۲√ باشد.

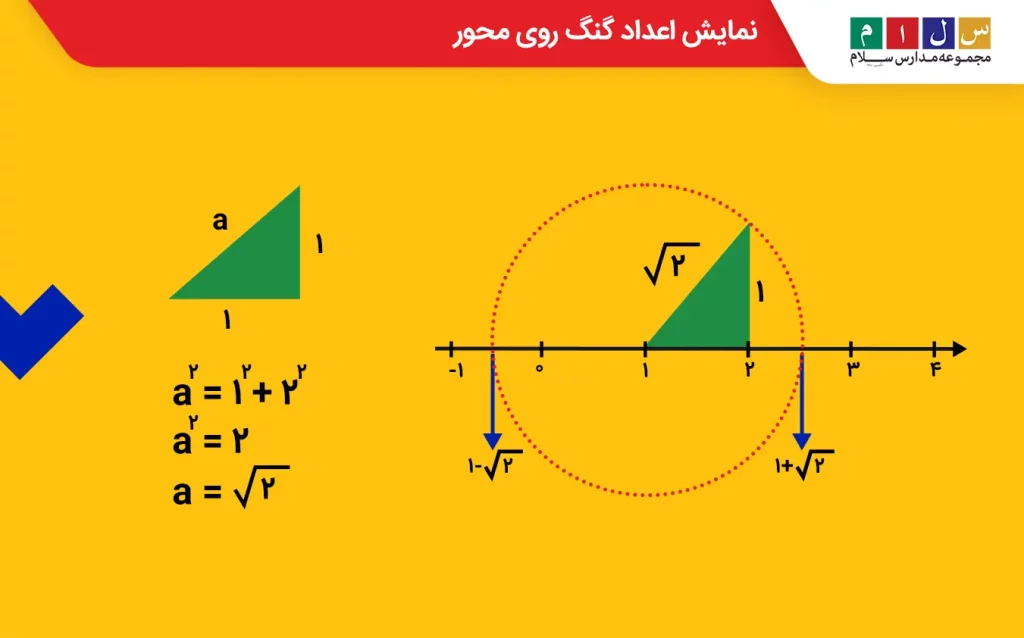
اکنون به سراغ اعداد ۲√+۱ و۲√-۱می‌رویم. عدد۲√+۱ یعنی اینکه یک واحد به ۲√ اضافه شده است. پس باید مثلث را مانند شکل زیر یک واحد به‌سمت راست محور انتقال دهیم و کمانی به شعاع ۲√ و مبدأ ۱ رسم کنیم تا محل برخورد آن با محور که نشان‌دهنده عدد ۲√+۱ است، مشخص شود. برای نشان دادن عدد ۲√-۱ نیز کافی‌ست همان کمان رسم‌شده را تا سمت چپ مثلث امتداد دهیم تا با محور اعداد برخورد کند. نقطه برخورد، عدد ۲√-۱ را نشان می‌دهد.

ازآنجا که۲√- قرینه۲√ است،۲√-۱ در سمت چپ نقطه ۲√+۱ قرار می‌گیرد.

برای نمایش اعداد گنگ روی محور اعداد باید دو نکته را در نظر بگیریم:

• اگر رادیکال مثبت باشد، کمان دایره را سمت راست رسم می‌کنیم، اما اگر پشت رادیکال علامت منفی باشد، مثلث قرینه شده و کمان را سمت چپ می‌زنیم.

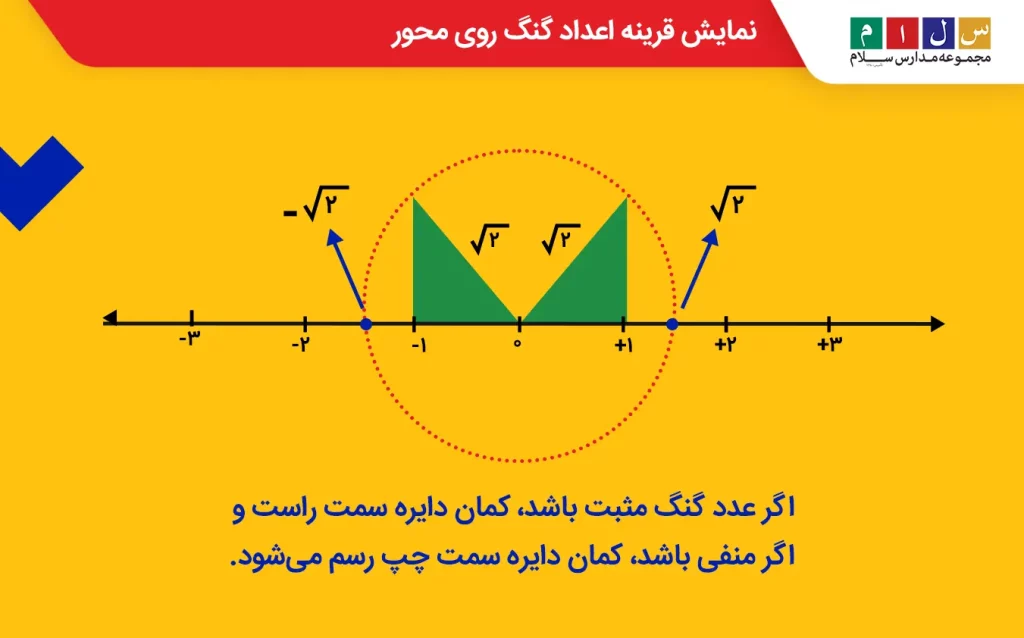
اگر یک عدد صحیح به عدد گنگ اضافه شود، مرکز کمان رسم‌شده همان عدد صحیح خواهد بود. 

روش به دست آوردن اعداد گنگ

اگر بخواهیم بین دو عدد مثلاً ۳ و ۴ یک عدد گنگ به‌دست آوریم، اولین کاری که باید انجام دهیم این است که دو عدد را به توان دو برسانیم و آن‌ها را زیر رادیکال قرار دهیم. یعنی عدد ۳ و ۴ را به‌ترتیب به‌صورت ۹ √و ۱۶√ بنویسیم. اکنون می‌توانیم بین این دو عدد، اعدادی را که جذر کامل ندارند به‌عنوان عدد گنگ انتخاب کنیم. برای مثال، ۱۳√ و ۱۰√ دو عدد گنگ هستند که اگر با ماشین‌حساب جذر آن‌ها را بگیرید، حاصل آن‌ها عددی بین ۳ و ۴ با ارقام اعشاری نامتناهی و غیرمتناوب خواهد بود.

تفاوت اعداد گنگ و اعداد گویا

جدول زیر، تفاوت بین اعداد گنگ و گویا را نشان می‌دهد.

اعداد گنگ	اعداد گویا
نمی‌توان آن‌ها را به‌صورت کسری یا نسبت بیان کرد.	به‌صورت کسری یا نسبت بیان می‌شوند.
رقم‌های اعشاری نامتناهی و پایان‌ناپذیر هستند.	رقم‌های اعشاری می‌تواند متناهی باشد.
الگوی مشخصی در رقم‌های اعشاری وجود ندارد.	رقم‌های اعشاری درصورت نامتناهی بودن دارای الگوی تکراری است.
مثال: ۱۳√، π و e	مثال: ۰.۳۳۳۳۳، ۰.۶۵۶۵۶۵ و ۱.۷۵

مثال اعداد گنگ

مثال ۱: کدام یک از اعداد زیر، گنگ و کدام یک گویا هستند؟

√۵, ۲, √۱۱, ۳.۵۶, ۱.۳۳۳۳…, ۱۰۰, ۴.۵۳۴۶۷۸۲

جواب: با توجه به تعریف و تفاوت اعداد گنگ و گویا این اعداد به‌صورت زیر تقسیم‌بندی می‌شوند:

اعداد گنگ : ….۵۳۴۶۷۸۲ , ۱۱√ , ۵√ , ۴

اعداد گویا: ۲,۳.۵۶,۱۰۰,۱.۳۳۳۳

مثال ۲: آیا حاصل‌جمع اعداد ۳√ + ۲ و ۳√-۳ عددی گنگ است؟

۲+ √۳+ √۳-۳=۲+۳+√۳-۳=۵

بنابراین، پاسخ به‌دست‌آمده یک عدد گویاست.

سخن پایانی

اعداد گنگ یا اصم اعدادی غیرگویا با ارقام اعشاری نامتناهی و غیرمتناوب هستند که ازجمله معروف‌ترین این اعداد می‌توان عدد π را نام برد. این اعداد را نمی‌توان مانند اعداد گویا به‌صورت کسری یا نسبت بیان کرد. همچنین، اعداد گنگ نسبت به عمل جمع و ضرب بسته نیستند؛ یعنی اگر دو عدد گنگ را با هم جمع یا در هم ضرب کنیم، ممکن است حاصل آن‌ها عدد گنگ نباشد. اعداد گنگ را مانند دیگر اعداد می‌توان روی محور نمایش داد که در این مقاله، مراحل و نکات آن را با جزئیات به‌همراه مثال توضیح دادیم. پیشنهاد ما این است برای تسلط بیشتر بر نحوه مشخص کردن اعداد گنگ روی محور، مثال‌های بیشتری حل کنید تا این روش را عمیق‌تر فراگیرید.

سؤالات متداول

1. عدد گنگ چه عددی است؟
   عدد گنگ به اعدادی گفته می‌شود که نمی‌توان آن‌ها را به‌صورت کسری نوشت. این اعداد، گویا نیستند و ارقام اعشاری آن‌ها نامحدود غیرمتناوب است.
2. اعداد گنگ را با چه حرفی نشان می‌دهند؟
   اعداد گنگ با حرف Q’ نشان داده می‌شوند.
3. آیا اعداد گنگ زیرمجموعه اعداد گویا هستند؟
   خیر، اعداد گنگ زیرمجموعه اعداد گویا نیستند و با هم متفاوت‌اند.
4. چگونه بین دو عدد گنگ عدد گویا بنویسیم؟
   ابتدا دو عدد گنگ را به اعداد اعشاری تبدیل کرده و سپس، به‌دلخواه بین آن‌ها اعداد گویا انتخاب می‌کنیم. بین دو عدد گنگ بی‌نهایت عدد گویا وجود دارد.
5. چگونه بین دو عدد رادیکالی عدد گنگ بنویسیم؟
   بین دو عدد رادیکالی، عددی که جذر کامل نداشته باشد و حاصل آن برابر با یک عدد اعشاری با ارقام اعشاری نامتناهی و غیرمتناوب شود، عددی گنگ خواهد بود.