فهرست مطالب
Toggleب م م یا بزرگترین مقسومعلیه مشترک را معمولاً زمانی که میخواهیم ساده کردن کسر را انجام دهیم، بسیار بهکار میبریم. در این آموزش قصد داریم روشهای تعیین ب م م اعداد را همراه با حل نمونه سؤال آموزش دهیم. پس اگر میخواهید این روشها را بیاموزید، با ادامه این مطلب همراه ما باشید.
بزرگترین مقسومعلیه مشترک یا ب م م چیست؟
ب م م مخفف بزرگترین مقسومعلیه مشترک است. برای محاسبه ب م م دو یا چند عدد مقسومعلیههایی را که بین آن اعداد مشترک است، تعیین کرده و بزرگترین آنها را مشخص کنیم.
فرمول ب م م هم به صورت زیر است:
(a × b) ÷ [a, b] = |a × b|
بهعنوان مثال، اگر بخواهیم ب م م اعداد ۲۴ و ۳۰ را تعیین کنیم، ابتدا مقسومعلیههای آنها را مینویسیم:
- مقسومعلیههای ۲۴: ۱، ۲، ۳، ۴، ۶، ۸، ۱۲، ۲۴
- مقسومعلیههای ۳۰: ۱، ۲، ۳، ۵، ۶، ۱۰، ۱۵، ۳۰
همانطور که میبینید، اعداد ۱، ۲، ۳، و ۶ مقسومعلیههای مشترک ۲۴ و ۳۰ هستند که از میان آنها عدد ۶ از بقیه بزرگتر است. بنابراین، ب م م یا بزرگترین مقسومعلیه مشترک اعداد ۲۴ و ۳۰ عدد ۶ است و آن را بهصورت زیر نشان میدهند:
( ۲۴ , ۳۰ ) = ۶
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
مقسوم علیه یا شمارنده چیست؟
برای یادگیری ب م م، لازم است مفهوم مقسومعلیه مشترک را یاد بگیرید.
مقسومعلیه که به آن عامل یا شمارنده نیز گفته میشود، عددی است که عدد دیگر بر آن تقسیم شده و باقیمانده نیز صفر شده است.
بهعبارت دیگر، مقسومعلیه یا عامل اعدادی هستند که در هم ضرب میشوند تا یک عدد بهدست آید. برای مثال، وقتی میگوییم مقسومعلیههای عدد ۲۰ منظورمان اعدادی است که ۲۰ بر آنها بخشپذیر است. عاملهای عدد ۲۰ عبارتاند از:
۱, ۲, ۴, ۵, ۱۰, ۲۰
پیشنهاد مطالعه: کوچکترین مضرب مشترک یا ک م م چیست؟
بزرگترین مقسومعلیه مشترک چگونه تعیین می شود؟
ب م م دو یا چند عدد را میتوان از دو روش زیر تعیین کرد:
- لیست کردن عاملها
- تجزیه به عاملهای اول
در ادامه هر دو روش را با مثال توضیح خواهیم داد.
تعیین بزرگترین مقسومعلیه مشترک با لیست کردن عامل ها
در این روش، عاملهای اعداد را لیست کرده و آنهایی را که مشترک هستند، مشخص میکنیم. سپس، عامل مشترکی که از همه بزرگتر است را بهعنوان ب م م انتخاب میکنیم.
مثال: ب م م اعداد ۱۸ و ۲۷ را بیابید.
ابتدا مقسومعلیههای ۱۸ و ۲۷ را لیست کرده و بهصورت زیر مینویسیم:
- مقسومعلیههای ۱۸: ۱، ۲، ۳، ۶، ۹، ۱۸
- مقسومعلیههای ۲۷: ۱، ۳، ۹، ۲۷
عاملهای ۱، ۳ و ۹ در هر دو عدد ۱۸ و ۲۷ مشترک است که از بین آنها عامل ۹ از بقیه بزرگتر است. پس بزرگترین عامل مشترک یا ب م م ۱۸ و ۲۷ عدد ۹ است.
تعیین بزرگترین مقسومعلیه مشترک (ب م م) از راه تجزیه به عامل های اول
یافتن بزرگترین مقسومعلیه مشترک با روش لیست کردن اگرچه روش آسانی بهنظر میرسد اما برای اعداد بزرگتر ممکن است دشوار باشد. در چنین مواقعی استفاده از روش تجزیه راهکار مناسبی خواهد بود.
اگر بخواهیم ب م م دو یا چند عدد را با روش تجزیه بهدست آوریم، بهصورت زیر عمل میکنیم:
- ابتدا اعداد موردنظر را بهصورت حاصلضرب عاملهای اول مینویسیم.
- سپس عاملهای اول مشترک را مشخص کرده و آنها را در هم ضرب میکنیم تا مقدار ب م م بهدست آید.
برای درک بهتر این روش به مثال زیر توجه کنید.
مثال: ب م م اعداد ۶۰ و ۹۰ را با روش تجزیه تعیین کنید.
برای تعیین ب م م این دو عدد با روش گفتهشده کافیست ابندا آنها را بهصورت زیر به عاملهای عدد اول تجزیه میکنیم:
۶۰=۲ × ۳ × ۵ × ۲
۹۰= ۲× ۳ × ۵× ۳
حالا عاملهای هر دو را بررسی کرده و آنهایی را که در هر دو مشترکاند با کشیدن دایره دور آنها مانند تصویر زیر مشخص میکنیم. در آخر عاملهای مشترک را در هم ضرب کرده و حاصل آن را بهدست میآوریم. حاصلضرب مقدار ب م م را به ما خواهد داد. با این توضیحات بزرگترین عامل مشترک ۶۰ و ۹۰ مساوی است با:
( ۶۰, ۹۰ ) = ۲ × ۳ × ۵ = ۳۰

فرمول ب م م برای سه عدد یا بیشتر از راه تجزیه، به همین صورت است و باید همین مراحل را دنبال کرد. در بخش بعدی، چند نمونه سؤال از نحوه محاسبه ب م م حل میکنیم تا این مبحث را عمیقتر یاد بگیرید.
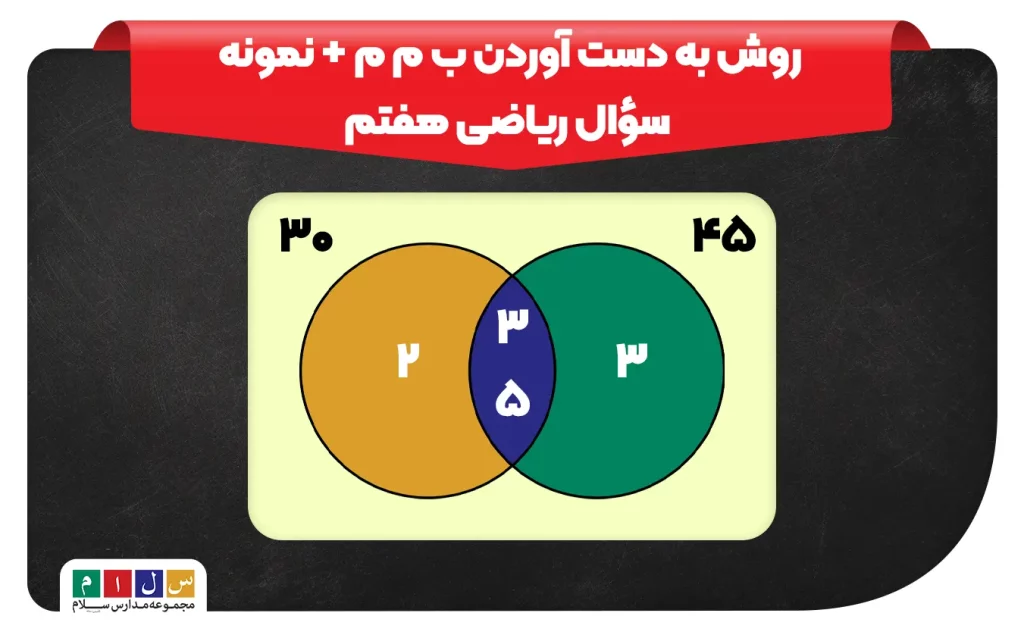
نمونه سؤال محاسبه ب م م ریاضی هفتم
ب م م اعداد زیر را را به روش تجزیه بهدست آورید.
- ( ۴۰, ۶۰ )
- ( ۴۲, ۵۶ )
- ( ۱۶, ۲۰, ۳۶ )
جواب: برای مشخص کردن ب م م این اعداد ابتدا آنها را بهصورت حاصلضرب اعداد اول مینویسیم، سپس عاملهای مشترک بین هر دو یا هر سه عدد را در هم ضرب میکنیم.
- اعداد ۴۰ و ۶۰ را بهصورت زیر تجزیه میکنیم:
۴۰ = ۲× ۲× ۲×5
۶۰ = ۲ × ۲ × ۳ × ۵
میبینیم که عامل ۲ با دو بار تکرار و عامل ۵ با یک بار تکرار در هر دو عدد ۴۰ و ۶۰ مشترک است. بنابراین، ب م م آنها برابر است با:
( ۴۰, ۶۰ ) = ۲ × ۲×۵ = ۲۰
۲.ابتدا باید اعداد ۴۲ و ۵۶ را به عاملهای اول تجزیه کنیم:
۴۲ = ۲ × ۳ × ۷
۵۶ = ۲ × ۲× ۲× ۷
همانطور که مشاهده میکنید، عدد ۲ و ۷ عاملهای مشترک ۴۲ و ۵۶ هستند. توجه داشته باشید که اگرچه عامل ۲ در ۵۶ سه بار تکرار شده، اما در عدد ۴۲ این عامل تنها یک بار تکرار شده است و از این رو، عامل ۲ با حداقل یک بار تکرار در هر دو عدد باید بهعنوان عامل مشترک آنها در نظر گرفته شود. پس خواهیم داشت:
( ۴۲, ۵۶ ) = ۲ × ۷ = ۱۴
۳.در این سؤال بهجای دو عدد باید ب م م سه عدد را بهدست آوریم. همانطور که قبلاً هم گفتیم، روش تعیین ب م م سه عدد مانند روش تعیین ب م م دو عدد است، با این تفاوت که در اینجا باید عاملهای مشترک سه عدد را بیابیم. بنابراین، داریم:
۱۶ = ۲ × ۲ × ۲
۲۰ = ۲ × ۲× ۵
۳۶ = ۲ × ۲ × ۳ × ۳
بین هر سه عدد تنها عامل ۲ با دو بار تکرار مشترک است. پس ب م م آنها مساوی است با
( ۱۶, ۲۰, ۳۶ )= ۲ × ۲ = ۴
سخن پایانی
در این مقاله یاد گرفتیم که منظور از ب م م دو یا چند عدد بزرگترین مقسومعلیه مشترک بین آنها است که با روش لیست کردن عاملها یا تجزیه به عاملها اول قابل محاسبه است. مفهوم ب م م در ساده کردن کسرها بسیار کاربرد دارد. بنابراین، توصیه میشود با حل تمرینهای متعدد تسلط خود را در این مبحث بیشتر کنید تا در محاسبات مربوط به کسرها کمتر با مشکل مواجه شوید.