فهرست مطالب
Toggleاصطلاح نسبت را معمولا برای مقایسه اندازه یا مقدار دو چیز بهکار میبرند. بهعنوان مثال، زمانی که یک قناد میخواهد کیک یا کلوچه بپزد، ابتدا نسبت مواد اولیه را میسنجد. اگر همین قناد بخواهد کیک یا کلوچه بزرگتری بپزد باید با حفظ همان نسبت، مواد اولیه بیشتری استفاده کند. این تنها یکی از کاربردهای نسبت در زندگی روزمره است. اگر میخواهید با مفهوم نسبت در ریاضی و نسبت های مساوی بیشتر آشنا شوید، پیشنهاد میکنیم این آموزش را دنبال کنید.
نسبت در ریاضی چیست؟
نسبت در ریاضی یعنی مقایسه بین دو کمیت مختلف از یک نوع با واحدهای یکسان. بهبیان سادهتر، نسبت اصطلاحی است که برای مقایسه دو یا چند عدد بهکار میرود و برای نشان دادن اینکه یک مقدار درمقایسه با مقدار دیگر چقدر بزرگ یا کوچک است استفاده میشود. در یک نسبت، دو کمیت با استفاده از تقسیم مقایسه میشوند. کمیت اول نسبت را صورت و کمیت دوم آن را مخرج میگویند و نسب این دو به هم را تناسب در ریاضی می گویند.
برای مثال، فرض کنید در یک ظرف میوه ۵ عدد سیب و ۷ عدد پرتقال وجود دارد؛ اگر بخواهیم تعداد سیب و پرتقال را با هم مقایسه کنیم، میگوییم نسبت سیب به پرتقال ۵ به ۷ است و آن را با عبارت کسری زیر نشان میدهیم.
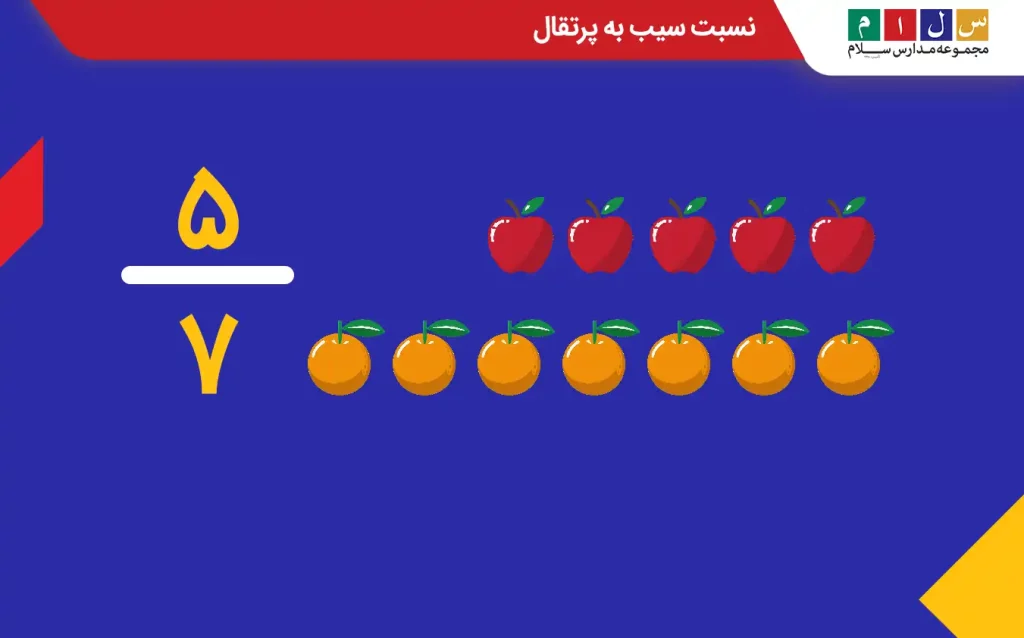
درادامه، دو مثال حل میکنیم تا مفهوم نسبت در ریاضی را بهتر درک کنید.
مثال ۱: در شکل زیر نسبت تعداد مربعها را به تعداد کل شکلها بهدست آورید.

جواب: شکل دادهشده شامل ۴ مربع و ۳ دایره است؛ یعنی درمجموع ۷ شکل در تصویر دیده میشود. بنابراین، نسبت تعداد مربعها به تعداد کل شکلها ۴ به ۷ یا همان ۴۷ است.
مثال ۲: نسبت مساحت قسمت رنگشده به مساحت قسمت رنگنشده و نسبت مساحت قسمت رنگشده به مساحت کل شکل را تعیین کنید.

پیشنهاد مطالعه: تبدیل کسر به اعشار به زبان ساده
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
نسبت های مساوی چیست؟
شکلهای نشانداده در تصویر زیر را بدون توجه به نسبتهای آنها نگاه کنید. همانطور که میبینید، هر سه شکل نصف یک پیتزای کامل را نشان میدهند و تفاوتی با هم ندارند. تنها تفاوت آنها این است که هرچه پیتزا به تکههای بیشتری تقسیم میشود، اعداد صورت و مخرج بزرگتر میشوند. صورت کسر، تعداد تکههای پیتزا و مخرج آن، تعداد تکههای یک پیتزای کامل را نشان میدهد.

پیشنهاد مطالعه: انجام راحت محاسبات با جمع و تفریق فرایندی
چگونه نسبت های مساوی را به دست آوریم؟
همانطور که در بخش قبل هم اشاره کردیم، دو یا چند نسبت که مقدار یکسانی داشته باشند را نسبت های مساوی میگوییم. برای بهدست آوردن نسبت های مساوی، دو کمیت یا همان صورت و مخرج نسبت را در یک عدد غیرصفر ضرب یا بر آن تقسیم میکنیم. بهعنوان مثال، فرض کنید ۶ مهره قرمز و ۸ مهره سبز داریم. نسبت تعداد مهرههای قرمز به تعداد مهرههای سبز ۶ به ۸ یا ۶۸ است. اگر صورت و مخرج این نسبت را یک بار در دو ضرب و بار دیگر بر دو تقسیم کنیم، دو نسبت مساوی برای آن بهدست خواهد آمد. شکل زیر را ببینید تا بهتر متوجه شوید.
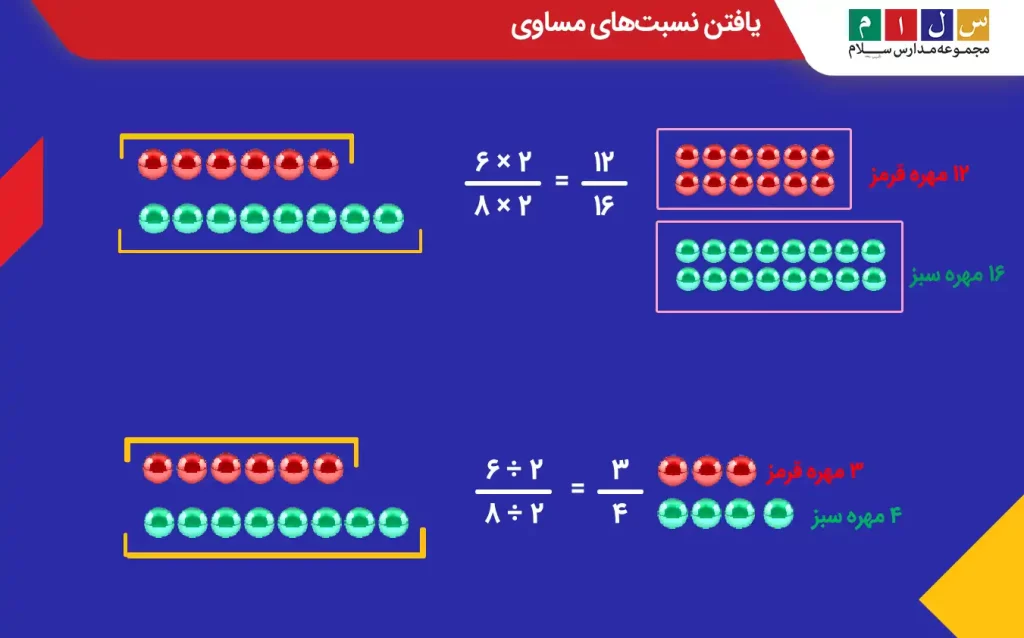
بنابراین، سه نسبت مساوی بهشکل زیر خواهیم داشت:
پیشنهاد مطالعه: آموزش طرفین وسطین به زبان ساده
یافتن نسبت های مساوی با شکل
با استفاده از شکل هم میتوان نسبت های مساوی را بهدست آورد. البته، استفاده از شکل برای اعداد کوچک مناسب است و برای اعداد بزرگ وقتگیر و دشوار خواهد بود.برای مثال، اگر بخواهیم برای پر کردن جاهای خالی در تساوی زیر و یافتن نسبت های مساوی ۱۳ از شکل استفاده کنیم، باید بهصورت زیر عمل کنیم.
مرحله اول: ابتدا کسر
را با شکل نشان میدهیم. برای این کار، یک شکل دلخواه مثل مستطیل را به سه قسمت مساوی تقسیم میکنیم و یک قسمت از سه قسمت را رنگ میزنیم.

مرحله دوم: برای اینکه مشخص شود نسبت ۱ به ۳ برابر با نسبت چه عددی به ۶ است، شکل را به ۶ قسمت مساوی تقسیم میکنیم.

همانطور که میبینید، قسمت رنگشده تغییری نکرده و تنها به دو قسمت کوچکتر تقسیم شده است. بنابراین، طبق شکل بالا ۲ قسمت از ۶ قسمت رنگ شده و درنتیجه صورت کسر برابر با ۲ است.
مرحله سوم: در نسبت سوم چون مقدار صورت یا بهعبارتی تعداد خانههای رنگشده برابر با ۴ است، باید کل شکل را طوری تقسیم کنیم که قسمت رنگشده به ۴ قسمت مساوی تقسیم شود و مشخص گردد نسبت ۴ به چه عددی برابر با نسبت ۱ به ۳ یا ۲ به ۶ است.
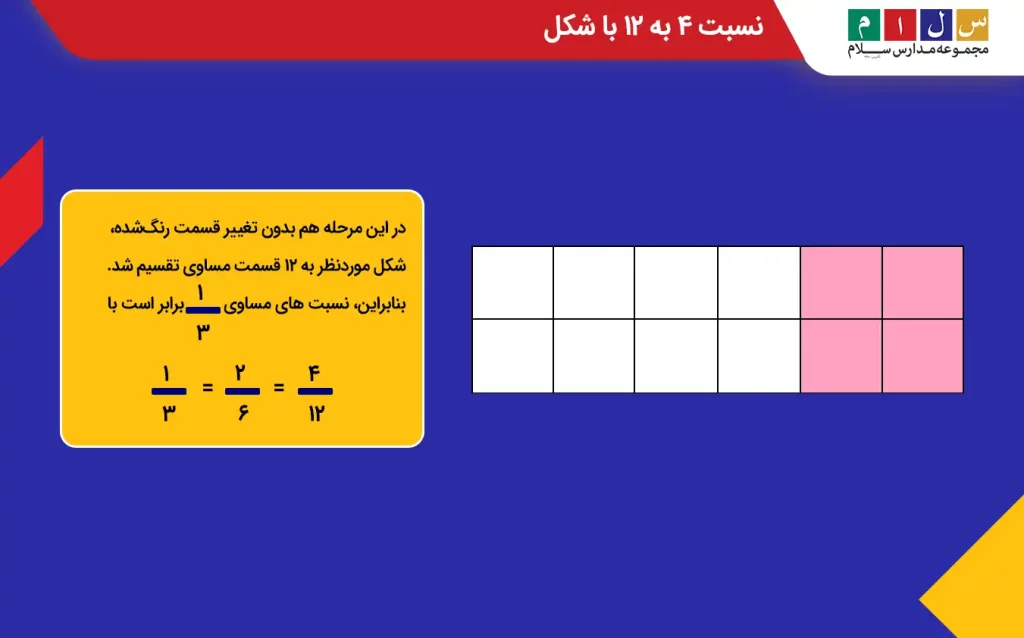
در این مرحله هم بدون تغییر قسمت رنگشده، شکل موردنظر به ۱۲ قسمت مساوی تقسیم شد. بنابراین، نسبت های مساوی ۱۳ برابر است با
بدون شکل هم میتوانستیم نسبت های مساوی را برای ۱۳ بهدست آوریم، چون همانطور که گفته شد، نسبت های مساوی از ضرب صورت و مخرج در یک عدد یا تقسیم آنها بر یک عدد بهدست میآیند. در اینجا هم میتوانیم از این روش استفاده کنیم. مثلاً میگوییم ۳ در چه عددی ضرب شده که حاصلش برابر با ۶ است. همان عدد را در صورت هم ضرب میکنیم تا مقدار صورت بهدست آید. برای نسبت دوم هم به همین روش عمل میکنیم:
نمونه سؤال نسبت های مساوی کلاس پنجم
در این بخش، نمونه سؤالهای مختلفی را از نسبت های مساوی حل میکنیم.
سؤال ۱: دو مثلث متساویالاضلاع داریم. طول ضلع مثلث کوچکتر ۱۴ سانتیمتر و طول ضلع مثلث بزرگتر ۲۰۰ میلیمتر است. نسبت طول ضلع مثلث کوچکتر به طول ضلع مثلث بزرگتر چقدر است؟
جواب: طبق تعریفی که در ابتدای مقاله داشتیم، برای بهدست آوردن نسبت، دو کمیت باید واحد یکسانی داشته باشند. پس باید ابتدا واحد طول ضلع مثلث بزرگتر را به سانتیمتر تبدیل کنیم. میدانیم که هر سانتیمتر برابر با ۱۰ میلیمتر است، پس ۲۰۰ میلیمتر معادل ۲۰ سانتیمتر خواهد بود.
پس نسبت طول ضلع مثلث کوچکتر به طول ضلع مثلث بزرگتر ۱۴ به ۲۰ یا:
خواهد بود. ازآنجا که مقادیر صورت و مخرج بر ۲ بخشپذیرند، میتوان این نسبت را سادهتر کرد و بهشکل زیر نوشت:
سؤال ۲: آیا نسبتهای
مساوی هستند؟
جواب: کسر بزرگتر را تا جای ممکن ساده میکنیم تا مشخص شود آیا این دو نسبت با هم مساویاند یا نه.
نسبت مساوی
برابر است با
نه
بنابراین، دو نسبت دادهشده در صورت سؤال، نسبت های مساوی نیستند.
سؤال ۳: چهار نسبت مساوی با
را بهدست آورید.
جواب: برای بهدست آوردن چهار نسبت مساوی با کسر
کافیست صورت و مخرج آن را در چهار عدد دلخواه غیرصفر ضرب کنید.
بنابراین، نسبتهای زیر را میتوان مساوی دانست:
سؤال ۴: در جای خالی چه عددی قرار گیرد تا دو نسبت مساوی باشند؟
جواب: ابتدا باید ببینیم ۴۲ بر چه عددی تقسیم شده که حاصل آن ۷ شده است. سپس، صورت را نیز بر همان عدد تقسیم کنیم.
پیشنهاد مطالعه: اعداد اعشاری – عدد مخلوط – تبدیل کسر به عدد مخلوط
سخن پایانی
در ریاضی، برای مقایسه دو یا چند عدد و بزرگ یا کوچک بودن مقدار آنها درمقایسه با یکدیگر از اصطلاح نسبت استفاده میشود. اگر صورت و مخرج یک نسبت را در یک عدد غیرصفر ضرب یا بر آن تقسیم کنیم، نسبتی مساوی با آن نسبت بهدست خواهد آمد. چنین نسبتهایی را نسبت های مساوی مینامند. بنابراین، میتوان گفت نسبت های مساوی نسبتهایی هستند که مقدار یکسانی دارند. میانگین هم مثل نسبتهای مساوی از مباحث ریاضی پنجم دبستان است، پس پیشنهاد میکنیم مقاله میانگین چیست را هم مطالعه کنید.
سؤالات متداول
- نسبت در ریاضی چیست؟
نسبت اصطلاحی است که برای مقایسه دو یا چند عدد بهکار میرود و زمانی از آن استفاده میشود که بخواهیم بزرگ یا کوچک بودن یک مقدار را درمقایسه با مقدار دیگر نشان دهیم. - نسبت مساوی یعنی چه؟
اگر دو یا چند نسبت مقدار یکسانی داشته باشند، آنها را نسبت های مساوی میگوییم. - نسبت های مساوی را چگونه بهدست آوریم؟
برای بهدست آوردن نسبت های مساوی با یک نسبت، باید صورت و مخرج آن نسبت را در عددی غیرصفر ضرب یا بر آن تقسیم کنیم.









