فهرست مطالب
Toggleهنگام اندازهگیری طول، وزن، زمان، دما و غیره ممکن است با اعدادی مواجه شویم که بین اعداد صحیح یا کامل قرار میگیرند. در چنین مواردی، برای نمایش عدد موردنظر باید از اعدادی استفاده کرد که مقدار دقیق را به ما نشان دهند. این اعداد همان اعداد اعشاری هستند که در این مقاله قصد داریم آنها را معرفی کرده و چهار عمل جمع، تفریق، ضرب و تقسیم در آنها را با حل مثال توضیح دهیم. عدد مخلوط را نیز بخوانید.
اعداد اعشاری چیست؟
اعداد اعشاری اعدادی هستند که بین دو عدد کامل یا صحیح قرار دارند. میتوان گفت که اعداد اعشاری روش دیگری برای نشان دادن کسرها هستند. برای مثال، تصویر زیر را در نظر بگیرید. شکل (۱) ۱۷ مربع کامل را نشان میدهد. در شکل (۲) یکی از این مربعها به ۱۰ قسمت مساوی تقسیم شده و ۴ قسمت از ۱۰ قسمت آن رنگ شده است. در شکل (۳) نیز همین مربع به ۱۰۰ قسمت مساوی تقسیم شده و ۸ قسمت از ۱۰ قسمت آن رنگی است. بنابراین، در این تصویر ۱۷ مربع کامل، ۴ تا یکدهم و ۸ تا یکصدم وجود دارد. تعداد مربعهای کامل را با کمک ممیز (/) جدا میکنیم و عدد مربوط به شکل زیر را بهصورت ۱۷/۴۸ مینویسیم. این عدد را میخوانیم هفده و چهلوهشت صدم. در زبان انگلیسی بهجای (/) از نقطه (.) استفاده میکنند.
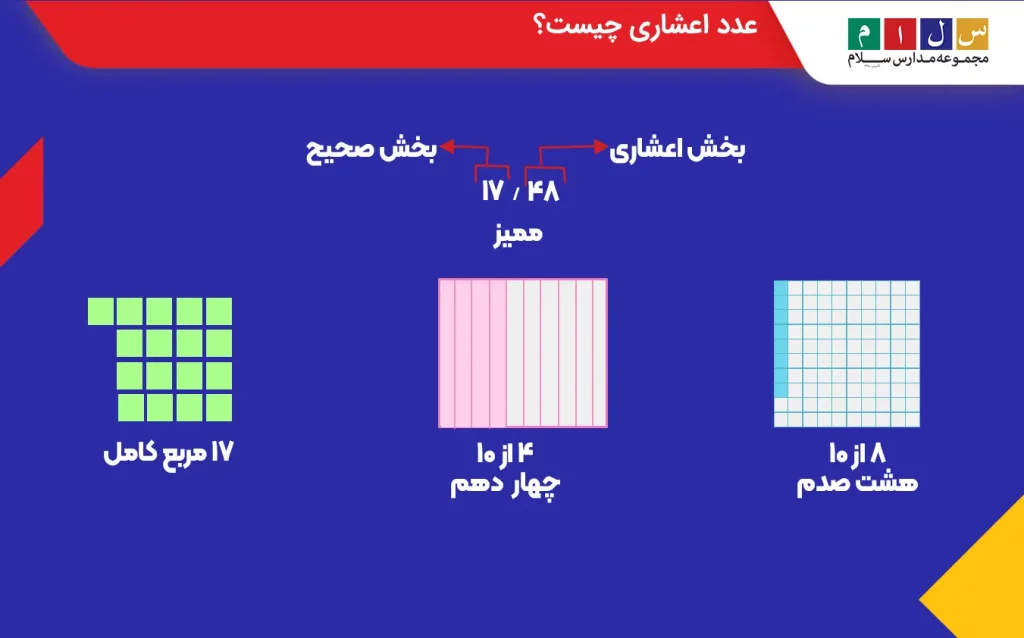
اعداد سمت چپ ممیز را بخش صحیح و اعداد سمت راست ممیز را بخش اعشاری میگویند. درواقع، ممیز برای جدا کردن بخش صحیح از بخش اعشاری بهکار میرود. در اینجا ۱۷، بخش صحیح و ۴۸، بخش اعشاری عدد ۱۷/۴۸ است.
پس با توجه به توضیحاتی که دادیم، میتوان گفت عدد اعشاری عددی است که از دو بخش صحیح و بخش اعشاری تشکیل شده است. بخش صحیح نشاندهنده اعداد کامل و بخش اعشاری نشاندهنده اعداد کمتر از یک است.
پیشنهاد مطالعه: آموزش طرفین وسطین به زبان ساده
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
ارزش مکانی اعداد اعشاری
معمولاً دانشآموزان در بخش اعداد اعشاری چهارم دبستان با ارزش مکانی این اعداد آشنا میشوند. بهطور کلی، برای نوشتن و خواندن اعداد اعشاری به حروف لازم است ابتدا با ارزش مکانی این اعداد آشنا شویم. یادگیری ارزش مکانی اعداد اعشاری در یادگیری مفاهیم پیچیدهتری مانند نحوه محاسبه درصد کمک زیادی به دانشآموزان میکند. شکل زیر ارزش مکانی اعداد اعشاری را نشان میدهد.
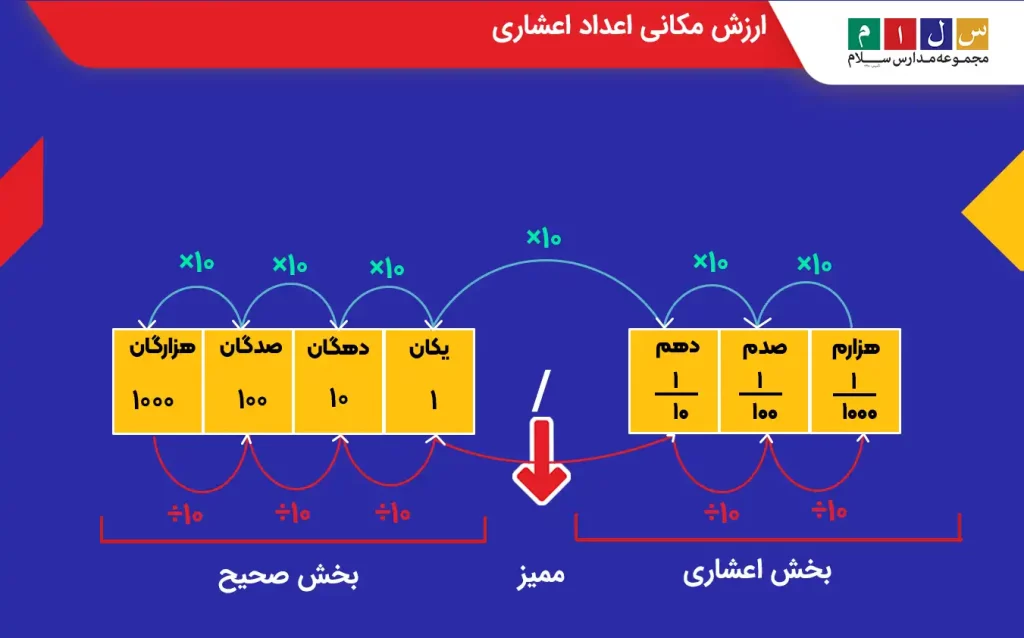
همانطور که میبینید، هرچه بهسمت راست میرویم، ارزش اعداد نسبت به عدد قبلی بهاندازه ۱۰ کم میشود و برعکس، هرچه بهسمت چپ حرکت میکنیم، ارزش اعداد نسبت به عدد قبلی ۱۰ برابر بیشتر میشود. برای آشنایی بیشتر با ارزش مکانی اعداد اعشاری، اعداد نوشتهشده در جدول زیر را بررسی میکنیم.
پیشنهاد مطالعه: نسبت های مساوی را چگونه به دست آوریم؟
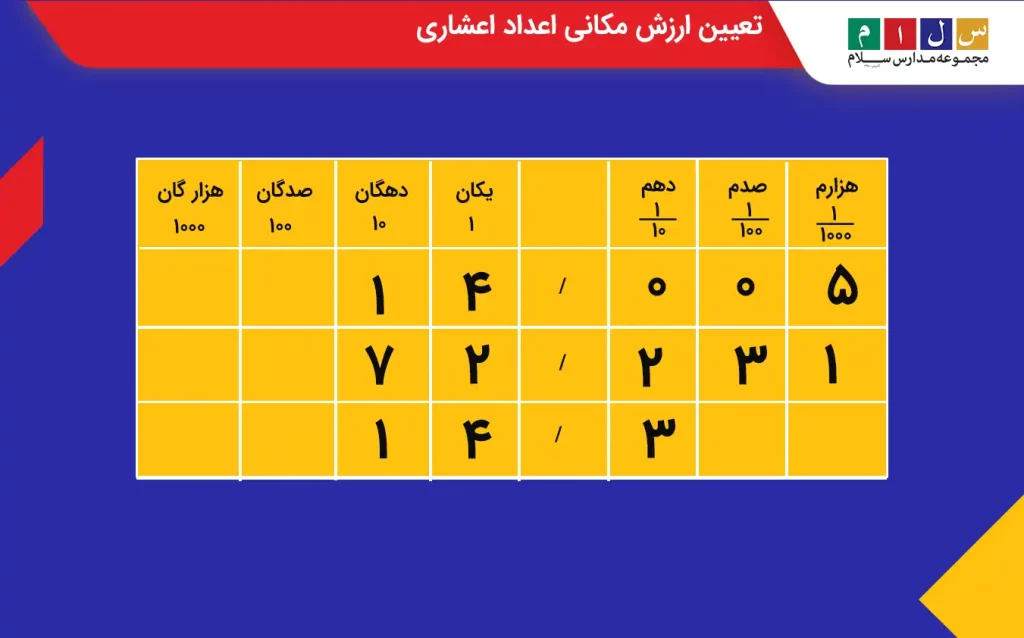
این جدول سه عدد اعشاری را نشان میدهد که بهشکل زیر نوشته و خوانده میشوند:
- ۱۴/۰۰۵ (چهارده و پنجهزارم)
- ۱۷۲/۲۳۱ (صد و هفتاد و دو و دویست و سی و یک هزارم)
- ۱۴/۳ (چهارده و سهدهم)
برای آشنایی با اعداد اول و ویژگیهای آنها، اینجا را بخوانید و اطلاعات کامل بدست آورید
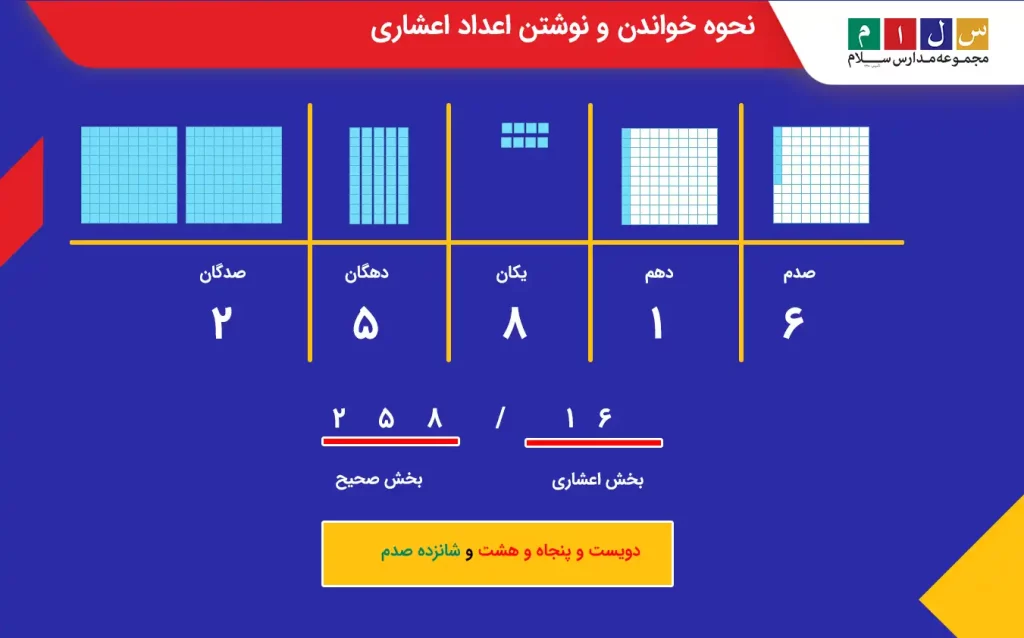
مثال ۱: عدد ۲۵۸/۱۶ را در جدول ارزش مکانی نشان دهید.
جواب: در تصویر زیر علاوهبر ارزش مکانی، نحوه نوشتن و خواندن عدد موردنظر نشان داده شده است.
مثال ۲: اعداد اعشاری زیر را از کوچک به بزرگ مرتب کنید.
۱/۵ و ۰/۰۰۴ و ۱۰/۰۷ و ۰/۱ و ۰/۱۲
جواب: برای نوشتن اعداد اعشاری از کوچک به بزرگ باید به بزرگ و کوچکی اعداد و ارزش مکانی آنها توجه کنیم. یعنی باید ارزشهای مکانی اعداد را از سمت چپ به سمت راست بررسی کنیم. ابتدا سراغ عددی میرویم که قسمت صحیح آن از بقیه بزرگتر باشد. تنها دو عدد ۱/۵ و ۱۰/۰۷ قسمت صحیحشان غیرصفر است و از بین این دو عدد هم عدد صحیح ۱۰/۰۷ که برابر با ۱۰ است، بزرگتر است.
سه عدد ۰/۰۰۴ و ۰/۱ و ۰/۱۲چون بخش صحیحشان صفر است، ارزش مکانی قسمت اعشارشان را مقایسه میکنیم. عدد ۰/۱۲ (دوازدهصدم) یعنی ۱۲ قسمت از ۱۰۰ قسمت و عدد ۰/۱ (یکدهم) نیز یعنی یک قسمت از ۱۰ قسمت. برای مقایسه راحتتر این دو عدد، عدد ۰/۱ را بهصورت ۰/۱۰ (۱۰ قسمت از ۱۰۰ قسمت) مینویسیم. توجه داشته باشید که گذاشتن صفر جلوی قسمت اعشار تأثیری در مقدار آن عدد ندارد. ازآنجا که ۱۲ تا از ۱۰۰ تا بزرگتر از ۱۰ تا از ۱۰۰ تا است عدد ۰/۱۲ از ۰/۱ بزرگتر خواهد بود.
بنابراین، ترتیب اعداد بالا از کوچک به بزرگ بهشکل زیر خواهد بود (هرچه بهسمت راست میرویم اعداد بزرگتر میشوند):
۱۰/۰۷ و ۱/۵ و ۰/۱۲ و ۰/۱ و ۰/۰۰۴
پیشنهاد مطالعه: آموزش گسترده نویسی اعداد صحیح و اعشاری با مثال
تبدیل اعداد اعشاری به کسر
برای تبدیل عدد اعشاری به کسر و تبدیل کسر به اعشار باید به نحوه خواندن عدد اعشاری و کسر توجه کنیم. مثلاً وقتی میگوییم ۰/۳۵ (سیوپنج صدم) یعنی ۳۵ قسمت از ۱۰۰ قسمت. بنابراین شکل کسری این عدد اعشاری بهصورت ۳۵صدم نوشته میشود. درادامه چند عدد اعشاری را به کسر تبدیل میکنیم تا بهتر متوجه شوید.

همانطور که میبینید، وقتی یک عدد اعشاری را به کسر تبدیل میکنیم، مخرج کسر ضریبی از ۱۰ میشود مانند ۱۰، ۱۰۰، ۱۰۰۰ و غیره.
بهدلیل کاربرد اعداد اعشاری در زندگی روزمره، در ادامه شما را با چهار عمل اصلی در انواع اعداد اعشاری آشنا میکنیم.
جمع اعداد اعشاری
جمع اعداد اعشاری مانند جمع معمولی اعداد کامل است، اما هنگام انجام آن باید به نکات زیر توجه کنید:
- اعداد اعشاری را باید بهگونهای زیر هم قرار دهید که اعداد دارای ارزش مکانی یکسان و همچنین ممیزها زیر هم قرار بگیرند.
- اگر تعداد رقمهای سمت راست ممیز اعداد اعشاری با هم برابر نیستند، با اضافه کردن صفر در سمت راست ممیز، تعداد رقمهای قسمت اعشار اعداد را شبیه به هم کنید. اضافه کردن صفر در این مرحله روی مقدار عددی تأثیری ندارد.
- در مرحله آخر، از سمت راست عمل جمع کردن را شروع کنید و اعداد زیر هم را با یکدیگر جمع کنید. هرجا به ممیز اعداد اعشاری رسیدید، یک ممیز در همانجا در قسمت پاسخ قرار دهید.
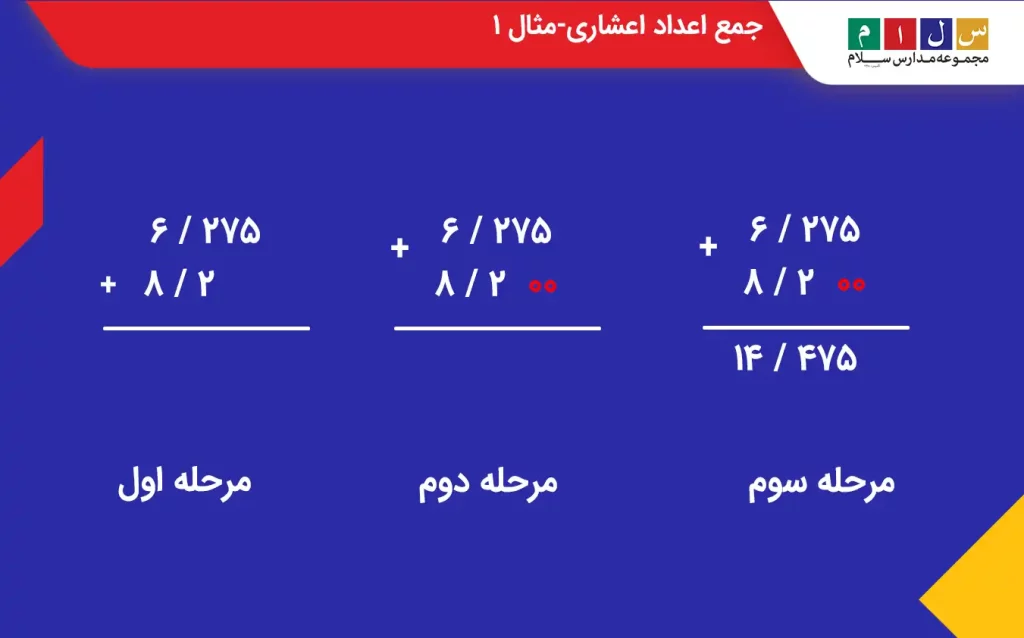
مثال ۱: مجموع اعداد ۶/۲۷۵ و ۸/۲ را بهدست آورید.
جواب: با توجه به مراحل گفتهشده در بالا جمع این دو عدد را بهشکل زیر بهدست میآوریم:
مثال ۲: اعداد ۳ و ۷/۴۹ را با هم جمع کنید.
جواب: عدد ۳ یک عدد کامل است. برای اینکه آن را با یک عدد اعشاری جمع کنیم، باید با قرار دادن ممیز و صفر جلوی آن تعداد رقمهایش را برابر با تعداد رقمهای عدد اعشاری کنیم.

پیشنهاد مطالعه: انجام راحت محاسبات با جمع و تفریق فرایندی
تفریق اعداد اعشاری
مراحل تفریق اعداد اعشاری بهشکل زیر است:
- عدد اعشاری کوچکتر را زیر عدد اعشاری بزرگتر بهگونهای قرار دهید که ممیزها و اعداد دارای ارزش مکانی یکسان زیر هم قرار بگیرند.
- اگر تعداد رقمهای سمت راست ممیز اعداد اعشاری با هم مساوی نیستند، با اضافه کردن صفر در سمت راست اعشار، تعداد رقمهای قسمت اعشار اعداد را شبیه به هم کنید.
- از سمت راست به چپ عمل تفریق را انجام دهید و اعداد زیر یکدیگر را از هم کم کنید. هرجا به ممیز اعداد اعشاری رسیدید، یک ممیز در همانجا در قسمت جواب قرار دهید.
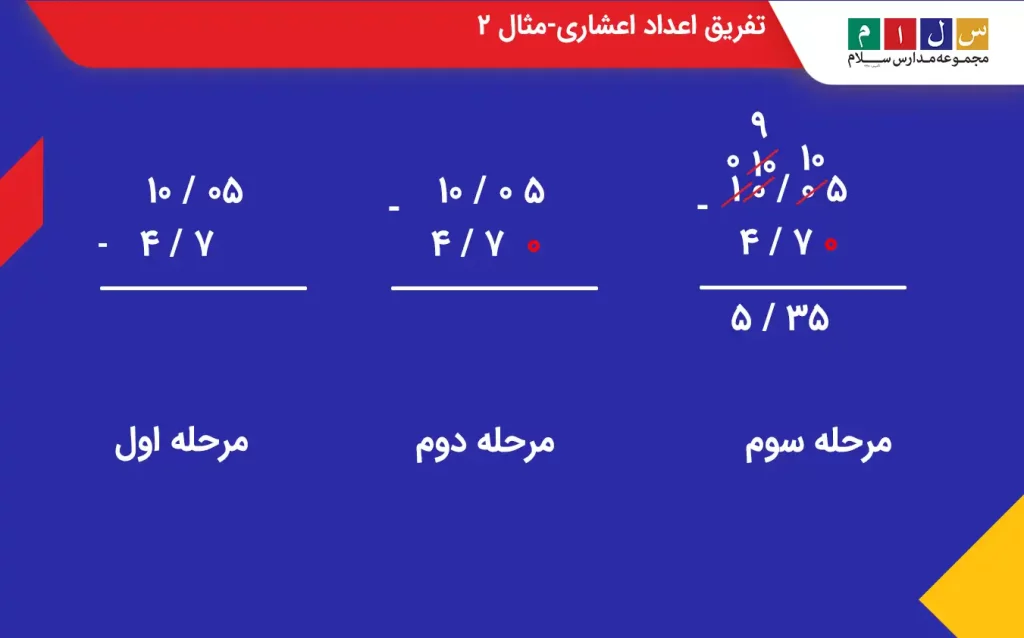
مثال: حاصل تفریق مجموعه اعداد زیر را تعیین کنید.
الف) ۹/۷۶ و ۵/۳
ب) ۱۰/۰۵ و ۴/۷
جواب: عمل تفریق را طبق مراحلی که بیان کردیم انجام میدهیم.
الف)

ب)
ضرب اعداد اعشاری
ضرب اعداد اعشاری مشابه ضرب اعداد کامل انجام میشود، با این تفاوت که محل قرارگیری ممیز در پاسخ حاصلضرب تغییر میکند. بهطور کلی، ضرب اعداد اعشاری را باید طبق مراحل زیر انجام دهید:
- اعداد را بدون در نظر گرفتن ممیز در هم ضرب کنید.
- پس از ضرب، تعداد رقمهای اعشار اعدادی که ضرب کردهاید را با هم جمع کنید و بههمان اندازه از سمت راست پاسخ رقم اعشار جدا کنید.
مثال ۱: حاصلضرب اعداد ۴ و ۷/۹ را محاسبه کنید.
جواب: ابتدا بدون در نظر گرفتن ممیز دو عدد را در هم ضرب میکنیم:
۴ × ۷/۹ = ۳/۱۶
حالا به تعداد رقمهای اعشار عاملهای ضرب از سمت راست حاصلضرب، رقم اعشار جدا میکنیم. در اینجا فقط عدد ۷/۹ رقم اعشار دارد که تعداد آن یک است. بنابراین، از سمت راست ۳۱۶ بهاندازه یک رقم اعشار جدا میکنیم. در نهایت، حاصلضرب این دو عدد بهصورت زیر خواهد بود:
۳۱/۶ = ۷/۹ × ۴
مثال ۲: حاصلضرب اعداد ۰/۲۷ و ۰/۰۱۵ را بهدست آورید.
جواب: برای بهدست آوردن حاصلضرب، ابتدا باید بدون توجه به ممیز اعداد را ضرب کنیم. اگر ممیز اعداد ۰/۲۷ و ۰/۰۱۵ را در نظر نگیریم، این دو عدد بهشکل ۲۷ و ۱۵ خواهند بود. توجه داشته باشید که بدون ممیز، صفر قبل از ۱۵ بیمعنی است و تأثیری در مقدار آن ندارد. حاصلضرب این دو عدد بدون ممیز بهصورت زیر است:
۲۷ × ۱۵ = ۴۰۵
تعداد رقمهای اعشار ۰/۲۷ دو تا و تعداد رقمهای اعشار ۰/۰۱۵ سه تا است؛ یعنی درمجموع پنج رقم اعشار داریم. بنابراین، باید از سمت راست حاصلضرب بهاندازه پنج رقم اعشار جدا کنیم. حاصلضرب یعنی عدد ۴۰۵ سه رقم است و ما باید پنج رقم اعشار جدا کنیم، بنابراین بهجای هر تعداد رقمی که کم داریم صفر قرار میدهیم.
۰/۲۷ × ۰/۰۱۵=۰/۰۰۴۰۵
نکته: اگر اعداد ضریب ۱۰ مانند ۱۰، ۱۰۰، ۱۰۰۰ و غیره در یک عدد اعشاری ضرب شوند، ممیز عدد اعشاری بهاندازه تعداد صفرهای این اعداد جلو برده میشود.
برای مثال، اگر عدد ۱۰۰۰ را در ۵/۶ ضرب کنیم، باید ممیز را بهاندازه صفرهای ۱۰۰۰ یعنی سه رقم اعشار جلو ببریم.

بهجای هر تعداد رقمی که کم داریم صفر قرار میدهیم.
تقسیم اعداد اعشاری
برای تقسیم اعداد اعشاری بر یک عدد صحیح یا یک عدد اعشاری دیگر از دو روش میتوانیم این کار را انجام دهیم: روش مستقیم و روش تبدیل به کسر.
در روش مستقیم، تقریباً مانند تقسیم معمولی عمل تقسیم را انجام میدهیم و هرجا که به ممیز مقسوم رسیدیم در خارجقسمت ممیز میگذاریم. برای اینکه بهتر متوجه شوید یک مثال حل میکنیم.
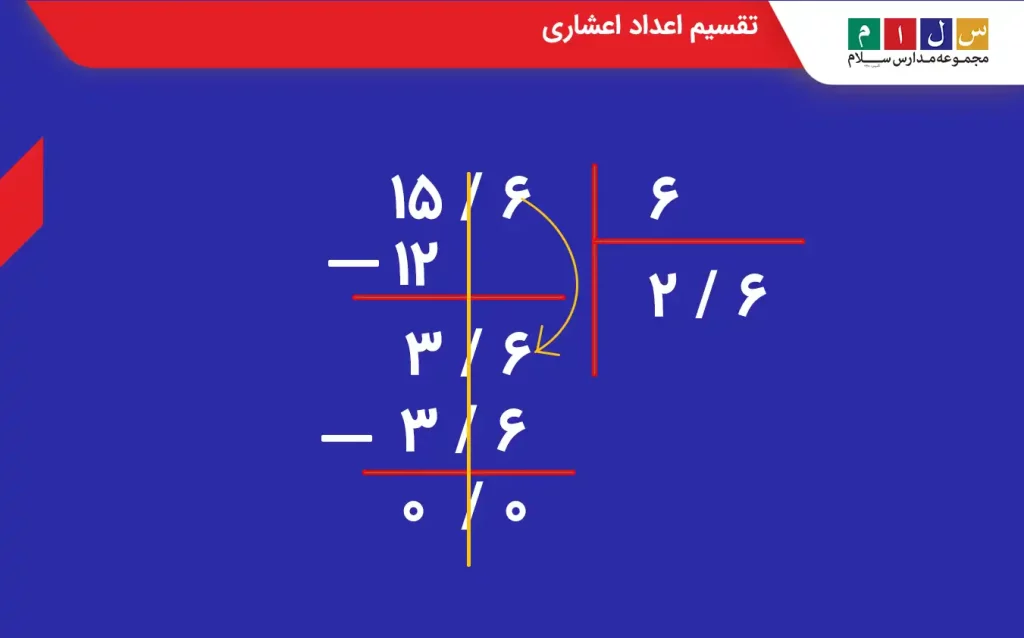
مثال: اگر بخواهیم ۱۵/۶ را بر ۶ تقسیم کنیم، خواهیم داشت:
روش تبدیل به کسر، روش سادهتری برای تقسیم اعداد اعشاری است. در این روش، تقسیم را بهصورت کسر مینویسیم و صورت و مخرج را در عددی ضرب میکنیم که بخش اعشار را از بین ببرد. به مثال زیر توجه کنید:
میخواهیم عدد ۷/۲ را بر ۶ تقسیم کنیم. اگر هر دو عدد (صورت و مخرج) را در ۱۰ ضرب کنیم، ممیز عدد ۷/۲ یک رقم به جلو میرود و بخش اعشاری نخواهیم داشت.
ضرب مقسوم و مقسومعلیه (صورت و مخرج) در یک عدد تأثیری در مقدار خارجقسمت ندارد. بنابراین، حاصل تقسیم ۷/۲ بر ۶ نیز برابر با ۱/۲ خواهد بود.
توجه داشته باشید که مقسوم و مقسومعلیه (صورت و مخرج) در هر عددی ضرب شوند، خارجقسمت تغییر نمیکند، اما باقیمانده تغییر کرده و در آن عدد ضرب میشود.
نکته: اگر یک عدد اعشاری بر ضریبی از ۱۰ مانند ۱۰، ۱۰۰، ۱۰۰۰ و غیره تقسیم شود، ممیز عدد اعشاری بهاندازه تعداد صفرهای این اعداد بهسمت چپ برده میشود.
بهعنوان مثال، اگر عدد ۴۵/۶ را بر ۱۰۰۰ تقسیم کنیم، باید به تعداد صفرهای آن یعنی سه رقم اعشار بهسمت چپ برویم.

بهجای هر تعداد رقمی که کم داریم صفر میگذاریم. حالا که با اعداد اعشاری و انواع عملیات ریاضی در آنها آشنا شدید، پیشنهاد میکنیم نگاهی هم به مقاله تبدیل کسر به عدد مخلوط بیندازید. در ادامه برای تثبیت بهتر مطالب، چند نمونه سؤال از پایههای مختلف حل میکنیم.
نمونه سؤل اعداد اعشاری کلاس چهارم
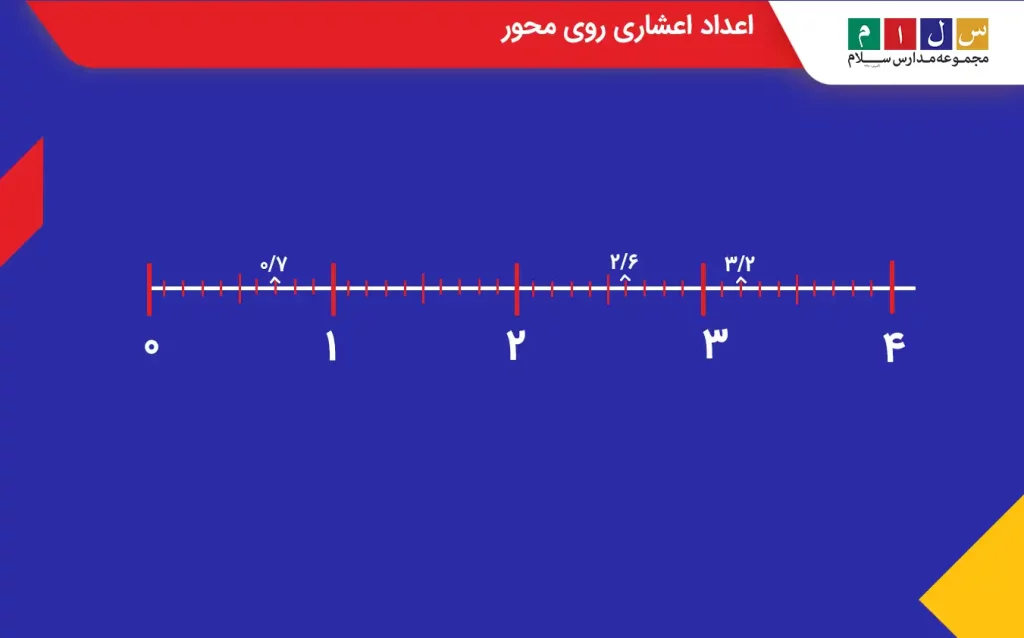
اعداد اعشاری ۳/۲، ۲/۶ و ۰/۷ را روی محور نشان دهید.
جواب: برای نشان دادن اعداد اعشاری روی محور ابتدا باید به قسمت اعشار آن توجه کنیم. در اینجا چون هر سه عدد اعشاری ارزش مکانی دهم دارند باید واحدهای محور را به ده قسمت مساوی تقسیم کنیم. بنابراین، خواهیم داشت:
نمونه سؤل اعداد اعشاری کلاس پنجم
حاصلضرب دو عدد ۰/۹ و ۲۳/۵ را بهدست آورید.
جواب: ابتدا دو عدد را بدون توجه به ممیز در هم ضرب میکنیم:
۹ × ۲۳۵ = ۲۱۱۵
عدد ۰/۹ یک رقم اعشار و ۲۳/۵ هم یک رقم اعشار دارد. بنابراین، درمجموع دو رقم اعشار از سمت راست حاصلضرب جدا میکنیم:
۰/۹ × ۲۳/۵ = ۲۱/۱۵
نمونه سؤل اعداد اعشاری کلاس ششم
عدد ۴/۳۲۵ را بر ۲/۲۵ تقسیم کنید.
جواب: حاصل تقسیم را با استفاده از روش تبدیل بهدست میآوریم.
پیشنهاد مطالعه: میانگین چیست؟
سخن پایانی
اعداد اعشاری اعدادی هستند که از دو بخش صحیح و اعشاری تشکیل شدهاند. این دو بخش با یک ممیز از هم جدا میشوند. درواقع، اعداد اعشاری نشاندهنده اعدادی هستند که بین دو عدد صحیح یا کامل قرار میگیرند. در اعداد اعشاری هرچه به سمت راست پیش میرویم، ارزش مکانی اعداد کمتر میشود و برعکس هرچه بهسمت چپ پیش میرویم، ارزش مکانی اعداد افزایش میباید. چهار عمل ریاضی یعنی جمع، تفریق، ضرب و تقسیم را میتوان برای اعداد اعشاری نیز انجام داد. در این مقاله شیوه انجام آنها را همراه با مثال بهطور مفصل آموزش دادیم.
سؤالات متداول
- اعداد اعشاری چیست؟
اعدادی هستند که از دو بخش صحیح و اعشار ساخته شدهاند. این اعداد بین دو عدد صحیح قرار دارند. - ارزش مکانی اعداد اعشاری چگونه است؟
در اعداد اعشاری هرچه به سمت راست میرویم، ارزش مکانی اعداد کمتر و برعکس هرچه بهسمت چپ میرویم، ارزش مکانی اعداد بیشتر میشود. - آیا اعداد اعشاری را میتوان به کسر تبدیل کرد؟
بله، برای تبدیل اعداد اعشاری به کسر کافیست به نحوه خواندن این اعداد توجه کنیم. این اعداد وقتی به کسر تبدیل میشوند، مخرجشان ضریبی از ۱۰ است مانند ۱۰، ۱۰۰، ۱۰۰۰ و غیره. - اعداد اعشاری را چگونه جمع کنیم؟
برای جمع اعداد اعشاری کافیست ممیز و اعدادی که ارزش مکانی یکسانی دارند را زیر هم قرار دهید و بهازای ارقامی که کم دارید صفر قرار دهید. - تفریق اعداد اعشاری چگونه است؟
برای تفریق اعداد اعشاری هم مشابه جمع آنها عمل کرده و عدد کوچکتر را از عدد بزرگتر کم میکنیم. - حاصلضرب اعداد اعشاری را چگونه بهدست آوریم؟
ابتدا دو عدد را بدون در نظر گرفتن ممیز در هم ضرب میکنیم و سپس، بهاندازه مجموع تعداد رقمهای اعشار عاملهای ضرب، از سمت راست حاصلضرب رقم اعشار جدا میکنیم. - اعداد اعشاری را چگونه بر هم تقسیم کنیم؟
برای تقسیم اعداد اعشاری بر یکدیگر راحتترین روش، روش تبدیل تقسیم به کسر است. بهاین صورت که مقسوم و مقسومعلیه (صورت و مخرج) را در ضرایب ۱۰ ضرب میکنیم تا بخش اعشار آنها از بین برود.









