کسینوس چیست ؟ | تعریف + نحوه محاسبه کسینوس زاویه

تابع کسینوس یک تابع مثلثاتی برای بیان ارتباط بین زاویه و طول است. این تابع به‌‌طور گسترده در هندسه، فیزیک و مهندسی مورد استفاده قرار می‌‌گیرد و ازاین‌‌جهت، ابزاری ضروری برای حل مسائل دنیای واقعی محسوب می‌‌شود.

در این آموزش از مجموعه آموزش‌‌های ریاضی به شما خواهیم گفت که کسینوس چیست و چگونه محاسبه می‌‌شود. همچنین، فرمول کسینوس را معرفی کرده و مقدار آن برای زوایای پرکاربرد را بیان خواهیم کرد. چند مثال نیز حل می‌‌کنیم تا با تابع کسینوس بیشتر آشنا شوید.

فرمول کسینوس چیست ؟

تابع «کسینوس» (Cosine) که به‌‌اختصار آن را با Cos نشان می‌‌دهند، یک تابع مثلثاتی است که طول و زاویه را به هم ربط می‌‌دهد.

این تابع را می‌‌توان به دو صورت مورد بحث قرار داد:

• با استفاده از مثلث قائم الزاویه
• با استفاده از دایره واحد

در ادامه، تابع کسینوس را با کمک این دو تعریف می‌‌کنیم.

پیشنهاد مطالعه: زاویه چیست؟

تعریف کسینوس با مثلث قائم الزاویه

برای یک مثلث قائم‌‌الزاویه که یکی از زوایای حاده آن θ است، مقدار کسینوس زاویه (θ) به‌‌صورت نسبت ضلع مجاور آن زاویه به وتر مثلث تعریف می‌‌شود:

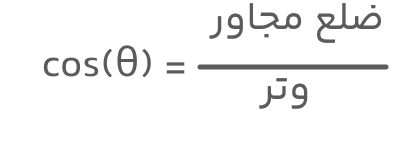
به‌‌طور کلی، در توابع مثلثاتی اضلاع مثلث قائم‌‌الزاویه به‌‌صورت زیر تعریف می‌‌شوند:

• ضلع مجاور: ضلعی که در کنار زاویه θ قرار دارد و وتر نیست.
• ضلع مقابل: ضلعی که مقابل زاویه θ قرار دارد.
• وتر: طولانی‌‌ترین ضلع مثلث که روبه‌‌روی زاویه قائمه قرار دارد.

مثال: مقدار کسینوس زاویه θ را در مثلث زیر به‌‌دست آورید.

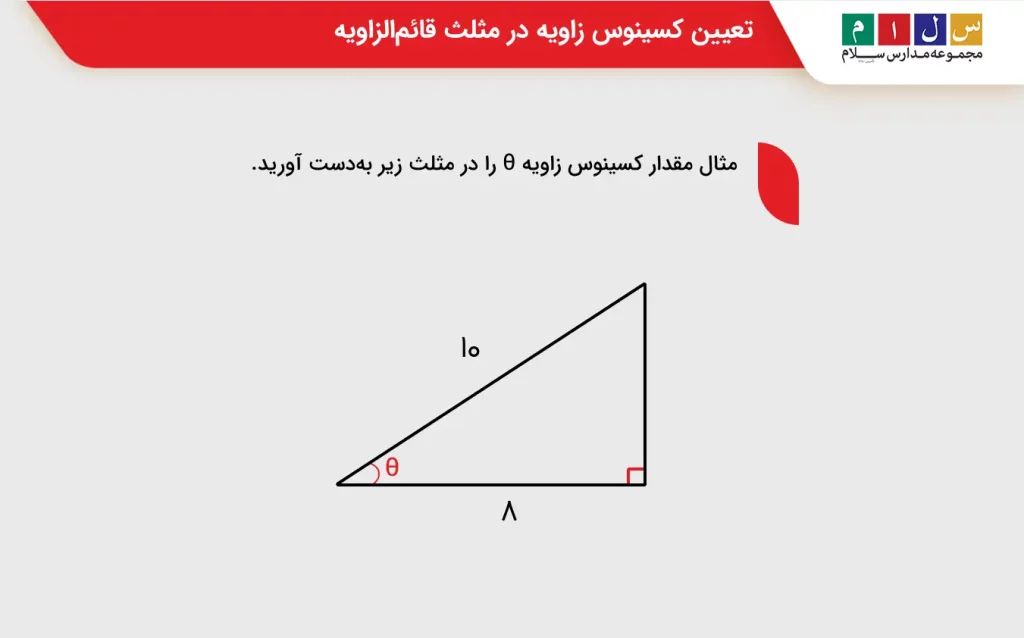
با توجه به تعریف بالا، می‌‌دانیم که کسینوس از تقسیم طول ضلع مجاور زاویه به طول وتر به‌‌دست می‌‌آید. کافی‌‌ست اندازه اضلاع را در این نسبت جای‌‌گذاری کنیم تا مقدار کسینوس تعیین شود. خواهیم داشت:

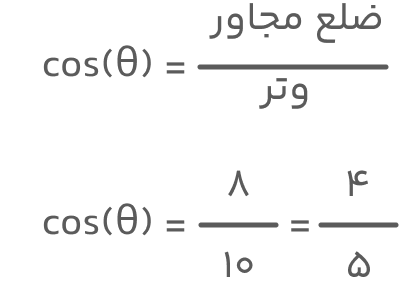
کاربرد کسینوس به همین مثال ختم نمی‌‌شود؛ در حل مسائل دنیای واقعی نیز این تابع بسیار مورد استفاده قرار می‌‌گیرد. به مثالی که در ادامه آورده‌‌ایم توجه کنید تا با نمونه‌‌ای از کاربرد تابع کسینوس آشنا شوید.

مثال: شخصی یک هواپیمای در حال پرواز را بر فراز خود می‌‌بیند. زمانی که فاصله مستقیم بین شخص و هواپیما ۱۴ مایل است، این فرد زاویه‌‌ای را که هواپیما با افق می‌‌سازد ۲۵ درجه ثبت می‌‌کند. فاصله افقی بین هواپیما و شخص چقدر است؟

جواب: ابتدا طبق صورت مسئله یک مثلث قائم‌‌الزاویه مانند شکل زیر رسم می‌‌کنیم و اطلاعات داده‌‌شده را می‌‌نویسیم. فاصله افقی شخص و هواپیما را x و فاصله مستقیم هواپیما و شخص را که ۱۴ مایل است وتر مثلث قرار می‌‌دهیم.
حال با استفاده از تعریف کسینوس در بخش کسینوس چیست می‌‌توانیم مقدار مجهول x را به‌‌دست آوریم. دقت کنید که در اینجا زاویه حاده ۲۵ درجه است.

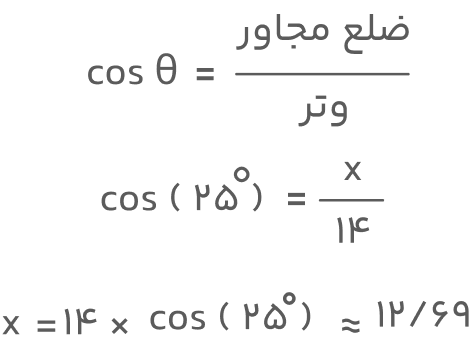
بنابراین، فاصله افقی بین شخص و هواپیما تقریباً ۱۲/۶۹ مایل است.

تعریف کسینوس با دایره واحد

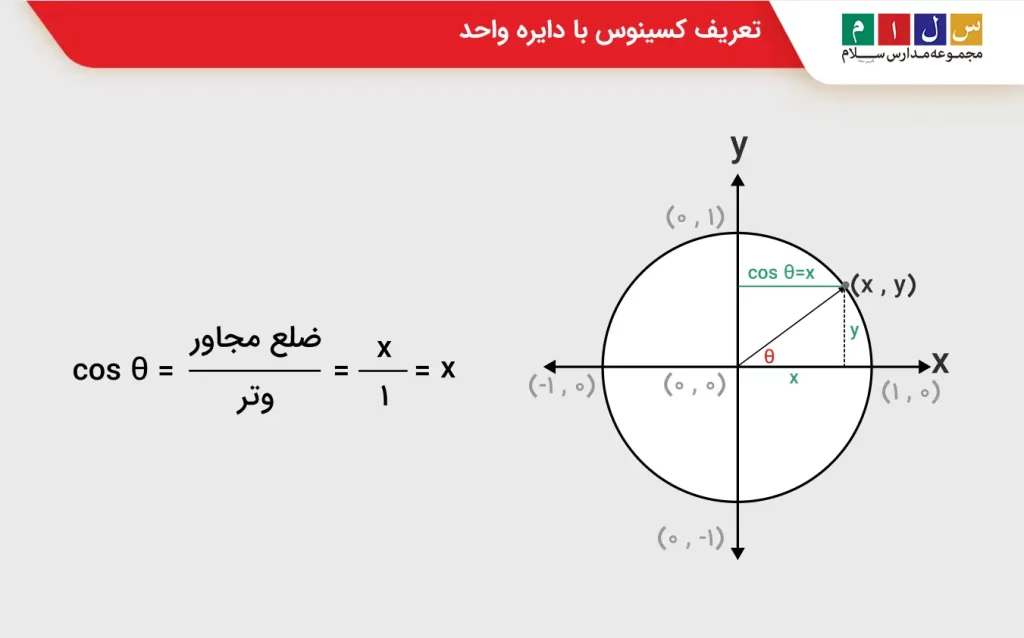
توابع مثلثاتی ازجمله کسینوس را می‌‌توان با استفاده از یک دایره واحد (یا دایره مثلثاتی) نیز تعریف کرد. منظور از دایره واحد دایره‌‌ای به شعاع یک واحد است که مرکز آن در مبدأ مختصات قرار دارد. همان‌‌طور که دیدید، در تعریف کسینوس با استفاده از مثلث قائم‌‌الزاویه تنها می‌‌توان کسینوس زوایای ۰ تا ۹۰ درجه را محاسبه کرد. اما در دایره واحد اینگونه نیست. این دایره به ما این امکان را می‌‌دهد که توابع مثلثاتی را به همه اعداد حقیقی تعمیم دهیم. به شکل زیر نگاه کنید. این شکل دایره واحد را نشان می‌‌دهد.

نقطه‌‌ای مانند (x , y ) را روی محیط دایره در نظر می‌‌گیریم و مانند تصویر زیر، یک مثلث قائم‌‌الزاویه با کمک این نقطه تشکیل می‌‌دهیم. وتر این مثلث همان شعاع دایره واحد یعنی ۱ است. θ نیز زاویه تشکیل‌‌شده بین وتر و محور x هاست. اکنون که می‌‌دانیم کسینوس چیست محاسبه کسینوس زاویه θ برایمان راحت است. مقدار کسینوس به‌‌صورت زیر خواهد بود:

این مقدار نشان می‌‌دهد که مقدار x برای هر نقطه روی محیط دایره واحد برابر با cos است.

زاویه های پرکاربرد در مثلثات

اگرچه ما می‌‌توانیم کسینوس هر زاویه‌‌ای را محاسبه کنیم، اما برخی زاویه‌‌ها هستند که در مثلثات بیشتر به‌‌کار می‌‌روند. در تصویر زیر ۱۶ زاویه پرکاربرد برحسب رادیان و درجه به‌‌همراه مختصات نقاط متناظر آن‌‌ها روی دایره واحد آمده است. توجه داشته باشید که در دایره مثلثاتی زیر جهت مثبت چرخش، خلاف جهت حرکت عقربه‌‌های ساعت است.
نکته: هر π رادیان برابر با ۱۸۰ درجه است.

اگر جهت چرخش در دایره مثلثاتی در جهت منفی یعنی به‌‌صورت ساعتگرد (در جهت عقربه‌‌های ساعت) باشد، آنگاه زاویه منفی خواهد بود. برای مثال، اگر از صفر درجه شروع کنیم و به‌‌اندازه ۴۵ درجه چرخش پادساعتگرد داشته باشیم زاویه را همان ۴۵ درجه نشان می‌‌دهیم، اما اگر در جهت منفی، ۴۵ درجه پیش برویم، آنگاه زاویه منفی بوده و آن را با ۴۵- درجه نشان می‌‌دهیم. بنابراین، زاویه‌‌ای که علامت منفی دارد نشان‌‌دهنده حرکت ساعتگرد یا چرخش در جهت منفی دایره مثلثاتی خواهد بود.

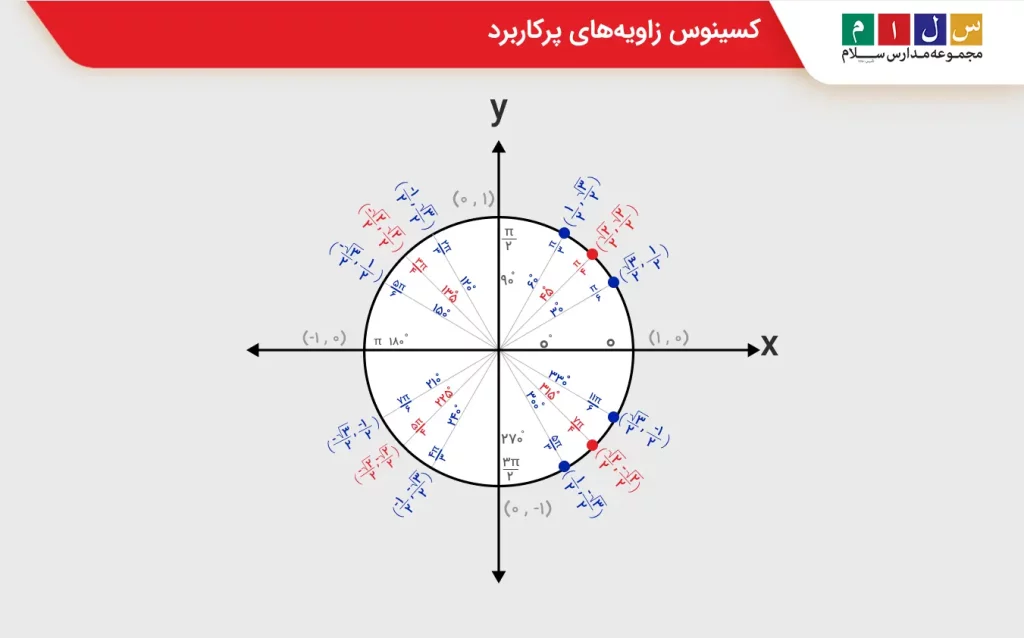
در این تصویر، مقدار x کسینوس زاویه مربوطه و مقدار y سینوس آن زاویه را نشان می‌‌دهد. همان‌‌طور که در شکل دیده می‌‌شود، در زاویه ۹۰ درجه، کسینوس مقدار ۰ و در زاویه ۰ درجه مقدار ۱ را دارد. در ربع اول، هرچه زاویه بزرگ‌‌تر می‌‌شود مقادیر کسینوس کاهش می‌‌یابد. جدول زیر این موضوع را به‌‌خوبی نشان می‌‌دهد.

در ربع اول و چهارم، مقدار کسینوس مثبت و در ربع دوم و سوم منفی است که این امری بدیهی به نظر می‌‌رسد، زیرا همان‌‌طور که قبلاً هم توضیح دادیم در دایره مثلثاتی مقدار x در هر نقطه روی محیط دایره برابر با cos است و چون مقادیر x در ربع اول و چهارم مثبت و در ربع دوم و سوم منفی است مقدار cos نیز به همین صورت خواهد بود. در ادامه برای درک بهتر، مقدار چند زاویه پرکاربرد را به‌‌صورت جداگانه روی شکل نشان داده‌‌ایم.

کسینوس ۶۰

۶۰ درجه معادل رادیان است و در دایره مثلثاتی به‌‌صورت زیر نشان داده می‌‌شود:

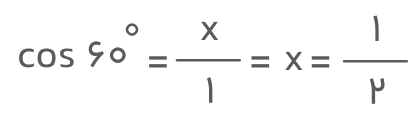
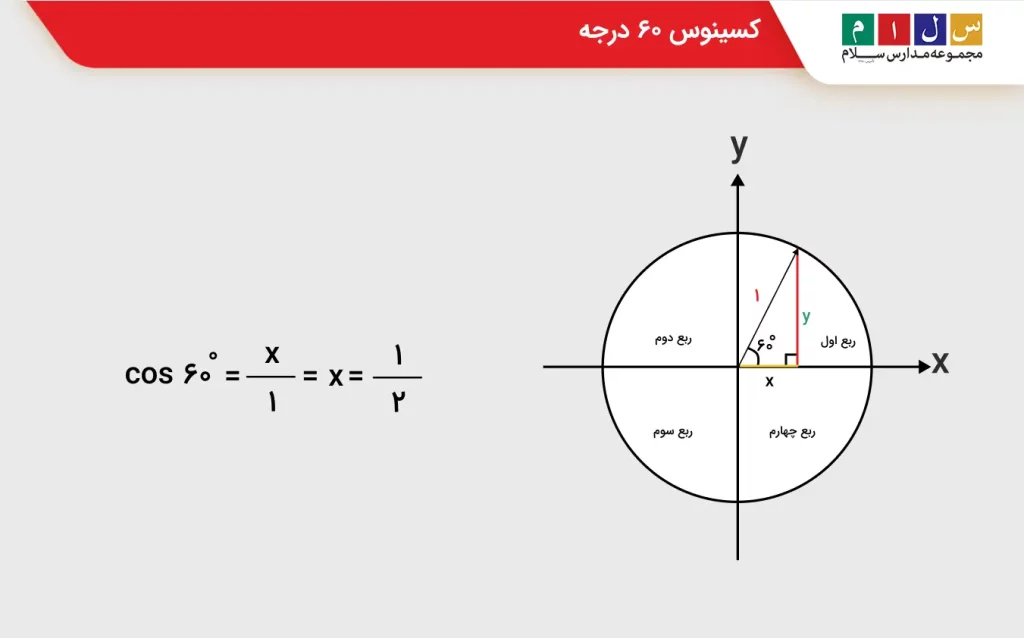
کسینوس ۱۲۰

زاویه ۱۲۰ درجه یا رادیان در ربع دوم دایره مثلثاتی قرار می‌‌گیرد یعنی جایی که مقدار xها منفی است. پس اندازه کسینوس این زاویه برابر با اندازه کسینوس زاویه ۶۰ درجه اما با علامت منفی خواهد بود.

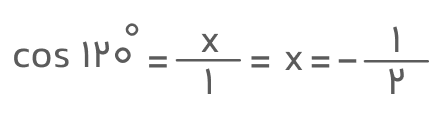
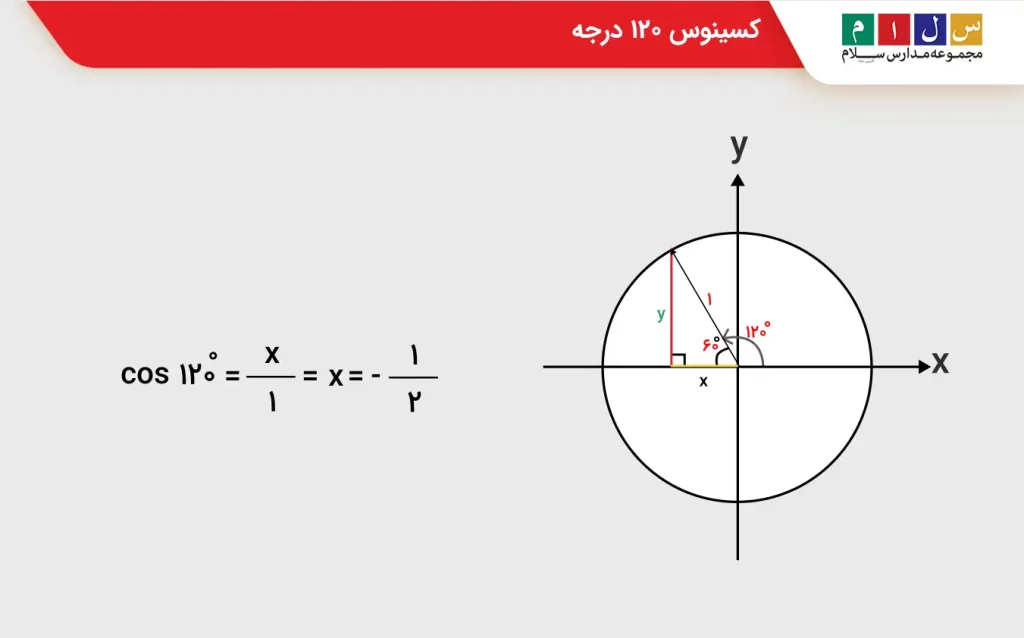
کسینوس ۱۸۰

زاویه ۱۸۰ درجه یا π رادیان در راستای محور xها قرار دارد. اگر از صفر درجه شروع کرده و در خلاف جهت عقربه‌‌های ساعت به‌‌اندازه ۱۸۰ درجه بچرخیم، می‌‌بینیم که این زاویه دقیقاً بر محور xها و مقادیر منفی x منطبق می‌‌شود. پس زاویه ۱۸۰ درجه و ۰ درجه قرینه یکدیگر هستند.

cos ۱۸۰° = -۱

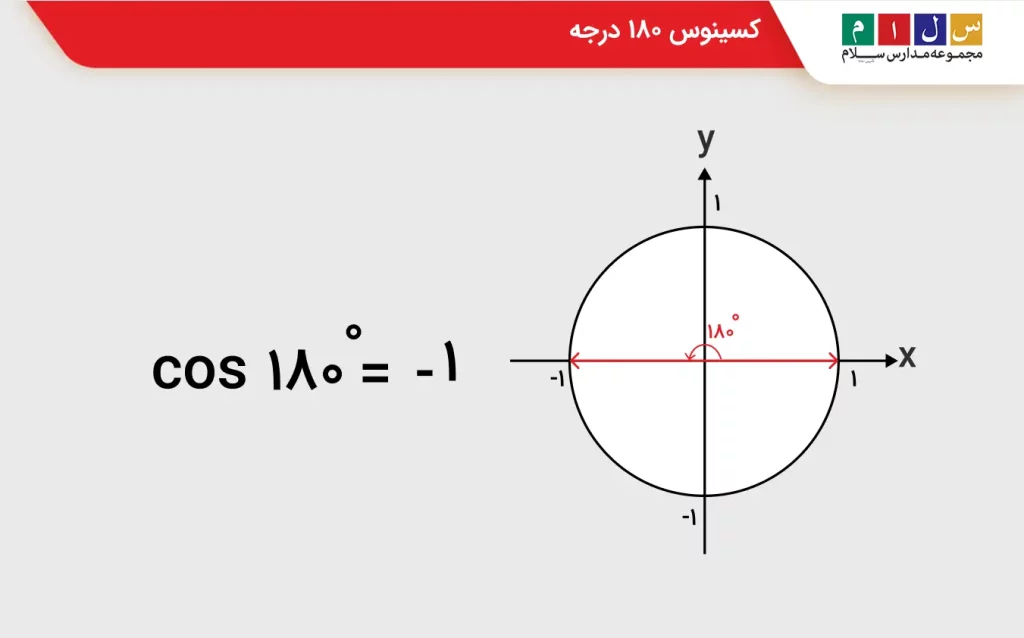
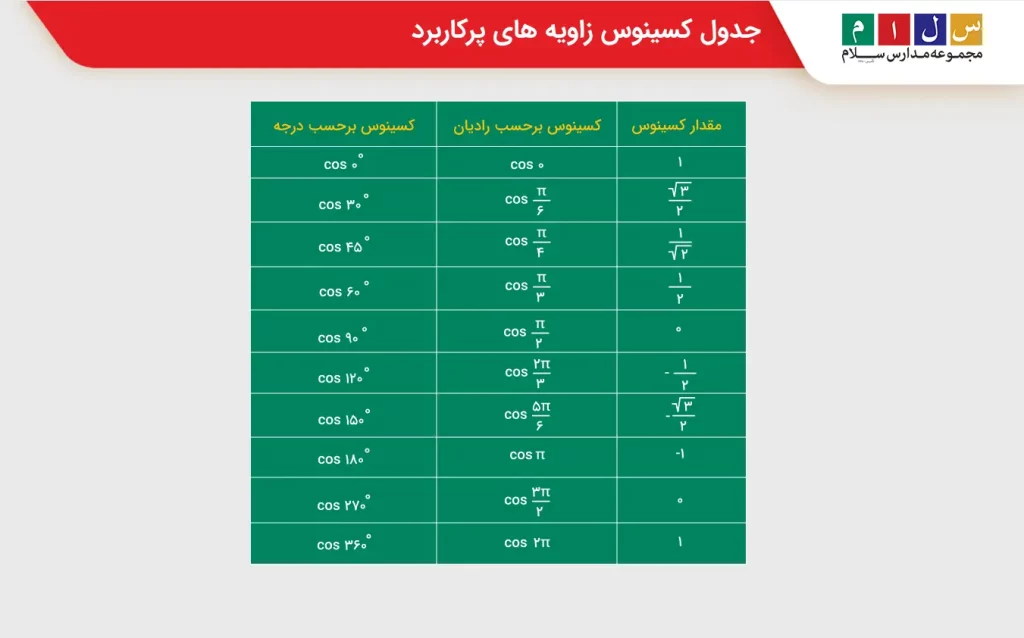
جدول کسینوس زاویه های پرکاربرد

ما در حل مسائل و برخی از امور روزمره نیاز داریم مقدار کسینوس برخی از زوایای پرکاربرد را به خاطر بسپاریم. به همین منظور و برای دسترسی راحت‌‌تر به این مقادیر، آن‌‌ها را در قالب یک جدول آورده‌‌ایم.

زاویه مرجع در مثلثات چیست؟

زاویه مرجع زاویه‌‌ای حاده (کمتر از ۹۰ درجه) است که برای نمایش یک زاویه با هر اندازه‌‌ای می‌‌توان از آن استفاده کرد. هر زاویه‌‌ای در صفحه مختصات زاویه مرجعی دارد که بین ۰ و ۹۰ درجه است. این زاویه نسبت به محور x همواره کوچک‌‌ترین زاویه‌‌ای است که می‌‌توان از ضلع دوم یک زاویه ایجاد کرد. شکل زیر زاویه θ و زاویه مرجع آن ‘ θ را نشان می‌‌دهد.

ازآنجا که ‘ θ زاویه مرجع است، cos θ و’cos θ هر دو مقدار یکسانی دارند. برای مثال، زاویه ۳۰ درجه زاویه مرجع ۱۵۰ درجه است و اگر به دایره مثلثاتی مراجعه کنیم می‌‌توانیم ببینیم که کسینوس‌‌های هر دوی آن‌‌ها بزرگی یکسانی دارند، هرچند که علامت‌‌های آن‌‌ها متفاوت است.

بنابراین، تمام زوایای متناظر دیگر نیز مقادیری با همان بزرگی خواهند داشت و ما فقط باید به علامت آن‌‌ها براساس ربع دایره‌‌ای که ضلع دوم زاویه در آن قرار دارد توجه کنیم. به‌‌طور کلی، برای یافتن زاویه مرجع یک زاویه معین مانند θ می‌‌توانیم طبق مراحل زیر عمل کنیم:

۱) اگر زاویه θ از ۳۶۰ درجه یا ۲π بزرگ‌‌تر بود، ابتدا به تعداد دفعات لازم مقدار ۳۶۰ درجه یا ۲π را از آن زاویه کم می‌‌کنیم (حاصل تفریق باید بین ۰ و ۳۶۰ درجه یا ۰ و ۲π باشد). اگر زاویه حاصل بین ۰ و ۹۰ درجه باشد، آنگاه زاویه مرجع خواهد بود.

۲) مشخص می‌‌کنیم که ضلع دوم زاویه در کدام ربع دایره قرار دارد (ضلع اول زاویه در امتداد و در جهت محور xها است).

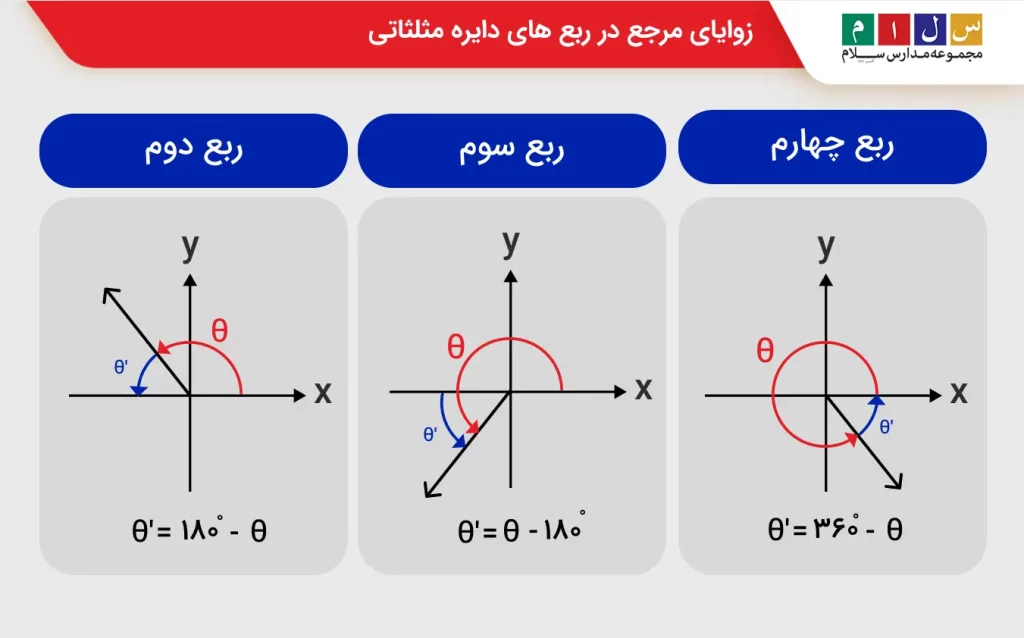
۳) بسته به اینکه ضلع دوم زاویه در کدام ربع قرار می‌‌گیرد، از معادلات جدول زیر برای یافتن زاویه مرجع استفاده می‌‌کنیم. در ربع اول ‘θ = θ است.

برای اینکه نحوه به‌‌دست آوردن زاویه مرجع را بهتر یاد بگیرید، دو مثال در این زمینه حل می‌‌کنیم.
مثال ۱: کسینوس زاویه ۱۲۰ درجه را با کمک زاویه مرجع بیابید.
جواب: زاویه داده‌‌شده یعنی θ بین ۰ و ۳۶۰ درجه است. بنابراین دیگر نیازی نیست که ۳۶۰ درجه را از آن کم کنیم. با توجه به اینکه زاویه ۱۲۰ درجه در ربع دوم دایره واحد قرار می‌‌گیرد، زاویه مرجع آن را به‌‌صورت زیر محاسبه می‌‌کنیم:

θ’ =۱۸۰° – θ

۱۸۰° – ۱۲۰° = ۶۰°

زاویه مرجع ۶۰ درجه است. می‌‌دانیم که ازآنجا که زاویه ۱۲۰ درجه در ربع دوم است و کسینوس در این ربع مقداری منفی دارد، خواهیم داشت:

مثال ۲: کسینوس زاویه ۱۰۵۰ درجه را به‌‌دست آورید.

جواب: زاویه ۱۰۵۰ درجه از ۳۶۰ بزرگ‌‌تر است. پس برای اینکه مقدار آن با کمک زاویه مرجع تعیین شود، ابتدا باید تا جای ممکن مقدار ۳۶۰ درجه را از آن کم کنیم.

۱۰۵۰° – ۳۶۰° = ۶۹۰° – ۳۶۰° = ۳۳۰°

زاویه ۳۳۰ درجه در ربع چهارم که مقدار کسینوس مثبت است واقع شده است. ازاین‌‌رو، زاویه مرجع این زاویه به‌‌صورت زیر محاسبه خواهد شد:

θ’ = ۳۶۰° – θ

۳۶۰° – ۳۳۰° = ۳۰°

با توجه به مقدار کسینوس زاویه مرجع یعنی زاویه ۳۰ درجه، داریم:

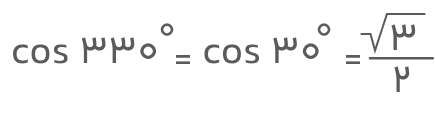
ویژگی های تابع کسینوس چیست ؟

تابع کسینوس دارای ویژگی‌‌های بسیاری است که اگر آن‌‌ها را یاد بگیرید و به ذهن خود بسپارید، درک بسیاری از مباحث ریاضی و هندسی که در آینده با آن‌‌ها آشنا خواهید شد، برایتان راحت‌‌تر خواهد بود. این ویژگی‌‌ها عبارت‌‌اند از:

۱) کسینوس تابعی زوج است. به‌‌طور کلی، تابع f را تابعی زوج می‌‌گویند اگر (f (x)=f (-x باشد. به این معنی که اگر نمودار تابع f را نسبت به محور y بازتاب دهیم، همان نمودار به‌‌دست خواهد آمد. با توجه به زوج بودن تابع کسینوس داریم:

cos (θ) = cos (-θ)

برای مثال:

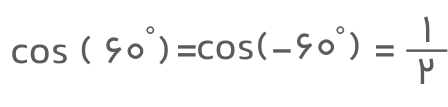
۲) دامنه تابع کسینوس تمام اعداد حقیقی و برد آن است. این یعنی اینکه کسینوس هر زاویه‌‌ای را می‌‌توان به‌‌دست آورد، اما خروجی نهایی این تابع فقط در بازه قرار می‌‌گیرد.

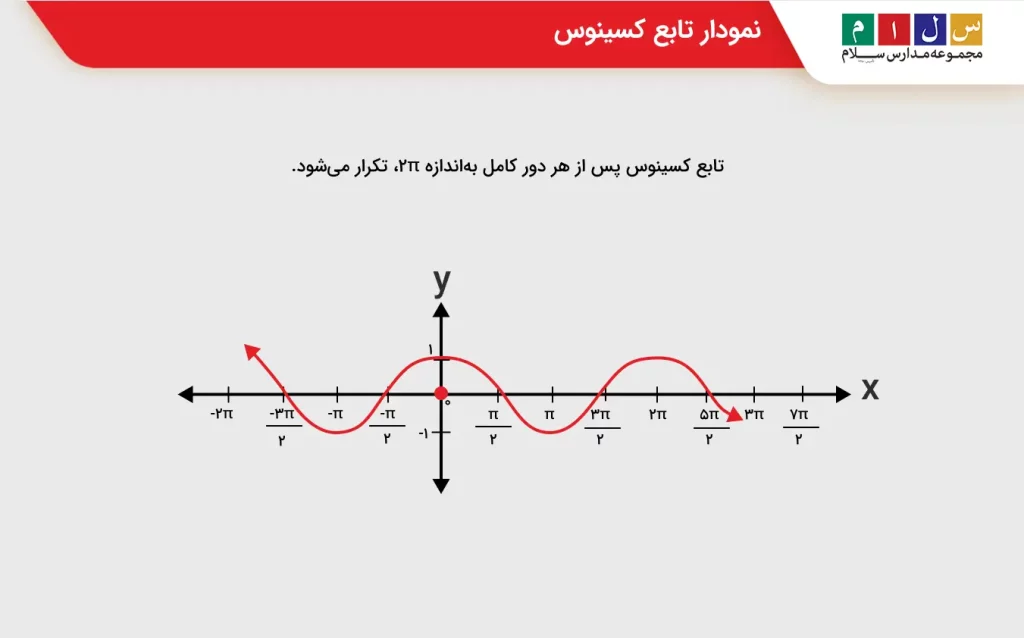
۳) کسینوس تابعی متناوب است. اگر از یک نقطه روی دایره مثلثاتی شروع کرده و در امتداد دایره مسافت ۳۶۰ درجه یا ۲π را طی کنیم، به نقطه شروع باز خواهیم گشت. تابع کسینوس پس از هر دور کامل به‌‌اندازه ۲π، تکرار می‌‌شود. بنابراین، دوره تناوب این تابع ۲π است. نمودار تابع کسینوس در تصویر زیر متناوب بودن آن را به‌‌خوبی نمایش می‌‌دهد.

اگر چندین دور کامل داشته باشیم، این رابطه را می‌‌توان به‌‌صورت زیر نیز نوشت:

در اینجا n عددی صحیح است.

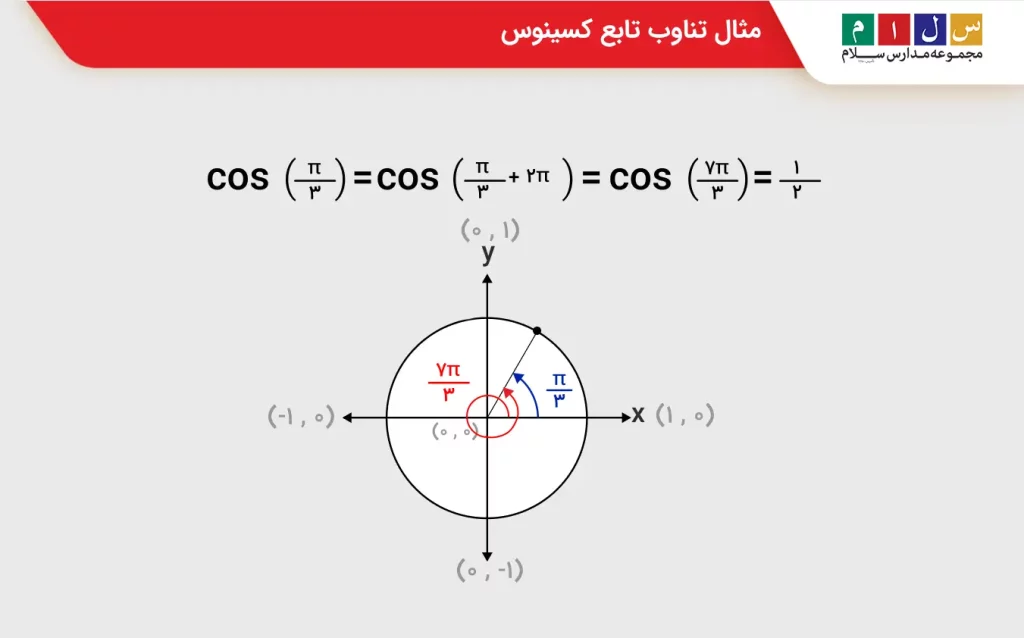
با یک مثال، متناوب بودن تابع کسینوس را روی دایره مثلثاتی بررسی می‌‌کنیم. شکل زیر را در نظر بگیرید. این شکل نشان می‌‌دهد که اگر به مقدار ۲π را اضافه کنیم، مقدار کسینوس هیچ تغییر نخواهد کرد زیرا همان‌‌طور که گفتیم تابع کسینوس پس از هر بار چرخش کامل (۲π رادیان) تکرار می‌‌شود. پس خواهیم داشت:

به دو مثال زیر نگاه کنید. در این مثال‌‌ها با استفاده از خاصیت تناوبی کسینوس، مقدار کسینوس دو زاویه را محاسبه کرده‌‌ایم.

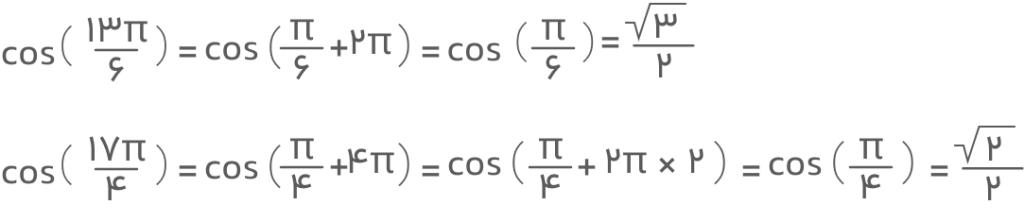
وارون تابع کسینوس

وارون تابع کسینوس را «آرک کسینوس» می‌‌گویند و آن را به‌‌صورت arccosx یا نمایش می‌‌دهند. وارون کسینوس به‌‌شکل زیر تعریف می‌‌شود:

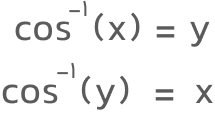
دامنه تابع آرک کسینوس همان برد تابع کسینوس است یعنی تمام اعداد حقیقی در بازه و برد آن نیز شامل تمام اعداد حقیقی در بازه است.

نکته: اگر تابع کسینوس را به مخرج برده و در صورت نیز عدد یک قرار دهیم، تابع جدیدی به‌‌نام «سکانت» (secant) ایجاد خواهد شد که آن را به‌‌صورت زیر نشان می‌‌دهیم:

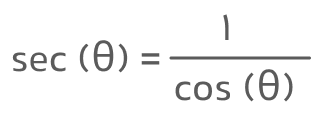
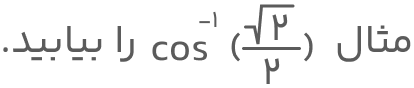
جواب: براساس تعریف تابع وارون کسینوس داریم:

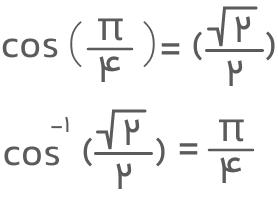
سخن پایانی

در این مقاله یاد گرفتیم که تابع کسینوس چیست و چگونه محاسبه می‌‌شود. تابع کسینوس یکی از توابع مهم مثلثاتی است که در هندسه و ریاضی بسیار کاربرد دارد. معمولاً زمانی که صحبت از مثلثات به میان می‌‌آید، دانش‌‌آموزان از آن به‌‌عنوان مبحثی دشوار و غیرقابل فهم یاد می‌‌کنند، اما همان‌‌طور که در این آموزش خواندید یادگیری این مفهوم ریاضی و هندسی آن‌‌چنان که درباره آن می‌‌گویند، چندان سخت نیست. حل سؤال و تمرین‌‌های پی‌‌درپی می‌‌تواند یادگیری را برایتان آسان‌‌تر و حتی جذاب‌‌تر کند.