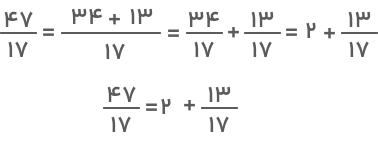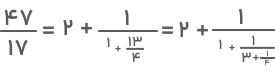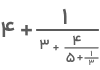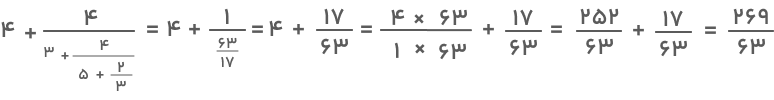فهرست مطالب
Toggleکسرهای مسلسلی روشی برای نمایش اعداد هستند که بهصورت حاصلجمع بخش صحیح آن اعداد و معکوس یک عدد دیگر نوشته میشوند. عدد دوم نیز به همین شکل بهصورت مجموع یک عدد صحیح و وارون یک عدد دیگر نوشته میشود و این فرایند تا جای ممکن ادامه مییابد.
تبدیل کسرهای مسلسلی به عدد گویا و بالعکس ازجمله مباحثی است که برای دانشآموزان دشوار به نظر میآید. به همین خاطر، ما در این مقاله قصد داریم روش حل کسر مسلسلی ششم و نهم را به زبانی ساده و با حل تمرینهای کاربردی آموزش دهیم و یادگیری آن را برایتان آسانتر کنیم.
تبدیل کسر به کسر مسلسلی
روش تبدیل کسر ساده به کسر مسلسلی را با حل یک مثال توضیح میدهیم. کسر را در نظر بگیرید. میخواهیم این کسر را به کسر مسلسلی تبدیل کنیم. از آموزش تبدیل کسر به عدد مخلوط به یاد داریم که کسر بزرگتر از واحد را میتوانیم بهصورت مجموع یک عدد صحیح و یک عدد کسری بنویسیم. برایناساس، کسر موردنظر بهشکل زیر خواهد بود:
اگر عدد دوم یعنی عدد کسری را معکوس کنیم خواهیم داشت:
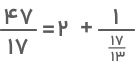
کسر یک کسر بزرگتر از واحد است. پس میتوانیم آن را بهشکل جمع یک عدد صحیح و یک عدد کسری بنویسیم. داریم:
در اینجا میتوانیم کسر را وارون کرده و مانند مراحل قبل آن را بهصورت مجموع عدد صحیح و عدد کسری بیان کنیم:
اگر کسر را معکوس کنیم، خواهیم دید که فقط شامل یک عدد صحیح (یعنی ۴) خواهد بود، درنتیجه نمیتوانیم بیشتر از این تجزیه کسر را ادامه دهیم و در همینجا فرایند تبدیل کسر به کسر مسلسلی پایان مییابد.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
انواع کسر مسلسلی
کسرهای مسلسلی دو نوع هستند:
- کسر مسلسلی متناهی
- کسر مسلسلی نامتناهی
درادامه، هر دو نوع کسر مسلسلی را معرفی میکنیم و روش حل آنها را با مثال توضیح خواهیم داد.
کسرهای مسلسلی متناهی
اگر فرایند تجزیه عدد بهصورت عدد صحیح و عدد کسری که در تبدیل به کسر مسلسلی آن را بیان کردیم، پس از چند مرحله خاتمه یابد، کسر مسلسلی بهدستآمده را کسر مسلسلی متناهی میگوییم. بهطور کلی، نمایش عمومی کسر مسلسلی متناهی یک عدد حقیقی بهصورت زیر است. در نمایش زیرa۰ ، b۱،a۱ و b۲ و… عدد صحیح هستند. (n≥۱)
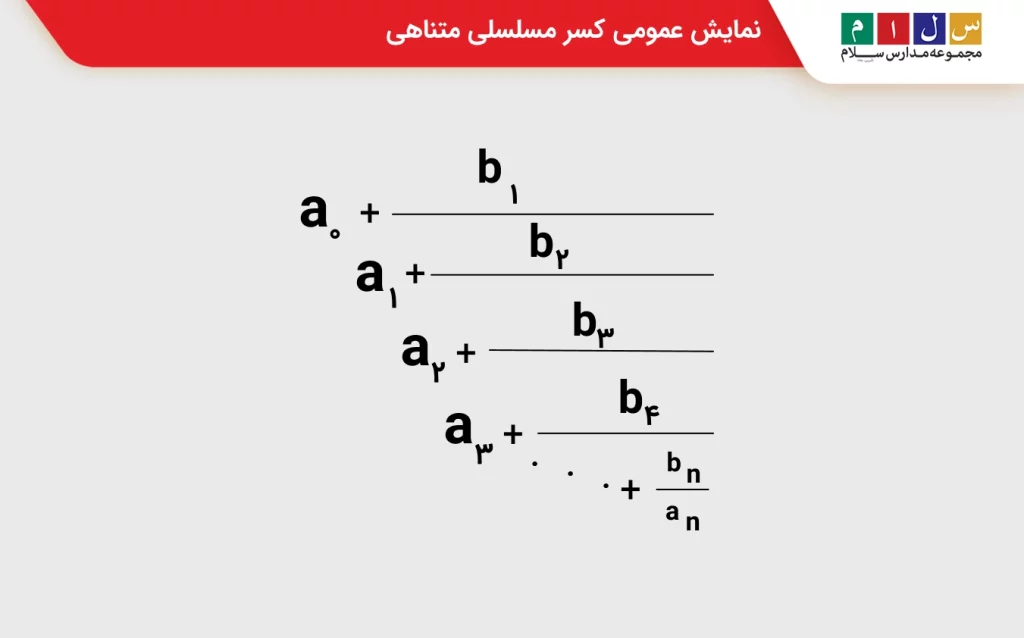
اگر در نمایش بالا، اعداد b1 تا bn برابر با یک باشند، کسر مسلسلی را کسر مسلسلی ساده متناهی مینامیم. در این صورت، کسر مسلسلی بهشکل زیر نمایش داده میشود:

نکته: هر عدد گویا را میتوان به یک کسر مسلسلی ساده متناهی تبدیل کرد.
روش حل کسرهای مسلسلی متناهی
در این بخش، با حل نمونه سؤالی از کسر مسلسلی هشتم، شما را با روش حل کسرهای مسلسلی متناهی آشنا میکنیم. فرض کنید میخواهیم کسر مسلسلی زیر را به یک عدد گویا تبدیل کنیم:
۱) برای حل چنین عبارتهایی از پایینترین کسر شروع میکنیم:
۲) پس از حل این عبارت، سراغ عبارت بعدی میرویم. با روش دور در دور و نزدیک در نزدیک، کسر را به این صورت بازنویسی میکنیم:
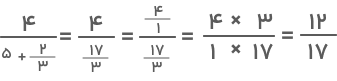
۳) اکنون میتوانیم مخرج کسر جمله دوم را محاسبه کنیم:
۴) در نهایت، پاسخ عبارت موردنظر برابر خواهد بود با
پیشنهاد مطالعه: آموزش تبدیل کسر به اعشار ششم
کسر های مسلسلی نامتناهی
کسرهای مسلسلی نامتناهی به آن دسته از کسرهای مسلسلی گفته میشود که فرایند تجزیه به عدد صحیح و عدد کسری در آنها تا بینهایت ادامه مییابد. نمایش عمومی کسر مسلسلی نامتناهی یک عدد حقیقی را در تصویر زیر نشان دادهایم. در این نمایش، a۰ , b۱ , a۱ , b۱ و … عدد صحیح هستند (n≥۱).
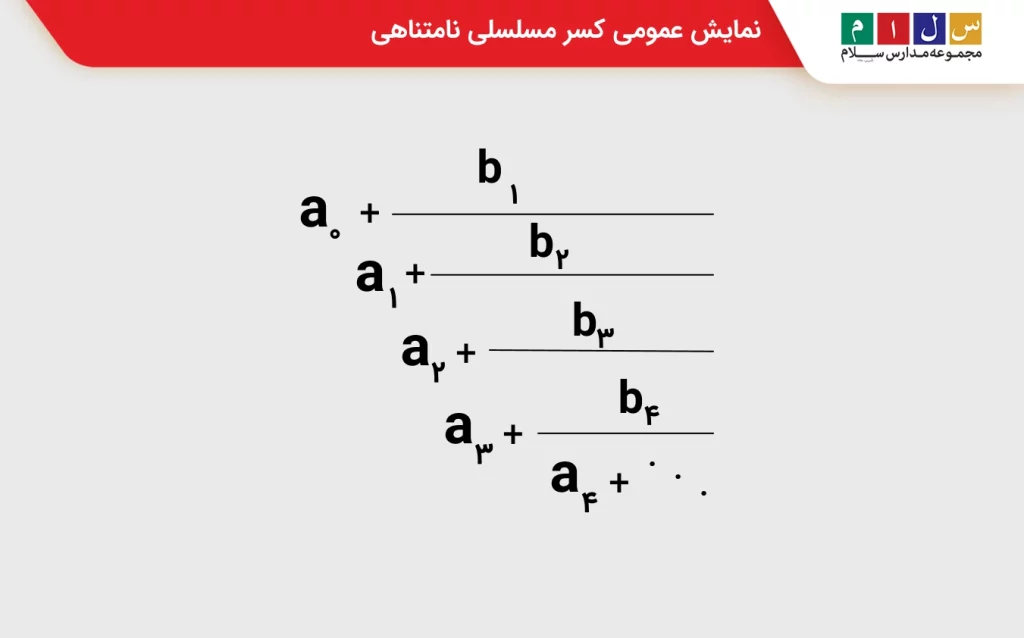
اگر اعداد b۱ تا bn مساوی یک باشند، کسر مسلسلی یک کسر مسلسلی ساده نامتناهی خواهد بود. تصویر زیر، این نوع کسر مسلسلی را نشان میدهد.

روش حل کسر های مسلسلی نامتناهی
حل کسرهای مسلسلی نامتناهی بهدلیل متناهی نبودن شاید اندکی دشوار به نظر برسد، اما ما در اینجا روش حل این نوع کسرها و مراحل آن را به شما آموزش خواهیم داد. به نمونه سوال کسر مسلسلی نهم با جواب دادهشده آن در زیر دقت کنید تا مراحل انجام این کار را فراگیرید.
مثال: حاصل عبارت زیر را بهدست آورید.
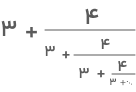
جواب: برای تعیین جواب، ابتدا عبارت بالا را برابر با x قرار میدهیم:
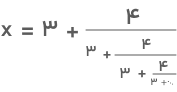
میدانیم که این عبارت انتها ندارد و نامتناهی است. بنابراین، اگر مخرج جمله دوم را برابر با x قرار دهیم، تغییر قابلتوجهی در حاصل این عبارت ایجاد نخواهد شد. بهعبارتی، این کار تأثیری در جواب ما نخواهد داشت. در این صورت داریم:
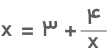
اکنون با اندکی جابهجایی، به معادله زیر میرسیم:
x۲ – ۳x -۴ = ۰
x -۴ ) ( x +۱) = ۰ )
با توجه به معادله بالا، x میتواند برابر با ۴ یا ۱- باشد. اگر x را برابر با ۴ یا ۱- قرار دهید، خواهید دید که هر دو در معادله صدق میکنند و در صورت چهارگزینهای بودن سوال میتوانید حاصل عبارت را بهراحتی تعیین کنید.
نمونه سوالات کسر های مسلسلی با جواب
برای فهم بهتر مطالب، نمونه سؤالهای حلشدهای در قالب pdf آوردهایم. برای مشاهده pdf کسرهای مسلسلی حلشده میتوانید روی لینک زیر کلیک کنید.
سخن پایانی
در این مقاله، نحوه تبدیل کسر ساده به کسر مسلسلی و بالعکس را آموزش دادیم و گفتیم که کسرهای مسلسلی در دو نوع متناهی و نامتناهی وجود دارند. در کسرهای مسلسلی، تفکیک عدد بهصورت مجموع عدد صحیح و کسری فرایندی تکراری است که درصورت خاتمه یافتن، آن را متناهی و در غیر این صورت آن را نامتناهی میگویند. شما میتوانید با حل نمونه سؤالهای گوناگون و مطالعه pdf نمونه سؤالهایی که در این مقاله قرار دادهایم این مبحث را عمیقتر یاد بگیرید.