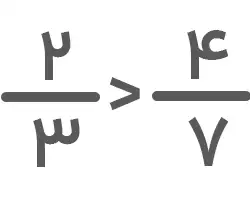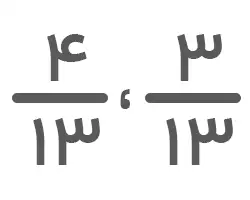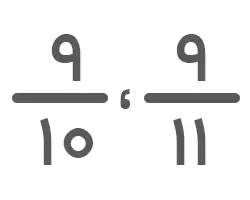مقایسه ی کسرها | آموزش ساده + نمونه سؤال کلاس چهارم تا ششم

در ریاضی کسرها نشان‌دهنده جزء از کل هستند و از دو بخش صورت و مخرج تشکیل شده‌اند. با توجه به این موضوع، زمانی که می‌خواهیم دو یا چند کسر را با هم مقایسه کرده و کسری را انتخاب کنیم که مقدار آن بزرگ‌تر یا کوچک‌تر است، باید یک‌سری قوانین را در نظر بگیریم.

در این آموزش قصد داریم روش‌ها و قواعدی را که برای مقایسه ی کسرها به‌کار می‌رود همراه با حل مثال آموزش دهیم.

مقایسه ی کسر چیست؟

هدف از مقایسه ی کسرها تعیین کسر بزرگ‌تر و کوچک‌تر است. بنابراین، وقتی از مقایسه کردن دو یا چند کسر صحبت می‌کنیم، منظورمان مشخص کردن کسر بزرگ‌‌تر و کوچک‌تر با استفاده از یک‌سری قوانین و روش‌های کاربردی است.

در ادامه نحوه مقایسه دو یا چند کسر را توضیح خواهیم داد. 

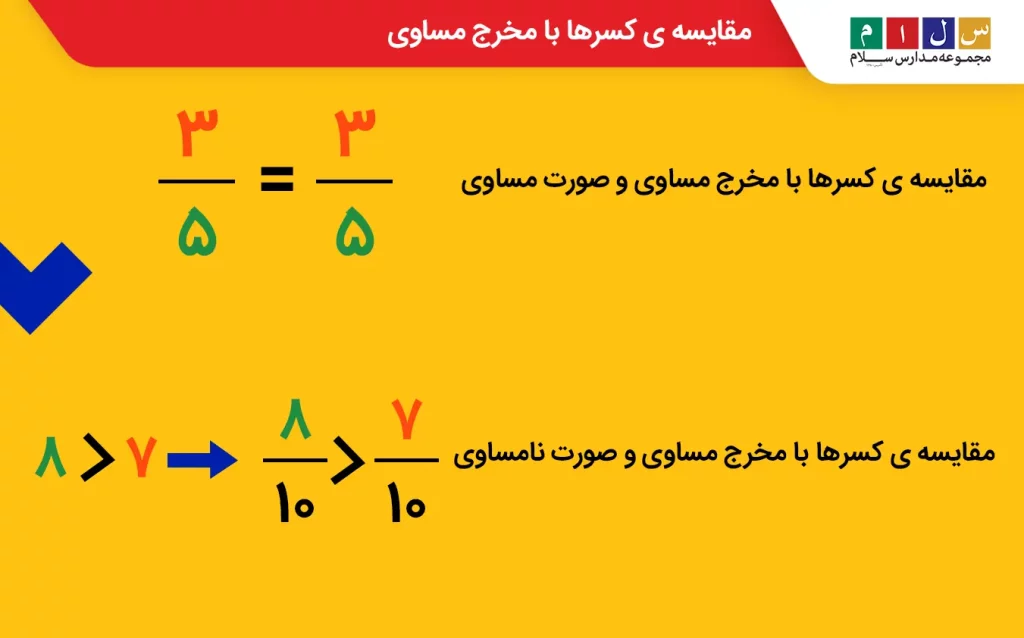
مقایسه ی کسرها با مخرج مساوی

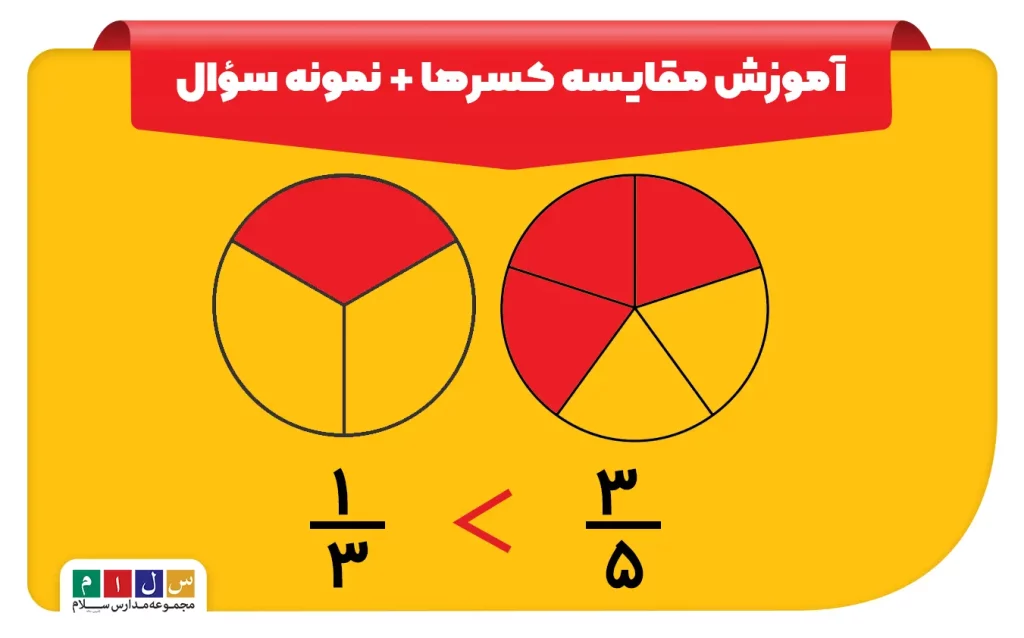
مقایسه کسرهایی که مخرجشان مساوی است، کار بسیار راحتی است. کافی‌ست مقدار صورت‌ها را بررسی کنیم. در اینجا دو حالت خواهیم داشت:

• اگر صورت‌ها مساوی باشند، کسرها نیز مساوی‌اند.
• اگر صورت‌ها نامساوی باشند، کسری که مقدار صورت آن بیشتر است، کسر بزرگ‌تر خواهد بود.

در تصویر زیر، مثال‌هایی از هر دو حالت آورده شده است.

مقایسه کسرها با صورت و مخرج نامساوی و متفاوت

اگر بخواهیم کسرهایی را مقایسه کنیم که مخرج آن‌ها متفاوت است، ابتدا باید مخرج‌ها را با تعیین ک م م آن‌ها به مخرج‌های مشابه تبدیل تبدیل کنیم. پس از یکسان کردن مخرج‌ها می‌توانیم به‌راحتی کسر بزرگ‌تر و کوچک‌تر را تشخیص دهیم.

به‌عنوان مثال، فرض کنید می‌خواهیم دو کسر را با هم مقایسه کنیم. قبل از هر چیز به مخرج‌ها نگاه می‌کنیم تا ببینیم مساوی هستند یا نه. می‌بینیم که مقدار مخرج‌ها متفاوت است. برای اینکه آن‌ها را مساوی کنیم، ابتدا ک م م (کوچک‌ترین مضرب مشترک) آن‌ها را پیدا می‌کنیم.
ک م م ۳ و ۷ برابر با ۲۱ است. بنابراین باید صورت و مخرج دو کسر را در عددی ضرب کنیم که مخرج آن‌ها مساوی ک م م یعنی ۲۱ شود. خواهیم داشت:

$$\frac{۲}{۳}=\frac{۲\times <!--\; \times \; -->۷}{۳\times <!--\; \times \; -->۷}=\frac{۱۴}{۲۱}$$ $$\frac{۴}{۷}=\frac{۴\times <!--\; \times \; -->۳}{۷\times <!--\; \times \; -->۳}=\frac{۱۲}{۲۱}$$

اکنون دو کسر با مخرج مساوی داریم. برای مقایسه دو کسر باید به صورت‌ها توجه کنیم. همان‌طور که گفتیم، در کسرهای با مخرج مساوی کسری بزرگ‌تر است که صورت آن بزرگ‌تر باشد، در اینجا هم چون عدد ۱۴ از ۱۲ بزرگ‌تر است، پس کسر هم از کسر بزرگ‌تر است. درنتیجه:

مقایسه ی کسرها با صورت مساوی

اگر مخرج کسرها نامساوی اما صورت‌ها مساوی باشند، می‌توانیم با بررسی مخرج‌ها به‌راحتی کسرها را مقایسه کنیم. در این حالت، برخلاف حالتی که مخرج‌ها مساوی بودند، کسری بزرگ‌تر خواهد بود که مخرج آن کوچک‌تر است.

به‌عنوان مثال، کسر از کسر بزرگ‌تر است.

مقایسه ی کسرها با روش اعشاری

در این روش، کسرها را با تقسیم صورت بر مخرج یا با استفاده از سایر روش‌های تبدیل کسر به اعشار که در مقاله تبدیل کسر به اعشار توضیح داده ایم، به‌صورت عدد اعشاری می‌نویسیم. سپس، آن‌ها را با هم مقایسه می‌کنیم. هر کدام از اعداد اعشاری بزرگ‌تر باشد، کسر معادل آن هم بزرگ‌تر خواهد بود. 

به‌عنوان مثال، برای مقایسه دو کسر کافی‌ست اعداد اعشاری معادل آن‌ها را تعیین کنیم. عدد اعشاری معادل  مساوی با ۰/۲۵ و عدد اعشاری معادل برابر با ۰/۶۲۵ است. از آنجا که ۰/۶۲۵ از ۰/۲۵ بزرگ‌تر است، کسر هم از کسر  بزرگ‌تر خواهد بود. 

۰/۶۲۵>۰/۲۵

مقایسه ی کسرها با طرفین وسطین

استفاده از ضرب متقاطع یا همان طرفین وسطین یکی دیگر از روش‌های مقایسه کسرها است. در این روش، باید صورت کسر اول را در مخرج کسر دوم و صورت کسر دوم را در مخرج کسر اول ضرب کرده و حاصل آن‌ها را با هم مقایسه کنیم. 

کسرهای را در نظر بگیرید. برای مقایسه این دو کسر، مانند آنچه در تصویر زیر مشاهده می‌کنید صورت کسر اول را در مخرج کسر دوم ضرب کرده و حاصل آن یعنی ۴۴ را زیر کسر اول می‌نویسیم. سپس، صورت کسر دوم را نیز در مخرج کسر اول ضرب کرده و مقدار حاصل یعنی ۵۴ را زیر کسر دوم یادداشت می‌کنیم.

اکنون نوبت مقایسه مقادیر به‌دست‌آمده است. با توجه به اینکه عدد ۵۴ از ۴۴ بزرگ‌تر است، نتیجه می‌گیریم که 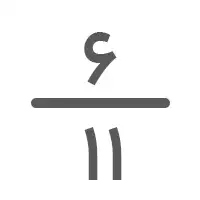هم از بزرگ‌تر است.

نمونه سؤال مقایسه ی کسرها

کسرهای زیر را با هم مقایسه کنید.

1. 
2. 
3. 
4. 

برای مقایسه کسرهای داده‌شده ابتدا مخرج‌ها و سپس صورت‌ها را بررسی می‌کنیم.

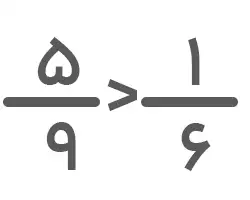
۱. مخرج کسرهای مشابه هم هستند. پس باید صورت‌ها را با هم مقایسه کنیم. از آنجا که ۳<۴ است، خواهیم داشت:

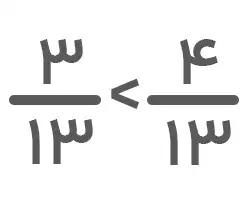
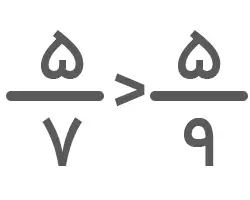
۲. با توجه به اینکه مخرج کسرهای متفاوت و صورت آن‌ها یکسان است، کسری بزرگ‌تر خواهد بود که مخرج آن کوچک‌تر باشد. درنتیجه داریم:

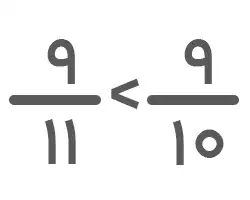
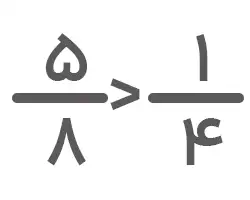
۳. در این مثال، مقدار صورت و مخرج دو کسر با هم فرق دارد. برای مقایسه دو کسر با صورت و مخرج نامساوی باید با کمک ک م م مخرج‌ها کاری کنیم که مقدار آن‌ها مساوی شود. ک م م مخرج‌ها یعنی ۹ و ۶ برابر یا ۱۸ است. این یعنی اینکه باید مخرج کسرها را به ۱۸ تبدیل کنیم. خواهیم داشت:

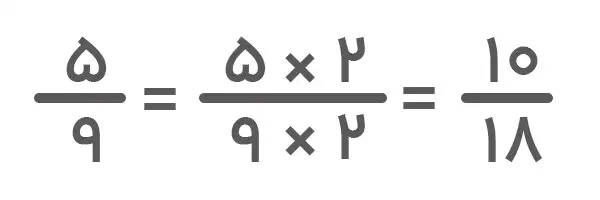
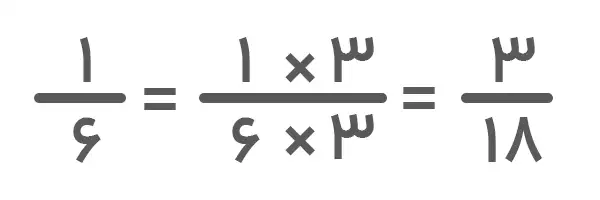
حالا دو کسر با مخرج مساوی داریم که می‌توانیم با بررسی صورت‌های آن‌ها کسر بزرگ‌تر را مشخص کنیم. با توجه به اینکه 10>۳ است، نتیجه مقایسه دو کسر به‌صورت زیر خواهد بود:

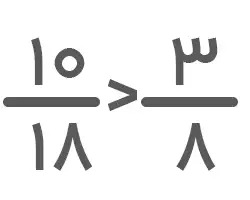
۴. در این مثال، یک کسر و یک عدد مخلوط داریم. برای اینکه بتوانیم آن‌ها را مقایسه کنیم، کافی‌ست ابتدا عدد مخلوط را به کسر تبدیل کنیم.

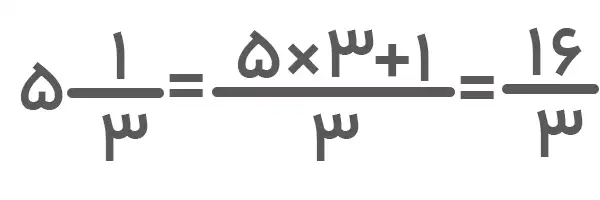
همان‌طور که می‌بینید، عدد مخلوط به کسری مساوی با کسر داده‌شده تبدیل شد. بنابراین، عدد مخلوط و کسر داده‌شده با هم برابرند.

سخن پایانی

در این مطلب، روش‌های مقایسه ی کسرهای نامساوی را توضیح دادیم. به‌طور کلی، اگر بخواهیم کسرها را مقایسه کنیم ابتدا باید مخرج‌ها را مورد بررسی قرار دهیم که آیا مساوی هستند یا نه. برای مقایسه کسرها با صورت و مخرج متفاوت نخستین کاری که باید انجام دهیم، مشخص کردن ک م م و یکسان‌سازی کسرها با استفاده از آن است که با حل مثال شیوه انجام آن را آموزش دادیم. برای یادگیری بهتر این مبحث، خوب است که در کنار مطالعه این مقاله نمونه سؤال‌های متنوع و بیشتری حل کنید.