مثلث اگرچه با کمترین تعداد پاره‌خط (ضلع) ساخته میشود، اما محاسبه مساحتش دست‌کمی از اشکال پیچیده هندسی ندارد. فراوانی تعداد روش‌ها و فرمولهای مساحت مثلث بهترین شاهد این پیچیدگی‌ست. البته نگران نباشید! فرمول‌ها و روش‌های آسانی هم برای محاسبه سطح داخلی مثلث وجود دارد که دانش‌آموزان در سال‌های چهارم و پنجم ابتدایی با آنها آشنا میشوند. ما از این فرمولهای ساده شروع می‌کنیم و با حل مثالهای متنوع، به‌سراغ دیگر روش‌های محاسبه مساحت مثلث می‌رویم و یه گام دیگر به‌سمت تکمیل مباحث محیط و مساحت اشکال هندسی پیش می‌رویم.
شاید بد نباشد قبل از آن سری هم به مطلب مساحت چیست بزنید.
مثلث چیست؟
همه ۳ضلعی‌های بسته مثلث‌اند. منظور از بسته این است که هر ۳ضلع مثلث باید یکدیگر را قطع یا لمس کنند. پس مثلث شکل بسته‌ای است که به‌ازای هر ضلعش، یک راس و زاویه هم دارد. مثل شکل زیر:
اطلاعات موردنیاز برای محاسبه مساحت مثلث
بستگی دارد از کدام فرمول استفاده کنیم. در مهم‌ترین و رایجترین فرمول مساحت به ۲مورد زیر نیاز داریم:
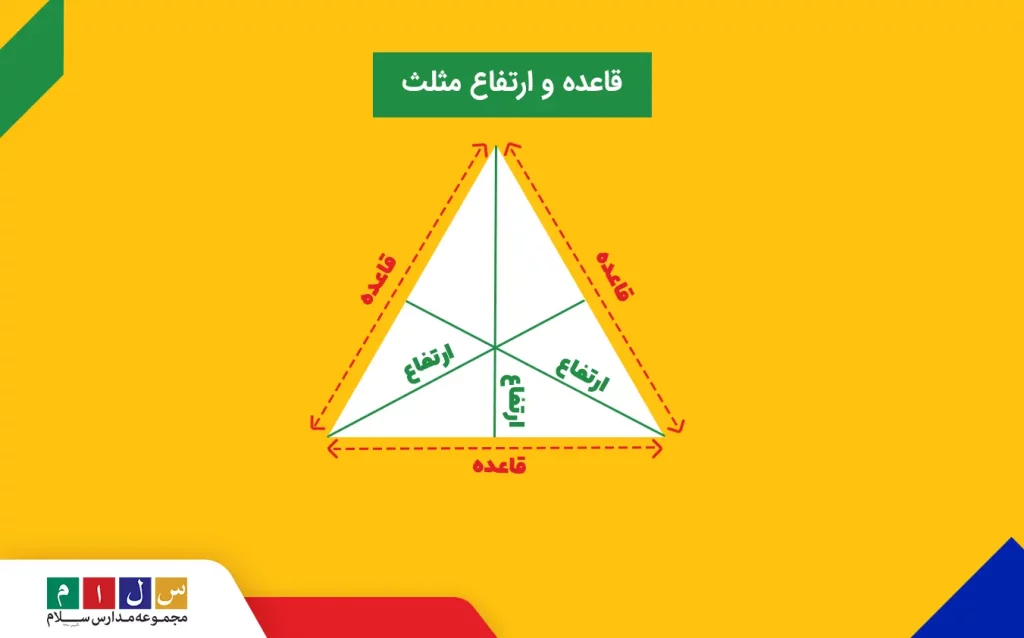
- ارتفاع: اگر از راس مثلث یک «پاره‌خطِ عمود بر ضلع مقابل» رسم کنیم، نام آن پاره‌خط ارتفاع مثلث است.
- قاعده: ضلعی که مقابل راس قرار دارد و پاره‌خط بر آن عمود میشود، قاعده نام دارد.
فرمول مساحت مثلث
روش زیر، پرکاربردترین فرمول مساحت مثلث است:
۲÷ قاعده × ارتفاع = مساحت مثلث
A = h × b ÷ ۲
- h: ارتفاع
- b: قاعده
مثال: ارتفاع و قاعده یک پل مثلثی‌شکل به‌ترتیب ۳ و ۲ سانتی‌متر است، مساحت آن را حساب کنید.
۲ ÷ قاعده × ارتفاع = مساحت مثلث
A= ۳ × ۲ ÷ ۲ = ۶ ÷ ۲= ۳
رابطه بین مساحت مثلث و دیگر اشکال هندسی
به‌طرز جالب و شگفت‌انگیزی می‌توان تمام اشکال هندسی را به چند مثلث تبدیل کرد. به‌عنوان‌مثال، از درون مربع می‌توان بی‌نهایت مثلث در آورد. به‌شکل زیر نگاه کنید:
حالا اگر ۲راس دیگر را هم به یکدیگر وصل کنیم، از درون این مربع ۴ مثلث بیرون می‌آید:
حالا اگر از وسط هر ضلع یک پاره‌خط به ضلع مقابلش رسم کنیم، تعداد مربع‌ها دوبرابر میشود و این کار را می‌توان تا بی‌نهایت ادامه داد.
نکته‌ی بالا اهمیت زیادی دارد و در حل مسائل هندسی به کارتان می‌آید، زیرا مساحت برخی از اشکال هندسی را فقط با تبدیل آنها به یک یا چند مثلث می‌توان محاسبه کرد.
روش های محاسبه مساحت انواع مثلث ها
مثلث‌ها انواع مختلفی دارند:
- متساوی‌الاضلاع
- متساوی‌الساقین
- قائم‌الزاویه
- منفرجه
- مختلف‌الاضلاع
به‌دلیل تفاوت‌هایی که بین این مثلث‌ها وجود دارد، روش‌های محاسبه مساحتشان هم تاحدودی متفاوت‌اند. در ادامه روش محاسبه مساحت هرکدامشان را بهصورت جداگانه توضیح می‌دهیم:
مساحت مثلث متساوی الاضلاع
مثلثی که تمام اضلاع آن با یکدیگر برابر باشند را مثلث متساوی‌الاضلاع می‌گوییم. علاوه‌بر فرمول اصلی مساحت مثلث، برای محاسبه مساحت مثلث متساوی الاضلاع می‌توان از فرمول زیر هم استفاده کرد:
اندازه یک‌ضلع به‌توان ۲ × ۴ ÷ جذر ۳ = مساحت مثلث متساوی‌الاضلاع
A= √۳/۴ × a²
- A: مساحت مثلث
- a: اندازه یک‌ضلع (توجه داشته باشید که اندازه اضلاع متساوی‌الاضلاع برابر است، پس فرقی ندارد اندازه کدام ضلع را حساب کنیم)
مساحت مثلث متساوی الساقین
مثلث متساوی‌الساقین دارای ۲ ضلع مساوی‌ست. اگر اندازه‌ی این ۲ ساقِ مساوی و قاعده مثلث متساوی‌الساقین را داشته باشیم، می‌توانیم به‌کمک فرمول زیر، به‌راحتی مساحت مثلث متساوی الساقین را محاسبه کنیم:
قاعده × (4 ÷ قاعده به‌توان ۲ × اندازه یکی از ساق‌ها به‌توان ۲) جذر × یک دوم = مساحت مثلث متساوی الساقین
A=1÷۲ × { √a² × b² ÷۴ × b }
- a: اندازه‌ی یکی از ساق‌ها
- b: اندازه قاعده یا همان ضلع نامساوی با ۲ضلع دیگر
مساحت مثلث قائم الزاویه
به مثلثی که یک زاویه ۹۰درجه و ۲زاویه ۴۵درجه داشته باشد، مثلث قائم‌الزاویه می‌گویند. نکته جالبی درباره مثلث قائم‌الزاویه وجود دارد که در محاسبه مساحت مثلث قائم الزاویه کمک زیادی به شما می‌کند:
- ضلع‌های مجاورِ زاویه ۹۰درجه، قاعده و ارتفاع یکدیگر به حساب می‌آیند، یعنی هرکدام آنها را قاعده بگیرید، دیگری ارتفاع است و برعکس.
پس برای محاسبه مساحت مثلث قائم‌الزاویه می‌توانیم از این فرمول ساده استفاده کنیم:
۲ ÷ ضرب اضلاع مجاور زاویه قائمه در یکدیگر = مساحت مثلث قائم‌الزاویه
مساحت مثلث منفرجه
یکی از زوایای مثلث منفرجه بیش از ۹۰درجه است و همین‌مسئله کار را برای محاسبه مساحتش سخت می‌کند. به‌دلیل زاویه منفرجه، نمی‌توان خطی عمود بر ضلع مقابل کشید و مساحت مثلث منفرجه را محاسبه کرد. برای محاسبه مساحت مثلث منفرجه باید آن را به مثلث قائم‌الزاویه تبدیل کرد:
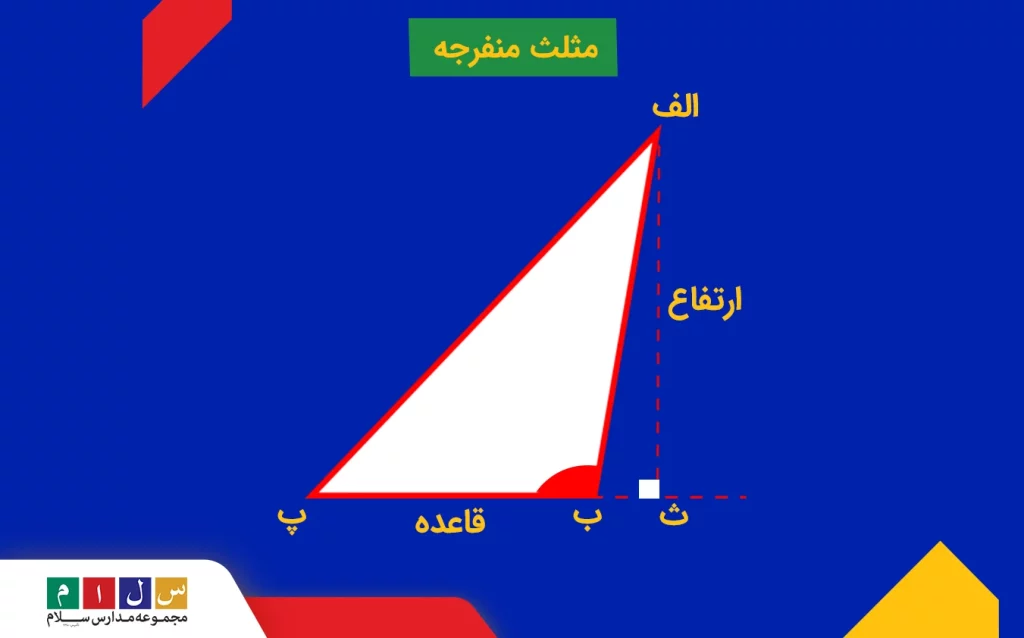
در این تصویر از ضلع مجاور زاویه منفرجه، خطی عمود بر دیگر ضلع مجاور زاویه منفرجه رسم می‌کنیم. آن خط (الف-ث) مساوی‌ست با ارتفاع مثلث. در این حالت، ضلع مجاور (ب-پ) قاعده مثلث محسوب میشود. حالا که قاعده و ارتفاع را به دست آوردیم، می‌توانیم به‌کمک فرمول اصلی مثلث (قاعده ضربدر ارتفاع تقسیم بر ۲)، مساحت مثلث منفرجه را حساب کنیم.
مساحت مثلث مختلف الاضلاع
وقتی اندازه‌ی ضلع‌های یک مثلث با یکدیگر متفاوت باشند، به آن مثلث مختلف‌الاضلاع می‌گویند. راحت‌ترین روش برای محاسبه مساحت مختلف‌الاضلاع، همان فرمول اصلی «طول ضربدر قاعده تقسیم بر ۲» است. بسته به اطلاعات صورت سوال، از دیگر فرمولهای محاسبه مساحت مثلث مانند فرمول هرون و مثلثات هم می‌توان استفاده کرد. این فرمول‌ها را در قسمت‌های بعدی این مقاله توضیح دادهایم.
چگونه مساحت مثلث را حساب کنیم با مثال
حالا که فرمول اصلی مساحت مربع را یاد گرفتیم، بیایید قبل از رفتن به‌سراغ دیگر فرمولهای مساحت مثلث و پیچیدگی‌های آنها، این فرمول را با مثالهای فراوان در ذهن خود تثبیت کنیم.
مثال اول | محاسبه مساحت مثلث مختلف الاضلاع
ارتفاع و قاعده مثلثی به‌ترتیب ۱۰ و ۷سانتی‌متر است. مساحت این مثلث چندسانتی‌متر است؟
جواب: همان‌طور که گفتیم، برای محاسبه مساحت مثلث مختلف‌الاضلاع بهتر است از فرمول اصلی (ارتفاع ضربدر قاعده تقسیم بر ۲) استفاده کنیم. باتوجه به مقادیر ارائهشده در صورت سوال و فرمول مساحت مثلث خواهیم داشت:
A=h × b ÷ ۲
۲ ÷ قاعده × ارتفاع = مساحت مثلث مختلف الاضلاع
۲ ÷ ۷ × ۱۰ = مساحت مثلث مختلف الاضلاع
۳۵ =۲ ÷ ۷۰ = مساحت مثلث مختلف الاضلاع
مثال دوم | محاسبه مساحت مثلث متساوی الاضلاع
یک آینه مثلثی‌شکل با ۳ ضلع مساوی داریم. می‌خواهیم این آینه را به دیوار اتاق خواب میخ کنیم، اما قبل از آن باید بدانیم مساحت آن چقدر است. اگر ارتفاع و قاعده‌ی این آینه به‌ترتیب 6 و 5 سانتی‌متر باشند، آینه مثلثی‌شکل چه مقدار از فضای دیوار اتاق را اِشغال می‌کند؟
جواب: باتوجه به اینکه ۳ضلع مثلث بایکدیگر مساوی‌اند، پس با مثلثی متساوی‌الاضلاع روبه‌رو هستیم. برای محاسبه مساحت متساوی‌الاضلاع از ۲ فرمول می‌توان استفاده کرد:
- فرمول اصلی مساحت مثلث
- فرمول مختص به مساحت مثلث متساوی‌الاضلاع (این فرمول برای مقاطع تحصیلی بالاتر از دبستان است)
طبق فرمول اصلی خواهیم داشت:
A = h × b ÷۲باتوجه به اینکه قاعده یکی از ضلع‌های مثلث است و در فرمول اختصاصی محاسبه مساحت مثلث متساوی‌الاضلاع، به‌اندازه‌ی یکی از ضلع‌ها نیاز داریم، برای محاسبه مساحت متساوی‌الاضلاع با این فرمول خواهیم داشت:
دلیل کمی تفاوت در نتیجه به‌دست‌آمده به فرضی‌بودن اعداد بر می‌گردد و در دنیای واقعی هر ۲ فرمول به یک نتیجه می‌رسند.
مثال سوم: محاسبه مساحت مثلث متساوی‌الساقین
ارتفاع و قاعده یک مثلث متساوی‌الساقین به‌ترتیب ۱۲ و ۳ سانتی‌متر و اندازه یکی از ساق‌های آن ۸ سانتی‌متر است. مساحت این مثلث را حساب کنید.
جواب: باتوجه به اینکه علاوه‌بر قاعده و ارتفاع، اندازه ساق‌های مثلث را هم داریم، از ۲ فرمول زیر می‌توانیم برای محاسبه مساحت مثلث استفاده کنیم:
- فرمول رایج مساحت مثلث
- فرمول مختص به مساحت مثلث متساوی‌الساقین (این فرمول برای مقاطع تحصیلی بالاتر از دبستان است)
براساس فرمول پرکاربرد مساحت مثلث خواهیم داشت:
A= h × b ÷ ۲
2÷ قاعده × ارتفاع = مساحت مثلث متساوی الاضلاع
۲÷ ۳ × ۱۲ = مساحت مثلث متساوی الاضلاع
۱۸ = ۲ ÷ ۳۶ = مساحت مثلث متساوی الاضلاع
باتوجه به اینکه اندازه ساق‌های مثلث را هم داریم، استفاده از فرمول منحصربه‌فرد مثلث متساوی‌الساقین هم امکان‌پذیر است:
A= 1÷ 2 × { √a² × b² ÷ 4 × b }
قاعده × (4 ÷ قاعده به‌توان ۲ × اندازه یکی از ساق‌ها به‌توان ۲) جذر × یک‌دوم = مساحت مثلث متساوی‌الساقین
۳ × (۴ ÷ ۳ به‌توان ۲ × ۸ به‌توان ۲) جذر × یک‌دوم = مساحت مثلث متساوی‌الساقین
۳ × (۴ ÷ ۹ ×۶۴) جذر × یک‌دوم = مساحت مثلث متساوی‌الساقین
۳ × (۴ ÷ ۹ × ۶۴) جذر × یک‌دوم = مساحت مثلث متساوی‌الساقین
۳ × (۴ ÷ ۹ × ۶۴) جذر × یک‌دوم = مساحت مثلث متساوی‌الساقین
۳ × (۴ ÷ ۹ × ۶۴) جذر × یک‌دوم = مساحت مثلث متساوی‌الساقین
۳ × (۱۲) × یک‌دوم = مساحت مثلث متساوی‌الساقین
۱۸ = ۳۶ × یک‌دوم = مساحت مثلث متساوی‌الساقین
مثال چهارم | محاسبه مساحت مثلث قائم‌الزاویه
اندازه اضلاع مجاور زاویه قائمه در یک مثلث به‌ترتیب ۲ و ۴ سانتی‌متر است. مساحت این مثلث را حساب کنید.
جواب: همان‌طور که گفتیم، دو ضلع مجاور زاویه قائمه در مثلث قائم‌الزاویه، قاعده و ارتفاع یکدیگرند. بااین‌اوصاف می‌توان یکی از این دوضلع را قاعده و دیگری را ارتفاع در نظر گرفت و براساس فرمول اصلی مساحت مثلث به جواب این سوال رسید.
مثال پنجم | محاسبه مساحت مثلث منفرجه
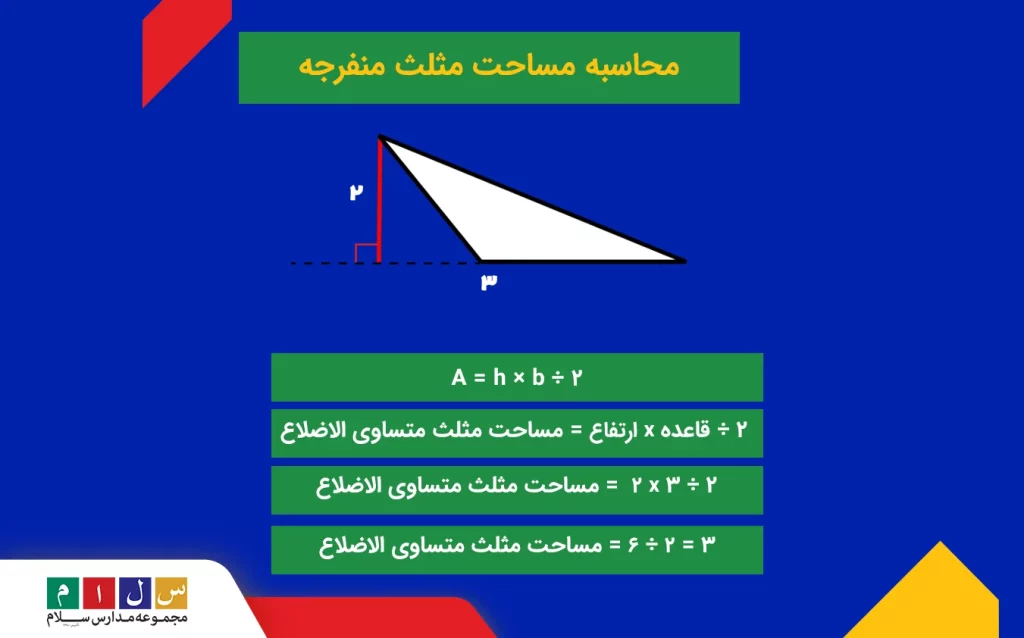
ارتفاع و قاعده یک مثلث منفرجه به‌ترتیب ۲ و ۳ سانتی‌متر است. اندازه مساحت این مثلث چه عددی است؟
جواب: فراموش نکنید که برای پیداکردن ارتفاع مثلث منفرجه باید طبق تصویر زیر، از راس ضلع خارجی زاویه باز مثلث، خطی عمود بر دیگر ضلع مجاور زاویه باز رسم کنید. اندازه این خط عمود مساوی‌ست با ارتفاع مثلث منفرجه. بعد از به‌دست‌آوردن ارتفاع، قاعده آن را هم طبق تصویر زیر حساب و سپس براساس فرمول اصلی مساحت مثلث برای محاسبه اقدام کنید:
A=h×b÷۲
۲ ÷ قاعده × ارتفاع = مساحت مثلث متساوی‌الاضلاع
۲ ÷ ۴ × ۲ = مساحت مثلث متساوی‌الاضلاع
۴ = ۲ ÷ ۸ = مساحت مثلث متساوی‌الاضلاع
مسائل و فرمول‌هایی که در ادامه می‌آیند، برای دانش‌آموزان ابتدایی نیستند. از این مباحث در مقاطع تحصیلی بالاتر استفاده میشود.
روش‌های دیگر محاسبه مساحت مثلث
علاوه‌بر روش‌های پیش‌گفته، برای محاسبه مساحت مثلث چند روش دیگر هم وجود دارد که در ادامه به اختصار درباره‌ی آنها توضیح می‌دهیم:
فرمول هرون
این فرمول حدود ۲۰۰۰ سال پیش توسط یک مهندس و ریاضی‌دان اهل یونان به نام هرون اسکندریه کشف شد. وقتی اندازه ۳ ضلع مثلث را داشته باشیم، می‌توانیم از فرمول هرون استفاده کنیم. فرمول مساحت مثلث بااستفاده از ۳ ضلع به این شرح است:
A = √ s (s – a) × (s – b) × (s – c)
و
S=(a+b+c) ÷ ۲
- s: محیط مثلث تقسیم بر ۲
- a,b,c: اندازه ۳ضلع مثلث
مثال: اگر اندازه ۳ضلع یک مثلث ۴سانتی‌متر باشد، مساحت آن چقدر میشود؟
جواب: اندازه ۳ضلع مثلث را داریم، پس می‌توانیم از فرمول هرون برای رسیدن به جواب استفاده کنیم. اندازه ۳ضلع مثلث یا متغیرهای a,b و c را در صورت مسئله داریم که هر ۳تای آنها ۴سانتی‌متر هستند. پس ابتدا باید مقدار s را حساب کنیم:
S=(a+b+c) ÷ ۲
S= (۴+۴+۴) ÷ ۲ = (۱۲÷۲) = ۶
حالا که مقدار s را حساب کردیم، به‌راحتی مقادیر داده‌شده را در فرمول هرون می‌گذاریم و مساحت مثلث را حساب می‌کنیم:
A = √ s (s – a) × (s – b) × (s – c)
A = √ ۶ (۶ – ۴) × (۶ – ۴) × (۶ – ۴)
A=√ ۶ × ۲ × ۲ × ۲
A = √۴۸ = ۶/۹۲
محاسبه مساحت مثلث با ۲ ضلع و زاویه بین آنها
اگر اندازه ۲ضلع مثلث و زاویه بین آنها را داشته باشیم، فرمول یا ۳ فرمول دیگر هم برای محاسبه مساحت مثلث وجود دارد که به این شرح‌اند:
A= ۱ ÷ ۲(a×b) × sinC
A=۱ ÷ ۲ (b × c) × sinA
A=۱÷۲ (a × c) × sinB
هر سه فرمول بالا در واقع یک فرمول‌اند. تنها چیزی که در بین آنها تفاوت دارد، ۲ضلع و زاویه بینشان است. به‌عنوان‌مثال، اگر اندازه دوضلع a و b و زاویه بین آنها را داشته باشیم، از فرمول اول استفاده می‌کنیم و اگر دوضلع b و c و زاویه بینشان را داشته باشیم، با فرمول دوم پیش می‌رویم.
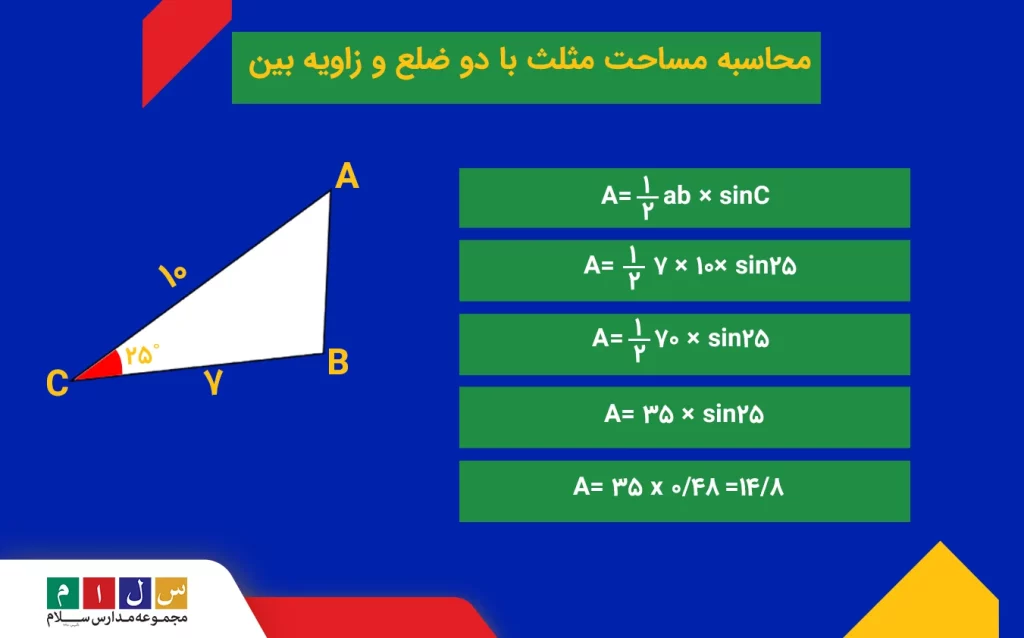
مثال: اگر اندازه ۲ضلع یک مثلث ۷ و ۱۰سانتی‌متر و زاویه بین آنها ۲۵درجه باشد، مساحت این مثلث را محاسبه کنید:
جواب: طبق فرمول‌ها بالا اگر اندازه دوضلع و زاویه بین آنها را داشته باشیم، باید آن دوضلع را ابتدا در هم ضرب، سپس تقسیم بر ۲ و درنهایت در سینوس زاویه بینشان ضرب کنیم:
روش محاسبه مساحت مثلث با دو زاویه و ضلع بین
برای استفاده از این روش ابتدا باید با نحوه نام‌گذاری ضلع‌ها و زوایای مثلث آشنایی کافی داشته باشیم. مثلث دارای ۳ ضلع است که در ریاضی آنها را با حروف انگلیسی a، b و c مشخص می‌کنیم. ضلع‌ها و زاویه‌های روبه‌روی یکدیگر در مثلث‌ها هم‌نام‌اند. به‌عنوان‌مثال، اگر یک‌ضلع مثلث را a بنامیم، زاویه روبه‌روی آن را با A مشخص می‌کنیم. برای درک ملموس این فرآیند به تصویر زیر نگاه کنید:
اگر در مثلث بالا اندازه ۲ زاویه و ضلع بین آنها را داشته باشیم، می‌توانیم از فرمولهای زیر برای رسیدن به جواب استفاده کنیم. دقت کنید که ۳ فرمول داریم، چون ۳ حالت متصور است:
1.اندازه زوایای A و B و ضلع
2.اندازه زوایای A و C و ضلع b
3.اندازه زوایای B و C و ضلع a
هم‌زمان با خواندن این ۳ حالت، به تصویر بالا نگاه کنید و آنها را بهصورت بصری هم درک کنید. براساس این ۳ حالت، ۳ فرمول برای محاسبه مساحت داریم:
۱. A=(c² × sinA × sin B) ÷ ( ۲ × sin c)
۲. A=(b² × sinA × sin C) ÷ (۲ × sin B)
۳. A= (a² × sinB × sin C ) ÷( ۲ × sin A)
- a، b و c: اندازه ضلع‌های مثلث
- A: اندازه زاویه راس A
- B: اندازه زاویه راس B
- C: اندازه زاویه راس C
احتمالا با خودتان بگویید که « وقتی در صورت سوال تنها اندازه ۲ زاویه و ضلع بین آنها آمده است، اندازه زاویه سوم را از کجا پیدا کنم؟». جواب این سوال بسیار ساده است: جمع زوایای داخلی یک مثلث همواره ۱۸۰ درجه است؛ پس اگر اندازه ۲ زاویه را داشته باشیم، به‌راحتی می‌توانیم سومی را پیدا کنیم. به‌عنوان‌مثال:
- اگر اندازه ۲ زاویه در مثلثی ۵۰ و ۷۰ درجه باشد، اندازه زاویه سوم آن ۶۰ درجه است؛ زیرا جمع ۲ زاویه ۱۲۰ درجه میشود که اگر آن را از ۱۸۰ کم کنیم، به عدد ۶۰ می‌رسیم.
حالا و با این توضیحات به‌سراغ حل مثال می‌رویم:
مثال برای محاسبه مساحت مثلث با ۲ زاویه و ضلع بین
اگر اندازه ۲ زاویه B و C در مثلثی به‌ترتیب ۵۰ و ۷۰ و ضلع a بین آنها ۸ سانتی‌متر باشد، مساحت این مثلث را حساب کنید.
جواب: باتوجه به اینکه اندازه ۲ زاویه و ضلع بین آنها را داریم، می‌توانیم از فرمول محاسبه مساحت مثلث به‌کمک سینوس زوایا و ضلع بین آنها استفاده کنیم:
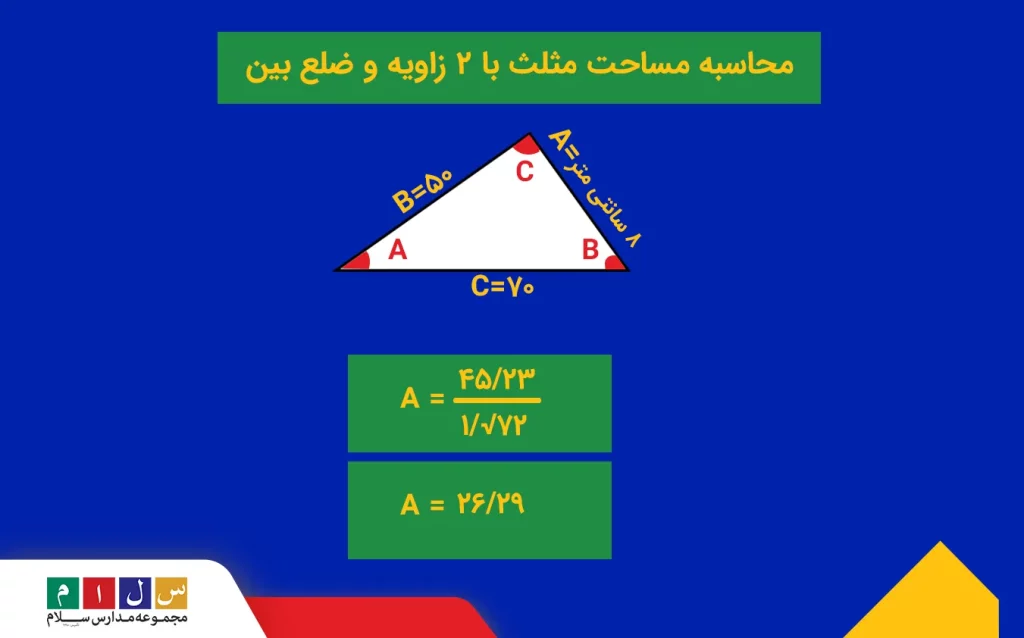
طبق اطلاعات صورت سوال خواهیم داشت:
- a: طول ضلع a ۸ سانتی‌متر
- B: زاویه راس B مساوی‌ست با ۵۰ درجه
- C: زاویه راس C مساوی‌ست با ۷۰ درجه
- A: زاویه راس A مساوی‌ست با ۱۸۰ منهای اندازه ۲زاویه قبل (۱۲۰) که میشود ۶۰ درجه
حالا می‌توانیم مقادیر داده‌شده را در فرمول جای‌گذاری کنیم:
( A= (a² × sinB × sinC) ÷ (۲ × sinA
(A=(8² × sinB × sinC) ÷ (۲ × sinA
(A=(۶۴ × ./۹۳) ÷ (۲ × ./۸۶
A=۴۵/۲۳۱ ÷ 1/۷۲
A=۲۶/۲۹
محاسبه مساحت مثلث با ۲ ضلع و یکی از زوایای مقابل زاویه مجاور
با این ترکیب داده‌ها محاسبه مساحت مثلث امکان‌پذیر نیست، مگر اینکه ابتدا باتوجه اطلاعات در دسترس، اندازه دیگر زوایا و ضلع‌های مثلث را پیدا کنیم و سپس به‌کمک دیگر فرمول‌ها به جواب برسیم. اما چگونه می‌توانیم با داشتن اندازه ۲ ضلع و یک زاویه، اندازه دیگر ضلع‌ها و زوایای مثلث را پیدا کنیم؟ جواب آن در آگاهی از رابطه بین ضلع‌ها و زوایای مثلث براساس قانون سینوس‌ها نهفته است. طبق این قانون خواهیم داشت:
a÷sinA = b÷sinB = c÷sinc
مثال: اگر اندازه ۲ ضلع a و b در مثلثی به‌ترتیب ۶ و ۵ سانتی‌متر و زاویه راس A در این مثلث ۵۵درجه باشد، مساحت دیگر ضلع‌ها و زوایای آن را حساب کنید.
جواب: باتوجه به اینکه اندازه ضلع a و b و زاویه راس A در صورت سوال آمده است، می‌توان باتوجه به نسبت‌های مثلثاتی اندازه دیگر ضلع‌ها و زاویه‌ها را پیدا کرد:
a ÷ sinA = b÷ sinB = c÷ sinc
6تقسیم بر 0/81 برابر است با 5 تقسیم بر sinBبرابر است با c تقسیم بر sinC
5 = sinB × ۷/۴۰
۰/۶۷=۷/۴۰ ÷5=sinB
sinB = ۰/۶۷
۴۲ درجه =B
حالا که اندازه ۲ زاویه را داریم، اندازه زاویه سوم را به‌راحتی حساب می‌کنیم:
۸۳ = (۴۲ + ۵۵) – ۱۸۰
حالا که اندازه ۳زاویه و ۲ضلع مثلث را داریم، می‌توانیم به کمک نسبت‌های مثلثاتی، اندازه ضلع آخر را نیز حساب کنیم:
۷/۴۰ برابر است با c تقسیم بر جذر ۰/۹۹
7/40×0/99=c
c=۷/
حالا که هر ۳ضلع و زاویه را داریم، می‌توانیم از فرمول‌هایی مانند هرون برای به‌دست‌آوردن مساحت مثلث استفاده کنیم.
سخن پایانی
اگرچه مثلث فقط یک ۳ ضلعی‌ست و به‌ظاهر پیچیدگی چندانی ندارد، اما همان‌طور که دیدیم، بین ضلع‌ها و زوایای آن روابط پیچیده‌ای وجود دارد. این پیچیدگی‌ها اگرچه با محاسبات سخت ریاضی همراه است، اما یادگیری آنها برای قوی‌شدن پایه مثلثات و هندسه دانش‌آموزان اهمیت دارد. ما دراینجا از رایجترین فرمول محاسبه مساحت مثلث یعنی «ارتفاع ضربدر قاعده تقسیم بر ۲» شروع و با مثالهای فراوان و متنوع، به‌سمت روش‌های محاسبه انواع مختلف مثلث حرکت کردیم. همچنین درباره فرمول هرون و محاسبه مساحت مثلث به کمک زوایا و روابط مثلثاتی هم توضیحاتی ارائه کردیم. هرکدام از این فرمول‌ها در شرایط خاصی کاربرد دارد و دانستن آنها به‌خصوص برای علاقه‌مندان به رشته ریاضی نهم مفید است.
سوالات متداول
- فرمول مساحت مثلث چیست؟
برای محاسبه مساحت مثلث از فرمولهای زیادی استفاده میشود که رایجترین آنها فرمول «ارتفاع ضربدر قاعده تقسیم بر ۲» است. ما این فرمول و دیگر فرمولهای محاسبه مساحت مثلث را با ذکر مثال در متن مقاله آوردهایم.. - مساحت مثلث را چگونه حساب کنیم؟
به نوع مثلث و اطلاعات ارائهشده در صورت سوال بستگی دارد. ما در متن مقاله هم نحوه محاسبه مساحت انواع مثلث و هم نحوه شناسایی فرمول مناسب را با مثالهای فراوان توضیح دادهایم. - مساحت مثلث در کلاس چهارم چیست؟
بچههای ابتدایی مساحت انواع مثلث را در پایه چهارم میآموزند. آنها در این پایه با فرمول اصلی مساحت مثلث یعنی «قاعده ضربدر ارتفاع تقسیم بر ۲» آشنا میشوند. ما در این مقاله مساحت مثلث را بهصورت مفهومی و با مثال از سطح ابتدایی تا پیشرفته توضیح دادهایم..
