ضرب مساحتی یک روش کاربردی برای ساده کردن فرآیند ضرب به‌ویژه ضرب اعداد بزرگ‌تر است. این روش، به دانش‌آموزان کمک می‌کند تا مفهوم ضرب را به‌صورت بصری درک کنند.
برای اینکه با این روش بیشتر آشنا شوید، در این مقاله به آموزش ضرب مساحتی می‌پردازیم و با تمرین‌های کاربردی، روش انجام آن را توضیح می‌دهیم. پیشنهاد می‌کنم مقالات قبلی ما، مانند آموزش جدول ضرب برای کودکان را هم مطالعه کنید.
ضرب به روش مساحتی
ضرب مساحتی یک نمایش تصویری از ضرب است که حاصل‌ضرب اعداد را به‌صورت مساحت مستطیل نشان می‌دهد. در روش ضرب مساحتی، برای درک بهتر حاصل‌ضرب، اعداد براساس ارزش مکانی تجزیه شده و شکل مستطیل به واحدهای کوچک‌تر تقسیم می‌شود. در بخش‌های بعدی، مراحل انجام ضرب مساحتی را برای اعداد دورقمی و سه‌رقمی توضیح خواهیم داد.
پیشنهاد مطالعه: ایده‌هایی برای آموزش جدول ضرب با بازی
ضرب مساحتی دو رقمی در یک رقمی
فرض کنید می‌خواهیم حاصل‌ضرب ۶۵۷ را به‌دست آوریم. برای انجام این کار باید مراحل زیر را طی کنیم:
- مرحله ۱: ابتدا اعداد را با توجه به ارزش مکانی ارقام آن‌ها گسترده نویسی می‌کنیم. با این کار، فرایند ضرب اعداد آسان‌تر می‌شود. بنابراین، اگر بخواهیم عدد ۶۵ را به‌صورت گسترده بنویسیم، خواهیم داشت:
۶۵=۶۰+۵
- مرحله ۲: یک مستطیل رسم می‌کنیم که طول آن ۶۵ و عرض آن ۷ باشد.
- مرحله ۳: مانند شکل زیر، طول مستطیل را به‌گونه‌ای تقسیم می‌کنیم که شکل گسترده عدد ۶۵ را به‌خوبی نشان دهد.
- مرحله ۴: مساحت هر یک از مستطیل‌ها را که برابر با مقدار طول ضربدر عرض است، محاسبه می‌کنیم و در داخل مستطیل‌ها می‌نویسیم.
- مرحله ۵: مساحت به‌دست‌آمده مستطیل‌ها را با هم جمع می‌کنیم.
۴۲۰ + ۳۵ = ۴۵۵
بنابراین، می‌توان نتیجه گرفت حاصل‌ضرب دو عدد که برابر با مساحت مستطیل بزرگ است، مساوی است با
۶۵ × ۷ = ۴۵۵
ضرب مساحتی دو رقمی در دو رقمی
در این بخش، مراحل انجام ضرب مساحتی دو عدد دورقمی ۷۹ × ۵۲ را بیان می‌کنیم.
- مرحله ۱: ابتدا شکل گسترده دو عدد را به‌صورت زیر می‌نویسیم:
۵۲ = ۵۰+۲
۷۹ = ۷۰+۹
- مرحله ۲: یک مستطیل به‌طول ۷۹ و عرض ۵۲ رسم می‌کنیم.
- مرحله ۳: مستطیل را به مستطیل‌هایی کوچک‌تر با ابعادی که در مرحله اول مشخص کردیم، تقسیم می‌کنیم.
- مرحله ۴: مساحت هر کدام از مستطیل‌ها را به‌طور جداگانه تعیین کرده و یادداشت می‌کنیم.
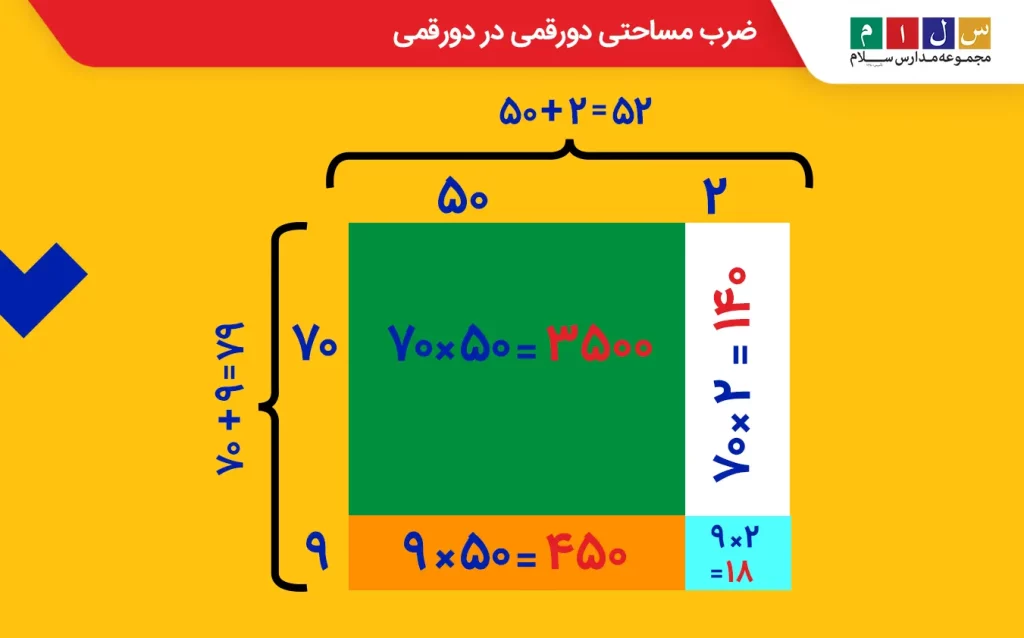
- مرحله ۵: مساحت‌های به‌دست‌آمده در مرحله قبل را با هم جمع می‌زنیم.
۳۵۰۰ + ۱۴۰ + ۴۵۰ + ۱۸ = ۴۱۰۸
بنابراین، حاصل‌ضرب اعداد داده‌شده برابر است با
۵۲ × ۷۹ = ۴۱۰۸
ضرب مساحتی سه رقمی در دو رقمی
برای انجام ضرب مساحتی عدد سه‌رقمی در عدد دورقمی، اعداد را گسترده‌نویسی کرده و یک مستطیل با ابعاد داده‌شده رسم می‌کنیم.
برای مثال، حاصل‌ضرب ۸۱ × ۲۴۸ ضرب مساحتی را به صورت زیر انجام می دهیم :
۲۴۸ = ۲۰۰ + ۴۰ + ۸
۸۱ = ۸۰ + ۱
بنابراین، حاصل‌ضرب ۲۴۸ × ۸۱ که برابر با مجموع مساحت مستطیل‌هاست، مساوی است با
۲۴۸ × ۸۱ = ۱۶۰۰۰ + ۳۲۰۰ + ۶۴۰ + ۲۰۰ + ۴۰ + ۸ = ۲۰۰۸۸
اولین نفری باشید که از اخبار و اطلاعیه‌های مرتبط با پایه تحصیلیتان باخبر می‌شود!
ضرب مساحتی اعداد مخلوط را چگونه محاسبه کنیم؟
اعداد مخلوط اعدادی هستند که از یک بخش عدد صحیح و یک بخش کسری تشکیل شده‌اند. ضرب مساحتی این اعداد مشابه ضرب مساحتی اعداد طبیعی که در بخش‌های قبل با آن آشنا شدیم انجام می‌شود.
با یک مثال، روش انجام ضرب این اعداد را به روش مساحتی توضیح می‌دهیم.
اعداد زیر را در نظر بگیرید.
برای اینکه این دو عدد را در هم ضرب کنیم، ابتدا یک مستطیل با این ابعاد رسم می‌کنیم و سپس، طول و عرض آن را مانند تصویر زیر به‌گونه‌ای تقسیم می‌کنیم که بخش صحیح و کسری عدد مخلوط از هم جدا شود.
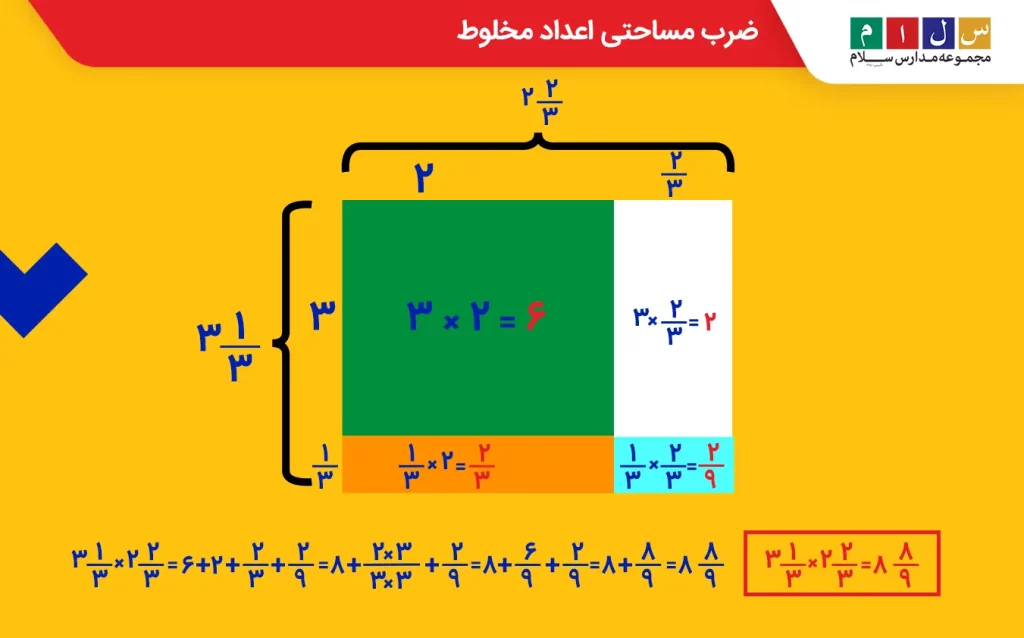
اکنون مساحت چهار مستطیل را جداگانه محاسبه کرده و با هم جمع می‌کنیم تا مقدار مساحت مستطیل بزرگ یا به‌عبارتی حاصل‌ضرب دو عدد مخلوط به‌دست آید.
پیشنهاد مطالعه: آموزش تبدیل کسر به عدد مخلوط
ضرب مساحتی اعداد کسری چیست؟
برای انجام ضرب مساحتی کسرهای بزرگ‌تر از واحد کافی‌ست کسرها را به عدد مخلوط تبدیل کنیم و سپس، عمل ضرب به روش مساحتی را انجام دهیم. به مثال زیر توجه کنید.
می‌خواهیم اعداد کسری زیر را در هم ضرب کنیم.
برای این کار ابتدا کسرها را به عدد مخلوط تبدیل می‌کنیم. روش‌های گوناگونی برای تبدیل کسر به عدد مخلوط وجود دارد، اما ما در اینجا از روش گسترده‌نویسی استفاده می‌کنیم. خواهیم داشت:
حالا دو عدد مخلوط
را داریم. مراحل ضرب مساحتی این اعداد را به همان روشی که برای اعداد مخلوط بیان کردیم پیش می‌بریم.
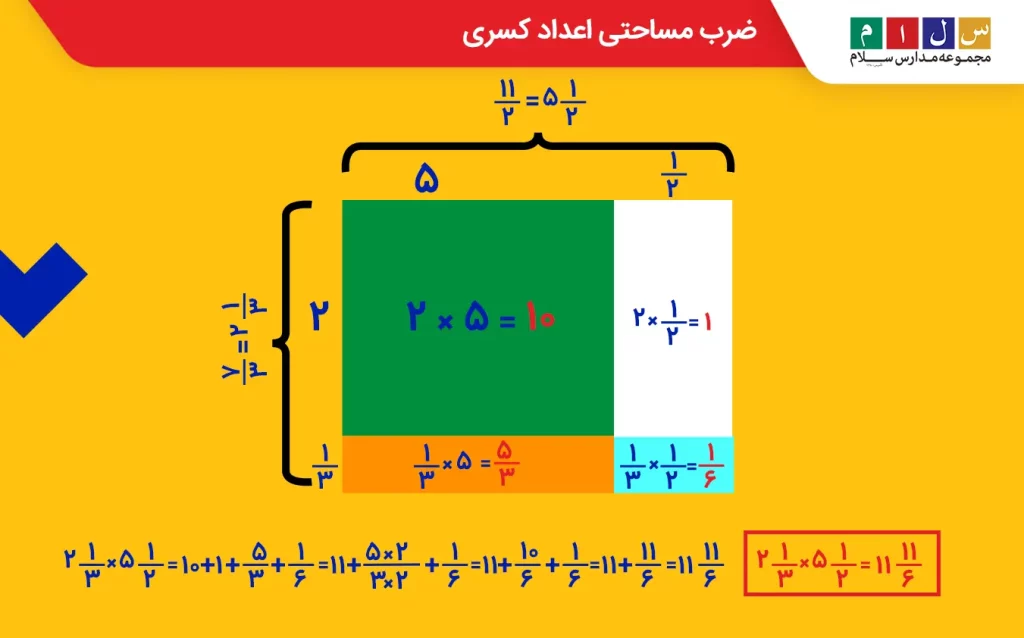
ابتدا یک مستطیل به ابعاد دو عدد مخلوط می‌کشیم و طول و عرض آن را به دو بخش صحیح و کسری اعداد مخلوط قسمت می‌کنیم. چهار مستطیل خواهیم داشت که با محاسبه مساحت هر کدام به‌طور جداگانه و سپس جمع کردن آن‌ها، مساحت مستطیل بزرگ‌تر و درنتیجه حاصل‌ضرب دو عدد به‌دست خواهد آمد.
پیشنهاد مطالعه: آموزش جمع کسرها با مثال
ضرب مساحتی اعداد اعشاری
ضرب مساحتی اعداد اعشاری نیز با روشی مشابه اعداد مخلوط انجام می‌شود. فرض کنید دو عدد اعشاری به‌صورت ۴/۲ و ۳/۵ داریم. برای اینکه حاصل‌ضرب این دو عدد را به روش مساحتی محاسبه کنیم، یک مستطیل به این ابعاد رسم می‌کنیم. سپس، طول و عرض مستطیل را طوری قسمت کرده که بخش صحیح و اعشاری اعداد از هم جدا شود و چهار مستطیل به‌وجود آید.
مساحت مستطیل‌ها را با استفاده از فرمول مساحت مستطیل یعنی طول ضربدر عرض تعیین می‌کنیم و درنهایت، کل مساحت‌ها را با هم جمع می‌زنیم. مجموع مساحت مستطیل‌ها برابر با حاصل‌ضرب ۴/۲ در ۳/۵ خواهد بود.
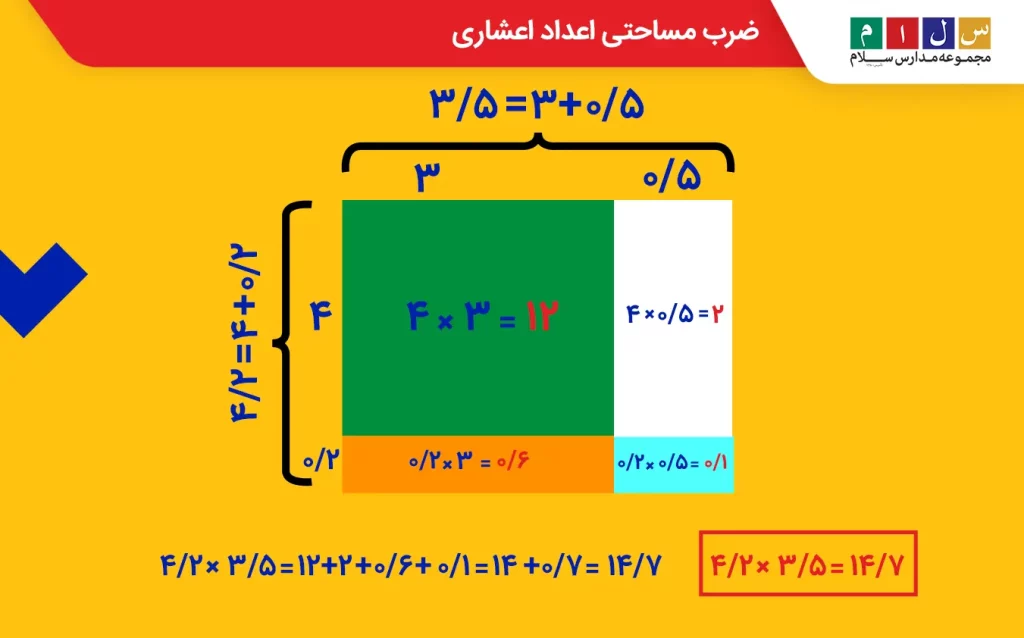
نمونه سؤال ضرب مساحتی با جواب
در این بخش، با حل چند نمونه سؤال همراه با عکس ضرب مساحتی کلاس چهارم، پنجم و ششم را عمیق‌تر یاد می‌گیریم.
نمونه سؤال ضرب مساحتی کلاس چهارم دو رقمی
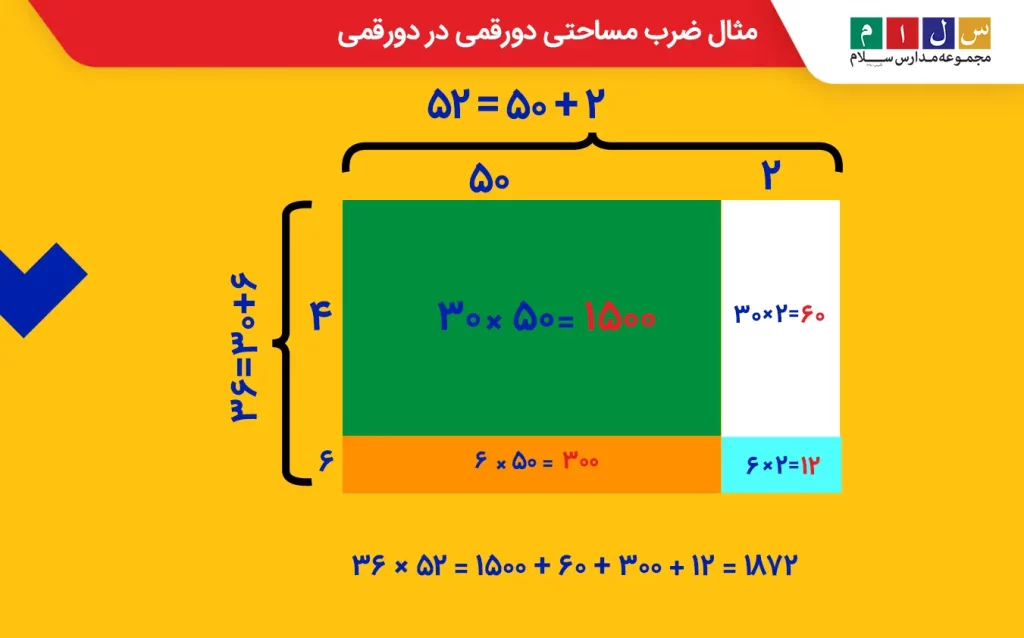
حاصل‌ضرب ۵۲×۳۶ را محاسبه کنید.
جواب: یک مستطیل به ابعاد ۳۶ و ۵۲ می‌کشیم و مانند تصویر زیر طول و عرض آن را به‌گونه‌ای تقسیم می‌کنیم که دهگان و یکان اعداد از هم تفکیک شده و مستطیل بزرگ به مستطیل‌هایی کوچک‌تر با ابعاد مشخص تقسیم‌بندی شود.
با محاسبه مساحت مستطیل‌های کوچک و جمع آن‌ها، حاصل‌ضرب اعداد داده‌شده تعیین خواهد شد.
نمونه سؤال ضرب مساحتی سه رقمی کلاس چهارم
ضرب مساحتی ۲۱ ×۱۲۶ را انجام دهید.
جواب: ضرب داده‌شده ضرب یک عدد سه‌رقمی در دورقمی است. بنابراین، پس از رسم یک مستطیل به‌طول ۱۲۶ و عرض ۲۱، باید طول آن را به سه قسمت و عرض آن را به دو بخش تقسیم کنیم. در نهایت، شش مستطیل خواهیم داشت. توجه داشته باشید که برای درک بهتر بزرگی مساحت مستطیل‌های تقسیم‌شده، تناسب ابعاد آن‌ها را رعایت کنید.
حالا کافی‌ست مساحت مستطیل‌ها را به‌دست آورده و آن‌ها را جمع کنیم تا حاصل ۲۱ × ۱۲۶ تعیین شود.
نمونه سؤال ضرب مساحتی کلاس پنجم
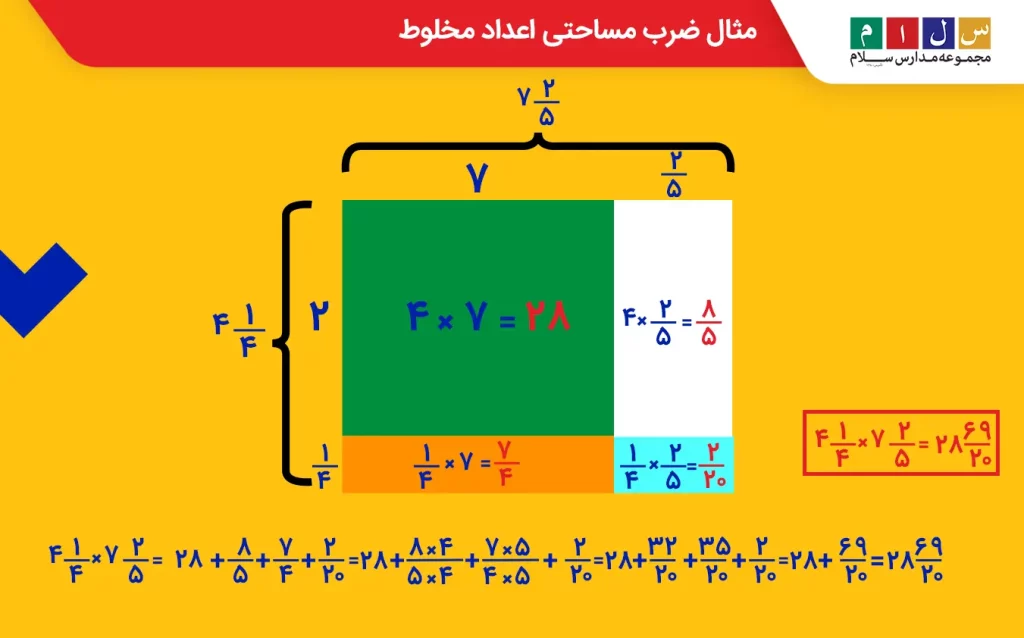
حاصل ضرب اعداد زیر را بدست آورید.
جواب: ابتدا یک مستطیل به ابعاد موردنظر رسم کرده و طول و عرض آن را مانند تصویر زیر به بخش‌های صحیح و کسری اعداد مخلوط تقسیم‌بندی می‌کنیم تا چهار مستطیل با ابعاد و مساحت‌های گوناگون ایجاد شود. اکنون کاری که باید انجام دهیم این است که مساحت مستطیل‌ها را جداگانه حساب کرده و مجموع آن‌ها را به‌دست می‌آوریم. حاصل‌جمع مساحت‌ها مقدار ضرب دو عدد مخلوط را نشان خواهد داد.
نمونه سؤال ضرب مساحتی ششم دبستان
حاصل‌ضرب ۲/۵ × ۶/۷۵ را با روش مساحتی تعیین کنید.
جواب: برای تعیین حاصل‌ضرب این دو عدد اعشاری به روش مساحتی، کافی‌ست یک مستطیل با ابعاد داده‌شده رسم کنید و با جداسازی بخش صحیح و اعشاری اعداد، مستطیل موردنظر را به چهار قسمت تقسیم کنید. پس از تقسیم‌بندی، مساحت مستطیل‌ها را به‌دست آورید و با هم جمع بزنید تا مقدار مساحت مستطیل بزرگ به‌دست آید.
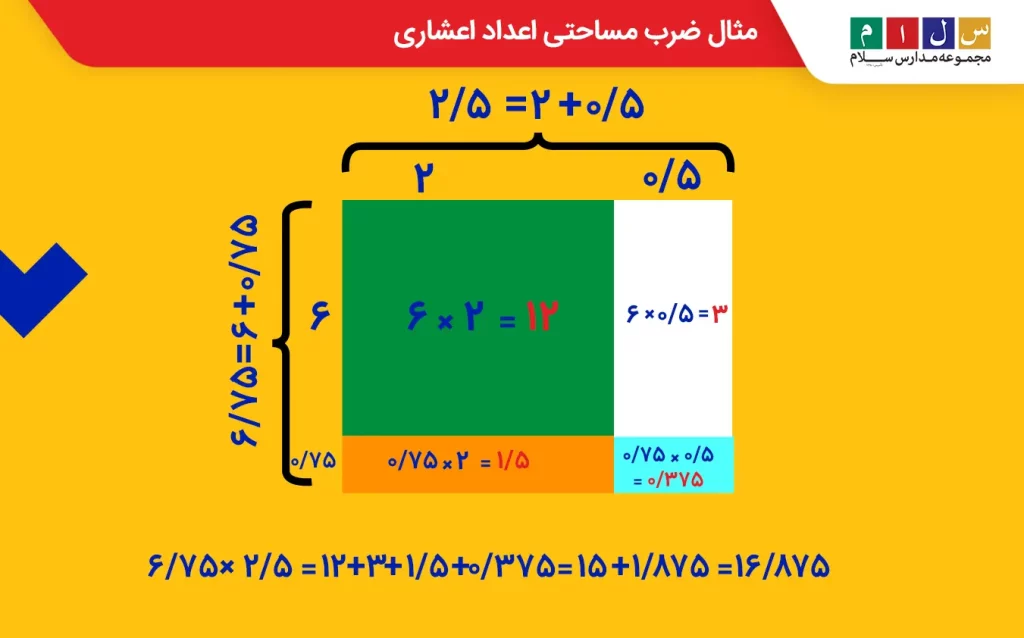
مقدار حاصل، برابر با حاصل‌ضرب اعداد اعشاری یعنی ۲/۵ × ۶/۷۵ خواهد بود.
سخن پایانی
در این مقاله، به آموزش ضرب مساحتی با شکل پرداختیم و همراه با مثال، شیوه انجام آن را توضیح دادیم. ضرب مساحتی روشی ساده برای تعیین حاصل‌ضرب اعداد و درک بهتر عمل ضرب است.
در این روش، باید ابتدا یک مستطیل با ابعاد مشخص رسم کنیم. سپس، با توجه به اعداد داده‌شده، طول و عرض مستطیل را تقسیم کرده و مستطیل‌هایی کوچک‌تر به‌وجود آوریم. پس از تقسیم‌بندی، مساحت تمام مستطیل‌ها را محاسبه کرده و جمع می‌کنیم. مجموع مساحت مستطیل‌ها برابر با مساحت مستطیل بزرگ‌تر و درنتیجه مساوی با حاصل‌ضرب اعداد موردنظر خواهد بود.
3 پاسخ
ممنون از مقاله مفید و کاملتون درباره آموزش ضرب مساحتی کلاس چهارم. من مادر یه دانش‌آموز کلاس چهارم هستم و همیشه دنبال راه‌های ساده‌تر و مؤثرتر برای کمک به فرزندم توی درس‌ها می‌گردم. این روش ضرب مساحتی که توضیح دادید واقعاً ساده و قابل فهم بود و فکر می‌کنم فرزندم خیلی راحت می‌تونه این روش رو یاد بگیره.خیلی خوشحالم که این اطلاعات رو به اشتراک گذاشتید. ممنون از شما
چگونه می‌توان آموزش ضرب مساحتی کلاس چهارم را به دانش‌آموزان داد؟
آموزش ضرب مساحتی کلاس چهارم به این صورت انجام می‌شود که ابتدا هر عدد را به بخش‌های ساده‌تر تقسیم می‌کنیم. برای مثال، وقتی می‌خواهیم ضرب دو عدد دو رقمی مانند ۲۳ و ۴۵ را محاسبه کنیم، آن‌ها را به صورت ۲۰ + ۳ و ۴۰ + ۵ می‌نویسیم و سپس حاصل ضرب هر بخش را به صورت جداگانه محاسبه می‌کنیم. در نهایت، این مقادیر را با هم جمع می‌کنیم تا نتیجه نهایی به دست آید. این روش به دانش‌آموزان کمک می‌کند تا مفهوم ضرب مساحتی کلاس چهارم را بهتر درک کنند.