فهرست مطالب
Toggleدر این مقاله قرار است یکیدیگر از مسائل محیط و مساحت اشکال هندسی بهنام مساحت مثلث متساوی الاضلاع را با جزئیات کامل بررسی کنیم. برای محاسبه مساحت مثلث متساویالاضلاع فرمولهای زیادی وجود دارد. ما ۶ مورد از این فرمولها را با ذکر مثالهای فراوان و متنوع بررسی میکنیم.
نکته! اگر دانشآموز دبستانی هستید یا کودک و دانشآموز دبستانی دارید، تمرکزتان را روی فرمول پایه مساحت مثلث بگذارید و ذهن خود یا دانشآموزتان را درگیر دیگر فرمولها نکنید. با این مقدمه بیایید بهسراغ فرمولهای مساحت مثلث متساویالاضلاع برویم.
مثلث متساوی الاضلاع چیست؟
مثلثها با توجه به اندازه ضلعهایشان به ۳ دسته تقسیم میشوند:
- مثلث مختلفالاضلاع (دارای ۳ ضلع نامساوی)
- مثلث متساویالساقین (دارای ۲ ضلع مساوی)
- مثلث متساویالاضلاع (دارای ۳ ضلع مساوی)
ما در این مقاله قرار است تنها درباره مساحت مثلث متساویالاضلاع صحبت کنیم. این مثلث ۲ ویژگی بسیار مهم دارد که در تعیین مساحتش به ما کمک میکند:
- هر ۳ ضلع مثلث متساویالاضلاع با یکدیگر برابرند، پس برای محاسبه مساحتش کافیست اندازه یکی از ضلعهای آن را داشته باشیم.
- ۳ زاویه مثلث متساویالاضلاع با هم مساویاند. باتوجه به اینکه جمع زوایای داخلی مثلث ۱۸۰ درجه است، پس هر کدام از زوایای مثلث متساویالاضلاع ۶۰ درجه دارند.
سایر ویژگی های مثلث متساوی الاضلاع عبارتند از:
- مثلث متساوی الاضلاع یک مرکز تقارن دارد
- مثلث متساوی الاضلاع دارای سه خط تقارن است
- ارتفاعها با هم و نیمسازهای داخلی با هم برابرند.
ارتفاع، میانه و نیمساز و عمود منصف نظیر هر ضلع آن بر هم منطبق اند.

اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
تعریف مساحت مثلث متساوی الاضلاع
فضا یا سطح درونی یک مثلث متساوی الاضلاع را مساحت آن میگویند. ما در مقاله مساحت چیست، مفصل درباره تعریف مفهومی مساحت صحبت کردهایم. تعداد واحدهای مربعی که درون یک مثلث متساویالاضلاع جا میگیرند، مساوی با مساحت آن مثلث است. به مثال زیر دقت کنید:
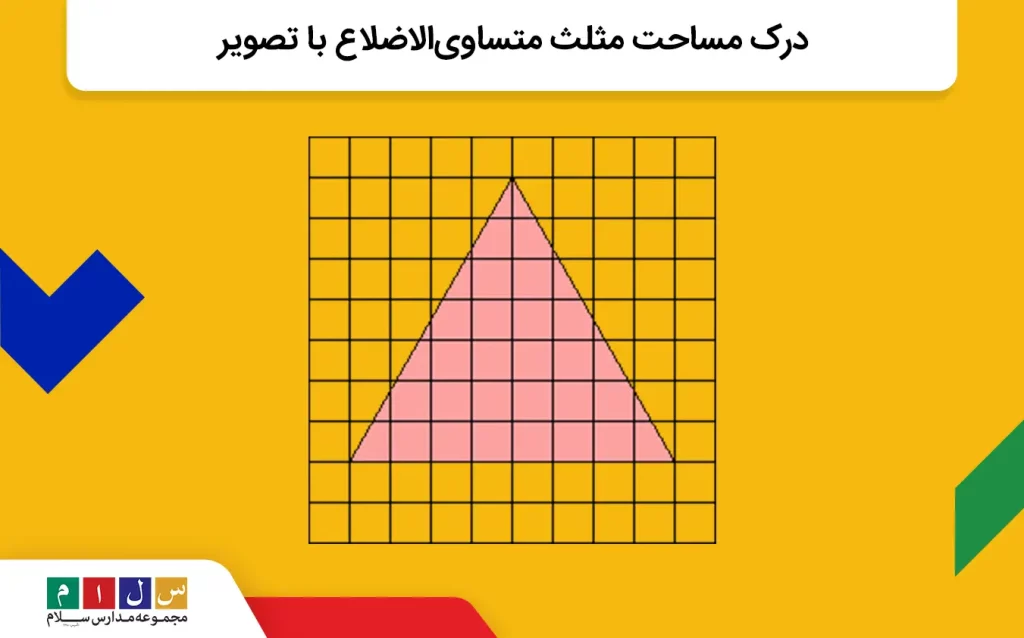
تعداد واحدهای مربع کوچکی که سطح داخلی مثلث بالا را پوشاندهاند، مساحت آن مثلث را نشان میدهند. همانطور که میبینید، فضای اِشغالشده توسط مثلث متساوی الاضلاع، دارای تعدادی مربع کامل و تعدادی مربع نیمهکامل است. این مسئله محاسبه مساحت مثلث بدون استفاده از فرمول را دشوار میکند.
پیشنهاد مطالعه: مساحت متوازی الاضلاع
۶ فرمول مساحت مثلث متساوی الاضلاع
از فرمولهای زیادی برای محاسبه مساحت متساویالاضلاع استفاده میشود که در ادامه به مهمترین آنها اشاره میکنیم:
- فرمول پایه مساحت مثلث (A=h×b÷۲) (نکته مهم: در پایه ابتدایی فقط همین فرمول را با دانشآموزان کار میکنند)
- فرمول اختصاصی مساحت مثلث متساویالاضلاع A= (√۳ ÷ ۴) × a²
- استفاده از مثلثات و اندازه ۲ ضلع و زاویه بین آنها؛ (A = ۱ ÷ ۲ab × sin C )
- فرمول هرون (A= √s (s – a) × (s – b) × (s – c))
- محاسبه مساحت مثلث متساویالاضلاع با ارتفاع (A= (√۳ ÷ ۳) × h²)
- فرمول مساحت مثلث متساویالاضلاع با محیط (A= √۳ × P² ÷ ۳۶)
بیایید هرکدام از این فرمولها را در مثال ببینیم.
فرمول پایه مساحت مثلث
این فرمول برای همه انواع مثلثها کاربرد دارد و در پایه چهارم دبستان به دانشآموزان آموزش داده میشود. برای محاسبه مساحت مثلث متساوی الاضلاع با این فرمول، به اطلاعات زیر نیاز داریم:
- اندازه ارتفاع مثلث
- اندازه قاعده مثلث
همانطور که در قسمت قبل دیدیم، فرمول پایه مساحت مثلث به این شرح است:
۲ ÷ قاعده × ارتفاع = مساحت مثلث متساویالاضلاع
یا
A= h × b ÷ 2
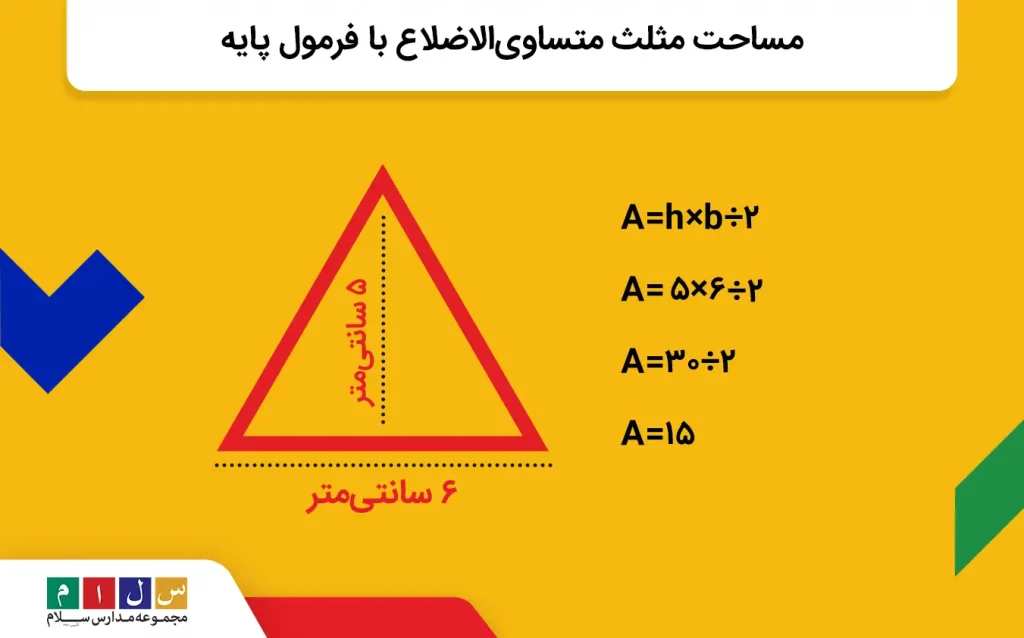
مثال: اگر قاعده و ارتفاع یک مثلث متساوی الاضلاع بهترتیب ۵ و ۶ سانتیمتر باشد، مساحت این مثلث چقدر میشود؟
جواب: چون اندازه ارتفاع و قاعده مثلث متساویالاضلاع را داریم، از فرمول اصلی و ساده مساحت مثلث برای رسیدن به جواب استفاده میکنیم:
فرمول اختصاصی مساحت مثلث متساوی الاضلاع
برای محاسبه مساحت مثلث متساوی الاضلاع یک فرمول ویژه هم وجود دارد. این فرمول مختص به این نوع مثلث است و برای استفاده از آن فقط کافیست اندازه یکی از ضلعها را داشته باشیم.
A= √۳ ÷ ۴ × a²
اندازه یکضلع بهتوان ۲ × ۴ ÷ جذر ۳ = مساحت مثلث متساویالاضلاع
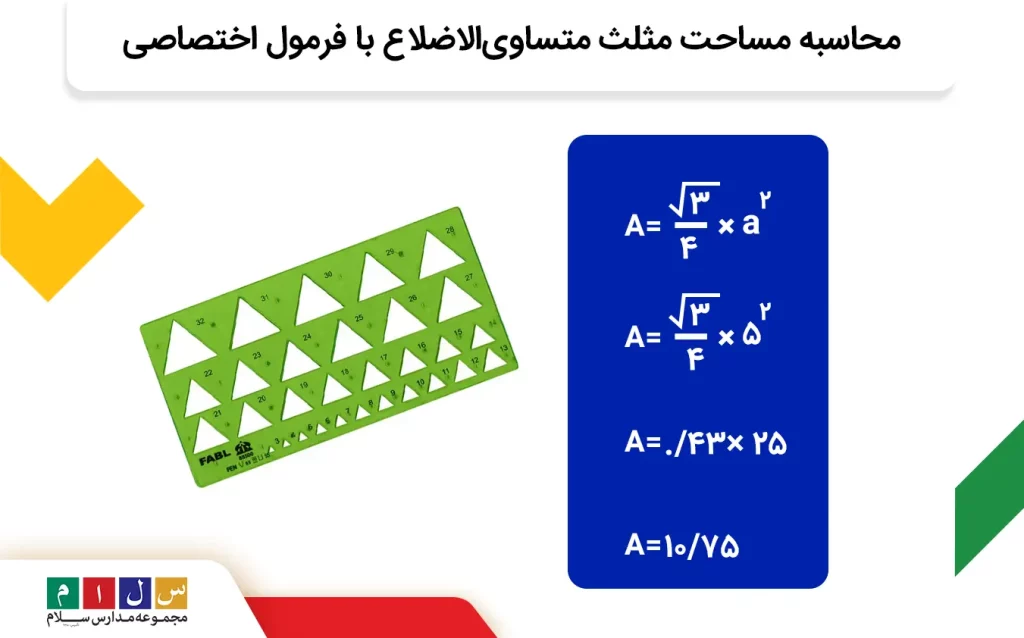
مثال: یک شابلون مثلثیشکل با ۳ ضلع مساوی داریم. اگر اندازه یکی از ضلعهای این شابلون ۵ سانتیمتر باشد، مساحت آن چقدر میشود؟
جواب: باتوجه به اینکه اندازه ۳ ضلع مثلث با یکدیگر برابرند، یعنی با یک مثلث متساویالاضلاع مواجهایم. در صورت سوال اندازه یکی از ضلعها داده شده است، پس میتوانیم از فرمول اختصاصی مساحت مثلث متساویالاضلاع استفاده کنیم.
فرمول مساحت مثلث متساوی الاضلاع با ۲ ضلع و زاویه بین
اگر اندازه ۲ ضلع و زاویه بین آنها را داشته باشیم، برای محاسبه مساحت مثلث میتوانیم از فرمول زیر استفاده کنیم. بهصورت کلی ۳ حالت برای محاسبه مساحت مثلث از طریق این فرمول وجود دارد که هر سه با هم برابرند؛ یعنی:
A = (۱ ÷ ۲) × (ab × sinC) = (۱ ÷ ۲) (bc × sinA) = (۱ ÷ ۲ ) × (ac × sinB)
شکل سادهشده فرمول بالا به این صورت است:
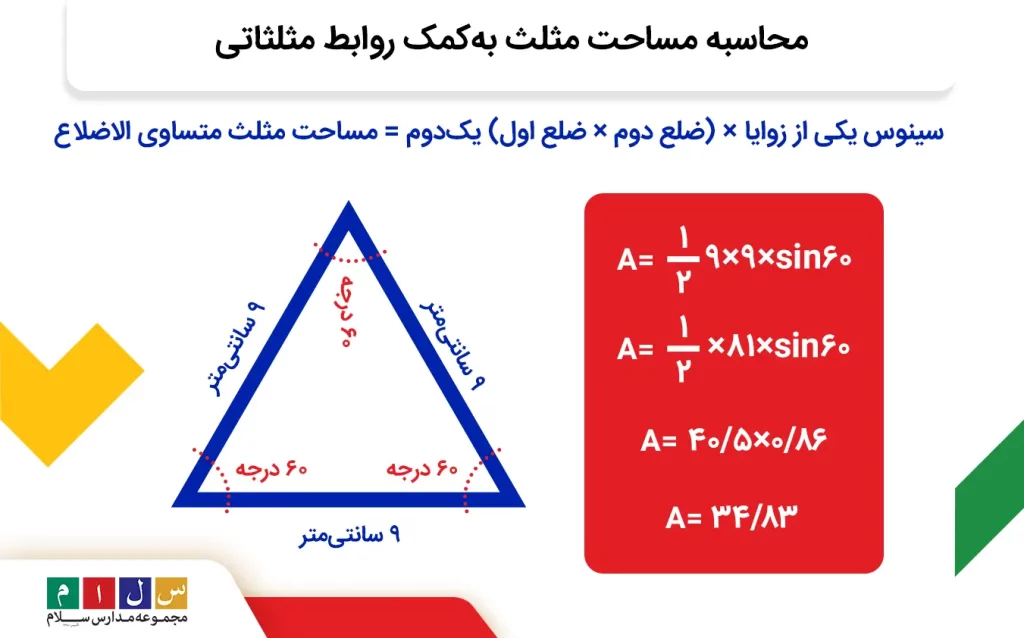
سینوس یکی از زوایا × (ضلع دوم × ضلع اول) یکدوم = مساحت مثلث متساوی الاضلاع
مثال: میخواهیم مساحت یک تابلوی راهنمایی مثلثیشکل با ۳ ضلع مساوی را حساب کنیم. اگر اندازه یکی از ضلعهای این تابلو ۹ سانتیمتر باشد، مساحت آن را حساب کنید.
جواب: چون ۳ ضلع تابلوی راهنمایی با یکدیگر برابرند، پس مثلث متساوی الاضلاع است. اگر بخواهیم مساحت این مثلث را به روش مثلثاتی (۲ ضلع و زاویه بین) حل کنیم، حداقل به اندازه ۲ ضلع و زاویه بین آنها نیاز داریم، اما در صورت سوال فقط اندازه یکضلع را به ما دادهاند. اینجاست که آگاهی از ۲ ویژگی اصلی مثلث متساویالاضلاع به کارمان میآید:
- هر ۳ ضلع مثلث با هم برابرند. پس اگر اندازه یکی از ضلعها ۹ سانتیمتر است، اندازه دیگر ضلعها هم همین مقدار است.
- ۳ زاویه مثلث با هم مساوی و برابر با ۶۰ درجه هستند. پس مسلما اندازه زاویه بین ۲ ضلع مساویست با ۶۰ درجه.
حالا که اطلاعات لازم برای استفاده از این فرمول را به دست آوردیم، بیایید مساحت تابلوی راهنمایی را حساب کنیم:
محاسبه مساحت مثلث متساویالاضلاع به کمک فرمول هرون
یکیدیگر از فرمولهای ساده و پرکاربرد برای محاسبه مساحت مثلث، فرمول هرون است. برای استفاده از این فرمول به اندازه ۳ ضلع مثلث نیاز داریم. باتوجه به اینکه مثلث متساوی الاضلاع ۳ ضلع مساوی دارد، پس داشتن اندازه یکی از ضلعها هم کافیست. فرمول هرون به این ترتیب است:
A= √(s (s – a) × (s – b) × (s – c))
- نصف محیط مثلث s= (a + b + c) ÷ ۲
- a، b و c = اندازه ۳ ضلع مثلث
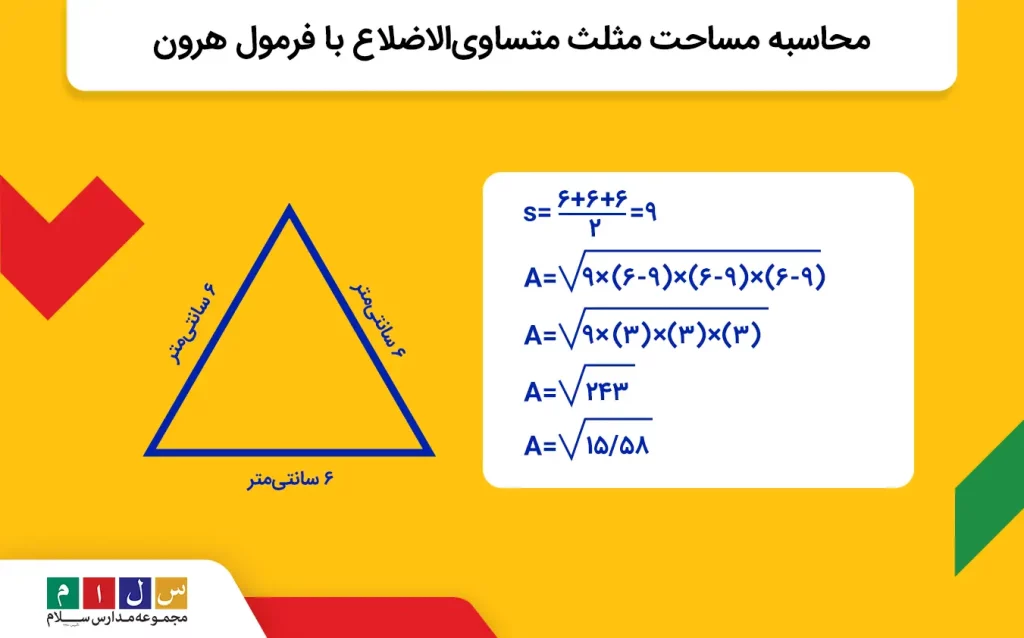
مثال: ساعت دیواری مثلثیشکلی با ضلع مساوی داریم که میخواهیم مساحتش را حساب کنیم. اگر اندازه یکضلع این مثلث ۶ سانتیمتر باشد، مساحت آن را به کمک فرمول هرون محاسبه کنید:
جواب: ۳ ضلع مثلث متساویالاضلاع با یکدیگر برابرند، پس اندازه ۳ ضلع این مثلث برابر با ۶ سانتیمتر است.
فرمول مساحت مثلث متساویالاضلاع با ارتفاع
اگر ارتفاع مثلث متساویالاضلاع را داشته باشیم، بااستفاده از فرمول زیر میتوانیم مساحت آن را حساب کنیم:
(A= √۳ ÷ ۳ × h²)
- h = ارتفاع
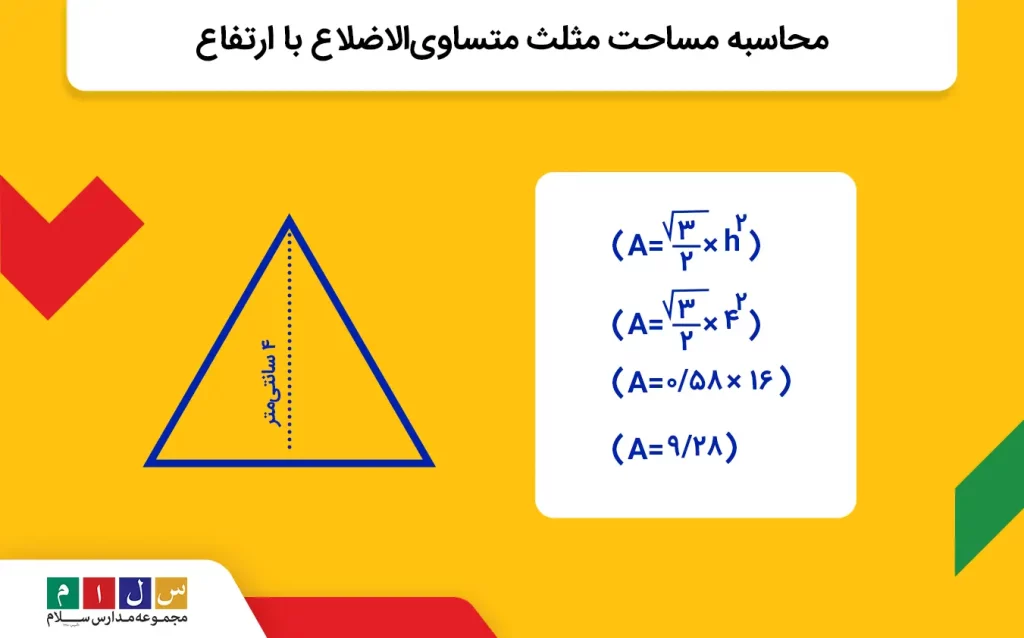
مثال: اگر ارتفاع یک مثلث متساویالاضلاع ۴ سانتیمتر باشد، مساحت آن چقدر میشود؟
جواب: باتوجه به اینکه اندازه ارتفاع را داریم، میتوانیم از فرمول محاسبه مساحت مثلث متساویالاضلاع با ارتفاع استفاده کنیم.
فرمول مساحت مثلث متساویالاضلاع با محیط
برای محاسبه مساحت مثلث متساویالاضلاع بهکمک محیط مثلث متساوی الاضلاع، طبق فرمول زیر عمل میکنیم:
(A= √۳ × (P² ÷ ۳۶))
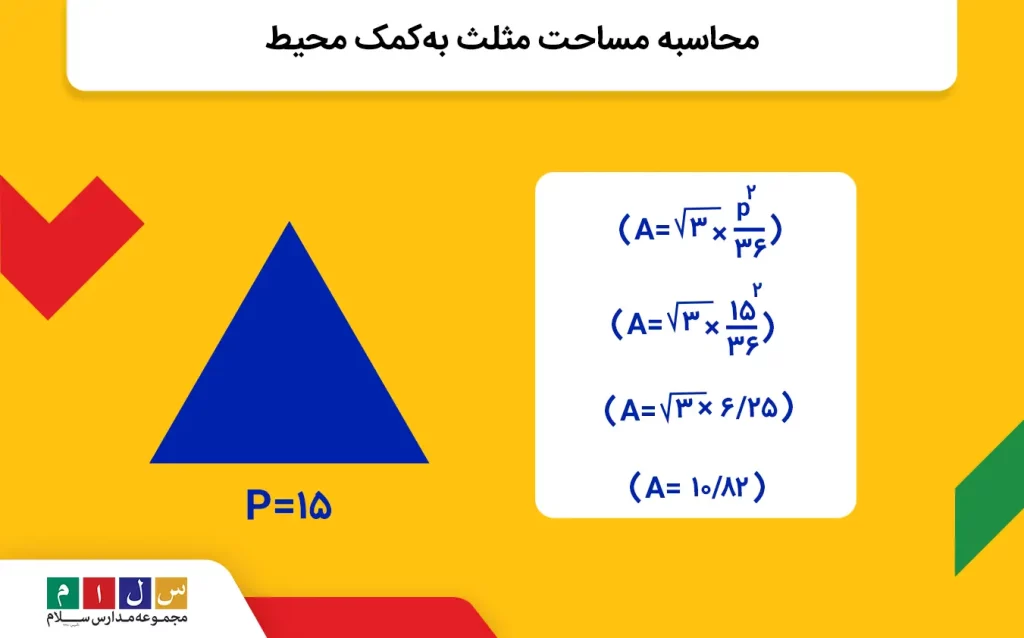
مثال: محیط یک مثلث متساوی الاضلاع ۱۵سانتیمتر است. مساحت این مثلث را حساب کنید:
مثال برای محاسبه مساحت مثلث متساوی الاضلاع
یادگیری مسائل ریاضی و هندسی بدون مثال و حل تمرین ممکن نیست. پس حتما زیاد و متنوع مثال ببینید و حل کنید تا دستتان راه بیفتد. اگر به حل مثال علاقه دارید، از همینجا شروع کنید.
مثال: علی میخواهد یک شلف دیواری به شکل مثلث متساوی الاضلاع برای خانهاش خریداری کند. اگر اندازه یکی از ضلعهای این شلف دیواری ۲ متر باشد، به علی کمک کنید تا مساحت آن را حساب کند.
جواب: نکته جالب اینکه برای پاسخگویی به این سوال میتوان از فرمولهای مساحت متوازی الاضلاع کلاس ششم استفاده کرد. پس بیایید از همه این فرمولها به سوال پاسخ دهیم و سپس جوابها را با هم مقایسه کنیم.
حل مثال با استفاده از فرمول پایه مساحت مثلث
برای پاسخگویی بهکمک این فرمول به قاعده و ارتفاع مثلث نیاز داریم. در صورت سوال، اندازه یک ضلع مثلث آمده است که چون ۳ ضلع مثلث متساویالاضلاع برابرند، میتوانیم آن را بهعنوان قاعده در نظر بگیریم. برای محاسبه ارتفاع مثلث متساویالاضلاع هم از فرمول زیر استفاده میکنیم:
- h = ارتفاع مثلث
- a = اندازه یک ضلع مثلث متساویالاضلاع
پس برای محاسبه ارتفاع مثلث متساویالاضلاع خواهیم داشت:
h= (√۳ ÷ ۲) × ۲
h= √۳= ۱/۷۳
حالا که اندازه ارتفاع را به دست آوردیم، میتوانیم از فرمول پایه مساحت مثلث استفاده کنیم:
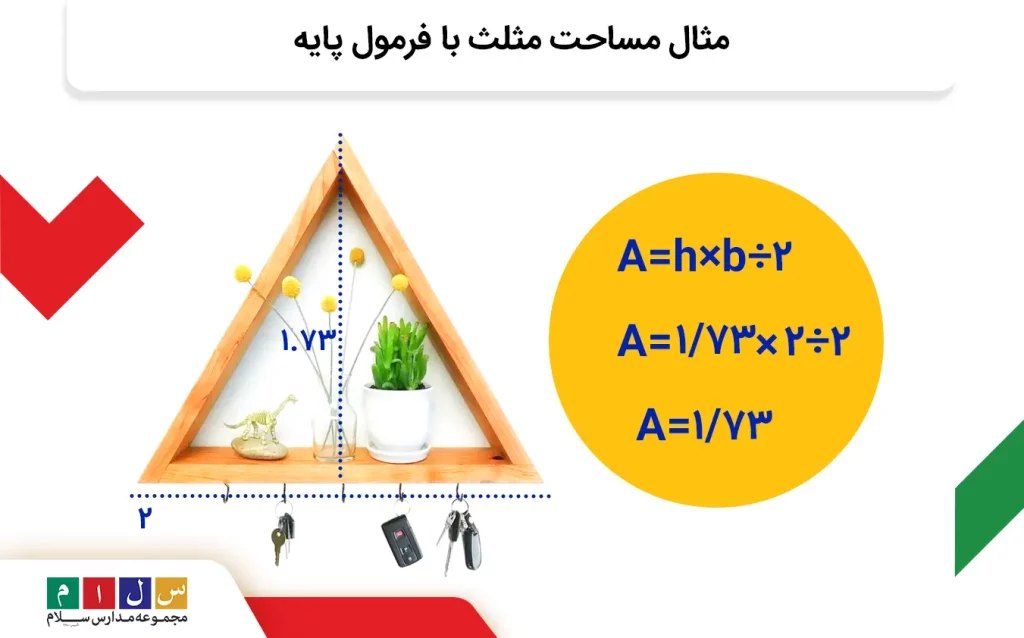
حل مثال با کمک فرمول اختصاصی مساحت مثلث متساوی الاضلاع
برای استفاده از این فرمول فقط به اندازه یکضلع نیاز داریم که در صورت سوال به ما داده شده است.
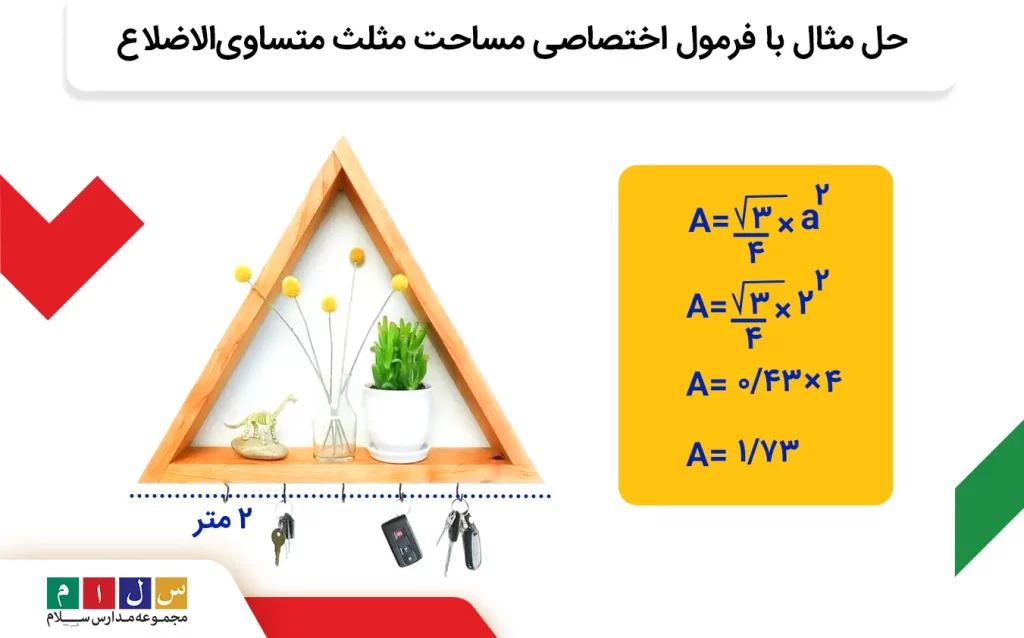
همانطور که میبینید، چه مساحت مثلث را با فرمول پایه و چه اختصاصی محاسبه کنیم، نتیجه بهدستآمده یکسان است.
حل مثال مساحت مثلث متساوی الاضلاع با ۲ ضلع و زاویه بین
چون با مثلث متساویالاضلاع طرفایم، ۳ ضلع مساوی و ۳ زاویه ۶۰ درجه داریم. پس برای محاسبه مساحت این شلف دیواری با فرمول ۲ ضلع و زاویه بین خواهیم داشت:
سینوس یکی از زوایا × (ضلع دوم × ضلع اول) یکدوم = مساحت مثلث متساوی الاضلاع
A= (۱ ÷ ۲) × ۲ × ۲ × sin۶۰
A= ۲ × ۰/۸۶۶
A= ۱/۷۳
نکته: باز هم مساحت مثلث با مقدار بهدستآمده توسط فرمولهای قبلی برابر است.
حل مثال به کمک فرمول هرون
برای استفاده از فرمول هرون باید اندازه ۳ ضلع مثلث را داشته باشیم. بهدلیل اینکه همه اضلاع مثلث متساویالاضلاع با یکدیگر برابرند، پس داشتن یکی از آنها بهمعنای داشتن اندازه هر ۳ مورد آنهاست. در فرمول هرون ابتدا باید نصف مساحت مثلث را حساب کنیم:
s= (a + b +c) ÷ ۲
s = (۲ + ۲ + ۲) ÷ ۲ = ۳
حالا که اندازه s را به دست آوردیم، میتوانیم آن را در فرمول هرون جایگذاری کنیم و به جواب برسیم.
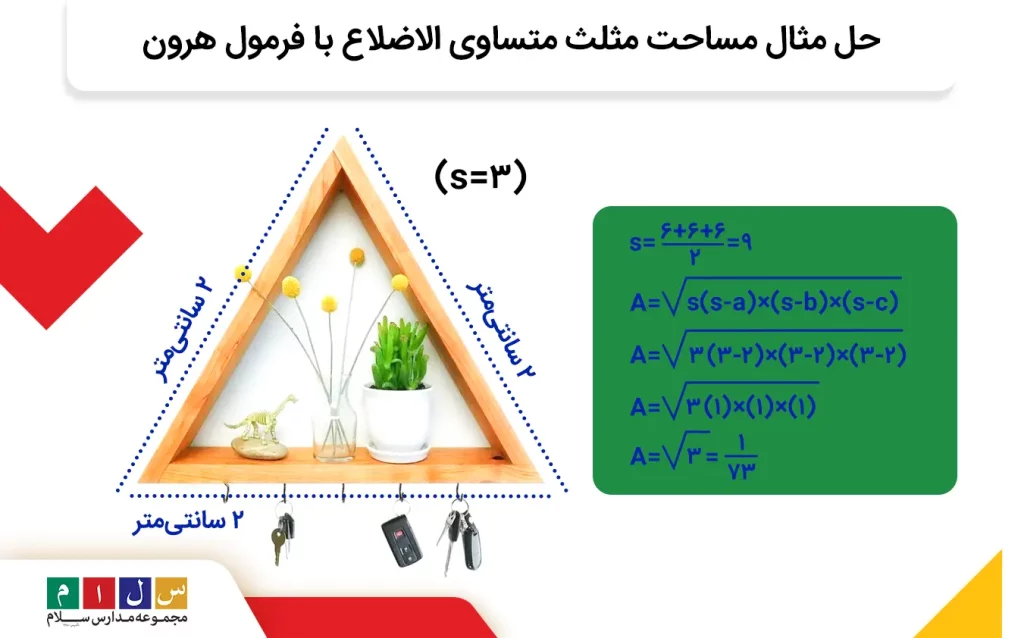
با فرمول هرون هم مساحت شلف مثلثی را حساب کردیم و باز هم مقدار بهدستآمده مشابه نتیجه فرمولهای قبلیست.
حل مثال مساحت مثلث متساویالاضلاع با ارتفاع
ارتفاع این مثلث را بالاتر و در قسمت فرمول پایه به دست آوردیم. اگر این مقدار را در فرمول زیر قرار دهیم، میتوانیم مساحت مثلث را فقط با ارتفاع حساب کنیم:
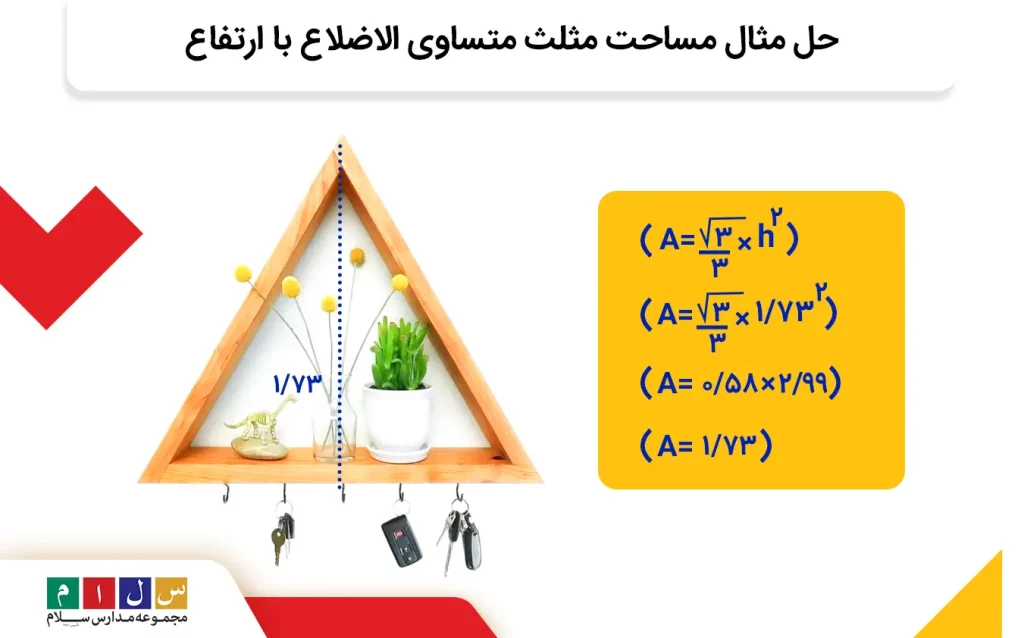
نتیجه فرمول مساحت متساویالاضلاع با ارتفاع هم با نتایج دیگر فرمولها برابر است.
حل مثال مساحت مثلث متساویالاضلاع با محیط
چون اندازه ۳ ضلع مثلث را داریم، بهراحتی میتوانیم محیط آن را حساب کنیم:
p= ۲ + ۲ + ۲ = ۶
حالا که اندازه محیط مثلث را به دست آوردیم، مساحت مثلث را بهکمک فرمول زیر محاسبه میکنیم:
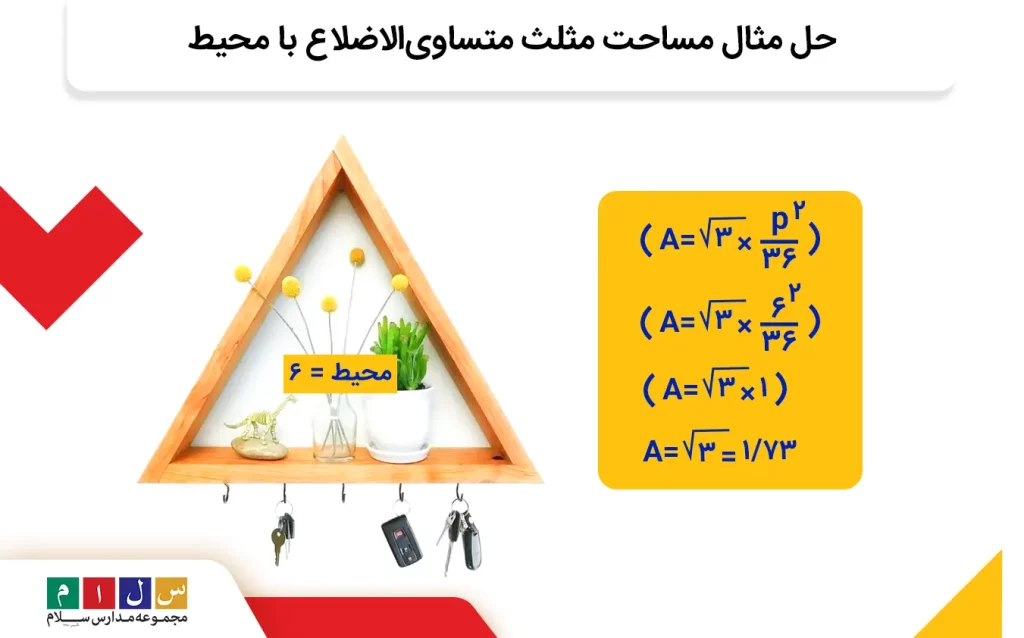
ما در مقاله مساحت مثلث، تمامی فرمول های مساحت مثلث را از ساده تا سخت به طور کامل بررسی کردیم، پس حتما برای بررسی دقیق تر به این مقاله سر بزنید.
سخن پایانی
مثلث متساویالاضلاع یک ۳ ضلعی منتظم است که برای محاسبه مساحتش فقط کافیست اندازه یک ضلع آن را داشته باشیم. با همین ضلع میتوانیم مساحت مثلث متساویالاضلاع را بهکمک فرمولهای مختلف حساب کنیم و ارتفاعش را به دست آوریم. فرقی ندارد از کدام روش و فرمول برای رسیدن به مساحت استفاده میکنید، زیرا همه آنها در نهایت به یک جواب میرسند.
اگر فرزند یا دانشآموز ابتدایی دارید، حواستان باشد که دانشآموزان دبستانی فقط با فرمول پایه مساحت مثلث متساویالاضلاع، یعنی «ارتفاع ضربدر قاعده تقسیم بر ۲» کار میکنند. پس ذهنشان را با فرمولهای دیگر پر نکنید تا بهمرور و در مقاطع بالاتر با آنها آشنا شوند.
سوالات متداول
- منظور از مساحت مثلث متساوی الاضلاع چیست؟
فضای داخلی تحت پوشش توسط یک مثلث متساویالاضلاع را مساحت مثلث متساوی الاضلاع میگویند. مساحت را بسته به موقعیت با میلیمتر مربع، سانتیمتر مربع، متر مربع، هکتار و کیلومتر مربع اندازهگیری میکنند. - فرمول مساحت مثلث متساویالاضلاع چیست؟
مساحت مثلث متساویالاضلاع را با فرمولهای زیادی میتوان محاسبه کرد که ۶ مورد از آنها را در متن مقاله با مثالهای فراوان توضیح دادهایم. فرمول اختصاصی مساحت مثلث متساویالاضلاع عبارت است از «جذر ۳ تقسیم بر ۴ ضربدر اندازه یک ضلع بهتوان ۲». - مساحت مثلث متساویالاضلاع کلاس سوم چیست؟
دانشآموزان دبستانی در پایه سوم فقط با مساحت مثلث آشنا میشوند. فرمول و نحوه محاسبه مساحت انواع مثلثها از جمله متساویالاضلاع در پایه چهارم دبستان به کودکان آموزش داده میشود. دانشآموزان دبستانی فقط با فرمول پایه مساحت مثلث یعنی «ارتفاع ضربدر قاعده تقسیم بر ۲» کار میکنند که در متن مقاله این فرمول را با مثال توضیح دادهایم.










24 پاسخ
سلام، مقاله شما در مورد مساحت مثلثهای متساویالاضلاع خیلی مفید بود! اما میخواستم بدونم که برای محاسبه مساحت متوازی الاضلاع کلاس ششم چه فرمولی رو باید استفاده کنم، مخصوصاً وقتی که ارتفاع مثلث رو داشته باشم؟
سلام، مقاله شما در مورد مساحت مثلث متساویالاضلاع واقعاً به من کمک کرد. با این حال، من هنوز یک سوال دارم: وقتی در مورد مساحت مثلث متوازی الاضلاع صحبت میکنیم، چطور میتوانیم از فرمولهای مشابه برای محاسبه مساحت مثلثهای دیگر که ارتفاع آنها متفاوت است استفاده کنیم؟ بهخصوص وقتی که در کنار این مساحت نیاز داریم از ویژگیهای هندسی دیگه مثل زاویهها یا طول اضلاع استفاده کنیم، چه فرمولهایی کاربرد دارند؟
یه سوال داشتم بهترین راه یادگیری مساحت مثلث متساوی الاضلاع چیه؟
با سلام وقت بخیر تمرین همراه با درک مفهومی، بهترین مسیر برای ماندگاری در ذهن است.
دمتون گرم، مساحت مثلث متساوی الاضلاع رو بالاخره فهمیدم
چرا یاد گرفتن مساحت مثلث متساوی الاضلاع انقدر مهمه؟
این مبحث برای چه پایهای مهمتره؟
چرا همه ضلعها برابر باشن، مساحت فرق میکنه؟
مساحت مثلث متساوی الاضلاع چه فرقی با بقیه مثلثها داره؟
مساحت مثلث متساوی الاضلاع به چه چیزایی بستگی داره؟
واقعاً ساده و قابل فهم گفتین، ممنون
این مساحت مثلث متساوی الاضلاع دقیقاً به چی اشاره میکنه؟
سلام خیلی ممنونم برای توضیح دقیقو با شکلتون
این مساحت مثلث متساوی الاضلاع تو زندگی واقعی هم هست؟
خسته نباشید، توضیح مساحت مثلث متساوی الاضلاع عالی بود
ممنون از این مقاله، توضیح مساحت مثلث متساوی الاضلاع عالی بود
اگه فقط طول ضلع مثلث متساویالاضلاع رو داشته باشیم، میشه مساحتشو حساب کرد؟
میشه مساحت مثلث متساویالاضلاع رو بدون ارتفاع حساب کرد؟
با سلام وقت بخیر اگه فرمول یادمون بره، راه دیگهای هست؟
اگه طول ضلع رو اشتباه بذاریم، مساحت خیلی فرق میکنه؟
واقعاً توضیحات مساحت مثلث متساوی الاضلاع خیلی خوب بود، ممنون
با سلام وقت بخیر از همراهی و نظر مثبت شما سپاسگزارم.
مرسی از مثالها و توضیحاتتون
سلام وقتتون از همراهی و نظر مثبت شما سپاسگزاریم.