فهرست مطالب
Toggleکسرها نشاندهنده بخشی از یک کل هستند و از دو بخش صورت و مخرج تشکیل شدهاند. جمع کردن این اعداد با جمع معمولی اعداد صحیح اندکی متفاوت است زیرا کسرها دارای صورت و مخرج هستند. اگر میخواهید با روش جمع کسرها آشنا شوید، پیشنهاد میکنیم این آموزش را دنبال کنید تا هم نحوه جمع کردن اعداد کسری را بیاموزید و هم نحوه استفاده از شکل و محور برای تعیین حاصلجمع این اعداد را فراگیرید.
جمع کسرها با مخرج مساوی
کسرها انواع مختلفی دارند و لازم است هنگام جمع کردن آنها بررسی کنیم که آیا مخرجشان مساوی است یا خیر. اگر مخرج کسرهایی که با هم جمع میشوند، یکسان باشد، عمل جمع بسیار راحت خواهد بود. کافیست مخرج کسر را ثابت و بدون تغییر نگه دارید و تنها صورتها را با هم جمع کنید. بهعنوان مثال، حاصلجمع کسرهای بهصورت زیر محاسبه میشود:
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
جمع کسرها با مخرج نامساوی
وقتی مخرج کسرهایی که میخواهیم آنها را با هم جمع کنیم، نامساوی باشند، اولین کاری که باید انجام دهیم یکسان کردن مخرجها با مخرج مشترک گرفتن است. برای مخرج مشترک گرفتن باید ابتدا ک م م (کوچکترین مضرب مشترک) مخرجها را بیابیم. در ادامه، با یک مثال مراحل جمع کردن اینگونه کسرها را توضیح میدهیم.
مثال: حاصلجمع را بهدست آورید.
همانطور که میبینید، مخرج دو کسر نامساوی است. پس باید ابتدا با پیدا کردن کوچکترین مضرب مشترک ۲ و ۷ مخرج کسرها را برابر کنیم. منظور از کوچکترین مضرب مشترک ۲ و ۷، کوچکترین عددی است که هم بر ۲ و هم بر ۷ بخشپذیر است.
بیایید با هم مضربهای ۲ و ۷ را بررسی کنیم و ببینیم کوچکترین مضرب مشترک بین آنها کدام است.
- مضربهای ۲: ۲، ۴، ۶، ۸، ۱۰، ۱۲، ۱۴، ۱۶ و غیره.
- مضربهای ۷: ۷، ۱۴، ۲۱، ۲۸ و غیره.
همانطور که مشاهده میکنید، عدد ۱۴ کوچکترین و اولین مضرب مشترک عدد ۲ و ۷ است. بنابراین، باید کاری کنیم که مخرج هر دو کسر برابر با ۱۴ شود. برای این کار باید با قانون ضرب کسر ها آشنا باشیم و کافیست صورت و مخرج کسر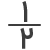
را در ۲ ضرب کنیم.
نکته: اگر صورت و مخرج کسر در یک عدد ضرب شوند، کسر حاصل مساوی با کسر اولیه خواهد بود و تغییری در مقدار آن ایجاد نمیشود. بنابراین، زمانی که میخواهیم مخرج کسر را در یک عدد ضرب کنیم، باید صورت آن را نیز در همان عدد ضرب کنیم تا مقدار کسر تغییر نکند.
با توجه به توضیحات دادهشده، خواهیم داشت:
کسر حاصل یک کسر بزرگتر از واحد است و میتوانیم آن را به یک عدد مخلوط تبدیل کنیم:
به یاد داشته باشید که برای مخرج مشترک گرفتن لازم نیست تمام کسرها را در یک عدد موردنظر ضرب کنیم. گاهی اوقات ممکن است تنها یکی از مخرجها نیاز به تغییر داشته باشند. به مثال زیر توجه کنید.
میخواهیم حاصل عبارت را بهدست آوریم. میبینیم که مخرج این دو کسر یکسان نیست. پس باید ابتدا با پیدا کردن کوچکترین مضرب مشترک ۳ و ۱۵، مخرجها را مساوی کنیم و سپس، کسرها را با هم جمع بزنیم.
- مضربهای ۱۵: ۱۵ ۳۰ و غیره.
- مضربهای ۳: ۳، ۶، ۹، ۱۵ و غیره.
با توجه به مضربهای ۳ و ۱۵، میتوان گفت کوچکترین مضرب مشترک این دو عدد ۱۵ است. پس مخرج مشترک دو کسر را باید برابر با 15 قرار دهیم؛ یعنی آنها را در عددی ضرب کنیم که مخرجشان ۱۵ شود. خواهیم داشت:
همانطور که دیدید، مخرج یکی از کسرها ۱۵ است و دیگر نیازی به تغییر آن نیست.
جمع کسرها با شکل
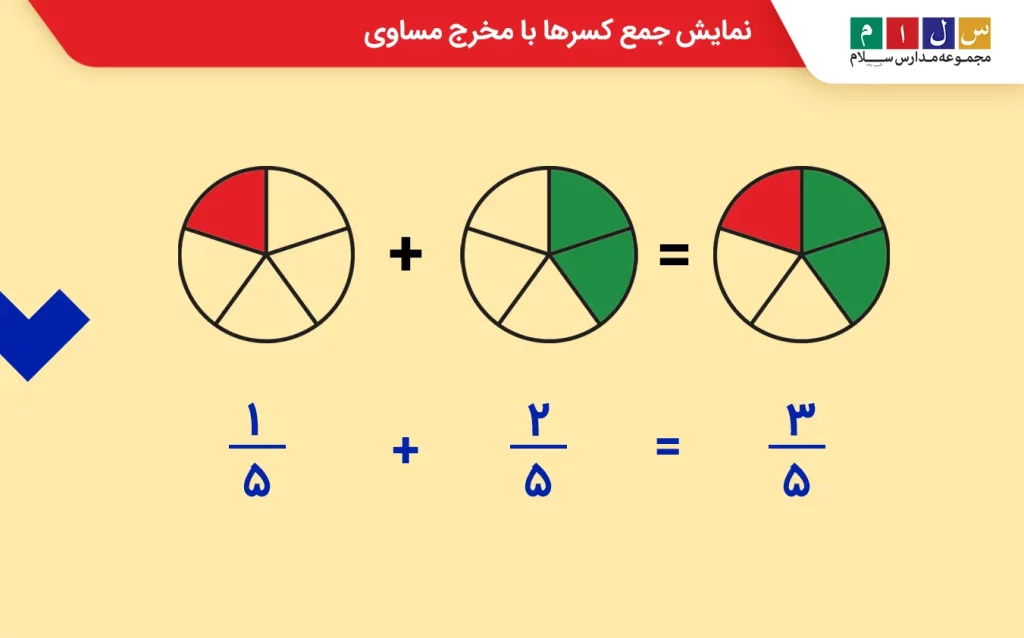
در این بخش، جمع کردن کسرها را با رسم شکل نشان میدهیم. ابتدا برای حالتی که مخرج کسرها مساوی است، یک مثال حل میکنیم. فرض کنید میخواهیم حاصلجمع عبارت زیر را تعیین کنیم:
در این عبارت، مخرج هر دو کسر با هم برابر و مساوی با ۵ است. بنابراین، ابتدا مانند تصویر زیر برای هر کدام از کسرها یک شکل دلخواه مثل دایره یا مستطیل رسم کرده و هر کدام را به ۵ قسمت مساوی تقسیم میکنیم. برای نمایش کسر اول یعنی باید ۱ قسمت از ۵ قسمت و برای نمایش کسر دوم یعنی
باید ۲ قسمت از ۵ قسمت را رنگ کنیم.
با توجه به اینکه مخرجها برابرند، برای حاصلجمع آنها شکلی پنجقسمتی مشابه دو شکل دیگر رسم کرده و ۱ قسمت رنگشده کسر اول و ۲ قسمت رنگشده کسر دوم را در آن نشان میدهیم. در آخر، تعداد قسمتهای رنگشده را میشماریم. همانطور که در شکل زیر هم میبینید، در مجموع از ۵ قسمت، ۳ قسمت رنگشده خواهیم داشت. این یعنی اینکه حاصلجمع دو کسر برابر با است.
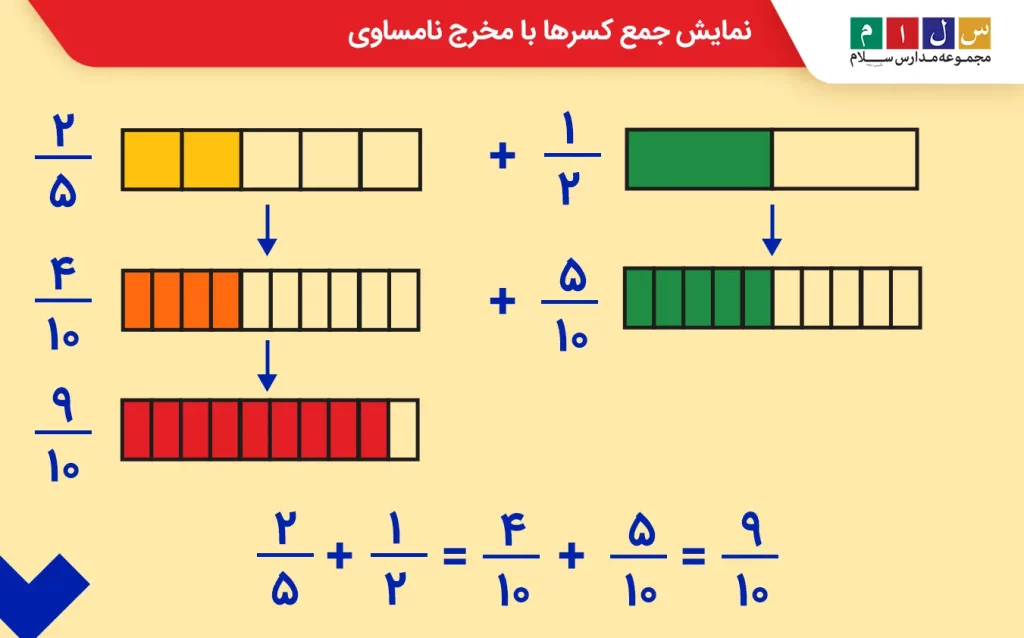
اکنون با یک مثال، حالتی را که مخرجها نامساوی هستند، مورد بررسی قرار میدهیم. عبارت زیر را در نظر بگیرید:
با توجه به اینکه مخرجها برابر نیستند، ابتدا با استفاده از کوچکترین مضرب مشترک، مخرجها را یکسان میکنیم. کوچکترین مضرب مشترک ۲ و ۵ عدد ۱۰ است. پس باید بهشکل زیر صورت و مخرج دو کسر را در عددی ضرب کنیم که مخرجها مساوی ۱۰ شوند:
مانند تصویر زیر، شکل کسرهای معادل یعنی را رسم میکنیم. برای کسر
قسمت از ۱۰ قسمت و برای کسر
قسمت از ۱۰ قسمت را رنگ میزنیم. همانطور که میبینید، مجموع خانههای رنگشده ۹ تا و درنتیجه حاصلجمع کسرها
است.
جمع کسرها روی محور
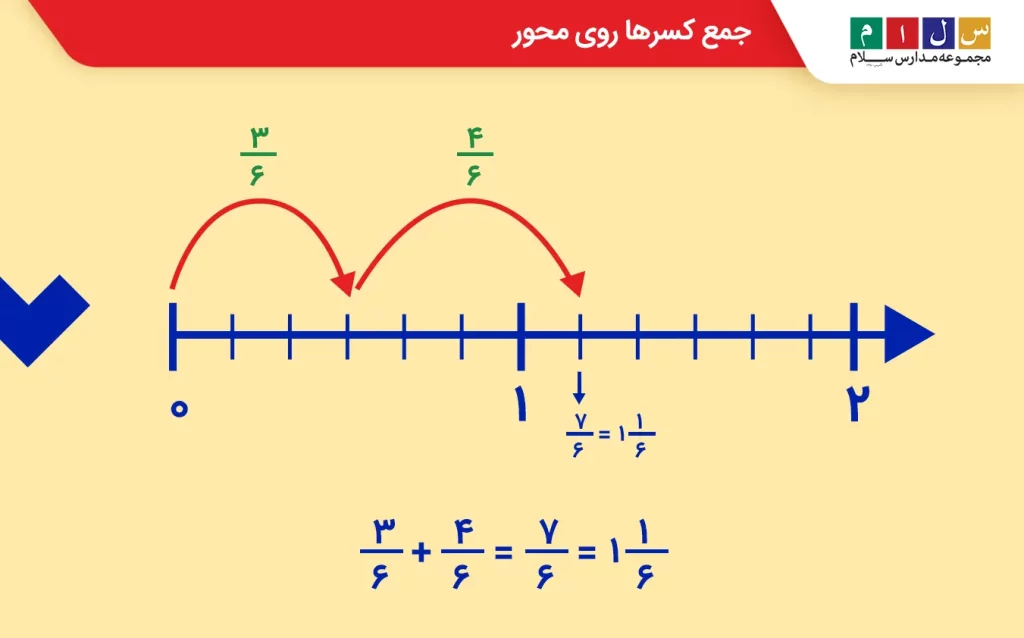
برای نمایش جمع کسرها روی محور اعداد، باید به مخرج کسرها توجه کنیم که مساوی باشند. اگر مساوی نبودند، با روشی که در بخشهای قبل توضیح دادیم، مخرج مشترک میگیریم. بهعنوان مثال، برای نشان دادن حاصلجمع روی محور ابتدا مخرجهای آن را با مخرج مشترک گرفتن یکسان میکنیم.
- مضربهای ۳: ۳، ۶، ۹، ۱۲، ۱۵ و غیره.
- مضربهای ۲: ۲، ۴، ۶، ۸ و غیره.
کوچکترین مضرب مشترک ۲ و ۳ عدد ۶ است. پس مخرج مشترک دو کسر را ۶ قرار میدهیم. خواهیم داشت:
با توجه به اینکه مخرج دو کسر ۶ است، یک محور رسم کرده و هر واحد آن را به ۶ قسمت مساوی تقسیم میکنیم. ابتدا کسر اول را روی محور نشان میدهیم؛ از صفر شروع کرده و با یک کمان بهاندازه ۳ خانه جلو میرویم و با انتهای کمان آن را مشخص میکنیم.
حالا نوبت کسر دوم است. این بار از انتهای کمان اول یک کمان رسم میکنیم و بهاندازه ۴ خانه میشماریم. انتهای کمان دوم عدد یا بهعبارتی
را نشان میدهد که همان حاصلجمع دو کسر است.
اگر پس از جمع کسرها میخواهید حاصل را اعشاری کنید، یادگیری تبدیل کسر به اعشار در ماشین حساب به شما کمک میکند.
جمع کسر و عدد صحیح
گاهی اوقات در برخی از عبارتهای ریاضی لازم است مجموع یک کسر و عدد صحیح را بهدست آوریم. برای مثال، در عبارت عدد صحیح ۳ با کسر
جمع شده است. در چنین حالتی، اولین کاری که باید انجام دهیم قرار دادن مخرج ۱ برای عدد صحیح و تبدیل آن به کسر است.
پس از آن، مانند آنچه در بخشهای قبل گفتیم، برای یکسان کردن مخرجها بهصورت زیر مخرج مشترک میگیریم:
جواب بهدستآمده یک کسر بزرگتر از واحد است و میتوان آن را به عدد مخلوط تبدیل کرد:
جمع اعداد مخلوط
فرض کنید میخواهیم حاصلجمع زیر را بهدست آوریم:
برای جمع کردن این دو عدد مخلوط ابتدا باید آنها را بهصورت زیر به کسر تبدیل کنیم:
پس از تبدیل اعداد مخلوط به کسر، میتوانیم بهراحتی حاصلجمع را تعیین کنیم.
نمونه سؤال جمع کسرها با جواب برای کلاس پنجم و ششم
حاصل عبارتهای زیر را بیابید.
الف)
ب)
ج)
د)
الف): این عبارت شامل سه کسر با مخرج نامساوی است. پس اولین کاری که باید انجام دهیم، مخرج مشترک گرفتن با استفاده از کوچکترین مضرب مشترک اعداد ۵، ۱۰ و ۱۵ است. مضربهای این سه عدد عبارتاند از:
- مضربهای ۵: ۵، ۱۰، ۱۵، ۲۰، ۲۵، ۳۰، ۳۵ و غیره.
- مضربهای ۱۰: ۱۰، ۲۰، ۳۰، ۴۰ و غیره.
- مضربهای ۱۵: ۱۵، ۳۰، ۴۵ و غیره.
کوچکترین مضربی که بین هر سه عدد مشترک است، عدد ۳۰ است. بنابراین، باید صورت و مخرج هر سه کسر را در عددی ضرب کنیم که مخرجها برابر ۳۰ شوند. خواهیم داشت:
ب): برای محاسبه این عبارت، ابتدا باید اعداد مخلوط به کسر تبدیل شوند.
مخرج هر سه کسر حاصل برابر نیست. بنابراین، مخرج مشترک میگیریم و سپس حاصلجمع را بهدست میآوریم.
د): اول از همه عبارت داخل پرانتز را محاسبه میکنیم. این عبارت شامل یک عدد صحیح و یک کسر است که برای بهدست آوردن مجموع آنها ابتدا باید مخرج عدد صحیح را ۱ قرار دهیم.
بنابراین، خواهیم داشت:
عبارت حاصل را طبق قاعده تقسیم کسرها محاسبه میکنیم. به این صورت که علامت تقسیم را به ضرب تغییر داده و جای صورت و مخرج کسر دوم را عوض میکنیم.
سخن پایانی
در این مقاله، با نحوه جمع کردن کسرها آشنا شدیم و یاد گرفتیم چگونه کسرهایی که مخرج مساوی یا نامساوی دارند را با هم جمع کنیم. تمام قواعدی که برای جمع کسرها بهکار برده شد، برای عمل تفریق آنها نیز مورد استفاده قرار میگیرد. تنها تفاوتی که بین آنها وجود دارد این است که بهجای عمل جمع، عمل تفریق انجام میشود. قانون کلی برای جمع کسرها، مساوی بودن مخرج آنها است. اگر مخرجها نامساوی باشند، باید با مخرج مشترک گرفتن آنها را مساوی کنیم. زمانی که مخرجها مساوی هستند، عمل جمع بهراحتی صورت میگیرد. کافیست صورتها را جمع کنیم و مخرج را بدون تغییر نگه داریم.









