فهرست مطالب
Toggleمحیط اشکال هندسی را از طریق جمع ضلعهای آنها با یکدیگر حساب میکنیم. همانطور که در مقاله محیط مثلث گفتیم، برای محاسبه محیط مثلثها کافیست اندازه ۳ ضلع آنها را با یکدیگر جمع بزنیم. محیط مثلث متساویالساقین هم مثل دیگر مثلثها از طریق جمع ۳ ضلع آن با یکدیگر به دست میآید. البته برای محاسبه محیط مثلث متساویالساقین روش دیگری هم وجود دارد که به ویژگیهای خاص این شکل هندسی وابسته است. ما در اینجا و در ادامه مباحث محیط و مساحت اشکال هندسی قرار است به بررسی جزئیات محیط مثلث متساویالساقین و فرمول آن بپردازیم.
محیط مثلث متساوی الساقین | توضیح مفهومی
مثلث متساویالساقین دارای ۲ ضلع برابر بهنام «ساق» و ضلع سومی بهنام «قاعده» است. دلیل تفاوت فرمول محیط این مثلث با دیگر انواع مثلثها، ۲ ساق مثلث متساوی الساقین هستند. برای درک بهتر این مسئله نگاهی به تصویر زیر بیندازید:
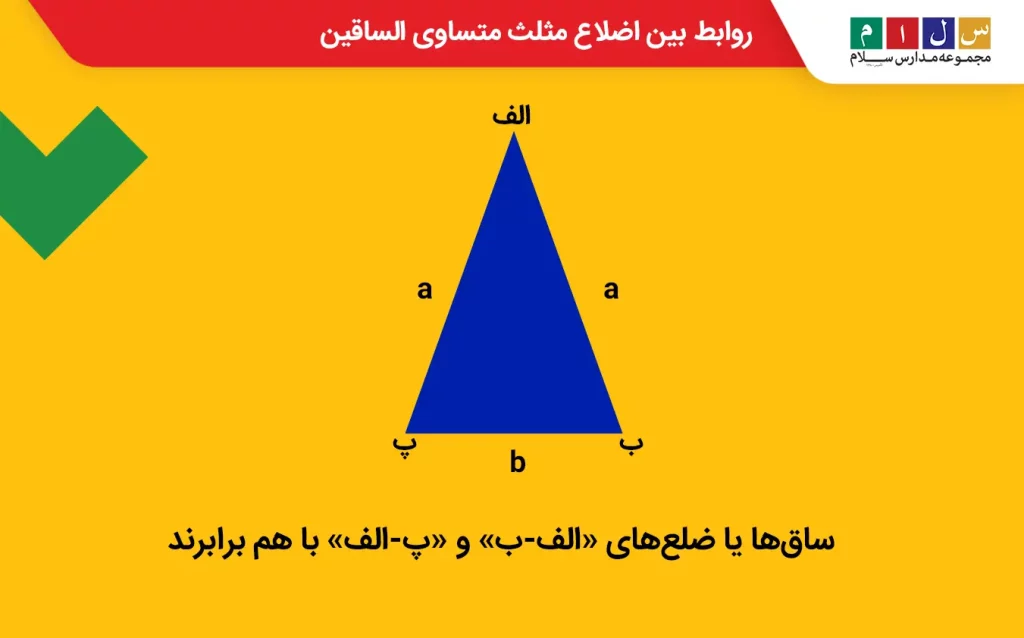
چون ۲ ضلع مثلث متساویالساقین با هم مساویاند، در تعریف محیطش میتوان گفت:
قاعده + ۲ × ساق = محیط مثلث متساویالساقین
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
فرمول محیط مثلث متساوی الساقین
باتوجه به اینکه ۲ ساق مثلث متساویالساقین با یکدیگر برابرند، میتوان آنها را با نمادی مشخص مانند الف نامگذاری کرد و فرمول اصلی محیط مثلث را به این صورت برای مثلث متساویالساقین باز نوشت:

ب + الف + الف = محیط مثلث متساویالساقین
یا
ب + الف × ۲ = محیط مثلث متساویالساقینیا
اگر توضیحات بالا را بهصورت نمادهای جبری ریاضی بنویسیم، به این صورت در میآید:
P = a + a + b = ۲ × a + b
محاسبه محیط مثلث متساوی الساقین با زاویه قائمه
گاهیاوقات مثلث متساویالساقین با مثلث قائمالزاویه ترکیب میشود و یک «مثلث متساویالساقین با زاویه قائمه» میسازد. به تصویر زیر نگاه کنید.
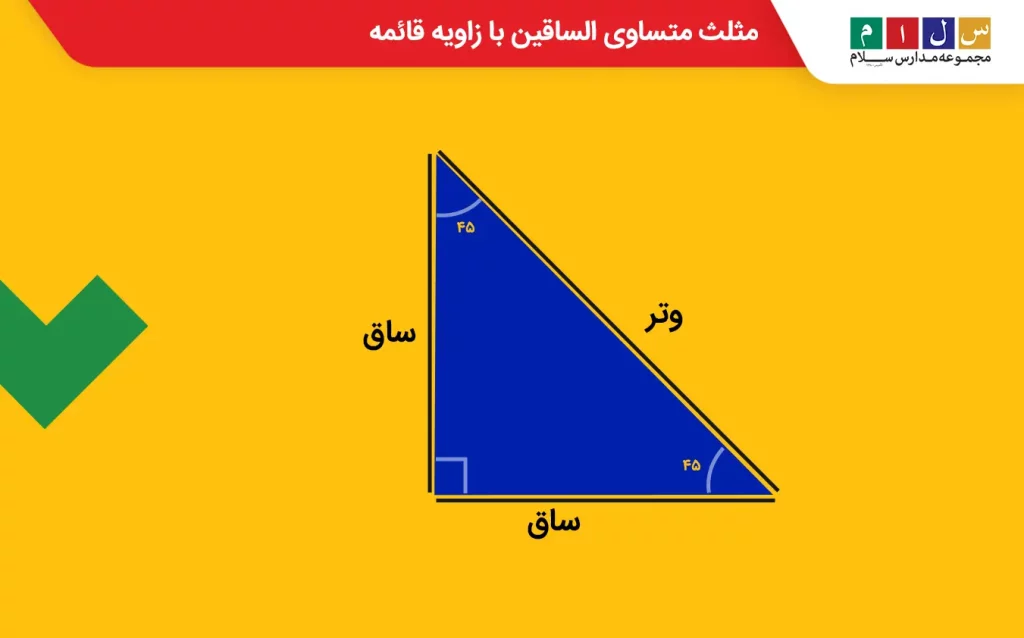
همانطور که در تصویر بالا مشاهده میکنید، نام ضلع مقابل زاویه قائمه «وتر» است. برای محاسبه وتر در مثلثهای قائمالزاویه از فرمول زیر استفاده میشود:
h=√۲×a
پس اگر در «مثلث متساویالساقین با زاویه قائمه» تنها اندازه وتر را داشته باشیم، میتوانیم به کمک آن محیط مثلث را حساب کنیم. بهعنوانمثال:
- اگر اندازه وتر یک مثلث قائمالزاویه ۶ سانتیمتر باشد، محیط آن چقدر میشود؟
جواب: ابتدا بهکمک فرمول وتر، اندازه ضلعهای مجاور با زاویه قائمه را حساب میکنیم:
h= √۲ × a
۶= ۱ ÷ ۴۱× a
a=۶÷۱/۴۱=۴/۲۵
حالا که اندازه ساقها (a) را به دست آوردیم، آن را در فرمول اصلی محیط مثلث متساویالساقین میگذاریم:
P = ۲ × a + b
P = ۲ × ۴/۲۵ + ۶
P = ۱۴/۵
پیشنهاد مطالعه: محاسبه محیط مثلث قائم الزاویه
مثال برای محیط مثلث متساوی الساقین
حالا که با روشهای مختلف محاسبه محیط مثلث متساویالساقین آشنا شدیم، بیایید برای یادگیری بهتر و عمیقتر این مبحث، مثالهای زیر را با هم حل کنیم.
مثال اول: محیط مثلث متساوی الساقین با ۳ ضلع
اگر اندازه ساقهای مثلث متساویالساقین ۴ سانتیمتر و اندازه ضلع سوم (قاعده) آن ۵ سانتیمتر باشد، محیط آن چند سانتیمتر میشود؟جواب: چون اندازه ساقها و قاعده مثلث را داریم، با استفاده از فرمول اصلی محیط مثلث متساویالساقین، اندازه آن را محاسبه میکنیم:

P = ۲ × ۴ + ۵
P = ۱۳ = ۵ + ۸
مثال دوم: محاسبه محیط مثلث متساوی الساقین با فرمول وتر
اندازه ساقهای محیط «مثلث متساویالساقین با زاویه قائمه» ۵ سانتیمتر است، اندازه وتر و محیط این مثلث را حساب کنید:جواب: برای محاسبه وتر در «مثلث متساویالساقین با زاویه قائمه» از فرمول زیر استفاده میکنیم:

h= √۲ × a
۵ × h= ۱/۴۱
h=۷/۰۵
حالا که اندازه ضلع سوم (وتر) را به دست آوردیم، آن را در فرمول اصلی محیط مثلث متساویالساقین میگذاریم:
P = ۲ × ۵ + ۷/۰۵
P = ۱۷/۰۵ = ۷/۰۵ + ۱۰
پیشنهاد مطالعه: محیط مثلث متساوی الاضلاع
مثال سوم: محاسبه ساق مثلث متساوی الساقین بهکمک محیط و قاعده
محیط یک مثلث متساویالساقین ۲۰ سانتیمتر و قاعده آن ۸ سانتیمتر است. اندازه ساقهای این مثلث را حساب کنید.جواب: وقتی اندازه محیط و قاعده مثلث را داشته باشیم، میتوانیم آنها را در فرمول اصلی محیط مثلث متساویالساقین جایگذاری کنیم و اندازه ساقها را به دست آوریم

P = ۲ × a + b
۲۰ = ۲ × a + ۸
۲۰ ‒ ۸ = ۲ × a
۱۲ = ۲ × a
a = ۱۲ ÷ ۲= ۶
سخن پایانی
محیط مثلث متساویالساقین مساوی با «۲ ضربدر ساق بهاضافه قاعده (b + a × ۲P = )» است. این فرمول تفاوت چندانی با فرمول اصلی محیط مثلث ندارد؛ فقط چون ساقهای مثلث متساویالساقین با هم برابرند، بهجای جمعشان با یکدیگر، یکی از آنها را ضربدر ۲ میکنیم. محیط مثلث متساویالساقین با زاویه قائمه را میتوان به کمک فرمول وتر هم به دست آورد، زیرا اندازه وتر آن، برابر با جذر ۲ ضربدر اندازه ساق (a) است. ما در این مقاله سعی کردیم حالتهای مختلفی را که ممکن است از مبحث محیط مثلث متساویالساقین سوال طرح شود، بیان کنیم. امیدواریم این مقاله در یادگیری بهتر و عمیقتر این مبحث به شما کمک کرده باشد.









