اگر به حرکت چرخ‌وفلک، چرخ‌های اتومبیل و دوچرخه یا ملخ‌های هلی‌کوپتر دقت کرده باشید، می‌بینید که پس از چرخش بهاندازه مشخصی دوباره به حالت اولیه برمی‌گردند؛ یعنی پس از دوران با زاویه معین روی خودشان منطبق می‌شوند. همه این‌ها نمونه‌هایی از تقارن چرخشی هستند که در این مقاله قصد داریم به آن بپردازیم.
پیشنهاد مطالعه: تقارن چیست؟
تقارن چرخشی چیست؟
یک طلق شیشه‌ای را روی یک مربع به‌شکل زیر قرار دهید و مربعی با همین ابعاد روی طلق بکشید، سپس، با مداد یا چیزی شبیه به آن طلق را در نقطه مرکزی نشان‌داده‌شده نگه دارید.
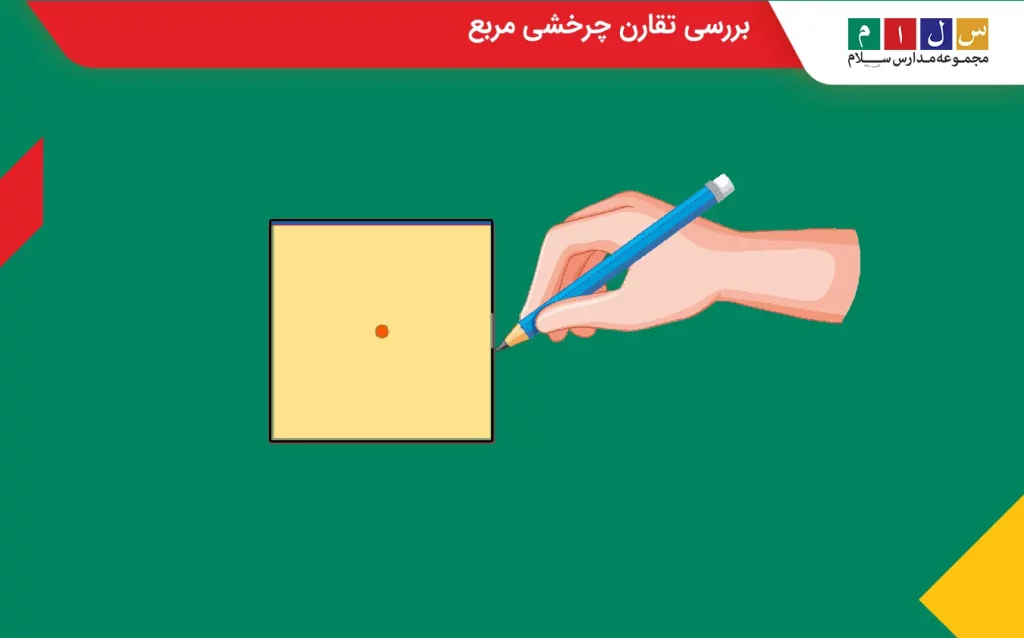
حالا طلق را حول نقطه مرکزی بهاندازه ۹۰ درجه و سپس ۱۸۰، ۲۷۰ و ۳۶۰ درجه دوران دهید. همان‌طور که در تصویر زیر مشاهده می‌کنید، مربع پس از دوران با اندازه‌های ذکرشده، روی خودش منطبق میشود. به‌عبارت دیگر، یک مربع در دوران ۳۶۰ درجه حول مرکزش، ۴ بار به حالت اولیه‌اش برمی‌گردد. این نشان می‌دهد که مربع دارای تقارن چرخشی است.
به‌طور کلی، اگر شکلی را با زاویه مشخص (۱۸۰ درجه یا کمتر) حول یک نقطه بچرخانیم، طوری که پس از چرخش، شکل روی خودش بیفتد و به حالت اولیه‌اش بازگردد، آن شکل دارای تقارن چرخشی خواهد بود.
نکته: فرقی نمی‌کند که دوران شکل در جهت حرکت عقربه‌های ساعت صورت گیرد یا خلاف جهت آن.
کوچک‌ترین و اولین زاویه‌ای که شکل پس از دوران با آن مقدار روی خودش منطبق میشود را زاویه چرخش و تعداد دفعاتی که شکل در دوران ۳۶۰ درجه روی خودش منطبق میشود را مرتبه تقارن چرخشی می‌گویند. برای مثال، در مربع شکل بالا که در دوران۳۶۰ درجه حول مرکزش ۴ بار روی خودش منطبق شد، مرتبه تقارن ۴ و زاویه چرخش ۹۰ درجه است.
مثال هایی از تقارن چرخشی ریاضی ششم
در این بخش، برای یادگیری بیشتر، به حل چند مثال از تقارن چرخشی در اشکال مختلف می‌پردازیم.
مثال ۱: آیا فرفره نشان‌داده‌شده در شکل زیر تقارن چرخشی دارد؟
جواب: فرفره شکل بالا دارای چهار پر یکسان است که همگی در مرکز به هم متصل هستند و حول این مرکز می‌چرخند. همان‌طور که در شکل زیر نشان داده‌ایم، وقتی فرفره را با فوت کردن به‌حرکت درمی‌آوریم، در یک چرخش ۳۶۰ درجه چهار بار به حالت اولیه‌اش برمی‌گردد. بنابراین، فرفره نسبت به مرکزش تقارن چرخشی مرتبه چهار دارد.
پیشنهاد مطالعه: مرکز تقارن چیست؟
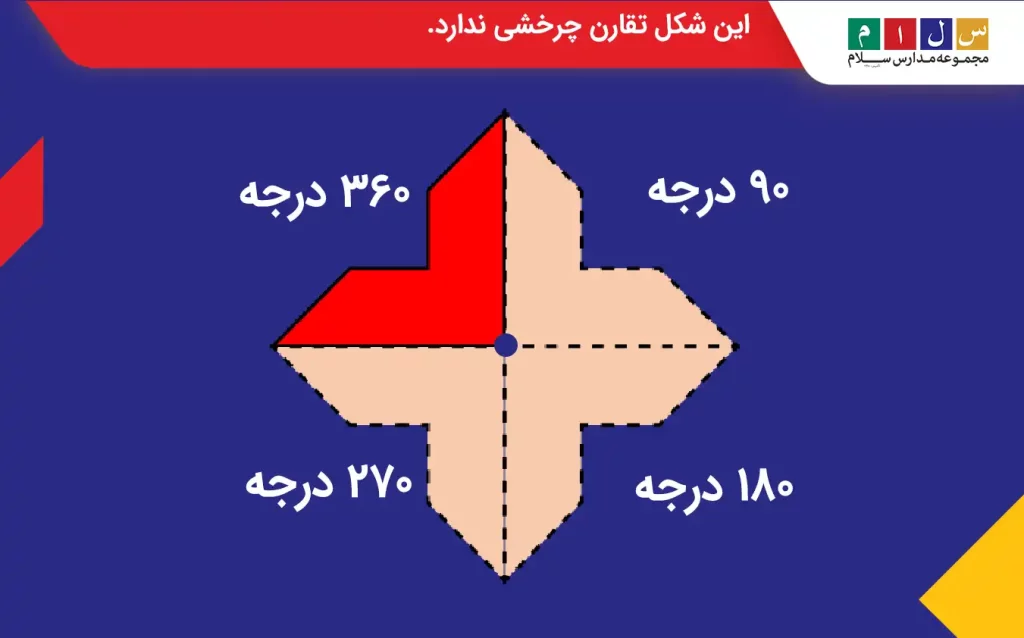
مثال ۲: آیا شکل زیر حول نقطه مشخص‌شده، دارای تقارن چرخشی است؟
جواب: این شکل تقارن چرخشی ندارد، زیرا اگر مانند شکل زیر آن را یک دور کامل (۳۶۰ درجه) بچرخانیم، در زاویه ۱۸۰ درجه و کمتر از آن روی خودش منطبق نمی‌شود.
مثال ۳: هر یک از شکل‌های زیر را حول نقطه داده‌شده چند درجه بچرخانیم تا شکل روی خودش منطبق شود؟
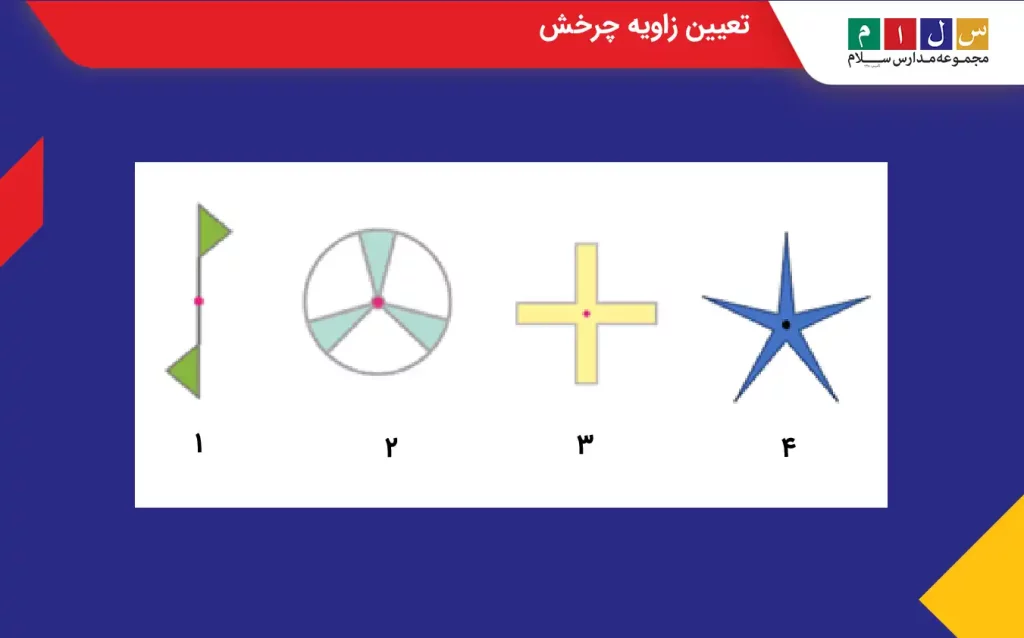
جواب: هر یک از شکل‌ها را جداگانه بررسی می‌کنیم:
- شکل (۱): از ۲ پره یکسان ساخته شده است و باید ۱۸۰ درجه آن را بچرخانیم تا روی خودش منطبق شود.
- شکل (۲): شامل ۳ پره همانند است و باید ۱۲۰ درجه (۳۶۰ درجه تقسیم بر ۳) چرخانده شود تا روی خودش بیفتد.
- شکل (۳): این شکل از ۴ قسمت مساوی تشکیل شده و پس از چرخش ۹۰ درجه (۳۶۰ درجه تقسیم بر ۴) روی حالت اولیه قرار می‌گیرد.
- شکل (۴): ستاره پنج‌رأس، ۵ زاویه مساوی دارد. بنابراین، باید ۷۲ درجه (۳۶۰ درجه تقسیم بر ۵) آن را دوران دهیم تا روی شکل اولیه‌اش منطبق شود.
مثال ۴: شکل زیر در چه زاویه‌هایی روی خودش منطبق میشود؟
جواب: شکل فوق، نماد بازیافت است و مانند یک مثلث متساویالاضلاع به‌نظر می‌رسد. ازآنجا که مثلث متساویالاضلاع سه رأس و سه ضلع برابر دارد، در زاویه‌های ۱۲۰، ۲۴۰ و ۳۶۰ درجه روی خودش منطبق میشود.
تقارن چرخشی اشکال هندسی
با توجه به توضیحاتی که تا اینجا داده شد، می‌توانیم به‌راحتی تقارن چرخشی اشکال هندسی را بررسی کنیم. در جدول زیر، مشخص کرده‌ایم کدام یک از اشکال هندسی تقارن چرخشی دارند و کدام یک ندارند. اگر درباره اشکال مختلف تقارن، کنجکاو هستید پیشنهاد می‌کنیم به انواع تقارن از مقاله های سلام سر بزنید.
| شکل | تقارن چرخشی |
 | دارد |
 | ندارد |
 | ندارد |
 | دارد |
 | دارد |
 | دارد |
 | دارد |
 | دارد |
 | دارد |
 | ندارد |
 | ندارد |
| انواع ذوزنقه | ندارد |
| فردضلعیهای منتظم | دارند |
| زوجضلعیهای منتظم | دارند |
تفاوت تقارن مرکزی و تقارن چرخشی
طبق تعریف تقارن چرخشی، اگر شکلی را بهاندازه نیمدور یا کمتر حول یک نقطه دوران دهیم، پس از دوران آن شکل روی خودش منطبق میشود. حالا اگر زاویه چرخش یک شکل ۱۸۰ درجه باشد، یعنی با چرخش نیمدور، شکل روی خودش منطبق شود، در این‌صورت، آن شکل علاوه‌بر تقارن چرخشی، تقارن مرکزی نیز دارد. درواقع، میتوان گفت که تقارن مرکزی حالت خاصی از تقارن چرخشی است. به‌عنوان مثال، یک مستطیل چون تقارن چرخشی ۱۸۰ درجه دارد، تقارن مرکزی هم خواهد داشت.
نکته: اگر یک شکل تقارن مرکزی داشته باشد، تقارن چرخشی نیز دارد، اما اگر شکل موردنظر تقارن چرخشی داشته باشد، ممکن است دارای تقارن مرکزی نباشد. برای مثال، همان‌طور که در شکل زیر نشان داده شده است، مثلث متساویالاضلاع با وجود اینکه تقارن چرخشی ۱۲۰ درجه دارد، دارای تقارن مرکزی نیست.
سخن پایانی
اگر یک شکل پس از دوران ۱۸۰ درجه یا کمتر حول یک نقطه، روی خودش منطبق شود، آن شکل تقارن چرخشی خواهد داشت. کوچک‌ترین و اولین زاویه‌ای که شکل پس از دوران با آن مقدار روی خودش منطبق میشود را زاویه چرخش و تعداد دفعاتی که شکل در دوران ۳۶۰ درجه روی خودش منطبق میشود را مرتبه تقارن چرخشی می‌گویند. در تقارن چرخشی فرقی نمی‌کند که جهت چرخش در جهت حرکت عقربه‌های ساعت باشد یا خلاف آن. بسیاری از اشکال هندسی نسبت به مرکزشان دارای تقارن چرخشی هستند، ازجمله دایره، بیضی، مربع، لوزی، مستطیل، متوازیالاضلاع، مثلث متساویالاضلاع، فردضلعیها و زوجضلعیهای منتظم.
سؤالات متداول
- تقارن چرخشی چیست؟
نوعی تقارن است که در آن شکل پس از چرخش بهاندازه معین (۱۸۰ درجه یا کمتر) حول یک نقطه، به حالت اولیه خود بازمیگردد. - تقارن چرخشی چه فرقی با تقارن مرکزی دارد؟
در تقارن مرکزی، شکل پس از چرخش بهاندازه نیمدور (۱۸۰ درجه) حول یک نقطه مرکزی، روی خودش منطبق میشود. پس میتوان گفت که تقارن مرکزی حالت خاصی از تقارن چرخشی است. - آیا شکلی که تقارن چرخشی دارد، تقارن مرکزی هم دارد؟
شکلی که دارای تقارن چرخشی است، ممکن است تقارن مرکزی داشته باشد یا نداشته باشد. - آیا شکلی که تقارن مرکزی دارد، تقارن چرخشی هم دارد؟
بله. ازآنجا که تقارن مرکزی یک نوع تقارن چرخشی است، هر شکلی که تقارن مرکزی داشته باشد، تقارن چرخشی نیز دارد. - کدام یک از اشکال هندسی، تقارن چرخشی دارند؟
دایره، بیضی، مربع، لوزی، مستطیل، متوازیالاضلاع، مثلث متساویالاضلاع، فردضلعیها و زوجضلعیهای منتظم تقارن چرخشی دارند. - کدام شکل تقارن چرخشی دارد ولی تقارن مرکزی ندارد؟
تمام فردضلعیهای منتظم تقارن چرخشی دارند اما تقارن مرکزی ندارند. - کدام شکل هم تقارن چرخشی دارد هم تقارن مرکزی؟
دایره، بیضی، مربع، لوزی، مستطیل، متوازیالاضلاع و زوجضلعیهای منتظم هر دو تقارن چرخشی و مرکزی را دارند.
