فهرست مطالب
Toggleاعداد اول، گروهی از اعداد در ریاضی هستند که تنها دو عامل دارند و بدون باقیمانده تنها بر عدد ۱ و خودشان تقسیم میشوند. در این مقاله، به بررسی دقیقتر این اعداد خواهیم پرداخت، به شما خواهیم گفت که اعداد اول چه ویژگیهایی دارند و چگونه میتوانیم از طریق روشهای مختلف، اول بودن یک عدد را تشخیص دهیم.
تعریف اعداد اول
اعداد اول، اعداد طبیعی بزرگتر از یک هستند که تنها دو عامل دارند. منظور از عامل، اعدادی هستند که در هم ضرب میشوند تا عدد موردنظر حاصل شود. دو عامل اعداد اول شامل ۱ و خود عدد است. این بدین معنی است که اعداد اول را فقط میتوان بر خودشان و عدد یک تقسیم کرد، بدون اینکه باقیماندهای وجود داشته باشد.
همانطور که گفتیم، اعداد اول اعدادی بزرگتر از یک هستند، یعنی عدد ۱ را نمیتوان بهعنوان عدد اول در نظر گرفت. دلیل آن این است که عدد ۱ را میتوان تنها بر خودش یعنی یک تقسیم کرد و از اینرو، این عدد دو عامل ندارد.
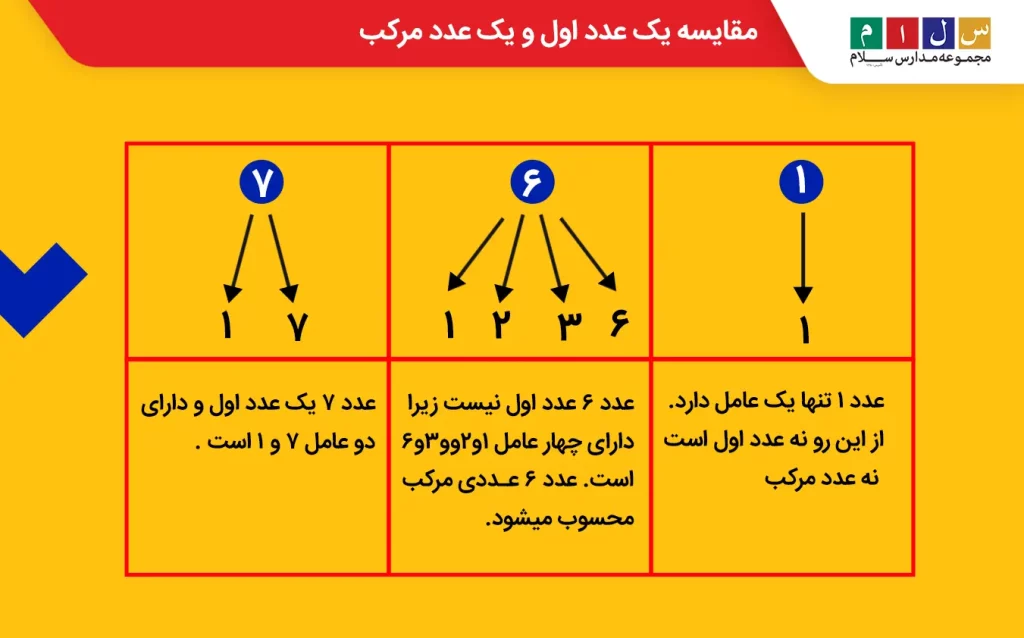
بگذارید یک مثال بزنیم تا اعداد اول را بهتر درک کنید. دو عدد ۶ و ۷ را در نظر بگیرید. عدد ۶ علاوهبر یک و خودش، بر ۲ و ۳ نیز بخشپذیر است، یعنی بیش از دو عامل دارد. بنابراین، عدد ۶ عدد اول محسوب نمیشود، اما در مقابل، عدد ۷ عددی است که تنها بر یک و خودش یعنی ۷ بخشپذیر است و ازاینرو، یک عدد اول بهشمار میرود.
ویژگی های اعداد اول
در این بخش، ویژگیهای اعداد اول را بیان میکنیم. این ویژگیها عبارتاند از:
- عدد اول یک عدد طبیعی بزرگتر از یک است.
- اعداد اول تنها دو عامل دارند: عدد یک و خود عدد.
- عدد ۲ بهعنوان کوچکترین عدد اول، تنها عدد اولی است که زوج است.
- هر عدد مرکب را میتوان بهصورت حاصلضرب اعداد اول بیان کرد.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
تفاوت اعداد اول و مرکب
پاسخ سوال تفاوت اعداد اول و اعداد مرکب چیست را در جدول زیر مشاهده میکنید:
| اعداد اول | اعداد مرکب |
| عدد اول یک عدد طبیعی بزرگتر از ۱ است که فقط دو عامل دارد: عدد ۱ و خود عدد. | عدد مرکب یک عدد طبیعی است که بیش از دو عامل دارد. |
| کوچکترین عدد اول ۲ است. | کوچکترین عدد مرکب ۴ است. |
| مثال: ۲، ۳، ۵، ۷، ۱۱، ۱۳ و غیره | مثال: ۴، ۶، ۸، ۹، ۱۰، ۱۲ و غیره |
پیشنهاد مطالعه : مجموعه اعداد
اعداد اول را چگونه تشخیص دهیم؟
تا اینجا توضیح دادیم که عدد اول چیست و چه ویژگیهایی دارد. اکنون این سؤال پیش میآید که چگونه میتوان اعداد اول را تشخیص داد و آیا روش خاصی برای تعیین این اعداد وجود دارد؟
با توجه به توضیحاتی که در بخشهای قبل داده شد، میتوان گفت یک روش پیدا کردن عدد اول، بررسی عاملهای آن عدد است. اگر عدد موردنظر تنها دو عامل داشته باشد، آن عدد یک عدد اول خواهد بود. البته، استفاده از این روش برای اعداد بزرگ معمولاً وقتگیر است.
آیا میدانید اعداد گویا، چه اعدادی هستند؟ برای درک بهتر این مفهوم، این مقاله را از دست ندهید.
در ادامه، روش و فرمولهای آسانتری برای یافتن اعداد اول ۱ تا ۱۰۰ را معرفی خواهیم کرد.
روش اول: غربال اعداد اول
در قرن سوم، ریاضیدانی یونانی بهنام اراتوستن روشی بسیار ساده برای یافتن اعداد اول پیدا کرد. این روش که غربال اراتوستن نام دارد، برای تعیین اعداد اول از عدد ۲ تا هر عدد دلخواهی قابل استفاده است. در اینجا ما این روش را برای اعداد ۲ تا ۱۰۰ بهکار میبریم و روش انجام آن را مرحلهبهمرحله توضیح میدهیم.
- مرحله ۱: ابتدا لیستی از اعداد ۲ تا ۱۰۰ را مطابق شکل زیر ایجاد میکنیم. از عدد ۱ صرفنظر میکنیم زیرا ۱ عدد اول نیست.
- مرحله ۲: از عدد ۲ شروع کرده و بهجز ۲ هر عددی که مضرب ۲ است را خط میزنیم؛ یعنی تمام اعداد زوج غیر از ۲.
- مرحله ۳: اکنون سراغ عدد خط نخورده بعدی یعنی عدد ۳ میرویم و بهجز ۳ هر عددی که مضرب ۳ است را خط میزنیم. برخی از این مضربها ممکن است در مرحله قبل خط خورده باشند. بنابراین، سراغ آنهایی میرویم که خط نخوردهاند.
- مرحله ۴: اکنون نوبت عدد خط نخورده بعدی یعنی عدد ۵ است. غیر از ۵ هر عددی را که مضرب ۵ است و خط نخورده است، خط میزنیم.
- مرحله ۵: عدد ۷ عدد خط نخورده بعدی در لیست اعداد است. بنابراین، باید بهجز ۷ هر عددی که مضرب ۷ است خط زده شوند. بعد از این مرحله، مانند شکل زیر تنها اعداد اول خط نخورده باقی میمانند.

روش دوم: فرمول اعداد اول
در این بخش، فرمولهایی را ارائه میکنیم که بهکمک آنها هم میتوان اعداد اول را تولید کرد و هم تشخیص داد که آیا عدد موردنظر یک عدد اول است یا خیر.
فرمول اول:
هر عدد اول غیر از ۲ و ۳ را میتوان بهشکل ۶n+۱ و ۶n-۱ (n≥۱) نوشت. بنابراین، با استفاده از این فرمولها میتوانیم اعداد اول بزرگتر از ۳ را تشخیص دهیم. برای مثال، اگر n=۱ باشد با کمک این دو فرمول اعداد اول ۵ و ۷ بهدست میآید:
۶ ( ۱ ) – ۱ = ۵
۶ ( ۱ ) + ۱ = ۷
توجه داشته باشید که هنگام استفاده از این روش، مضارب اعداد اول را در نظر نمیگیریم. بهعنوان مثال، اگرچه اعداد ۲۵ و ۴۹ را میتوان بهصورت ۲۴+۱ و ۴۸+۱ نوشت اما این اعداد عدد اول نیستند.
اکنون با یک مثال، نحوه استفاده از این فرمول برای تشخیص اول بودن یک عدد را توضیح میدهیم.
مثال: آیا عدد ۵۴۱ یک عدد اول است؟
جواب: برای بررسی اینکه آیا عدد ۵۴۱ عدد اول است یا نه، این عدد را بر ۶ تقسیم میکنیم. باقیمانده این تقسیم برابر با ۱ است و ازاینرو، میتوان ۵۴۱ را بهصورت ۱+(۹۰)۶نوشت. بنابراین، ۵۴۱ عدد اول محسوب میشود.
فرمول دوم:
برای تعیین اعداد اول بزرگتر از ۴۰ میتوانیم از فرمول n۲+n+۴۱ استفاده کنیم که در آن n=۰,۱, ۲, …, ۳۹ است.
مثالها:
(۰) ۲+ ۰ + ۴۱ = ۴۱
( ۱ ) ۲+ ۱ + ۴۱ = ۴۳
( ۲ ) ۲+۲+ ۴۱ = ۴۷
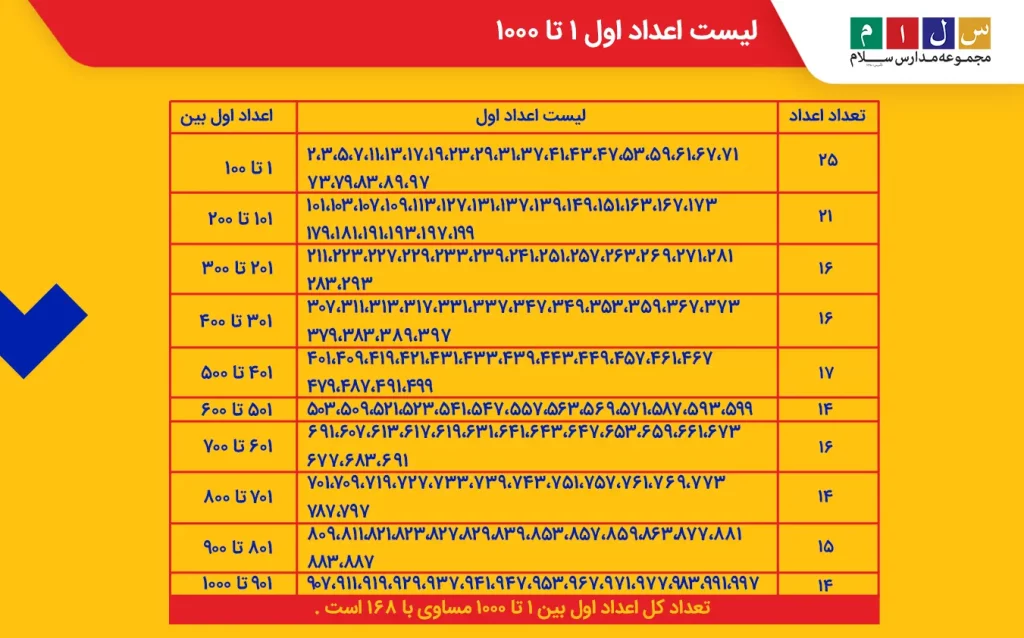
اعداد اول ۱ تا ۱۰۰۰ در فهرست اعداد اول
در این بخش، لیست اعداد اول ۱ تا ۱۰۰۰ را در قالب یک جدول آوردهایم. طبق جدول زیر، تعداد اعداد اول ۱ تا ۱۰۰ برابر با ۲۵ است.
سخن پایانی
در این مقاله، به پرسش اعداد اول چیست پاسخ دادیم و گفتیم که عدد اول یک عدد طبیعی بزرگتر از یک است که نمیتوان آن را بهصورت حاصلضرب دو عدد طبیعی بزرگتر از یک نوشت. این اعداد تنها بر یک و خودشان بخشپذیر هستند و ازاینرو، دو عامل دارند.
عدد ۲کوچکترین عدد اول و تنها عدد اولی است که زوج است. بهعبارت دیگر، غیر از ۲ هیچ عدد اول زوجی وجود ندارد. برای تشخیص اعداد اول، فرمولها و روشهای سادهای وجود دارد که در این مطلب با مثال به آنها پرداختیم. ازجمله این روشها، میتوان به روش غربال اشاره کرد که در آن اعداد غیراول مرحلهبهمرحله حذف میشوند.
سؤالات متداول
- اعداد اول چه اعدادی هستند؟
اعداد اول مجموعهای از اعداد طبیعی بزرگتر از یک هستند که تنها بر یک و خود عدد بخشپذیرند. - چرا یک عدد اول نیست؟
زیرا تنها یک عامل دارد و فقط بر خودش بخشپذیر است. - آیا ۷۹ عدد اول است؟
بله. زیرا تنها بر ۱ و خودش بخشپذیر است. - عدد یک اول است یا مرکب؟
عدد یک هیچکدام از ویژگیهای اعداد اول و مرکب را ندارد. بنابراین، نه عدد اول است نه عدد مرکب. - مجموع اعداد اول یکرقمی برابر با چند است؟
اعداد اول یکرقمی شامل ۲، ۳، ۵ و ۷ است. بنابراین، مجموع این اعداد برابر است با ۱۷. - اعداد اول ۱ تا ۱۰۰ را بنویسید.
۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹، ۲۳، ۲۹، ۳۱، ۳۷، ۴۱، ۴۳، ۴۷، ۵۳، ۵۹، ۶۱، ۶۷، ۷۱، ۷۳، ۷۹، ۸۳، ۸۹، ۹۷










یک پاسخ
مقاله بسیار خوب و آموزنده و عالی بود.