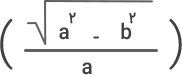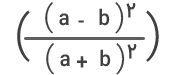بیضی به‌عنوان یک منحنی بسته مانند دایره‌ای به نظر می‌رسد که از دو طرف کشیده شده است. برخلاف دایره، برای محاسبه محیط بیضی فرمول ثابت و واحدی وجود ندارد، بلکه تاکنون چندین فرمول که همه آن‌ها یک مقدار تقریبی به‌دست می‌دهند برای تعیین محیط این شکل هندسی ارائه شده است. در این مقاله فرمول‌های موجود برای محاسبه محیط بیضی را معرفی خواهیم کرد.
محیط بیضی چیست؟
محیط یک بیضی از مجموعه نقاطی ساخته شده است که مجموع فاصله هر یک از آن‌ها از دو نقطه ثابت به‌نام کانون مقداری ثابت است. این مجموعه نقاط در کنار یکدیگر منحنی پیوسته‌ای تشکیل می‌دهند که همان مرز بیضی است. بنابراین، محیط بیضی برابر است با اندازه دورتادور بیضی (طول منحنی پیوسته). در شکل زیر، منحنی قرمزرنگ مرز بیضی یا همان محیط را نشان می‌دهد.
اولین نفری باشید که از اخبار و اطلاعیه‌های مرتبط با پایه تحصیلیتان باخبر می‌شود!
فرمول محیط بیضی چیست؟
محیط بیضی را می‌توان از فرمول‌های مختلفی محاسبه کرد، اما هیچ‌کدام از این فرمول‌ها مقدار دقیق محیط بیضی را به ما نمی‌دهند، زیرا تمامی آن‌ها فرمول‌های تقریبی هستند. فرمول‌های محاسبه محیط بیضی به انواع زیر تقسیم‌بندی می‌شوند:
- فرمول‌های تقریبی
- فرمول‌های رامانوجان
- فرمول های با سری بی‌نهایت
- فرمول‌های با انتگرال
در تمامی فرمول‌هایی که در ادامه معرفی می‌کنیم، با پارامترهای زیر سروکار داریم:
- a: شعاع بزرگ بیضی
- b: شعاع کوچک بیضی
- P: محیط بیضی
- e: خروج از مرکز بیضی
- h: یک ثابت در فرمول‌های محیط بیضی
محاسبه محیط بیضی با فرمول های تقریبی
در این بخش، سه فرمول تقریبی ساده و رایج برای محاسبه محیط بیضی معرفی می‌کنیم. این فرمول‌ها به‌صورت زیر هستند:
- فرمول ۱:
( P≈ π ( a+b
این فرمول به‌عنوان ساده‌ترین فرمول، فرمول محیط بیضی کلاس پنجم دبستان است که برای محاسبه محیط بیضی کلاس ششم ها و کلاس پنجمی‌ها می‌توانند از آن استفاده کنند.
- فرمول ۲:
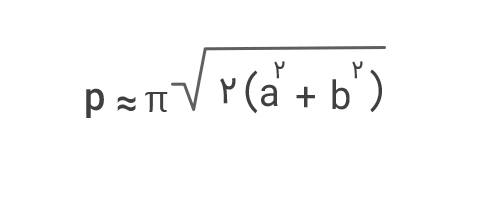
- فرمول ۳:
بهتر است از فرمول (۱) زمانی استفاده کنیم که شعاع‌های بزرگ و کوچک بیضی مقدارشان به هم نزدیک و تقریباً با هم برابر باشد. در چنین حالتی، شکل بیضی تقریباً شبیه به یک دایره است. هرچه شعاع‌ها اختلاف زیادی با هم داشته باشند، مقدار محیط به‌دست‌آمده از این فرمول و مقدار واقعی محیط بیضی اختلاف بیشتری خواهند داشت و درنتیجه خطای محاسباتی نیز بیشتر خواهد بود.
برخلاف فرمول (۱)، فرمول‌های (۲) و (۳) زمانی به‌کار می‌روند که اختلاف مقدار شعاع‌های بیضی زیاد باشد. البته فرمول (۲) مقداری بزرگ‌تر از مقدار واقعی و فرمول (۳) مقداری کمتر از مقدار واقعی محیط بیضی به ما می‌دهد. بنابراین، میانگین مقادیر به‌دست‌آمده از هر دو فرمول به مقدار واقعی محیط نزدیک‌تر خواهد بود.
محاسبه محیط بیضی با فرمول های رامانوجان
یک ریاضی‌دان معروف به‌نام «رامانوجان» (Ramanujan) فرمول‌های تقریبی دیگری برای تعیین محیط بیضی ارائه کرد که مقدار به‌دست‌آمده از آن‌ها نسبت به سه فرمول قبلی به مقدار واقعی نزدیک‌تر است. این فرمول‌های ساده و آسان اگرچه مقدار دقیق محیط بیضی را نشان نمی‌دهند، اما می‌توانند پاسخ دقیق‌تری ارائه دهند. این فرمول‌ها عبارت‌اند از:
فرمول ۴:
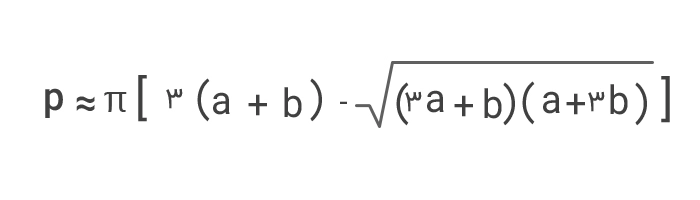
فرمول ۵ :
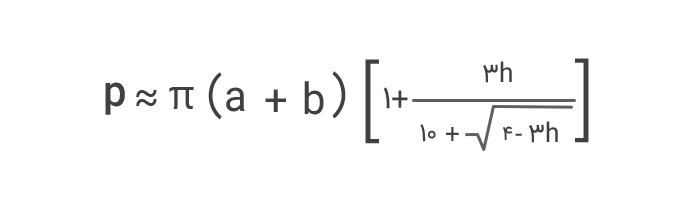
در اینجا h یک ثابت است و مقدار آن برابر است با:
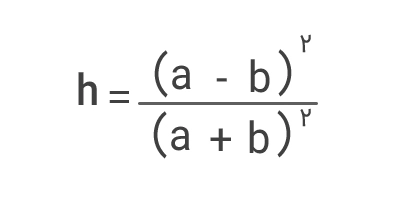
محاسبه محیط بیضی با سری بی نهایت
تا اینجا فرمول‌های تقریبی محیط بیضی را معرفی کردیم. در این بخش به معرفی فرمول‌هایی می‌پردازیم که پاسخ دقیق‌تری به ما می‌دهند. این فرمول‌ها به‌شکل سری‌های بی‌نهایت هستند. منظور از سری بی‌نهایت، مجموع بی‌نهایت جمله در یک دنباله است. سری‌های بی‌نهایتی که در این فرمول‌ها وجود دارد از نوع سری همگرا هستند و به یک عدد مشخص میل می‌کنند. در این نوع سری‌ها با هر جمله به مقدار دقیق محیط بیضی نزدیک‌تر می‌شویم.
فرمول‌های با سری بی‌نهایت به‌شرح زیر است:
- فرمول ۶:
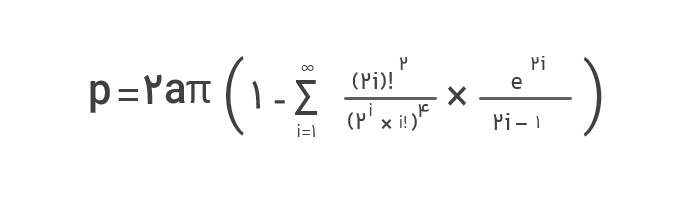
این فرمول برحسب ثابت e بیان شده است. e خروج از مرکز بیضی نام دارد و نشان‌دهنده مقدار کشیدگی یا فشردگی بیضی درمقایسه با یک دایره است. همان‌طور که در ابتدای مقاله هم اشاره کردیم، مقدار این ثابت برابر است با
چند جمله اول سری بالا به‌صورت زیر است:
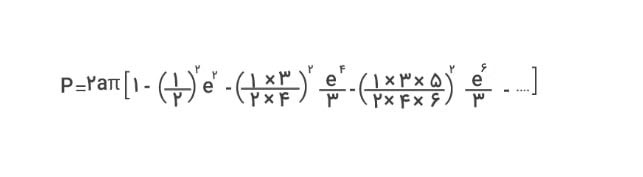
همان‌طور که می‌بینید، جملات این سری تا بی‌نهایت ادامه دارد. هرچه تعداد جملات بیشتری را در نظر بگیریم، به مقدار واقعی محیط نزدیک‌تر خواهیم شد.
- فرمول ۷:
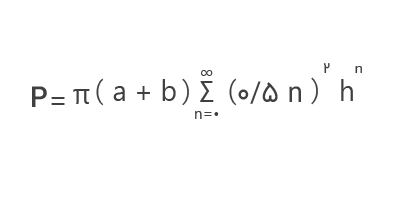
ثابت h که قبلاً هم آن را معرفی کردیم، از رابطه زیر به‌دست می‌آید:
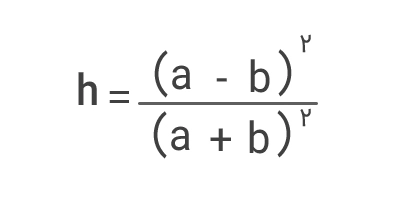
عبارت‌های نخست این سری به‌صورت زیر نوشته می‌شود:
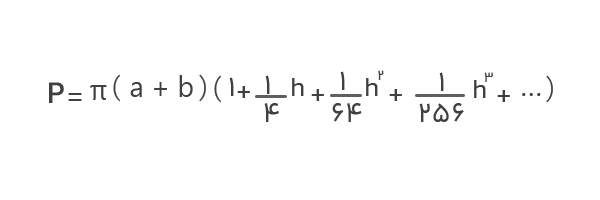
در این سری هرچه جلوتر می‌رویم، مقدار جملات کوچک‌تر می‌شود. البته نوشتن جملات بیشتر به ما کمک می‌کند پاسخ دقیق‌تری دریافت کنیم.
محاسبه محیط بیضی با انتگرال
می‌دانیم که طول کمان (L) تابعی مانند(y=f(x در بازه[ a , b ] از انتگرال زیر به‌دست می‌آید:
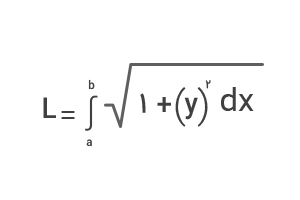
اگر بخواهیم طول کمان بیضی یعنی همان محیط بیضی را از این فرمول محاسبه کنیم، کافی‌ست به‌صورت زیر از معادله بیضی مشتق بگیریم:
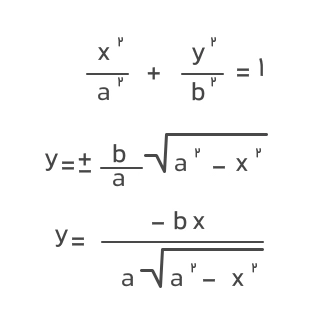
اکنون مشتق به‌دست‌آمده را در فرمول طول کمان جای‌گذاری می‌کنیم. اگر بازه انتگرال را ۰,a قرار دهیم یعنی تنها ربع اول بیضی را در نظر بگیریم، می‌توانیم طول یک‌چهارم کمان بیضی یا به‌عبارتی یک‌چهارم محیط بیضی را به‌دست آوریم. خواهیم داشت:
اگر این رابطه را در ۴ ضرب کنیم، فرمول محیط بیضی به‌دست می‌آید:
- فرمول ۸:
با استفاده از این رابطه می‌توان فرمول محیط بیضی را به‌صورت پارامتری نیز بیان کرد. برای این کار کافی‌ست x و y را برحسب پارامتر بنویسیم:
x=a cos θ
y=b sin θ
با جای‌گذاری این معادلات پارامتری در فرمول (۸) و تبدیل بازه انتگرال به 
فرمول پارامتری محیط بیضی به‌دست می‌آید:
فرمول ۹:
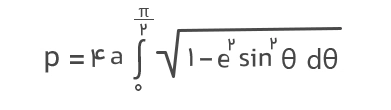
e خروج از مرکز بیضی است.
مقایسه محیط انواع بیضی با استفاده فرمول های مختلف
تمامی فرمول‌های محاسبه محیط بیضی ازنظر میزان دقت و خطا با هم متفاوت‌اند؛ طوری‌که اگر برای محاسبه محیط یک بیضی از فرمول‌های گوناگون استفاده کنیم، اختلاف پاسخ‌های به‌دست‌آمده از هر یک از فرمول‌ها با مقدار واقعی محیط متفاوت خواهد بود.
برای درک بهتر میزان دقت فرمول‌ها، در جدول زیر محیط بیضی را با استفاده از پنج فرمول (۲)، (۴)، (۵)، (۶) و (۷) برای مقادیر مختلف a و b به‌دست آورده‌ایم.
شکل |  |  |  |  |  |
| مقادیر a و b | a=۱۰b=۰ | a=۱۰b=۱ | a=۱۰b=۳ | a=۱۰b=۵ | a=۱۰b=۱۰ |
| فرمول ۲ | ۴۴/۴۲۹ | ۴۴/۶۵ | ۴۶/۳۸۵ | ۴۹/۶۷۳ | ۶۲/۸۳۲ |
| فرمول ۴ | ۳۹/۸۳۴ | ۴۰/۶۰۶ | ۴۳/۸۵۷ | ۴۸/۴۴۲ | ۶۲/۸۳۲ |
| فرمول ۵ | ۳۹/۹۸۴ | ۴۰/۶۳۹ | ۴۳/۸۵۹ | ۴۸/۴۴۲ | ۶۲/۸۳۲ |
| فرمول ۶ | ۴۲/۹۵۱ | ۴۳/۲۰۴ | ۴۵/۱۷۴ | ۴۸/۸۷۶ | ۶۲/۸۳۲ |
| فرمول ۷ | ۳۹/۸۸۴ | ۴۰/۶۲۳ | ۴۳/۸۵۹ | ۴۸/۴۴۲ | ۶۲/۸۳۲ |
| پاسخ دقیق | ۴۰ | … | … | … | تقریباً ۶۲/۸۳۲ |
همان‌طور که در جدول بالا مشاهده می‌کنید، زمانی که a و b با هم برابرند، بیضی به‌شکل دایره است و محیط به‌دست‌آمده از تمام فرمول‌ها مساوی با ۲a (در این مثال تقریباً ۶۲/۸۳۲) می‌شود. اما زمانی که b مساوی صفر است، بیضی به‌شکل یک خط دیده می‌شود و محیط آن برابر با a۴ (در اینجا ۴۰) خواهد بود. از میان داده‌های به‌دست‌آمده تنها مقدار حاصل از فرمول‌های (۴)، (۵) و (۷) به ۴۰ نزدیک است.
محاسبه محیط بیضی آنلاین
محاسبه محیط بیضی برخلاف سایر اشکال هندسی تاحدودی فرایند پیچیده‌تری دارد و تعیین مقدار آن با خطا همراه است. حسابگرهای آنلاین ابزارهایی کاربردی برای محاسبه محیط بیضی هستند که مقدار خطا را کاهش داده و محاسبات را با دقت بهتری انجام می‌دهند. یکی از این ابزارها حسابگر آنلاین گوگل است.
برای محاسبه محیط بیضی کافی‌ست معادل انگلیسی محیط بیضی یعنی ellipse perimeter را در گوگل جست‌وجو کنید. پس از جست‌وجو، در ابتدای صفحه کادری به‌صورت زیر مشاهده خواهید کرد.
پس از وارد کردن مقدار هر دو شعاع بیضی درون کادرهای مشخص‌شده می‌توانید مقدار محیط بیضی را در بالای دو کادر ببینید. علاوه‌بر پاسخ نهایی محیط، امکان مشاهده محاسبات در پایین کادر نیز وجود دارد. در تصویر زیر، نمونه‌ای از محاسبه محیط بیضی با حسابگر گوگل به‌ازای a=۷ و b=۵ نشان داده شده است.
علاوه‌بر این ابزار، ماشین‌حساب‌های آنلاین دیگری نظیر Omini Calculator وجود دارد که کار با آن نیز بسیار راحت است و قابلیت‌های دیگری هم دارد. می‌توانید به این سایت مراجعه کنید و مقدار محیط بیضی را با استفاده از آن به‌دست آورید.
سخن پایانی
در این مقاله درباره محیط بیضی و روش محاسبه آن صحبت کردیم و توضیح دادیم که محیط بیضی به زبان ساده برابر است با اندازه طول کمان بیضی. محاسبه محیط این شکل هندسی درمقایسه با سایر اشکال نسبتاً پیچیده‌تر است و فرمول‌های متعددی برای به‌دست آوردن آن وجود دارد که معمولاً یک مقدار تقریبی و همراه با خطا به ما می‌دهند. البته همان‌طور که گفتیم، برخی از این فرمول‌ها پاسخ‌های بهتری نسبت به دیگر فرمول‌ها ارائه داده و خطای کمتری دارند.
در انتهای این آموزش، ابزارهای آنلاینی معرفی کردیم که می‌توانید با کمک آن‌ها پاسخ‌های سریع‌تر و نسبتاً دقیق‌تری به‌دست آورید. شما می‌توانید پاسخ‌های به‌دست‌آمده از ۹ فرمول بالا را با جواب‌های ماشین‌حساب آنلاین برای انواع بیضی مقایسه کنید و دقت و خطای آن‌ها را بسنجید.
