سینوس ریاضی دهم به زبان ساده ׀ تعریف + روش محاسبه

تابع سینوس تابعی است که در محاسبات مربوط به مثلث قائم الزاویه به‌‌کار می‌‌رود و مقدار زاویه و اضلاع این نوع مثلث را به هم ربط می‌‌دهد، به همین دلیل، سینوس را یک تابع مثلثاتی می‌‌گویند. فرمول تابع سینوس صرفاً جنبه حفظی ندارد بلکه مفهومی هندسی است که لازمه درک بسیاری از مفاهیم هندسه، ریاضی، فیزیک و مهندسی است و ازاین‌‌جهت، در دنیای پیرامون ما و حل مسائل گوناگون یک تابع کاربردی محسوب می‌‌شود.

اگر به‌‌تازگی می‌‌خواهید سینوس ریاضی دهم را یاد بگیرید یا قصد مرور کردن آن را دارید، این مقاله را حتماً تا انتها دنبال کنید. در این درس‌‌نامه خواهیم آموخت که تابع سینوس در ریاضی چیست چه ویژگی‌‌هایی دارد و چگونه باید آن را برای زوایای مختلف محاسبه کرد.

تعریف سینوس فرمول ریاضی دهم

تابع «سینوس» (Sine) مانند سایر توابع مثلثاتی، بیان‌‌کننده ارتباط بین طول و زاویه است که به‌‌صورت Sin نمایش داده می‌‌شود. این تابع مثلثاتی با استفاده از مثلث قائم‌‌الزاویه و دایره مثلثاتی قابل تعریف است. اگرچه این دسته از توابع اغلب براساس مثلث قائم‌‌الزاویه معرفی می‌‌شوند، اما یادگیری آن‌‌ها براساس دایره مثلثاتی نیز در حل بسیاری از مسائل به شما کمک خواهد کرد. در ادامه، هر دو تعریف سینوس ریاضی دهم و فرمول آن را ارائه می‌‌دهیم.

تعریف سینوس با مثلث قائم الزاویه

در یک مثلث قائم‌‌الزاویه که یک زاویه حاده به‌‌نام θ دارد، سینوس زاویه (یعنی θ) از نسبت طول ضلع مقابل به طول وتر به‌‌دست می‌‌آید:

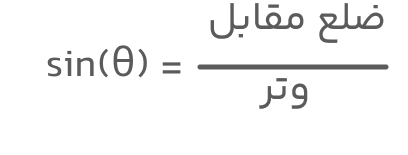
در تعریف توابع مثلثاتی ازجمله سینوس اضلاع مثلث قائم‌‌الزاویه به‌‌صورت زیر نام‌‌گذاری می‌‌شوند:

• وتر: بزرگ‌‌ترین ضلع مثلث که مقابل زاویه ۹۰ درجه قرار دارد.
• ضلع مقابل: ضلع روبه‌‌روی زاویه θ
• ضلع مجاور: ضلع مجاور زاویه θ که وتر نیست.

مثال ۱: با توجه به مثلث زیر، سینوس زاویه θ را تعیین کنید.

جواب: برای به‌‌دست آوردن سینوس زاویه θ کافی‌‌ست طول وتر را بر طول ضلع مقابل به زاویه θ تقسیم کنیم. طبق فرمول بالا و شکل داده‌‌شده خواهیم داشت:

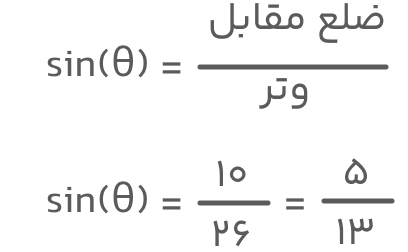
مثال ۲: در تصویر زیر یک سطح شیب‌‌دار را از کنار مشاهده می‌‌کنید که دارای شیب ۱۰ درجه و ارتفاع ۳ فوت است. طول این سطح شیب‌‌دار را به‌‌دست آورید.

جواب: سطح شیب‌‌دار همان وتر مثلث قائم‌‌الزاویه و ارتفاع ۳ فوت نیز ضلع مقابل زاویه حاده ۱۰ درجه است. بنابراین، اگر مقادیر معلوم را در فرمول سینوس قرار دهیم، می‌‌توانیم طول سطح شیب‌‌دار یعنی همان وتر را پیدا کنیم. داریم:

پس سطح شیب‌‌دار تقریباً ۱۷/۳ فوت طول دارد.

تعریف سینوس در دایره مثلثاتی

دایره مثلثاتی یا دایره واحد، دایره‌‌ای به شعاع واحد یا همان یک است که مبدأ آن در مرکز مختصات واقع شده است. توابع مثلثاتی را می‌‌توان به‌‌صورت مقادیر مختصات روی یک دایره واحد نیز تعریف کرد. با استفاده از مثلث قائم‌‌الزاویه تنها می‌‌توانستیم سینوس زوایای بین ۰ و ۹۰ درجه را حساب کنیم، اما دایره مثلثاتی امکان محاسبه سینوس تمام زاویه‌‌ها را برایمان فراهم می‌‌کند.شکل زیر یک دایره مثلثاتی را نشان می‌‌دهد.

اگر مانند تصویر زیر، روی محیط این دایره نقطه‌‌ای مثل (x,y) انتخاب کرده و یک مثلث قائم‌‌الزاویه را طوری رسم کنیم که وتر همان شعاع دایره واحد و θ نیز زاویه ایجادشده بین وتر و محور xها باشد، آنگاه طول وتر این مثلث برابر با ۱ خواهد بود و می‌‌توان فرمول سینوس ریاضی دهم را به‌‌صورت زیر نوشت:

رابطه به‌‌دست‌‌آمده این مفهوم را می‌‌رساند که مقدار y برای هر نقطه روی دایره مثلثاتی مساوی با sinθ است.

اندازه سینوس زاویه های پرکاربرد

همان‌‌طور که قبلاً هم اشاره کردیم، با استفاده از دایره مثلثاتی می‌‌توانیم مقدار سینوس را برای هر زاویه‌‌ای پیدا کنیم، اما برخی از زوایا هستند که در مثلثات بیشتر مورد استفاده قرار می‌‌گیرند. این زوایا که تعدادشان ۱۶تاست، در دایره مثلثاتی زیر برحسب درجه و رادیان نمایش داده شده‌‌اند. علاوه‌‌بر زاویه‌‌ها می‌‌توانید مختصات مربوط به هر یک از آن‌‌ها را نیز روی دایره ببینید. در این دایره مثلثاتی جهت مثبت به‌‌صورت پادساعتگرد است یعنی خلاف جهت عقربه‌‌های ساعت.

نکته: هر π رادیان معادل ۱۸۰ درجه است.

اگر جهت چرخش در دایره مثلثاتی در جهت منفی یعنی به‌‌صورت ساعتگرد (در جهت عقربه‌‌های ساعت) باشد، آنگاه زاویه منفی خواهد بود. برای مثال، اگر از صفر درجه شروع کنیم و به‌‌اندازه ۳۰ درجه چرخش پادساعتگرد داشته باشیم زاویه را همان ۳۰ درجه نشان می‌‌دهیم، اما اگر در جهت منفی، ۳۰ درجه پیش برویم، آنگاه زاویه منفی بوده و آن را با ۳۰- درجه نشان می‌‌دهیم. بنابراین، زاویه‌‌ای که علامت منفی دارد نشان‌‌دهنده حرکت ساعتگرد یا چرخش در جهت منفی دایره مثلثاتی خواهد بود.

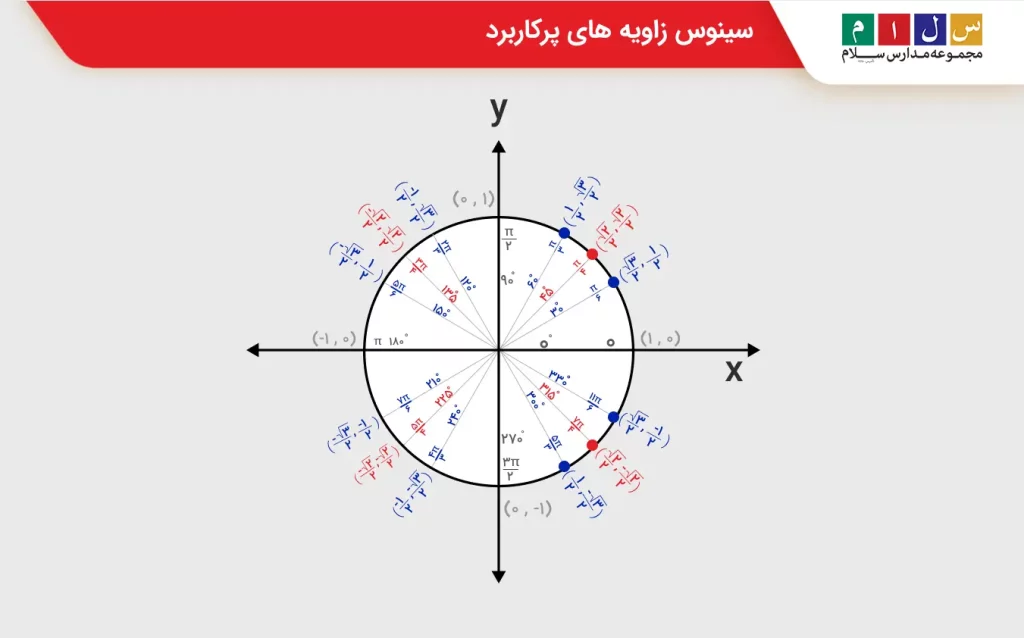
در شکل بالا، مقدار x در هر کدام از مختصات نشان‌‌دهنده کسینوس آن زاویه و مقدار y نیز نشان‌‌دهنده سینوس آن است. به‌‌عنوان مثال، با توجه به مختصات دایره، مقدار سینوس برای زاویه ۰ درجه برابر با ۰ و برای زاویه ۹۰ درجه برابر با ۱ است. الگوی تغییر مقدار سینوس در ربع اول برعکس الگوی تغییر کسینوس است، زیرا در این ناحیه با افزایش مقدار زاویه، مقدار سینوس نیز افزایش می‌‌یابد درحالی که مقدار کسینوس الگوی کاهشی دارد. در جدول زیر، روند افزایشی مقدار سینوس در ربع اول به‌‌خوبی دیده می‌‌شود.

پیشنهاد: کسینوس چیست؟

ازآنجا که مقدار y در هر نقطه از محیط دایره مثلثاتی نشان‌‌دهنده سینوس است و مقادیر y در ربع اول و دوم مثبت و در ربع سوم و چهارم منفی است، می‌‌توان نتیجه گرفت که مقدار سینوس تنها در ربع اول و دوم مثبت است و در ربع سوم و چهارم مقداری منفی دارد.
با توجه به اینکه برخی از زاویه‌‌ها در حل مسائل گوناگون بیشتر مورد استفاده قرار می‌‌گیرند، بهتر است مقادیر سینوس آن‌‌ها را به ذهن خود بسپارید. جدول زیر می‌‌تواند در یادسپاری سینوس زاویه‌‌های پرکاربرد به شما کمک کند.

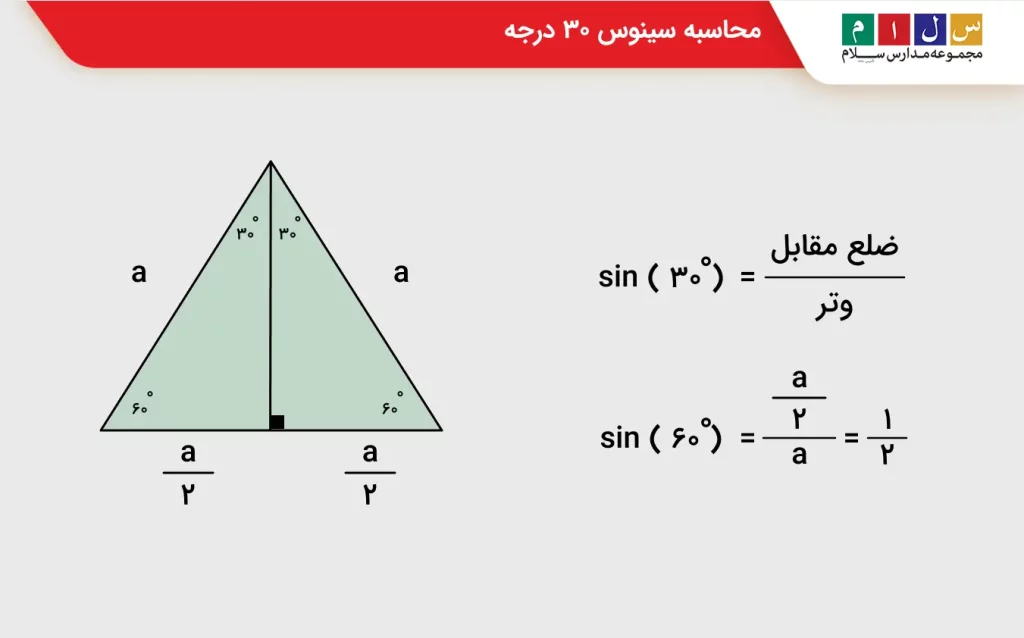
روش محاسبه سینوس ۳۰ درجه

اکنون که با دایره مثلثاتی و تعریف سینوس آشنا شدیم، می‌‌دانیم که مقدار سینوس زاویه ۳۰ درجه برابر با یک‌‌دوم است. اما این مقدار را چگونه می‌‌توان به‌‌دست آورد. در اینجا روشی را معرفی می‌‌کنیم که با کمک آن بتوانید به‌‌راحتی اثبات کنید که مقدار سینوس ۳۰ درجه مساوی یک‌‌دوم است.

برای این کار، ابتدا یک مثلث متساوی الاضلاع در نظر می‌‌گیریم. این مثلث را به این دلیل انتخاب می‌‌کنیم که سه ضلع مساوی و سه زاویه برابر با ۶۰ درجه دارد. مطابق تصویر زیر، از یکی از رأس‌‌ها خطی عمود رسم کرده و مثلث را به دو قسمت مساوی تقسیم می‌‌کنیم.
همان‌‌گونه که در آموزش‌‌های پیشین آموختیم، در یک مثلث متساوی‌‌الاضلاع نیمساز، ارتفاع، میانه و عمودمنصف روی هم منطبق می‌‌شوند و مثلث را به دو نیمه مساوی تقسیم می‌‌کنند. بنابراین، خط عمودی که رسم کرده‌‌ایم، نیمساز و عمودمنصف نیز هست، یعنی زاویه ۶۰ درجه را به دو زاویه ۳۰ درجه و ضلع مقابل را به دو نیمه مساوی تقسیم می‌‌کند. حالا دو مثلث قائم‌‌الزاویه داریم و می‌‌توانیم با فرمولی که در ابتدا ارائه کردیم سینوس ۳۰ درجه را محاسبه کنیم. داریم:

به همین راحتی مقدار sin ۳۰° محاسبه شد.

زاویه مرجع در مثلثات

 زاویه حاده‌‌ای که از آن برای نمایش زاویه‌‌های مختلف استفاده می‌‌شود، زاویه مرجع نام دارد. برای هر زاویه‌‌ای که در صفحه مختصات وجود دارد، می‌‌توان یک زاویه مرجع که اندازه آن بین ۰ تا ۹۰ درجه است، در نظر گرفت. در شکل زیر، زاویه دلخواه θ و زاویه مرجع آن یعنی ‘θ نشان داده شده است.

به‌‌دلیل اینکه ‘θ زاویه مرجع θ است، ‘ sin θ و sin θ دارای مقدار یکسانی خواهند بود. به‌‌عنوان مثال، ˚۳۰ زاویه مرجع ˚۲۱۰ است و با مراجعه به دایره مثلثاتی خواهیم دید که بزرگی مقدار سینوس هر دوی آن‌‌ها برابر با یک‌‌دوم است. البته چون زاویه ۲۱۰ درجه در ربع سوم دایره واحد قرار می‌‌گیرد، مقدار سینوس آن علامت منفی نیز دارد.

به‌‌طور کلی، بزرگی مقدار سینوس تمام زوایایی که زاویه مرجعشان ˚۳۰ است برابر با یک‌‌دوم خواهد بود. تنها تفاوتی که ممکن است بینشان وجود داشته باشد علامت مقدار سینوس آن‌‌ها است که با توجه به محل قرارگیری ضلع دوم زاویه در هر یک از چهار ربع دایره مثلثاتی می‌‌توان آن را مشخص کرد (ضلع اول زاویه در امتداد و در جهت محور xهاست). اگر یک زاویه معین مثل θ داشته باشیم، زاویه مرجع آن را طبق مراحل زیر تعیین می‌‌کنیم:

1. درصورتی که زاویه θ بزرگ‌‌تر از ˚۳۶۰ (۲π) باشد، تا جای ممکن و به تعداد کافی مقدار ˚۳۶۰ (۲π) را از زاویه θ کم می‌‌کنیم. دقت داشته باشید که این کار را تا جایی انجام می‌‌دهیم که حاصل تفریق بین ۰ تا ˚۳۶۰ یا ۰ تا ۲π باشد. اگر زاویه حاصل بین ۰ تا ˚۹۰ باشد آن زاویه، زاویه مرجع خواهد بود.
2. در مرحله بعدی، به ضلع دوم زاویه نگاه می‌‌کنیم که در کدام ربع دایره واقع شده است.
3. پس از مشخص شدن محل قرارگیری ضلع دوم زاویه می‌‌توانیم از معادله‌‌هایی که در تصویر زیر نشان داده شده‌‌اند برای تعیین زاویه مرجع استفاده کنیم.

نکته: در ربع اول’θ = θ است.

مثال ۱: سینوس ˚۱۲۰ را بیابید.
جواب: ازآنجا که زاویه ˚۱۲۰ بین ۰ و ˚۳۶۰ قرار دارد، لازم نیست که ˚۳۶۰ را از آن کم کنیم. واضح است که زاویه ˚۱۲۰ در ربع دوم قرار دارد. این بدین معنی است که علامت مقدار سینوس این زاویه مثبت است.
حالا با کمک معادله‌‌ای که در تصویر بالا برای تعیین زاویه مرجع ارائه شده است، زاویه مرجع این زاویه را حساب می‌‌کنیم:

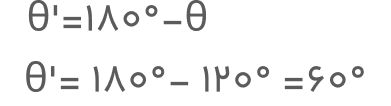
زاویه مرجع برابر با ˚۶۰ است. پس مقدار سینوس ˚۱۲۰ به‌‌صورت زیر خواهد بود:

مثال ۲: مقدار سینوس زاویه ˚۶۹۰ را تعیین کنید.
جواب: این زاویه از ۳۶۰ بیشتر است. پس ابتدا باید تا جایی که امکان دارد مقدار ˚۳۶۰ را از آن کم کنیم.

۶۹۰° – ۳۶۰° =۳۳۰°

زاویه ˚۳۳۰ در ربع چهارم قرار می‌‌گیرد. بنابراین، می‌‌توانیم از فرمول زیر زاویه مرجع را به‌‌دست آوریم:

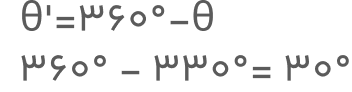
سینوس زاویه مرجع یعنی ˚۳۰ برابر با یک‌‌دوم است، اما چون زاویه ˚۳۳۰ در ربع چهارم قرار دارد، مقدار سینوس این زاویه منفی خواهد بود.

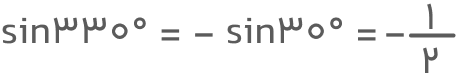
ویژگی های تابع سینوس چیست؟

تابع سینوس مانند سایر توابع در ریاضی دارای یک‌‌سری خواص است که لازم است با آن‌‌ها آشنا شوید. در ادامه ویژگی‌‌های این تابع را بیان می‌‌کنیم.

• سینوس تابعی فرد است. در ریاضی تابع f را فرد می‌‌گویند اگر باشد. نمودار چنین تابعی نسبت به مبدأ مختصات تقارن دارد. طبق این تعریف خواهیم داشت:

مثال:

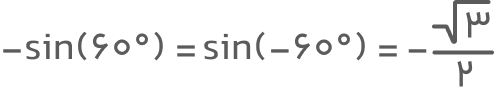
• دامنه تابع سینوس مجموعه تمام اعداد حقیقی و برد آن است. مقادیر ورودی تابع سینوس مجموعه اعداد حقیقی و مقادیر خروجی آن در بازه قرار دارد.

• سینوس تابعی متناوب است. منظور از متناوب بودن تابع سینوس، تکرار شدن مقدار سینوس پس از هر دور کامل به‌‌اندازه ۲π است. این یعنی اینکه دوره تناوب تابع سینوس ۲π است. نموداری که در تصویر زیر می‌‌بینید، گویای متناوب بودن این تابع است.

برای چندین دور کامل، این رابطه به‌‌صورت زیر نوشته می‌‌شود:

n یک عدد صحیح است.

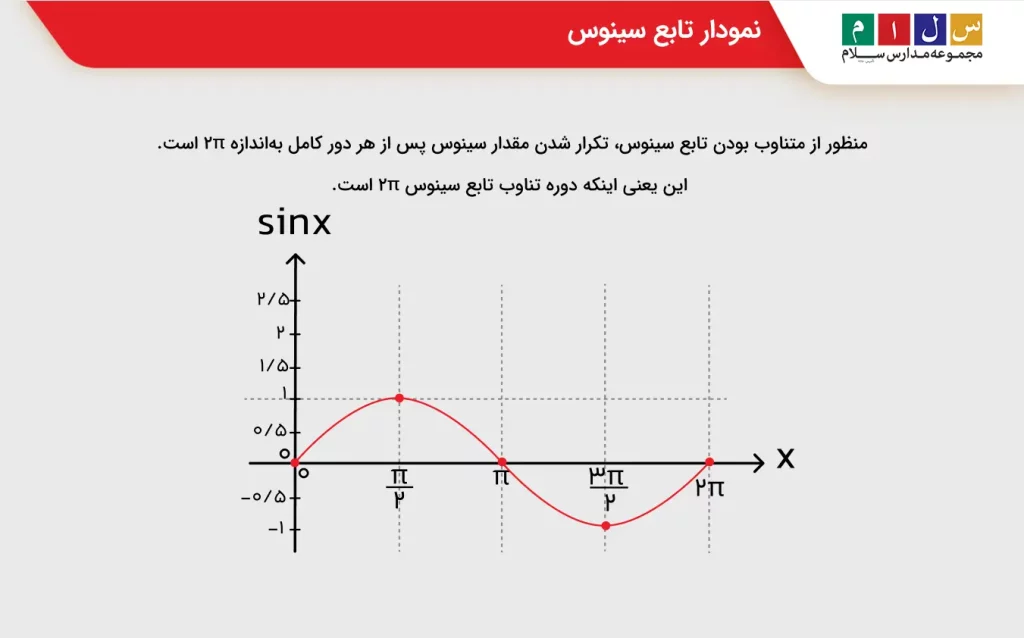
برای درک بهتر، شکل زیر را در نظر بگیرید. طبق این شکل با اضافه کردن ۲π به مقدار سینوس تغییری نمی‌‌کند. این عدم تغییر به‌‌دلیل متناوب بودن تابع سینوس پس از هر دور کامل است.  

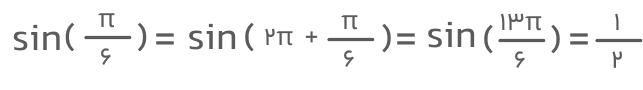
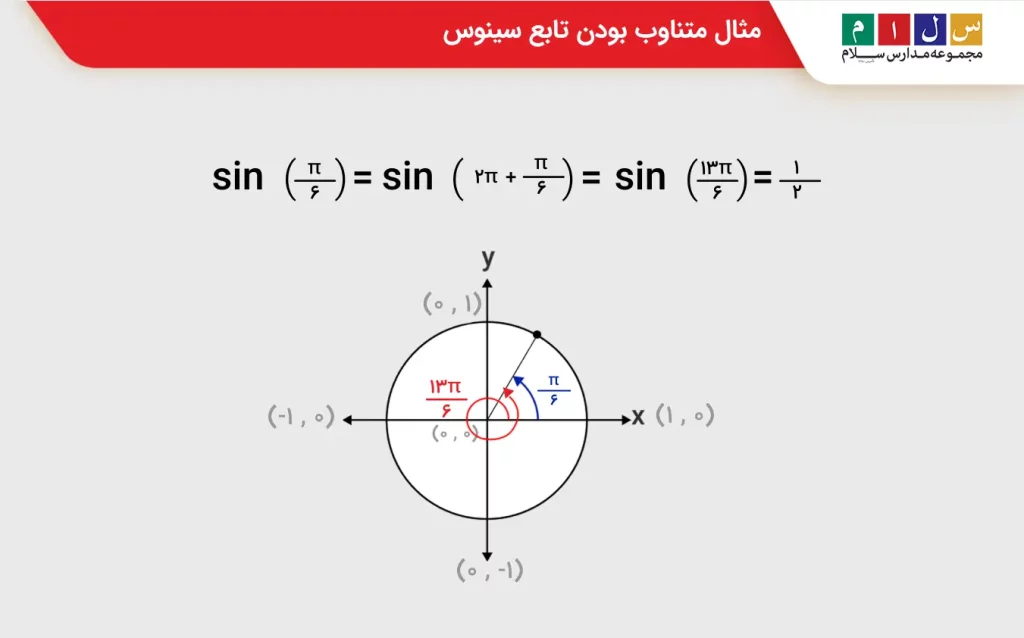
مثال‌‌های زیر نمونه‌‌ای از کاربرد تناوبی بودن تابع سینوس هستند:

وارون تابع سینوس

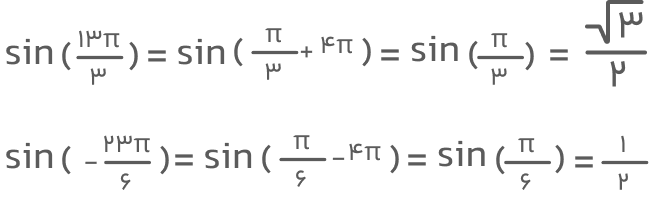
پس از آشنایی با تابع سینوس مثلثات دهم، نوبت معرفی وارون این تابع است. وارون تابع سینوس را به‌‌صورت یا arcsinx نشان می‌‌دهند و آن را «آرک سینوس» می‌‌نامند. وارون سینوس به‌‌شکل زیر بیان می‌‌شود:

sin (x) = y

sin^-۱ (y) = x

دامنه آرک سینوس مشابه برد تابع سینوس یعنی  و برد آن نیز مجموعه اعداد حقیقی متعلق به بازه است.

مثال: ( sin^-۱ (-۱ را به‌‌دست آورید.

جواب: طبق رابطه وارون تابع سینوس، می‌‌توانیم این مقدار را تعیین کنیم:

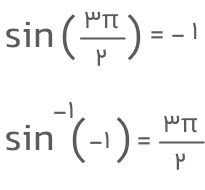
نکته: اگر تابع سینوس در مخرج کسر قرار گیرد و صورت کسر هم برابر با ۱ باشد، آنگاه تابعی به‌‌نام «کسکانت» (cosecant) خواهیم داشت:

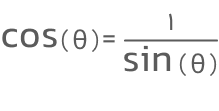
سخن پایانی

در این آموزش آموختیم که سینوس در ریاضی چیست و از چه فرمولی به‌‌دست می‌‌آید. مبحث مثلثات بسیار گسترده است و ما در اینجا سعی کردیم با مثال‌‌های حل‌‌شده و نمودارهایی که ارائه دادیم، ویژگی‌‌های تابع سینوس ریاضی دهم را به‌‌صورت کلی معرفی کنیم. بدون شک برای شناخت بیشتر تابع سینوس، مطالعه این مقاله به‌‌تنهایی کافی نیست. حل تمرین‌‌های کاربردی در این زمینه می‌‌تواند شما را در درک بهتر این تابع مثلثاتی یاری کند.