فهرست مطالب
Toggleاتحادها در ریاضی مجموعهای مهم از تساویها هستند که بهازای هر مقداری برقرار هستند. این تساویها پایه و اساس جبر را تشکیل میدهند و برای سادهسازی محاسبات مورد استفاده قرار میگیرند. پاسخ دادن به برخی از مسائل جبری، نیاز به طی کردن مراحل متعددی دارد، اما اتحادها به ما کمک میکنند تا بدون هیچ مرحله اضافی محاسبات را بهراحتی انجام دهیم. ما در مقالات قبلی درباره اتحاد چاق و لاغر و اتحاد مزدوج صحبت کردهایم.
اتحاد مربع از پرکاربردترین و سادهترین اتحادهای ریاضی است که در اینجا قرار است شما را با آن آشنا کنیم. ابتدا اتحاد مربع و انواع آن را تعریف و اثبات میکنیم، سپس به حل چند نمونه سؤال از اتحاد مربع سهجملهای و اتحاد مربع دو جمله ای نهم میپردازیم. اگر قصد یادگیری کامل این مبحث را دارید، توصیه میکنیم این آموزش از مجموعه مدارس سلام را تا انتها دنبال کنید.
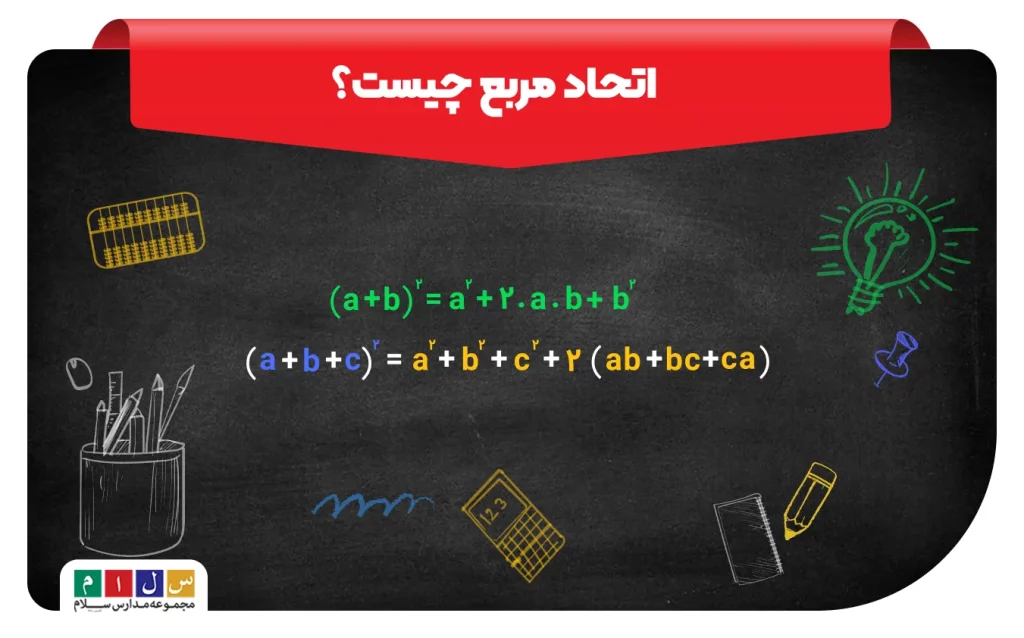
اتحاد مربع چیست؟
منظور از اتحاد مربع به توان ۲ رسیدن مجموع یا تفاضل دو جمله، سه جمله و… است. البته در ریاضی اتحاد مربع دوجملهای و سهجملهای نسبت به چندجملهایهای دیگر، اتحادهای مربع متداولتری هستند که در بخشهای بعدی با آنها آشنا خواهیم شد.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
اتحاد مربع دو جمله ای
اتحاد مربع دوجملهای به اتحادی گفته میشود که در آن مجموع یا تفاضل دو جمله به توان ۲ برسد. در ادامه فرمول هر یک از این دو حالت را بیان میکنیم و به توضیح اتحاد دو جمله ای بیشتر میپردازیم.
اتحاد مربع دو جمله ای مجموع
اگر مجموع دو جمله a و b به توان ۲ برسد، اتحاد مربع دوجملهای بهصورت زیر خواهد بود:
(a + b)۲= a۲ + ۲ab + b۲
این تساوی که به آن اتحاد نوع اول نیز میگوییم، بهازای هر مقدار a و b برقرار است.
اتحاد مربع دو جمله ای تفاضل
اتحاد مربع تفاضل دو جمله که اتحاد نوع دوم نیز نامیده میشود، مشابه اتحاد نوع اول است با این تفاوت که بین دو جمله بهجای علامت جمع، علامت منها قرار دارد. فرمول این اتحاد بهصورت زیر است:
a – b)۲= a۲– ۲ab + b۲)
اثبات فرمول اتحاد مربع دو جمله ای
از آموزش اعداد توان دار به یاد داریم جملهای که به توان دو میرسد یعنی دو بار در خودش ضرب میشود. طبق این گفته میتوان دو اتحاد بالا را بهراحتی اثبات کرد. کافیست از عبارت سمت چپ شروع کنیم و آن را بهصورت زیر بنویسیم:
a + b)۲ = (a + b) (a + b))
a – b)۲ = (a – b) (a – b))
حالا عبارتهای سادهشده را در هم ضرب میکنیم:
- اثبات اتحاد نوع اول:
a + b)۲ = (a + b) (a + b))
(a(a + b) + b(a + b =
a۲ + ab + ba + b۲ =
a۲ + ۲ab + b۲ =
- اثبات اتحاد نوع دوم:
a – b)۲ = (a – b) (a – b))
(a(a – b) – b(a – b =
a۲– ab – ba + b۲ =
a۲ – ۲ab + b۲ =
همانطور که دیدید، در هر دو حالت به طرف دوم اتحاد رسیدیم و تساویها بهآسانی اثبات شد.
اثبات هندسی اتحاد مربع دو جمله ای
اثبات اتحاد مربع دوجملهای با رسم شکل نیز امکانپذیر است. ابتدا اتحاد نوع اول را با این روش اثبات میکنیم. یک مربع به ضلع (a+b) مانند شکل زیر در نظر بگیرید. میدانیم که مساحت مربع برابر با اندازه یک ضلع به توان دو است، پس مساحت این مربع مساوی با مقدار زیر خواهد بود:
a + b)2)
ازطرفی، این مربع شامل چهار قسمت با مساحتهای گوناگون است که در تصویر زیر مقدار آنها مشخص است. مجموع مساحت این چهار قسمت برابر است با
a۲ + ab + ba + b۲ = a۲ + ۲ab + b۲
واضح است که مجموع مساحت این چهار بخش برابر با مساحت مربع بزرگ است. پس خواهیم داشت:
a + b)۲ = a۲ + ۲ab + b۲)
اتحاد نوع اول را اثبات کردیم. حالا نوبت اثبات اتحاد نوع دوم است. اثبات هندسی اتحاد مربع تفاضل دو جمله با اندکی تفاوت مانند اتحاد مربع مجموع دو جمله انجام میشود.
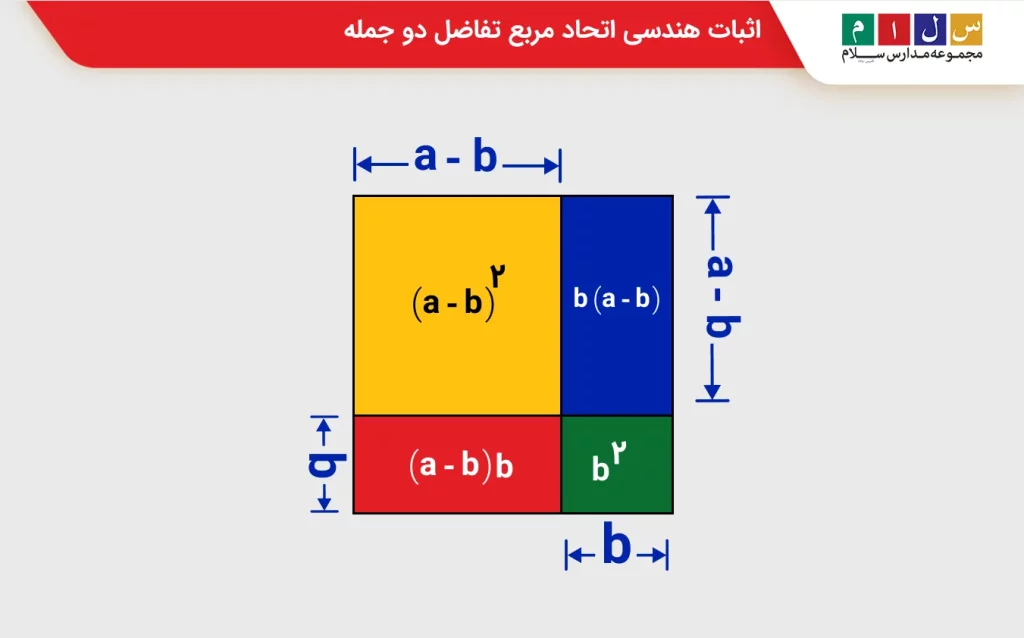
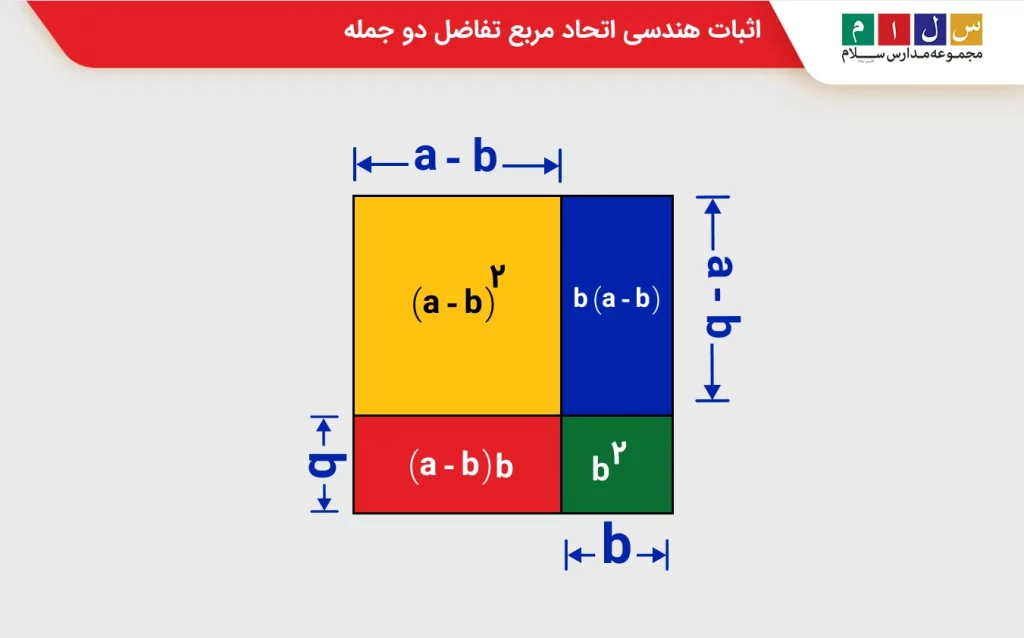
مربعی به ضلع a در نظر بگیرید که هر چهار ضلع آن مانند شکل زیر به دو قسمت با اندازه a-b و b تقسیم شده است. مساحت این مربع برابر است با a۲. با توجه به اینکه اضلاع مربع را به دو قسمت تقسیم کردهایم، میتوانیم مساحت شکل را به چهار قسمت تقسیم کنیم. مجموع مساحت این چهار شکل مساوی با مساحت مربع بزرگ است. بنابراین، با توجه به شکل زیر، تساوی زیر را میتوانیم بنویسیم:
a۲ = (a – b)۲ + b(a – b) + (a – b)b + b۲
a۲ = (a – b)۲+ ba – b۲ + ab – b ۲+ b۲
a۲ = (a – b)۲ + ۲ab – b۲
a۲ – ۲ab + b۲ = (a – b)۲
برای اینکه با اتحاد مربع بیشتر آشنا شوید، در ادامه چند نمونه اتحاد مربع دو جمله ای با جواب آوردهایم.
نمونه سوال تجزیه اتحاد مربع دو جمله ای
عبارت زیر را تجزیه کنید.
x۲ – ۱۰x + ۲۵
جواب: عبارت دادهشده شبیه به اتحاد مربع است. میتوانیم آن را بهصورت زیر بنویسیم:
x۲ – ۲(۵x) + (۵)۲
اگر این عبارت را با فرمول اتحاد مربع تفاضل دو جمله مقایسه کنیم، خواهیم داشت:
a۲– ۲(ab) + b۲
x۲– ۲(۵x) + ۵۲
- a=x
- b=۵
x۲– ۲(۵x) + ۵۲ = (x – ۵) ۲
نمونه سوال اتحاد مربع دو جمله ای
اگر x – y = ۴ و xy=۱۲ باشد، مقدار x۲ + y۲ چقدر است؟
جواب: از اتحاد مربع تفاضل دو جمله زیر استفاده میکنیم و مقادیر دادهشده را در آن قرار میدهیم:
x – y)۲= x۲– ۲xy + y۲)
(۴)۲ = x۲ – ۲(۱۲) + y۲
اکنون میتوانیم مقدار x۲ + y۲ را بهدست آوریم:
x۲ + y۲ = (۴)۲ + ۲ (۱۲) = ۱۶ + ۲۴ = ۴۰
نمونه سوال اتحاد مربع دو جمله ای کسری
جواب: از رابطه اتحاد مربع کمک میگیریم. ابتدا فرمول اتحاد مربع مجموع دو جمله 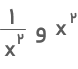
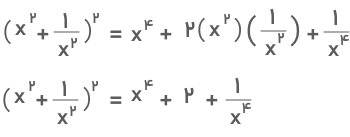
با جایگذاری مقدار دادهشده، حاصل بهدست میآید:
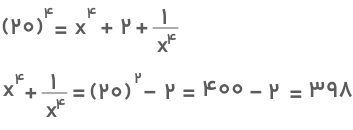
پیشنهاد مطالعه: کسر چیست ؟ + معرفی انواع کسر
اتحاد مربع سه جمله ای
منظور از اتحاد مربع سهجملهای اتحادی است که در آن مجموع یا تفاضل سه جمله به توان ۲ برسد. در ادامه این آموزش، درمورد این نوع اتحاد مربع بیشتر صحبت میکنیم و به اثبات آن میپردازیم.
اتحاد مربع سه جمله ای مجموع
اگر سه جمله a، b و c داشته باشیم، اتحاد مربع مجموع آنها بهصورت زیر بیان خواهد شد:
a + b + c)۲ = a۲ + b۲ + c۲ + ۲(ab + bc + ca ))
اتحاد مربع سه جمله ای تفاضل
این نوع اتحاد که بین سه جمله آن علامت منها وجود دارد بهصورت زیر است:
a – b – c)۲ = a۲ + b۲ + c۲ – ۲ab + ۲bc – ۲ca)
اثبات فرمول اتحاد مربع سه جمله ای
اثبات فرمولهای اتحاد مربع سهجملهای کار سادهای است. کافیست عبارتهای سمت چپ را سادهتر کنیم تا به عبارتهای سمت راست برسیم.

- اثبات اتحاد مربع مجموع سه جمله:
a + b + c)۲ = (a + b + c) (a + b + c))
=a۲+ ab + ac + ba + b۲+ bc + ca + cb + c۲
=a۲ + b۲ + c۲ + ۲ab + ۲bc + ۲ca
=a۲+b۲+c۲+ ۲(ab + bc + ca)
- اثبات اتحاد مربع تفاضل سه جمله:
a – b – c)۲= (a – b – c) (a – b – c))
=a۲– ab – ac – ba + b۲+ bc – ca + cb + c۲
=a۲ + b۲+ c۲ -۲ab + ۲bc -۲ca
اگر علاقهمند به اثبات هندسی این اتحادها هستید، میتوانید مانند اتحادهای مربع دوجملهای با رسم یک مربع و تقسیم کردن آن به شکلهای کوچکتر، این کار را انجام دهید.
پیشنهاد مطالعه: اتحاد جمله مشترک چیست؟
چند نمونه سوال اتحاد مربع با جواب
در این بخش، چند مثال برای اتحاد مربع دو جمله ای و سهجملهای حل میکنیم تا هم با کاربرد اتحاد مربع در حل مسائل گوناگون آشنا شوید و هم این مبحث بهتر در خاطرتان بماند.
سؤال ۱: با استفاده از اتحادها عبارت زیر را ساده کنید.
۵p – ۶q)۲ + (۵p + ۶q)۲)
جواب: ابتدا هر دو جمله این عبارت را با کمک اتحاد مربع دوجملهای بسط میدهیم:
۵p – ۶q)۲ =(۵p)۲ – ۲(۵p) (۶q) + (۶q)۲ =۲۵p۲ – ۶۰pq + ۳۶q۲)
۵p + ۶q)۲=(۵p)۲ + ۲(۵p)(۶q) + (۶q)۲=۲۵p۲ + ۶۰pq + ۳۶q۲)
حالا تساویها را با هم جمع میکنیم:
۵p – ۶q)۲+ (۵p + ۶q)۲ = ۲۵p۲ – ۶۰pq + ۳۶q۲ + ۲۵p۲ + ۶۰pq + ۳۶q۲)
=۵۰p۲ + ۷۲q۲
سؤال ۲: اگر a+b=۱۲ و ab=۳۵ باشد، a۴+b۴ چقدر است؟
جواب: a۴+b۴ را میتوانیم بهصورت 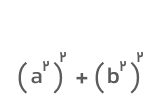
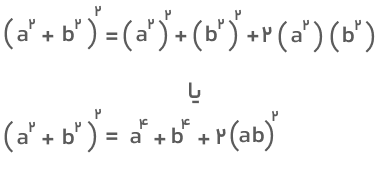
ازطرفی، مقدار a۲+b۲ را میتوانیم از رابطه زیر تعیین کنیم:
a+b)۲ = a۲ + b۲ + ۲ab)
a۲+b۲ = (a+b)۲ – ۲ab
با جایگذاری مقادیر دادهشده داریم:
a۲ + b۲= (a+b)۲ – ۲ab = ۱۲۲– ۲(۳۵) = ۱۴۴ – ۷۰ = ۷۴
اکنون مقدار بهدستآمده را در تساوی اول قرار میدهیم تا حاصل a۴+b۴ تعیین شود:
a۲ + b۲)۲ =a۴+ b۴ + ۲(ab)۲)
(۷۴)۲ = a۴ + b۴ + ۲(۳۵)۲
a۴+ b۴= (۷۴)۲ – ۲(۳۵)۲ = ۵۴۷۶ – ۲۴۵۰ = ۳۰۲۶
سؤال ۳: با کمک اتحاد مربع مقدار ۵۸۲ را بهدست آورید.
جواب: مقدار این عدد را هم میتوان با استفاده از اتحاد مربع نوع اول و هم با استفاده از اتحاد مربع نوع دوم محاسبه کنیم. اگر از اتحاد مربع نوع اول استفاده کنیم، داریم:
۵۸۲ = (۵۰+۸)۲= ۵۰۲ + ۸۲+ ۲(۵۰) (۸) =۲۵۰۰ + ۶۴ + ۸۰۰= ۳۳۶۴
با کمک اتحاد مربع نوع دوم نیز به همین جواب خواهیم رسید:
۵۸۲= (۶۰ – ۲)۲ = ۶۰۲ + ۲۲ – ۲(۶۰)(۲) = ۳۶۰۰ + ۴ -۲۴۰= ۳۳۶۴
سؤال ۴: اگر تساویهای زیر برقرار باشد، مقدار a۲+b۲+c۲ چقدر خواهد بود؟
a + b + c =۱۶
ab + bc + ca = ۸۱
جواب: برای رسیدن به پاسخ، اتحاد مربع سهجملهای را بهکار میبریم و مقادیر معلوم را در آن جایگذاری میکنیم:
a + b + c)۲ = a۲+ b۲ + c۲ + ۲(ab + bc + ca))
(۱۶)۲ = a۲ + b۲+ c۲ + ۲(۸۱)
a۲ + b۲ + c۲ = (۱۶)۲ – ۲(۸۱) = ۲۵۶ – ۱۶۲ =۹۴
سؤال ۵: تساویهای زیر را داریم:
a۲+ b۲ + c۲ = ۷۷
ab – bc + ca = ۳۴
مقدار a-b-c را محاسبه کنید.
جواب: برای محاسبه این عبارت کافیست از اتحاد مربع تفاضل سهجملهای استفاده کنیم:
a – b – c)۲= a۲ + b۲ + c۲ – ۲ab + ۲bc – ۲ca)
a – b – c)۲ = a۲ + b۲ + c۲ – ۲(ab – bc + ca))
a – b – c)۲ = ۷۷ – ۲(۳۴) = ۷۷ – ۶۸ = ۹)
a – b – c = ۳
سخن پایانی
در این مطلب اتحاد مربع دوجملهای و سهجملهای را آموزش دادیم و آنها را به روشهای مختلف اثبات کردیم. همچنین، برای یادگیری عمیقتر اتحاد مربع سهجملهای و اتحاد مربع دو جمله ای مثال های متعددی حل کردیم. در پایان این مقاله خوب است این نکته را یادآور شویم که یادگیری اتحادها و ثبت آنها در حافظه نیازمند تمرین و تکرار است که این مورد با حل تمرینهای گوناگون قابل دستیابی است.