اتحاد مکعب چیست؟ | فرمول و اثبات اتحاد مکعب + مثال

گاهی اوقات در حل مسائل ریاضی به‌‌خصوص مسائل جبری با عبارت‌‌هایی روبه‌‌رو می‌‌شویم که نمی‌‌توانیم خیلی سریع پاسخ آن‌‌ها را به‌‌دست آوریم. چنین مسائلی معمولاً پیچیده به نظر می‌‌رسند و برای حل آن‌‌ها باید از راهکار‌‌های دیگری استفاده کرد.

در اینگونه مواقع این اتحادها هستند که می‌‌توانند به کمک ما بیایند و مسائل را برایمان ساده‌‌تر کنند. یکی از اتحادهایی که می‌‌تواند در این زمینه به ما کمک کند، اتحاد مکعب است که در این آموزش سایت سلام طریقه استفاده از آن را به‌‌طور کامل به شما خواهیم آموخت. پس با ما همراه باشید.

اتحاد مکعب دو جمله ای

منظور از واژه مکعب، توان ۳ است. بنابراین، وقتی می‌‌گوییم اتحاد مکعب دوجمله‌‌ای یعنی اتحادی که در آن مجموع یا تفاضل دو جمله به توان ۳ رسیده است. در بخش بعدی، فرمول اتحاد مکعب دوجمله‌‌ای را زمانی که علامت بین دو جمله + یا – است، بیان خواهیم کرد.

اتحاد مکعب مجموع دو جمله

اتحاد مکعب مجموع دو جمله از مجموع دو جمله به توان ۳ به دست می‌‌آید. اگر دو جمله a و b داشته باشیم و مجموع آن‌‌ها را به توان ۳ برسانیم تساوی زیر برقرار خواهد بود. این تساوی همان اتحاد مکعب مجموع دو جمله است.

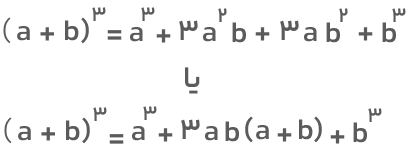
اتحاد مکعب تفاضل دو جمله

اتحاد مکعب تفاضل تاحدودی شبیه اتحاد مکعب مجموع است و تنها در علامت بین جمله‌‌ها با آن فرق دارد. منظور از اتحاد مکعب تفاضل دو جمله این است که اگر دو جمله مانند a و b داشته باشیم و تفاضل آن‌‌ها را به توان ۳ برسانیم، تساوی زیر برقرار خواهد بود. این تساوی همان اتحاد مکعب تفاضل دو جمله است.

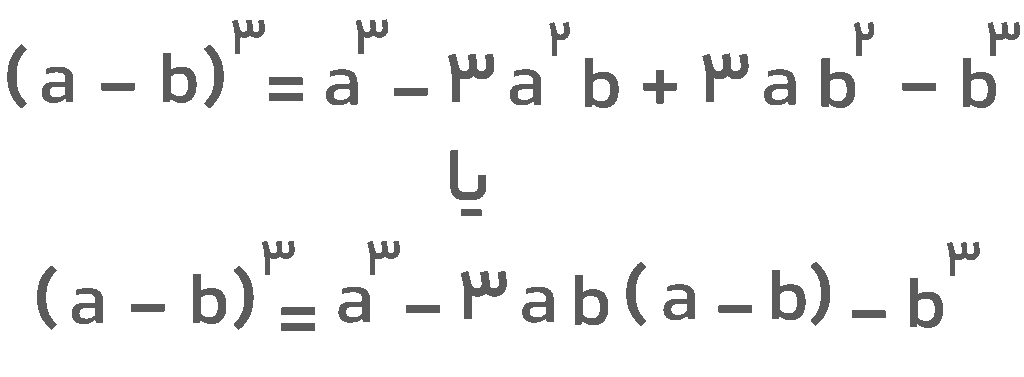
خوب است در اینجا نکته‌‌ای را یادآور شویم. بسیاری از دانش‌‌آموزان اتحادهای مکعب دوجمله‌‌ای را با اتحادهای چاق و لاغر اشتباه می‌‌گیرند. این اتحادها به‌‌صورت زیر هستند:

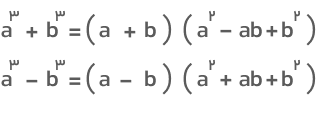
اگر دقت کنید می‌‌بینید که این اتحادها و اتحادهای مکعب دوجمله‌‌ای کاملاً با هم فرق دارند و تنها شباهت آن‌‌ها توان ۳ است که شما را به اشتباه می‌‌اندازد. پس در محاسبات حتماً این تفاوت‌‌ها را مد نظر داشته باشید.

اثبات اتحاد مکعب دو جمله ای

اثبات اتحادهای مکعب دوجمله‌‌ای کار بسیار ساده‌‌ای است. تنها کاری که لازم است انجام دهید این است که عبارت سمت چپ اتحادها را به‌‌صورت زیر بنویسید:

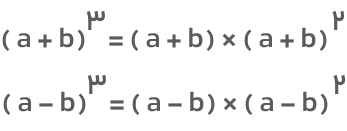
جمله‌‌های همان اتحاد مربع هستند که به‌‌صورت زیر می‌‌توان آن‌‌ها را نوشت:

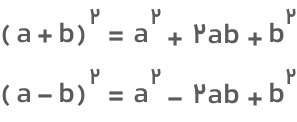
اکنون می‌‌توانیم عبارت سمت چپ اتحاد مکعب را به‌‌شکل زیر بنویسیم و جملات را در هم ضرب کنیم:

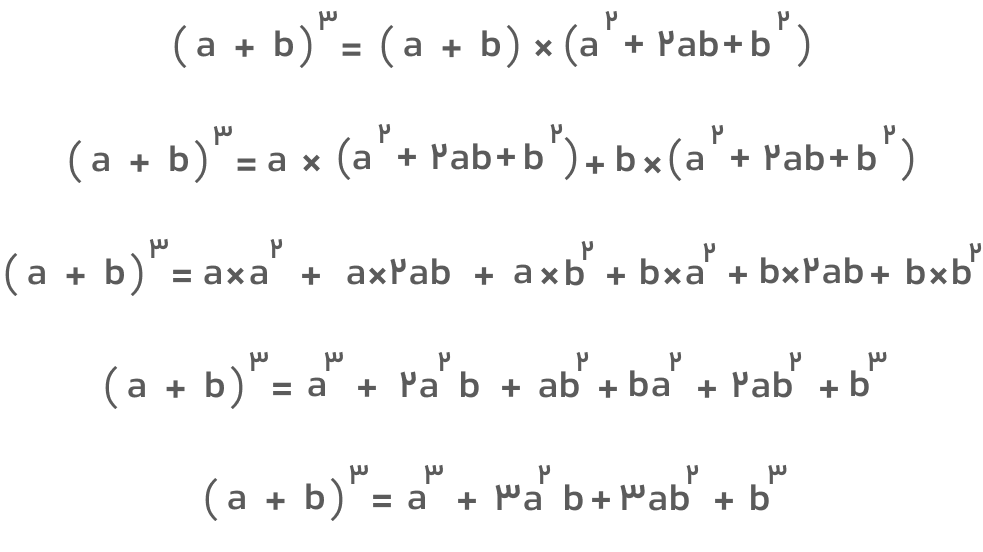
عبارت به‌‌دست‌‌آمده همان اتحاد مکعب مجموع دو جمله است. در کنار این اثبات، مشاهده شکل زیر که تعبیر هندسی این اتحاد را نشان می‌‌دهد، می‌‌تواند درک خوبی از اتحاد مکعب مجموع دو جمله به شما بدهد.

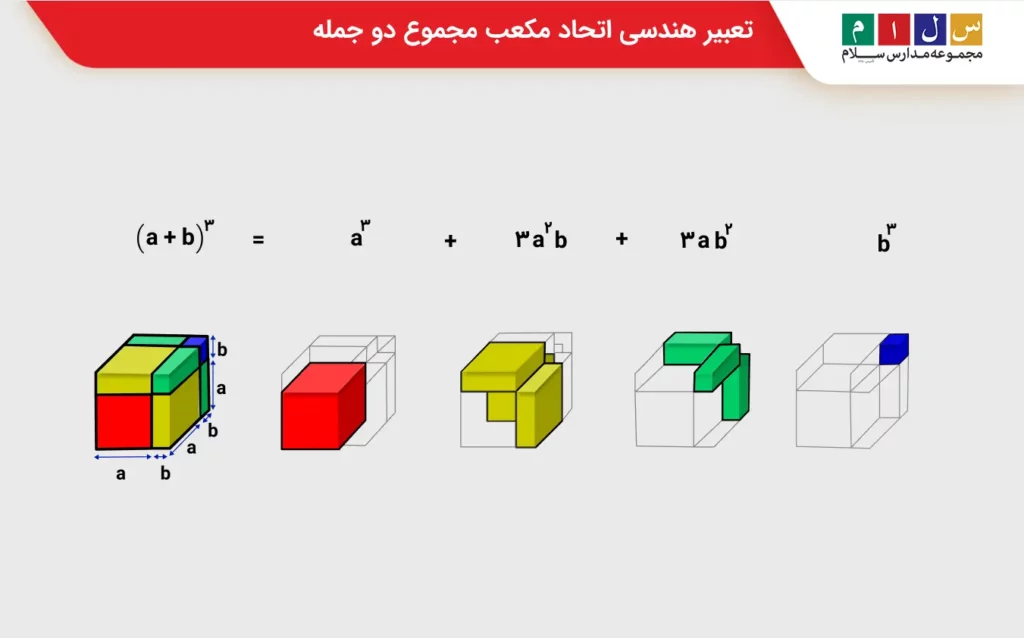
برای اثبات اتحاد مکعب تفاضل دو جمله نیز روش مشابهی را در پیش می‌‌گیریم. خواهیم داشت:

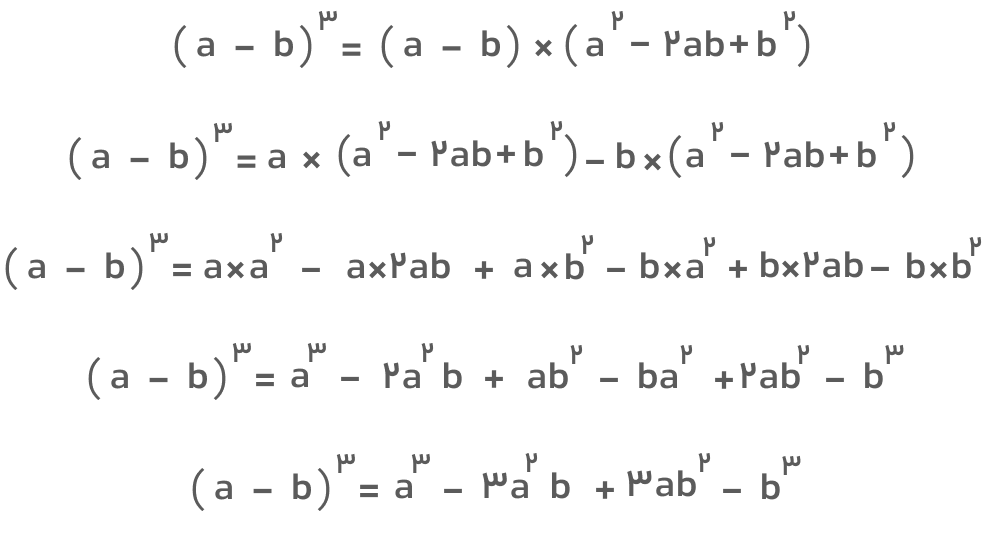
اتحاد مکعب سه جمله ای

اتحاد مکعب مجموع سه جمله یکی دیگر از انواع اتحاد مکعب است که در این بخش به آن می‌‌پردازیم. این اتحاد به‌‌صورت توان سوم مجموع سه جمله بیان می‌‌شود و فرمول آن برای سه جمله a، b و c به‌‌شکل زیر است:

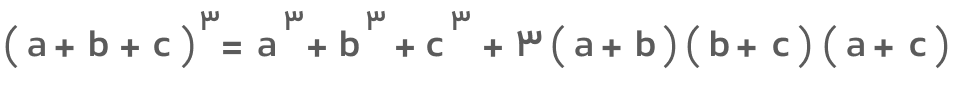
اثبات اتحاد مکعب سه جمله ای

برای اثبات اتحاد مکعب سه‌‌جمله‌‌ای کافی‌‌ست ابتدا این اتحاد را به‌‌شکل اتحاد مکعب دوجمله‌‌ای دربیاوریم:

اگر عبارت ( b + c ) را یک جمله در نظر بگیریم، می‌‌توانیم با استفاده از فرمول اتحاد مکعب دوجمله‌‌ای عبارت توان‌‌دار را باز کنیم. خواهیم داشت:

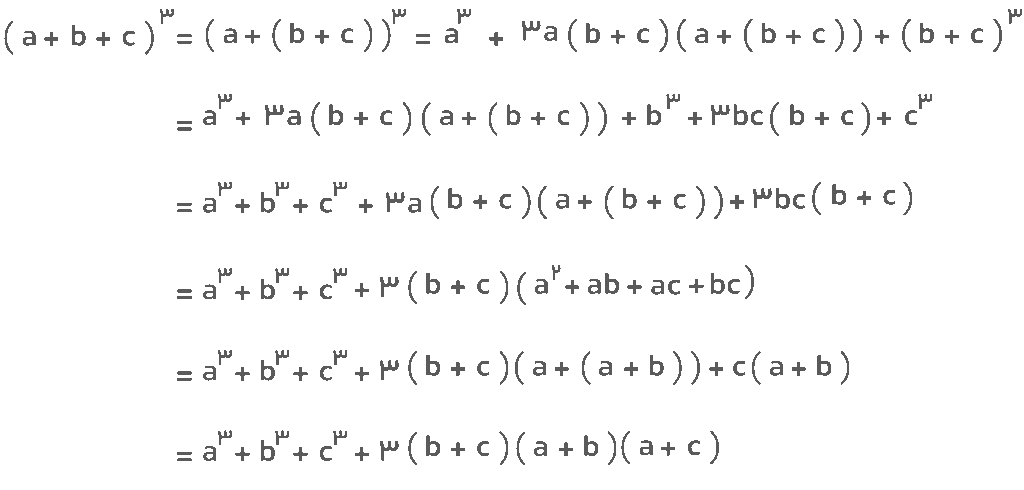
مثال هایی از اتحاد مکعب

با توجه به اینکه کاربرد اتحادها با حل مسائل متنوع مشخص می‌‌شود، در این بخش چند مثال در این رابطه حل می‌‌کنیم.

مثال اول: حاصل ۱۰۲^۳ را به دست آورید.

جواب: اگر بخواهیم عدد ۱۰۲ را به توان ۳ برسانیم، باید آن را ۳ بار در خودش ضرب کنیم که در این صورت انجام آن وقت‌‌گیر خواهد بود. با توجه به اینکه عدد ۱۰۲ به توان ۳ رسیده است، می‌‌توانیم از اتحاد مکعب مجموع دو جمله برای رسیدن به جواب نهایی استفاده کنیم. پس این عدد را به‌‌صورت زیر بسط می‌‌دهیم و فرمول اتحاد مکعب را به کار می‌‌بریم.

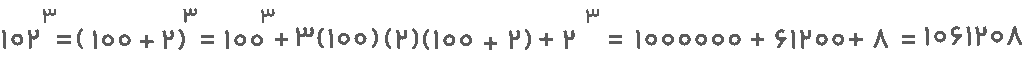
مثال دوم: عبارت ۳x-۵)^۳ ) را ساده کنید.
جواب: این عبارت تفاضل دو جمله را نشان می‌‌دهد که به توان ۳ رسیده است. پس از فرمول اتحاد مکعب تفاضل دو جمله کمک می‌‌گیریم. داریم:

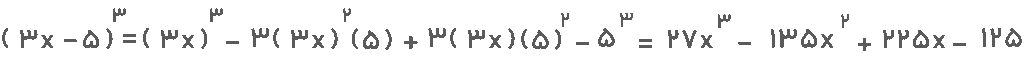
مثال سوم: حاصل عبارت زیر را تعیین کنید.

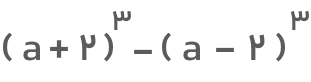
جواب: ابتدا هر دو اتحاد مکعب را بسط می‌‌دهیم:

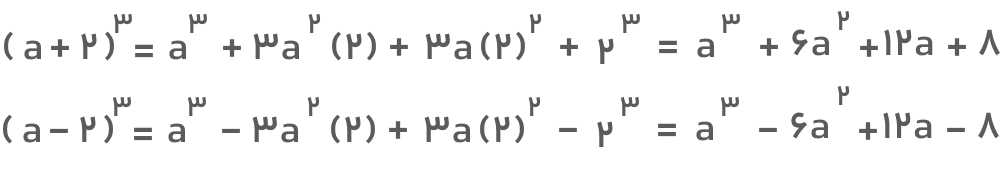
تفاضل این دو برابر است با:

اگر دقت کنید حاصل عبارت داده‌‌شده را با کمک اتحاد چاق و لاغر هم می‌‌توانید به دست آورید. به‌‌عنوان تمرین، حل آن را به عهده خودتان قرار می‌‌دهیم.

مثال چهارم: عبارت زیر را ساده کنید.

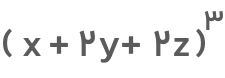
جواب: این عبارت همان اتحاد مکعب مجموع سه جمله است. براساس فرمول این اتحاد عبارت را ساده می‌‌کنیم. خواهیم داشت:

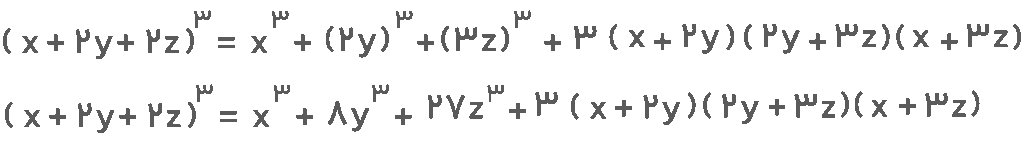
سخن پایانی

کاربرد اتحاد مکعب در حل مسائل جبری تنها به مسائلی که در اینجا حل کردیم محدود نمی‌‌شود و نمی‌‌توان تمام مسائل را در این آموزش گنجاند. ما سعی کردیم چند مثال ساده از این مبحث حل کنیم تا ذهن‌‌تان برای مسائل پیچیده‌‌تر آماده شود و بتوانید درک بهتری از آن‌‌ها داشته باشید. در انتها بهتر است این نکته را نیز بیان کنیم که اگر بتوانید اتحاد مکعب را از اتحاد چاق و لاغر تشخیص دهید و آن‌‌ها را در حافظه‌‌تان ثبت کنید، نصف راه را رفته‌‌اید و حل مسائل برایتان راحت‌‌تر خواهد بود.