فهرست مطالب
Toggleاگر یک شکل را ۱۸۰ درجه حول یک نقطه ثابت بچرخانیم، آیا آن شکل همچنان ظاهر اصلی خود را حفظ خواهد کرد؟ چگونه متوجه شویم یک شکل پس از دوران نیمدور نسبت به حالت اولیهاش متقارن است؟ برای دریافت پاسخ این سؤالها باید به بررسی تقارن مرکزی بپردازیم که در این مقاله، مفصل درمورد آن توضیح خواهیم داد و با حل چند مثال مختلف، تشخیص تقارن مرکزی در اشکال هندسی را برای شما راحتتر خواهیم کرد.
تقارن مرکزی چیست؟
اگر یک شکل را بهاندازه نیمدور (۱۸۰ درجه) حول نقطهای (مرکز) بچرخانیم، طوری که پس از چرخش، شکل روی خودش منطبق شود، میگوییم شکل تقارن مرکزی یا تقارن نقطهای دارد.
یک شکل را به دلخواه خود مانند شکل زیر روی یک کاغذ رسم کنید و یک نقطه ثابت را مانند نقطه قرمزرنگ در تصویر روی آن مشخص کنید.
حالا یک طلق شفاف روی شکل قرار دهید و الگوی شکل را روی آن بکشید. سپس، با مداد یا چیزی شبیه به آن طلق را در نقطه قرمزرنگ نگه دارید و مانند شکل زیر بهاندازه نیمدور (۱۸۰ درجه) طلق را حول نقطه ثابت قرمزرنگ بچرخانید.
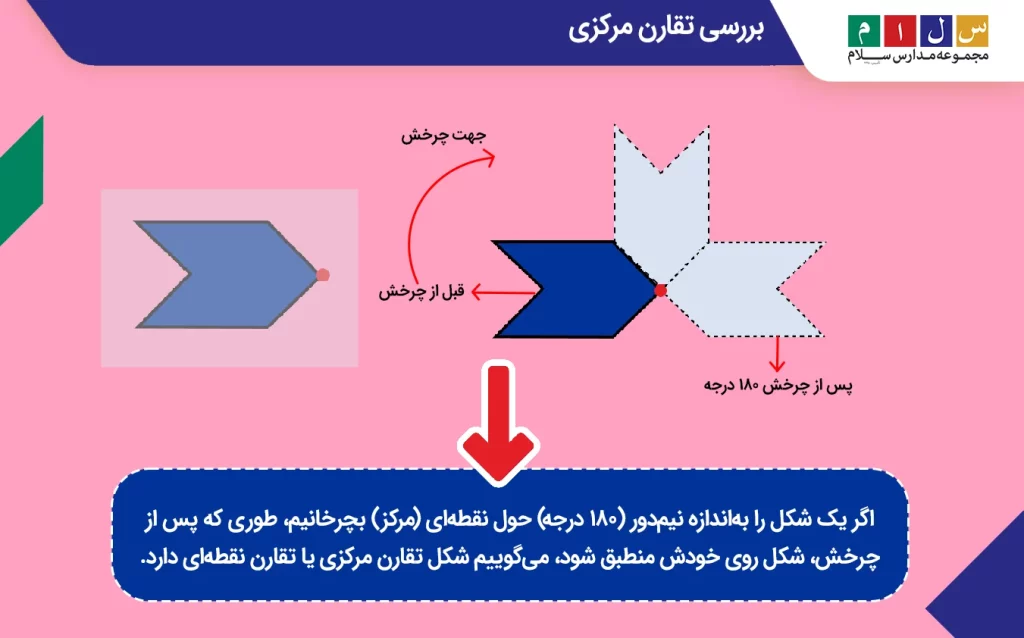
همانطور که میبینید، شکل قبل از دوران و شکل پس از دوران ۱۸۰ درجه، نسبت به نقطه ثابت قرمزرنگ قرینه یکدیگر هستند و فاصله نقاط مشابه هر دو شکل تا این نقطه با هم برابر است. این بدین معناست که دو شکل (قبل از دوران و پس از دوران ۱۸۰ درجه) نسبت به نقطه ثابت تقارن مرکزی دارند.
شکلهایی مانند مربع که در زاویه خاصی مانند ۹۰ درجه به حالت اولیه خود بر میگردند، علاوه بر تقارن مرکزی دارای یکی دیگر از انواع تقارن بهنام تقارن چرخشی نیز هستند.
نکته: فرقی نمیکند که دوران شکل در جهت حرکت عقربههای ساعت انجام شود یا خلاف جهت آن.
نقطهای که شکل را حول آن میچرخانیم و شکل موردنظر نسبت به آن تقارن مرکزی دارد را مرکز تقارن میگویند.
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
تقارن مرکزی یک شکل را چگونه تشخیص دهیم؟
برای اینکه مشخص کنیم آیا یک شکل تقارن مرکزی دارد یا خیر، از دو روش استفاده میکنیم:
روش اول: شکل را بهاندازه ۱۸۰ درجه دوران میدهیم. اگر شکل پس از چرخش مشابه و قرینه شکل اصلی بود و روی خودش منطبق شد، یعنی شکل موردنظر تقارن مرکزی دارد که میتوان آن را با خط تقارن نمایش داد.
روش دوم: نقاط مختلفی از شکل را درنظر میگیریم و از آن نقاط تا مرکز یک خط رسم میکنیم. سپس، خط را بههمان اندازه تا مرکز امتداد میدهیم. اگر همان نقاط از شکل در طرف مقابل با همان فاصله از مرکز وجود داشت، یعنی شکل تقارن مرکزی دارد.
برای مثال، در شکل زیر، فاصله هر دو نقطه همرنگ تا مرکز با هم برابر است. این نشان میدهد که شکل زیر تقارن مرکزی دارد. همچنین، اگر مانند روش اول، شکل را حول مبدأ ۱۸۰ درجه دوران دهیم، شکل روی خودش منطبق میشود.
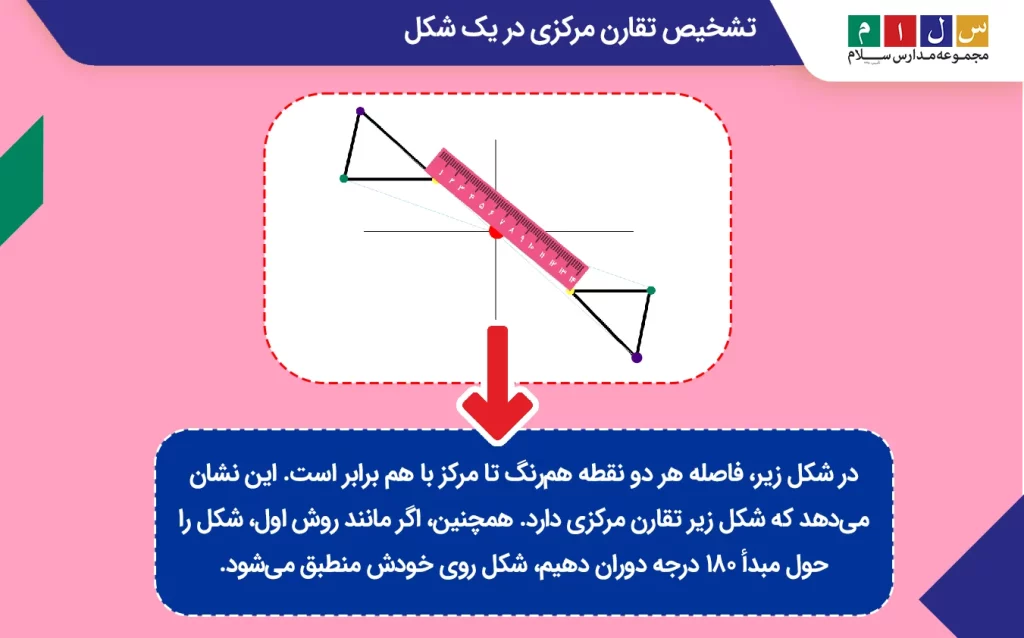
تفاوت تقارن مرکزی و مرکز تقارن چیست؟
شباهت دو عبارت تقارن مرکزی و مرکز تقارن باعث میشود که برخی از دانشآموزان این دو را با هم اشتباه بگیرند. بنابراین، در این بخش تفاوت آنها را بیان میکنیم تا این اشتباه به حداقل برسد.
تقارن مرکزی یعنی منطبق شدن یک شکل روی خودش پس از دوران ۱۸۰ درجه حول یک نقطه ثابت، اما مرکز تقارن یعنی نقطه ثابتی که دوران ۱۸۰ درجه را حول آن انجام میدهیم.
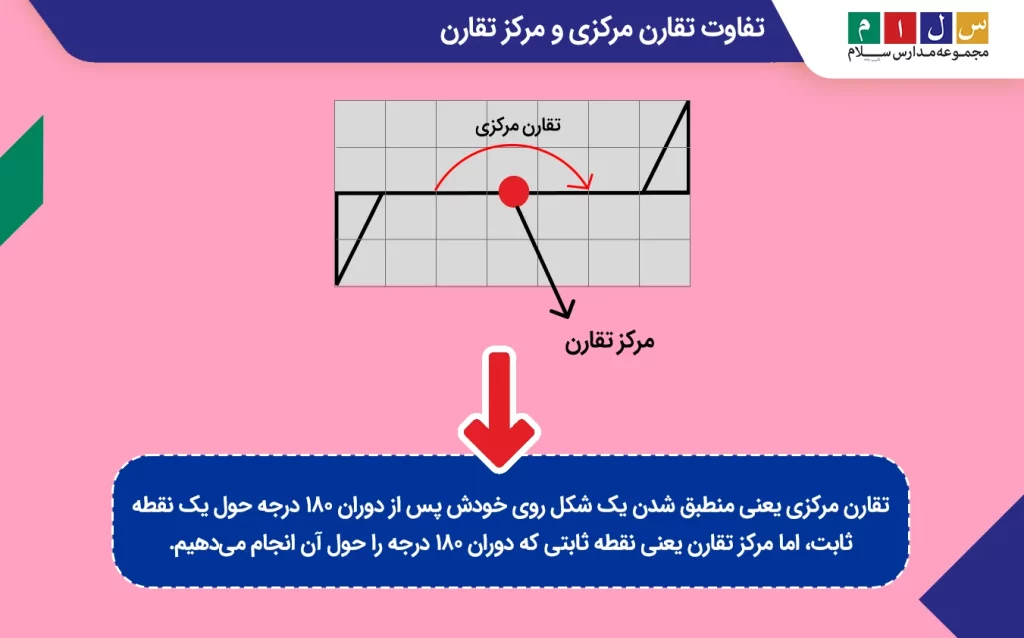
آیا دایره تقارن مرکزی دارد؟
بله، دایره یک شکل متقارن است و مرکز دایره، مرکز تقارن آن محسوب میشود. یعنی اگر دایره را حول مرکز خودش ۱۸۰ درجه (یا هر زاویهای) بچرخانیم، شکل دقیقاً روی خودش منطبق میشود. این ویژگی نشان میدهد که دایره بینهایت محور تقارن و یک مرکز تقارن دارد.
آیا متوازیالاضلاع مرکز تقارن دارد؟
بله، محل تقاطع دو قطر متوازیالاضلاع مرکز تقارن آن است.
اگر متوازیالاضلاع را روی کاغذ رسم کنیم و شکل را حول نقطهی تقاطع قطرها به اندازه ۱۸۰ درجه بچرخانیم، میبینیم که شکل روی خودش منطبق میشود.
این یعنی هر نقطه از شکل، در طرف مقابل مرکز تقارن، نقطهی متناظری دارد که فاصلهاش از مرکز دقیقاً برابر است.
آیا مستطیل تقارن مرکزی دارد؟
مستطیل و مربع شکلهایی هستند که تقارن مرکزی دارند.
مرکز تقارن مستطیل نقطهای است که قطرها همدیگر را قطع میکنند. اگر مستطیل را حول آن نقطه ۱۸۰ درجه دوران دهیم، شکل دقیقاً روی خودش قرار میگیرد. به همین دلیل میگوییم مستطیل و مربع هر دو دارای تقارن مرکزی هستند.
آیا مثلث تقارن مرکزی دارد؟
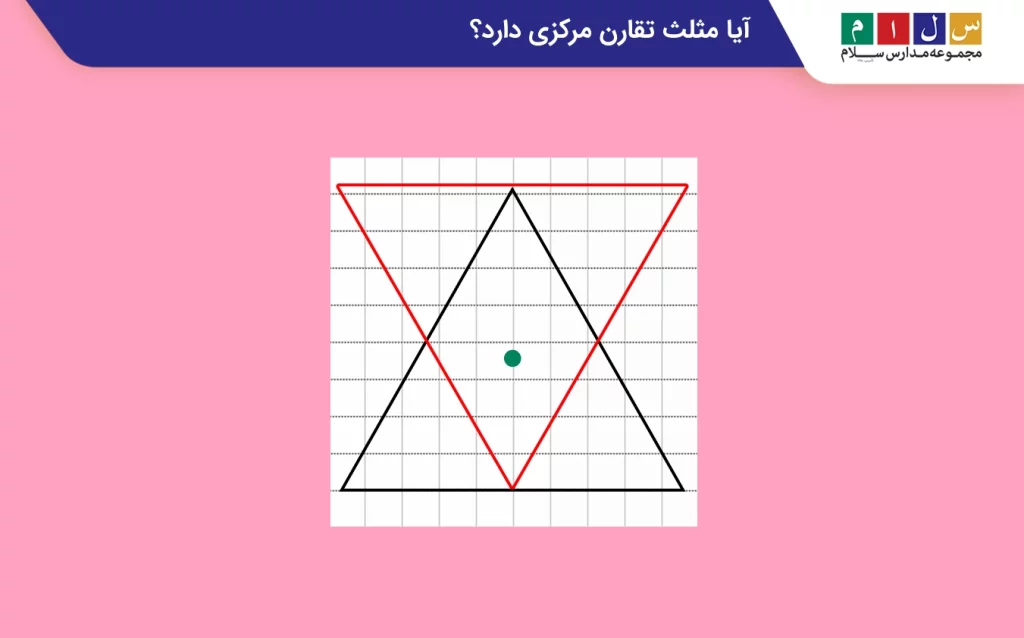
برای بررسی این موضوع، ابتدا مثلثی را رسم میکنیم و نقطهای مانند مرکز احتمالی تقارن را در نظر میگیریم.
اگر مثلث را ۱۸۰ درجه حول آن نقطه بچرخانیم، متوجه میشویم که شکل حاصل (مثلث قرمز) روی مثلث اولیه (مثلث سیاه) منطبق نمیشود.
پس نتیجه میگیریم که مثلث هیچ مرکز تقارنی ندارد.
تفاوت تقارن مرکزی و تقارن چرخشی چیست؟
تقارن چرخشی یعنی منطبق شدن یک شکل روی خودش پس از دوران ۱۸۰ درجه یا کمتر از ۱۸۰ درجه حول یک نقطه ثابت، اما تقارن مرکزی یعنی منطبق شدن شکل روی خودش پس از دوران ۱۸۰ درجه حول یک نقطه ثابت.
این دو تعریف نشان میدهد که تقارن مرکزی نوعی تقارن چرخشی است. بهعبارت دیگر، میتوان گفت اگر شکلی تقارن مرکزی داشته باشد، تقارن چرخشی نیز دارد، اما برعکس آن همیشه ممکن نیست، یعنی اگر شکلی دارای تقارن چرخشی باشد، ممکن است تقارن مرکزی نداشته باشد.
پیشنهاد مطالعه: تقارن محوری چیست؟
مثال هایی از تقارن مرکزی ریاضی ششم
در این بخش، به حل چند مثال از تقارن مرکزی میپردازیم تا بهتر بتوانید این نوع تقارن را در اشکال مختلف تشخیص دهید.
مثال ۱: آیا شکل زیر حول مبدأ تقارن مرکزی دارد؟
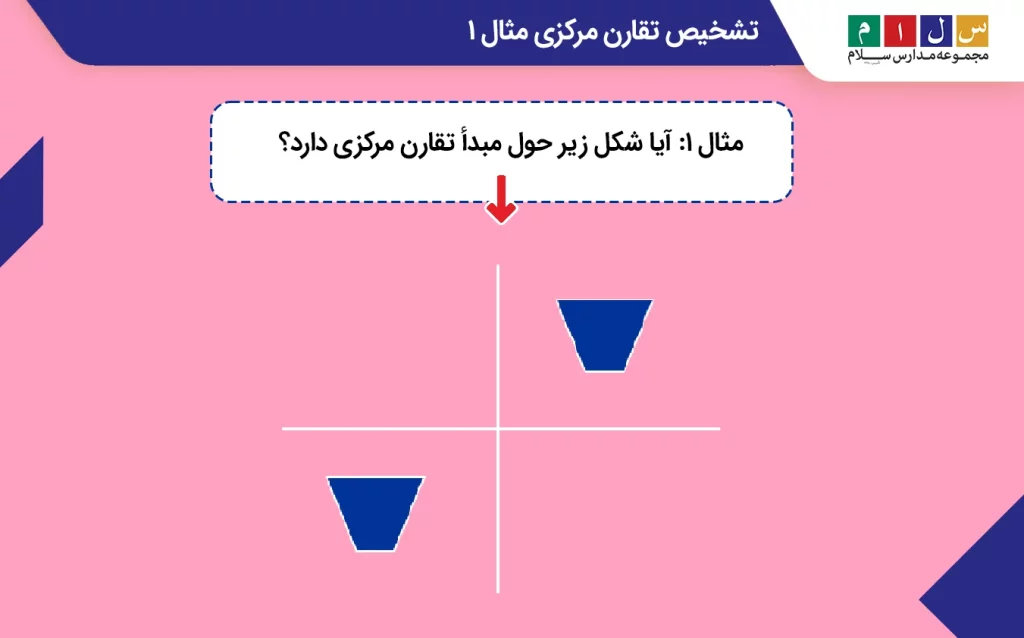
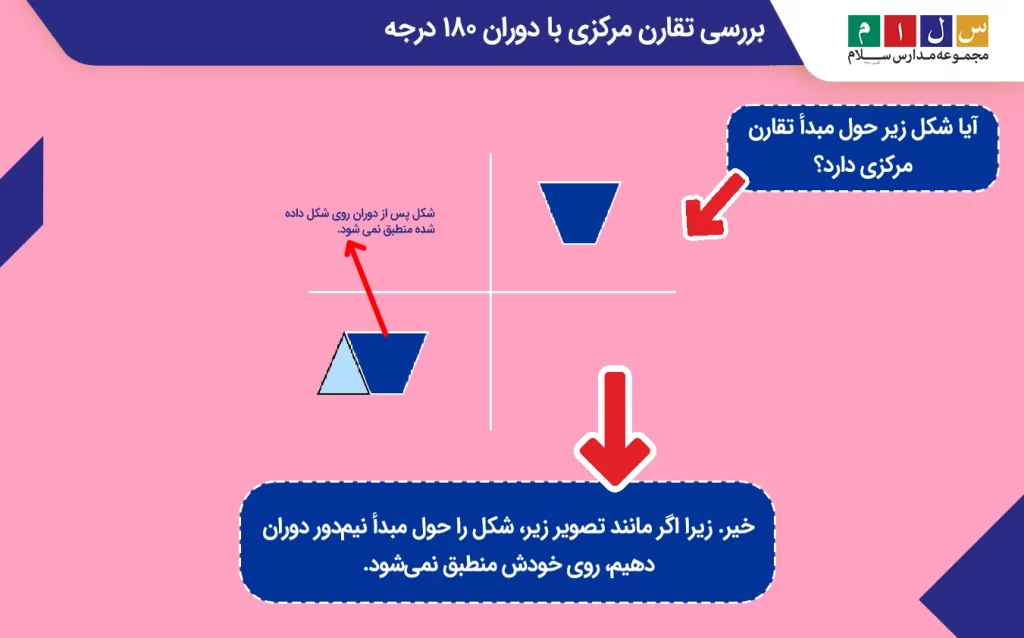
جواب: خیر. زیرا اگر مانند تصویر زیر، شکل را حول مبدأ نیمدور دوران دهیم، روی خودش منطبق نمیشود.
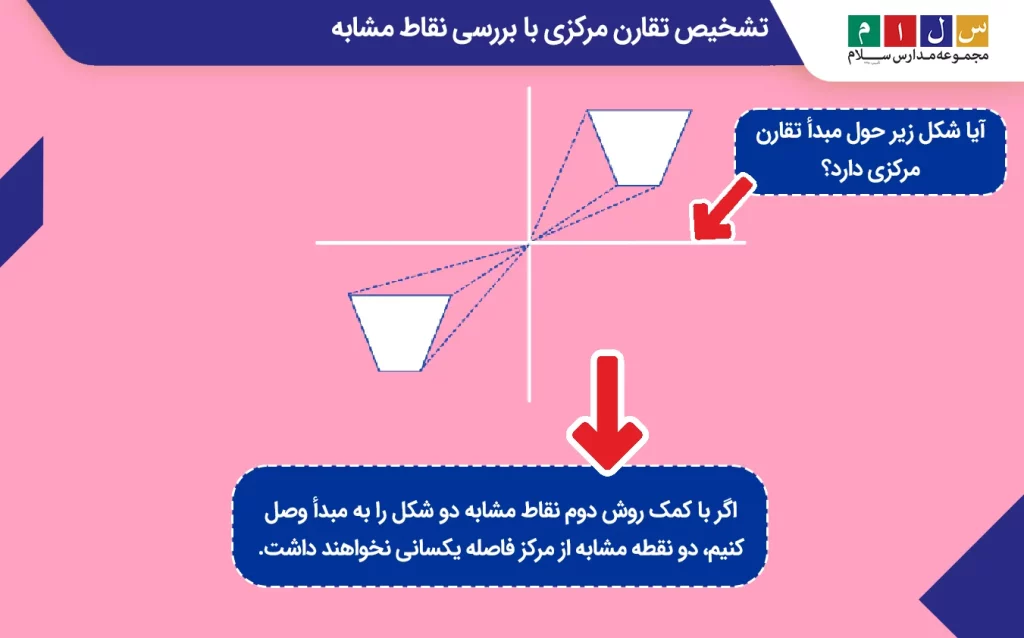
علاوهبراین، اگر با کمک روش دوم نقاط مشابه دو شکل را به مبدأ وصل کنیم، دو نقطه مشابه از مرکز فاصله یکسانی نخواهند داشت.
مثال ۲: تقارن مرکزی شکل زیر را بررسی کنید.
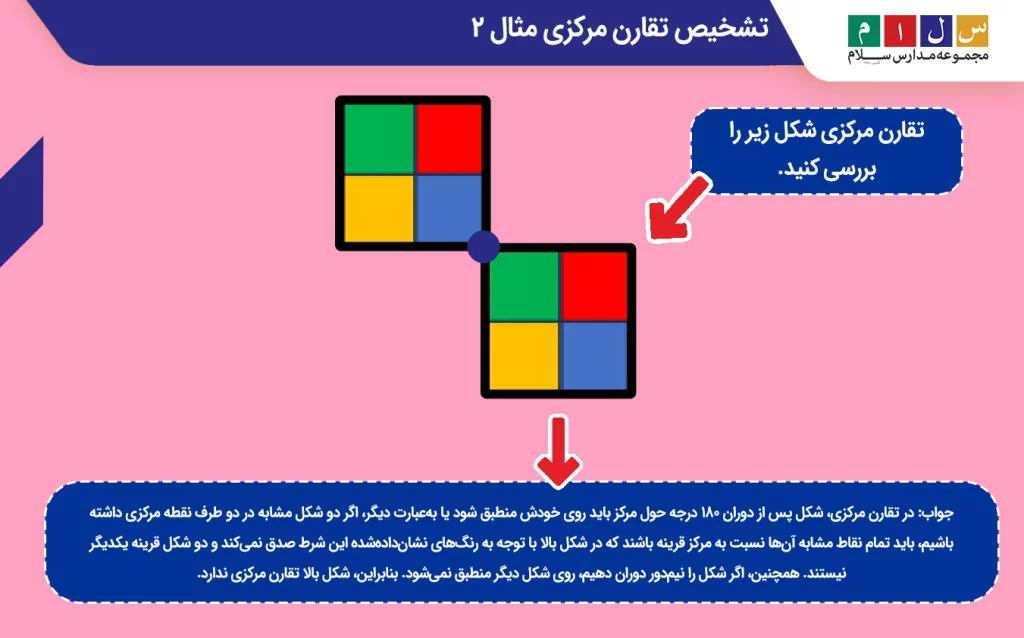
جواب: در تقارن مرکزی، شکل پس از دوران ۱۸۰ درجه حول مرکز باید روی خودش منطبق شود یا بهعبارت دیگر، اگر دو شکل مشابه در دو طرف نقطه مرکزی داشته باشیم، باید تمام نقاط مشابه آنها نسبت به مرکز قرینه باشند که در شکل بالا با توجه به رنگهای نشاندادهشده این شرط صدق نمیکند و دو شکل قرینه یکدیگر نیستند. همچنین، اگر شکل را نیمدور دوران دهیم، روی شکل دیگر منطبق نمیشود. بنابراین، شکل بالا تقارن مرکزی ندارد.
مثال ۳: آیا شکل زیر مرکز تقارن دارد؟
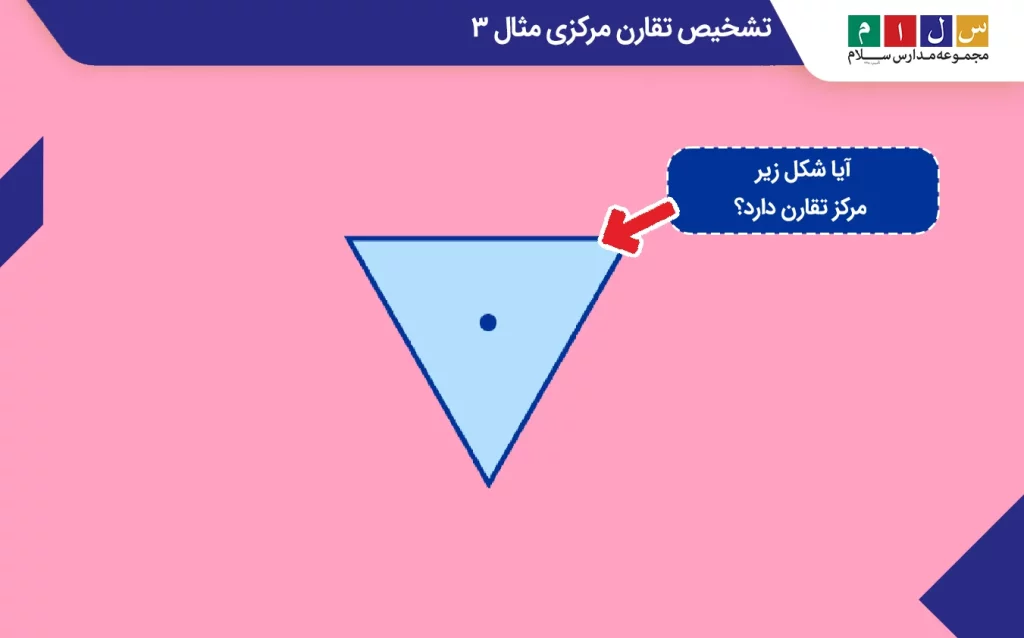
جواب: برای اینکه مشخص کنیم شکل فوق تقارن مرکزی دارد یا نه، آن را مانند تصویر زیر بهاندازه ۱۸۰ درجه حول مرکزش دوران میدهیم.
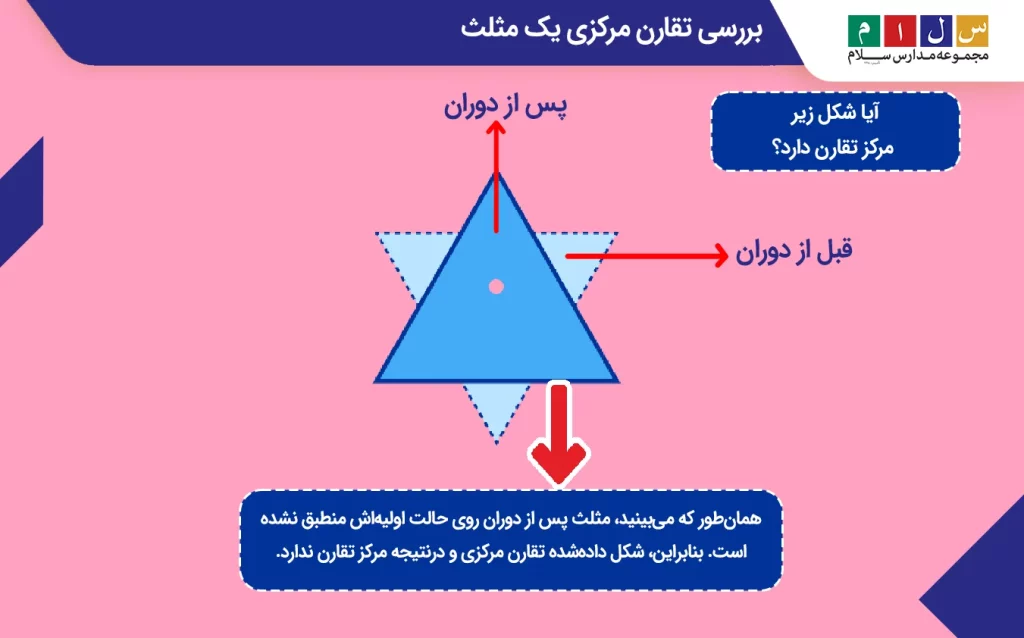
همانطور که میبینید، مثلث پس از دوران روی حالت اولیهاش منطبق نشده است. بنابراین، شکل دادهشده تقارن مرکزی و درنتیجه مرکز تقارن ندارد.
مثال ۴: آیا تابلوی ورود ممنوع تقارن مرکزی دارد؟
جواب: تابلوی ورود ممنوع بهشکل زیر است:

اگر این تابلو را حول مرکزش بهاندازه نیمدور بچرخانیم، روی خودش منطبق میشود. بنابراین، تابلوی ورود ممنوع تقارن مرکزی و مرکز تقارن دارد.

مثال هایی از تقارن مرکزی
در این بخش، به بررسی تقارن مرکزی چند شکل مختلف میپردازیم.
مثال ۱: با ذکر دلیل بررسی کنید که آیا شکل زیر تقارن مرکزی دارد یا خیر.

جواب: برای اینکه بفهمیم شکل بالا تقارن مرکزی دارد یا نه، از چند نقطه مختلف تا مرکز یک خط رسم میکنیم و بههمان اندازه تا نقطه مشابه در شکل دیگر امتداد میدهیم. همانطور که در شکل زیر میبینید، فاصله خطوط رسمشده تا مرکز برای دو نقطه مشابه در شکل یکسان است. بنابراین، شکل بالا تقارن مرکزی دارد.
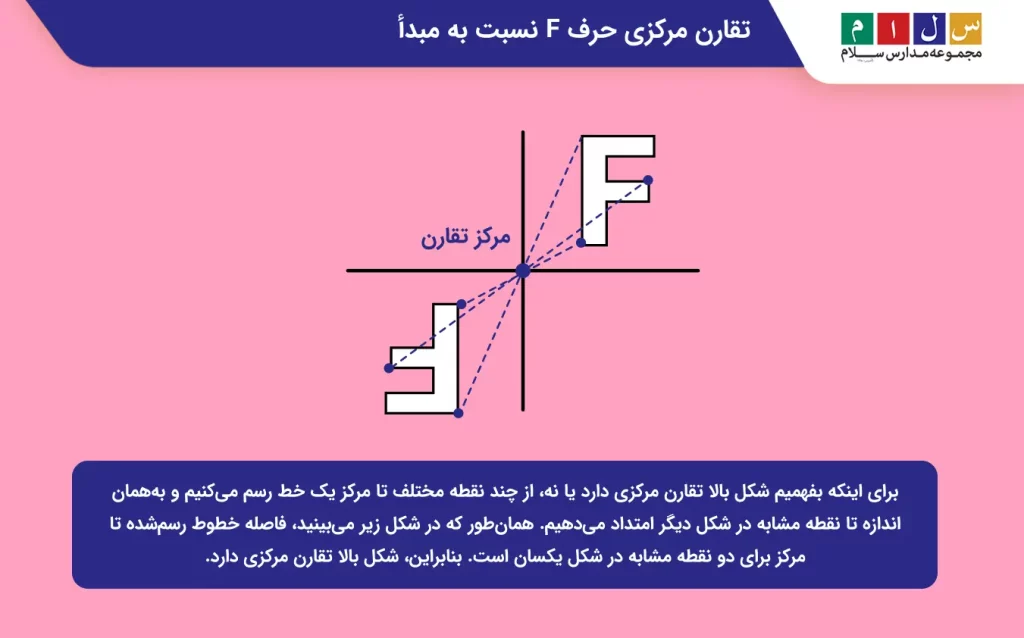
مثال ۲: تقارن مرکزی شکل زیر را بررسی کنید.

جواب: اگر از هر کدام از رأسهای ستاره تا مرکز یک خط رسم کنیم و آن را بههمان اندازه امتداد دهیم به نقطه مشابه در شکل روبهرو میرسیم. پس طبق تصویر زیر، شکل موردنظر تقارن مرکزی دارد.
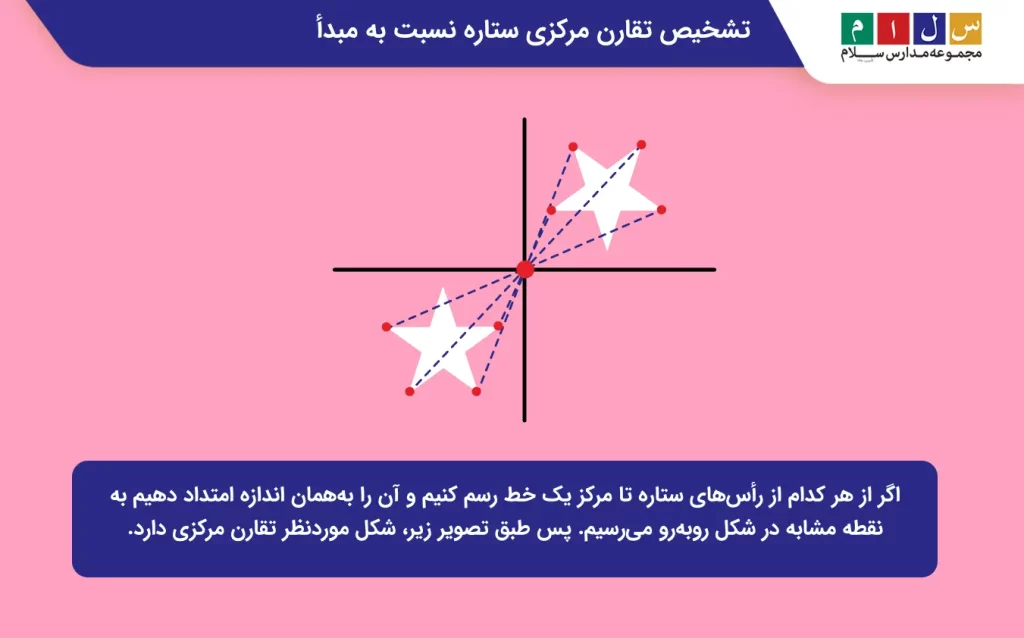
مثال ۳: آیا شکل زیر تقارن مرکزی دارد؟

جواب: همانطور که در تصویر زیر میبینید، اگر شکل را نیمدور بچرخانیم و از دو نقطه مشابه تا مرکز یک خط رسم کنیم، فاصله نقاط از مرکز با هم برابر نیست. بنابراین، این شکل نسبت به مرکز متقارن نیست.
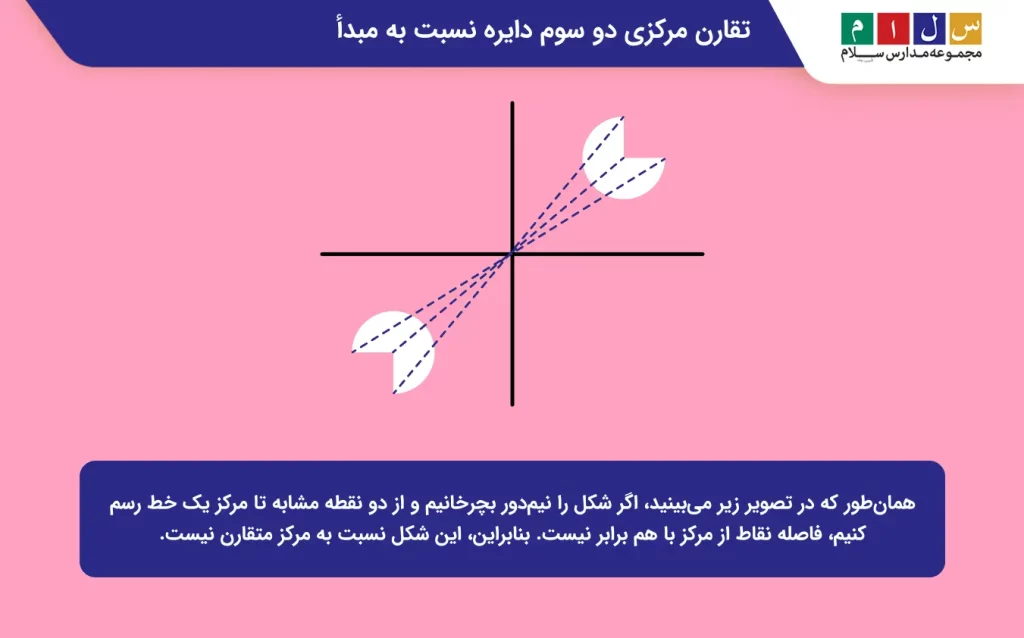
مثال ۴: آیا شکل زیر دارای تقارن مرکزی است؟ دلیل بیاورید.

جواب: خیر. چون فاصله نقاط مشابه در دو شکل تا مرکز یکسان نیست. علاوهبراین، اگر شکل را ۱۸۰ درجه بچرخانید، متوجه خواهید شد که رنگهای دو شکل قرینه و بازتاب یکدیگر نیستند.
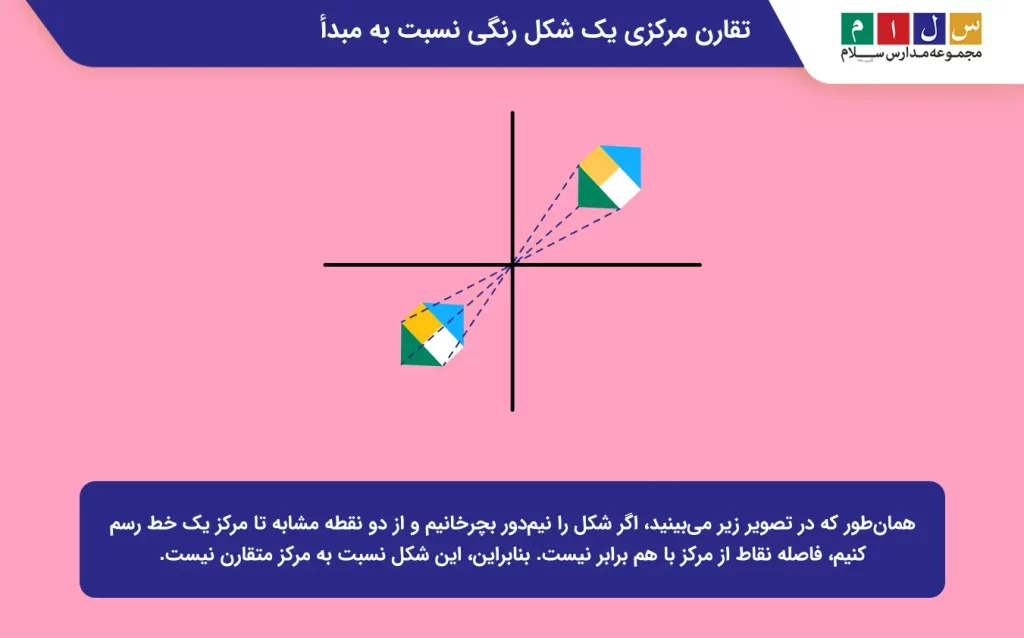
مثال ۵: تقارن مرکزی حروف انگلیسی N، O و Z را مشخص کنید.
جواب: ابتدا مرکز این حروف را مشخص کرده. سپس، نقاط قرینه و مشابه را به مرکز وصل میکنیم. همانطور که در تصویر زیر نشان داده شده است، در هر سه حروف فاصله خطوط رسمشده تا مرکز برای دو نقطه مشابه یکسان است. بنابراین، میتوان نتیجه گرفت که این حروف تقارن مرکزی و درنتیجه مرکز تقارن دارند. بهعبارت دیگر، اگر هر یک از حروف را حول نقطه o (مرکز تقارن) بهاندازه ۱۸۰ درجه بچرخانیم، روی خودشان منطبق میشوند.
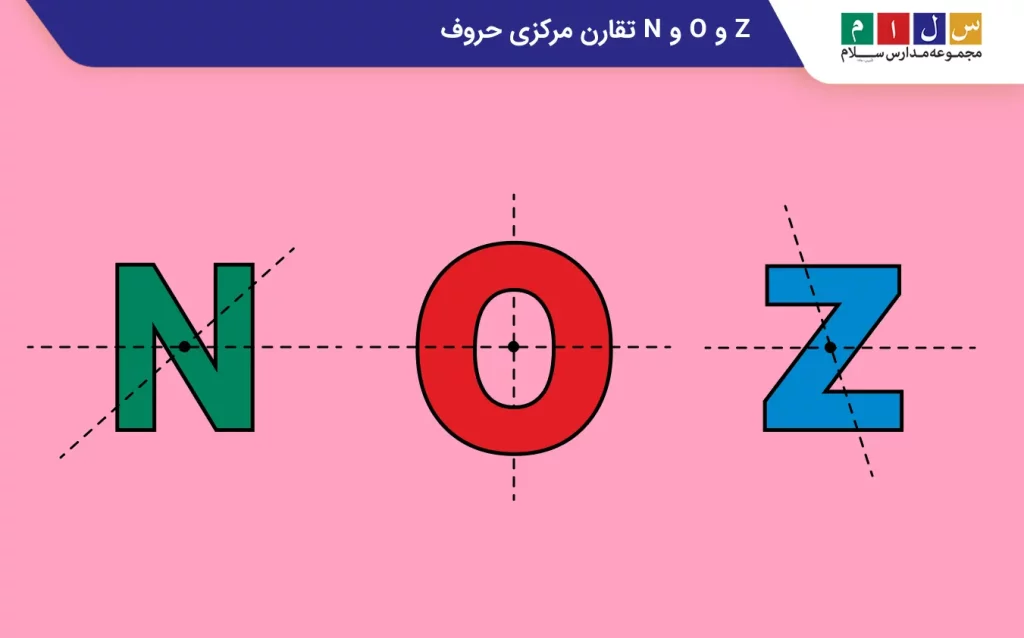
تقارن مرکزی اشکال هندسی مختلف
در این قسمت، تقارن مرکزی و مرکز تقارن اشکال هندسی را بررسی کرده و آنها را در قالب یک جدول آوردهایم. توجه داشته باشید هر کدام از اشکال هندسی که تقارن مرکزی دارند، دارای مرکز تقارن هم هستند.
| شکل | تقارن مرکزی |
| دارد | |
| ندارد | |
| ندارد | |
| دارد | |
| دارد | |
| دارد | |
| دارد | |
| دارد | |
| انواع مثلث | ندارد |
| انواع ذوزنقه | ندارد |
| فردضلعیهای منتظم | ندارند |
| زوجضلعیهای منتظم | دارند |
سخن پایانی
اگر یک شکل را بهاندازه نیمدور (۱۸۰ درجه) حول نقطهای ثابت دوران دهیم، طوری که پس از دوران، شکل روی خودش منطبق شود، میگوییم شکل تقارن مرکزی یا تقارن نقطهای دارد. نقطهای که شکل را حول آن دوران میدهیم و شکل موردنظر نسبت به آن تقارن مرکزی دارد را مرکز تقارن میگوییم. در تقارن مرکزی فرقی نمیکند که جهت چرخش در جهت حرکت عقربههای ساعت باشد یا خلاف آن. بسیاری از اشکال هندسی نسبت به مرکزشان تقارن مرکزی دارند، ازجمله دایره، بیضی، مربع، لوزی، مستطیل، متوازیالاضلاع و زوجضلعیهای منتظم.
سؤالات متداول
- تقارن مرکزی چیست؟
نوعی تقارن است که در آن شکل پس از چرخش بهاندازه ۱۸۰ درجه حول یک نقطه ثابت، به حالت اولیه خود بازمیگردد. - مرکز تقارن یعنی چه؟
نقطهای که شکل را حول آن میچرخانیم و شکل موردنظر نسبت به آن تقارن مرکزی دارد را مرکز تقارن میگویند. - چه شکلهایی تقارن مرکزی دارند؟
اشکالی تقارن مرکزی دارند که پس از نیمدور چرخش حول یک نقطه ثابت روی خودشان منطبق شوند. - چگونه تقارن مرکزی را در یک شکل تشخیص دهیم؟
از دو روش میتوانیم تقارن مرکزی را تشخیص دهیم:
روش اول: شکل را نیمدور دوران دهیم. اگر شکل پس از دوران روی خودش منطبق شد یعنی تقارن مرکزی دارد.
کدام یک از اشکال هندسی، دارای تقارن مرکزی هستند؟
روش دوم: نقاطی از شکل را درنظر میگیریم و با رسم یک خط آنها را به مرکز وصل میکنیم. سپس بههمان اندازه خط را امتداد میدهیم. اگر قرینه این نقاط مشابه را در طرف مقابل با همان فاصله از مرکز یافتیم، شکل موردنظر تقارن مرکزی خواهد داشت. - کدام یک از اشکال هندسی، دارای تقارن مرکزی هستند؟
دایره، بیضی، مربع، لوزی، مستطیل، متوازیالاضلاع و زوجضلعیهای منتظم ازجمله اشکال هندسی هستند که تقارن مرکزی و مرکز تقارن دارند.









