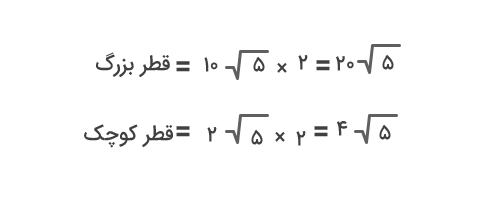فهرست مطالب
Toggleبیضی یک شکل بسته است که مجموع فاصله تمام نقاط روی آن از دو نقطه ثابت درون بیضی بهنام کانون یکسان است. اندازه سطح داخل این شکل هندسی مانند سایر اشکال هندسی دوبعدی قابل محاسبه است و میتوان مقدار مساحت آن را بهدست آورد. در این مقاله، با معرفی فرمول مساحت بیضی، روش محاسبه آن را با حل مثال آموزش میدهیم.
مساحت بیضی چیست؟
بیضی یکی از انواع اشکال هندسی است و مجموعه نقاطی از یک صفحه است که مجموع فاصله آنها از دو نقطه ثابت بهنام کانون یکسان و ثابت است.
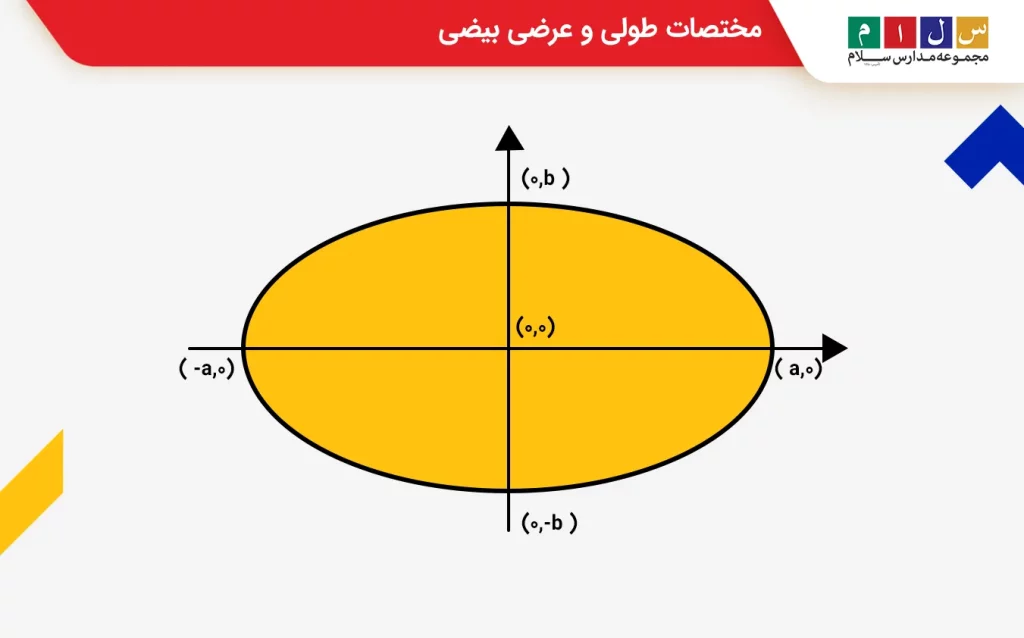
مساحت بیضی برابر است با اندازه سطح داخل آن. در شکل زیر، سطح احاطهشده توسط منحنی قرمزرنگ (سطح داخلی بیضی) مساحت این شکل هندسی را نشان میدهد.

پیشنهاد مطالعه: مساحت چیست؟
اولین نفری باشید که از اخبار و اطلاعیههای مرتبط با پایه تحصیلیتان باخبر میشود!
مساحت بیضی چگونه بدست می آید؟
برای محاسبه مساحت بیضی باید مقدار طول محورهای اصلی و فرعی آن را بدانیم. محور اصلی بیضی را قطر بزرگ و محور فرعی آن را قطر کوچک میگویند. این محورها بر هم عمودند و هر دو از مرکز بیضی عبور میکنند. اگر به خاطر داشته باشید، برای محاسبه مساحت دایره به اندازه قطر و شعاع آن نیاز داشتیم. در اینجا نیز برای بهدست آوردن مساحت بیضی از قطر و شعاع بیضی استفاده میکنیم. البته چون بیضی قطرهایی با اندازههای متفاوت دارد، باید هر دو قطر بزرگ وکوچک آن را در نظر بگیریم.
شعاع بزرگ بیضی برابر با نصف قطر بزرگ و شعاع کوچک آن مساوی با نصف قطر کوچک است. بهطور کلی، مساحت بیضی از فرمول زیر بهدست میآید:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
اگر بخواهیم این فرمول را برحسب نمادهای ریاضی و بهصورت جبری بنویسیم، فرمول مساحت بیضی بهشکل زیر خواهد بود:
A=πab
- a: شعاع بزرگ بیضی
- b: شعاع کوچک بیضی
- π: عدد پی (۳/۱۴)
- A: مساحت بیضی

پیشنهاد مطالعه: قطر چیست؟
اثبات فرمول مساحت بیضی با استفاده از معادله دایره
برای اثبات فرمول مساحت بیضی میتوانیم از معادله دایره و فرمول مساحت آن کمک بگیریم. ابتدا از معادله بیضی شروع میکنیم و آن را بهصورت زیر مینویسیم:
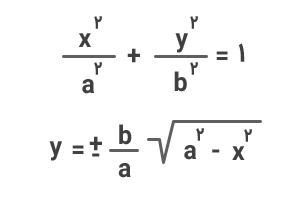
اکنون معادله دایرهای به شعاع a را که مرکز آن در مبدأ مختصات قرار دارد به همین صورت بازنویسی میکنیم:
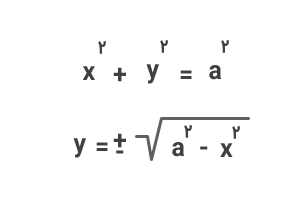
روابط بهدستآمده برای y در معادله دایره و بیضی نشان میدهد که مختصات بیضی مختصات دایره است. بنابراین، مساحت بیضی نیز
مساحت دایره است.

با توجه به اینکه مساحت دایرهای به شعاع a برابر با πa۲ است، مساحت بیضی را میتوانیم بهصورت زیر بهدست آوریم:
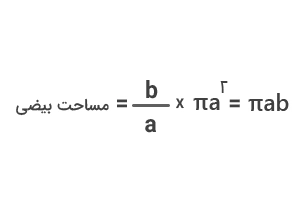
پیشنهاد مطالعه: محیط بیضی + ۹ فرمول کاربردی محیط بیضی
اثبات مساحت بیضی با انتگرال
روش دیگر برای بهدست آوردن فرمول مساحت بیضی استفاده از انتگرال است. میدانیم که معادله بیضی بهصورت زیر است:
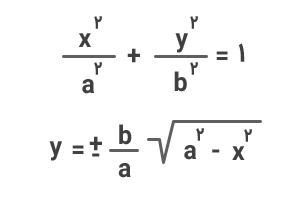
محورهای اصلی و فرعی، بیضی را به چهار قسمت مساوی تقسیم میکنند. با توجه به اینکه طول منحنی بیضی و اندازه سطح زیر آن در هر چهار ربع با هم برابر است، کافیست مساحت ربع اول را محاسبه کرده و سپس، حاصل آن را در ۴ ضرب کنیم. طبق شکل زیر، بازه متغیر x در ربع اول ۰ تا a است. بنابراین، مساحت بیضی را میتوان از انتگرال زیر محاسبه کرد:
با جایگذاری مقدار y در فرمول بالا داریم:
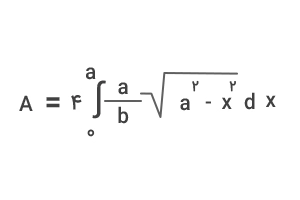
ازآنجا که در ربع اول مقدار y مثبت است، در اینجا مقدار مثبت آن را در نظر گرفتیم. با تغییر متغیرهای x و dx بهصورت زیر میتوانیم انتگرال را بهراحتی حل کنیم.
x = a sin sin t
dx = a cos cos t dt
با تغییر متغیرها بازه انتگرال نیز به ۰ تا تغییر مییابد. درنتیجه خواهیم داشت:

اکنون از a فاکتور میگیریم و انتگرال را حل میکنیم:
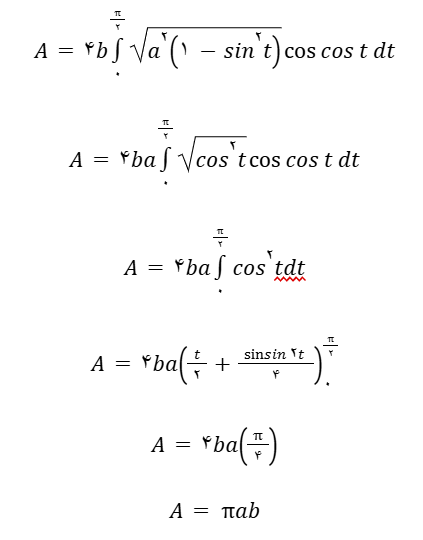
همانطور که میبینید، فرمول بهدستآمده دقیقاً همان فرمولی است که در ابتدا معرفی کردیم.
پیشنهاد مطالعه: مساحت دایره چیست؟
نمونه سؤال مساحت بیضی
در این قسمت، برای درک بهتر و یادگیری بیشتر مبحث مساحت بیضی به حل چند نمونه سؤال میپردازیم.
محاسبه مساحت بیضی با قطر
مساحت شکل زیر را بهدست آورید.

محورهای اصلی و فرعی بیضی دادهشده بهترتیب برابر با ۲۰ و ۱۰ سانتیمتر است. برای محاسبه مساحت بیضی باید طول این محورها را تقسیم بر دو کنیم تا مقدار شعاع بزرگ و کوچک بهدست آید:
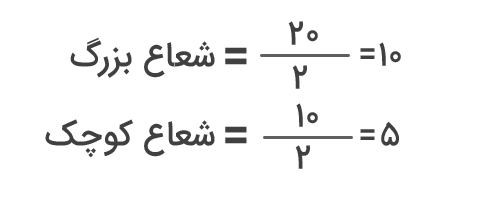
اکنون اندازه شعاعها را در فرمول مساحت بیضی قرار میدهیم تا مقدار مساحت تعیین شود:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
۱۵۷ = ۵ × ۱۰ × ۳/۱۴ = مساحت بیضی
بنابراین، مساحت بیضی برابر با ۱۵۷ سانتیمتر مربع است.
مساحت بیضی داخل مربع
در شکل زیر، یک بیضی توسط مربعی به ضلع ۱۱ سانتیمتر احاطه شده است. مساحت بیضی را محاسبه کنید.

در شکل بالا محیط بیضی روی اضلاع مربع مماس شده است. بنابراین، اندازه قطرهای بیضی برابر با اندازه اضلاع مربع یعنی ۱۱ سانتیمتر و درنتیجه شعاعهای آن مساوی ۵/۵ سانتیمتر خواهد بود. مساوی بودن شعاعها نشان میدهد که بیضی محاطی یک دایره است. دایره نوعی بیضی است که شعاعهای آن با هم برابرند. ازاینرو، مساحت بیضی داخل مربع بهصورت زیر محاسبه میشود:
شعاع کوچک × شعاع بزرگ × عدد پی = مساحت بیضی
۹۴/۹۸۵ = ۵/۵ × ۵/۵ × ۳/۱۴ = مساحت بیضی

بنابراین، مساحت بیضی محاطی مساوی با ۹۴/۹۸۵ سانتیمتر مربع است.
محاسبه قطرهای بیضی
مساحت یک بیضی ۳۱۴ سانتیمتر مربع است. اگر شعاع بزرگ ۵ برابر شعاع کوچک باشد، اندازه قطرهای بیضی چقدر است؟
اگر شعاع بزرگ را با a و شعاع کوچک را با b نشان دهیم، رابطه بین شعاعها بهصورت زیر خواهد بود:
a = ۵ b
با استفاده از فرمول مساحت بیضی مقدار شعاعها را تعیین میکنیم. داریم:
A = π a b
A = π ( ۵×b) b
۳۱۴ = ۳/۱۴ × ۵ × b۲
۳۱۴ =۱۵/۷ × b۲
b۲= ۳۱۴ ÷ ۱۵/۷ = ۲۰
b = √۲۰ =۲√۵
شعاع کوچک بیضی مساوی با ۲۵ سانتیمتر است. درنتیجه شعاع بزرگ برابر است با
a = ۵b = ۵ × ۲√ ۵ = ۱۰√۵
اندازه قطرهای بیضی دو برابر شعاعهای آن است. بنابراین، برای تعیین قطرهای بیضی کافیست اندازه شعاعها را در ۲ ضرب کنیم:
درنتیجه قطر بزرگ برابر با ۵√ ۲۰ سانتیمتر و قطر کوچک برابر با ۵√۴ سانتیمتر است.
سخن پایانی
در این آموزش توضیح دادیم که مساحت بیضی چیست و مقدار آن چگونه بهدست میآید. مساحت بیضی، اندازه سطح داخلی آن است که مقدار آن از حاصلضرب عدد پی در شعاع بزرگ در شعاع کوچک محاسبه میشود. شعاع کوچک نصف قطر کوچک و شعاع بزرگ نصف قطر بزرگ بیضی است. بهاینترتیب برای محاسبه مساحت بیضی به اندازه شعاعها یا قطرهای آن نیاز داریم. پیشنهاد میکنیم پس از یادگیری این مبحث نمونه سؤالهای بیشتری در این رابطه حل کنید تا مطالب بهخوبی در ذهنتان تثبیت شود.
سؤالات متداول
- مساحت بیضی چیست؟
مساحت بیضی برابر با اندازه سطح داخل محیط آن است. - مساحت بیضی چگونه بدست می آید؟
مساحتت بیضی از رابطه «عدد پی ضربدر شعاع بزرگ ضربدر شعاع کوچک» تعیین میشود. - فرمول جبری مساحت بیضی چیست؟
اگر شعاع بزرگ بیضی را با a و شعاع کوچک آن را با b نشان دهیم، شکل جبری فرمول مساحت بیضی بهصورت A=πab خواهد بود. - تفاوت فرمول مساحت بیضی و فرمول مساحت دایره چیست؟
دایره نوعی بیضی است که شعاع بزرگ و کوچک آن با هم برابرند. بنابراین، تفاوت فرمول مساحت این دو شکل هندسی در اندازه شعاعهای آنهاست.